Đề thi giữa HK2 Toán 11 năm 2018 – 2019 trường Newton – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ KIỂM TRA GIỮA KỲ 2 LỚP 11 TRƯỜNG THCS THP T NEWTON
NĂM HỌC 2018 – 2019 Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (5 ĐIỂM)        
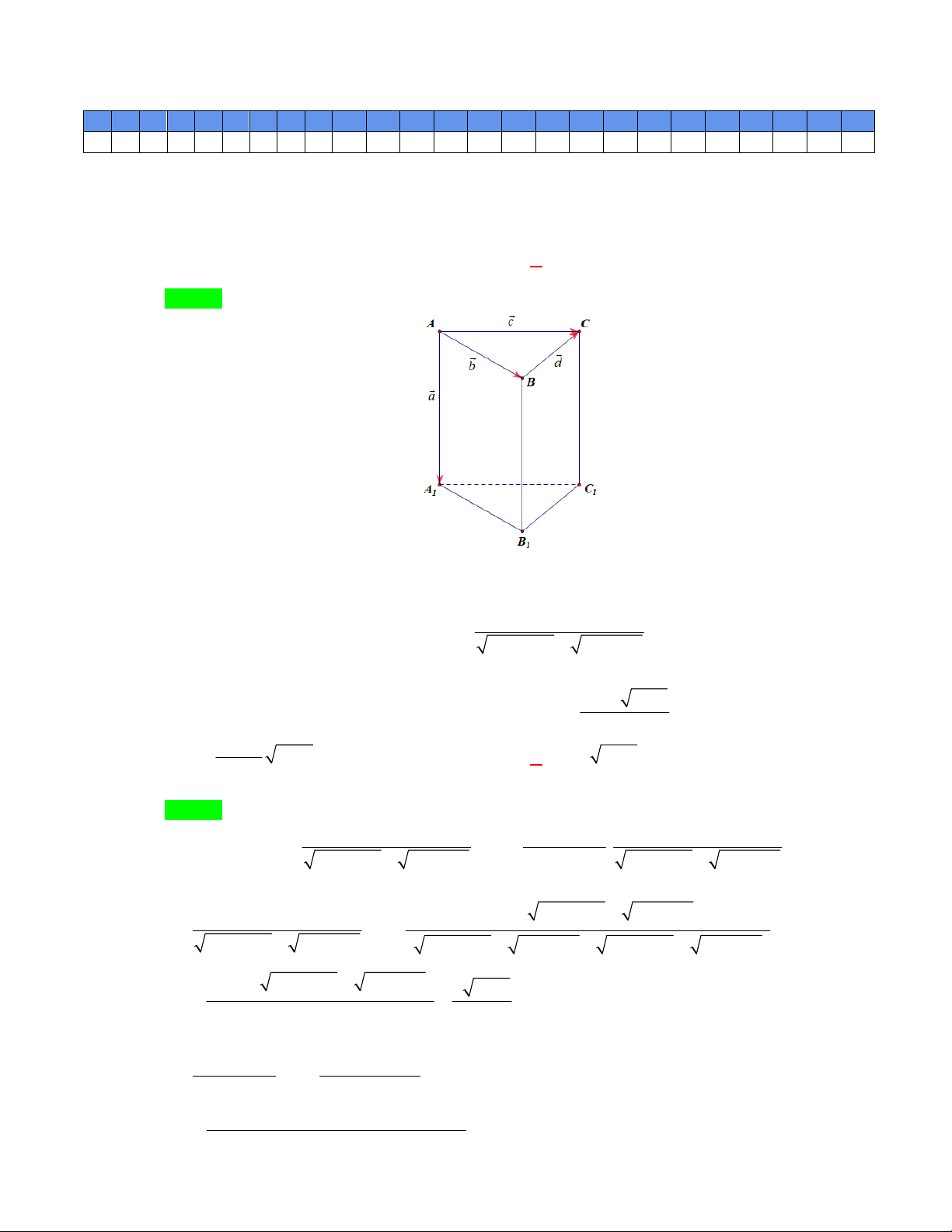
Câu 1. Cho hình lăng trụ tam giác ABC.A B C . Đặt AA  a, AB  b, AC  c, BC  d trong các đẳng thức 1 1 1 1
sau, đăng thức nào đúng?                
A. a  b  c  d .
B. a  b  c .
C. b  c  d  0 .
D. a  b  c  d  0 . 2016  x  x  2  khi x  1
Câu 2. Xác định giá trị thực k để hàm số f  x   2018x 1  x  2018
liên tục tại x  1 . 
k khi x  1 2017. 2018
A. k  1. B. k  . 2 20016 C. k  2019 .
D. k  2 2019 . 2017 1 n  
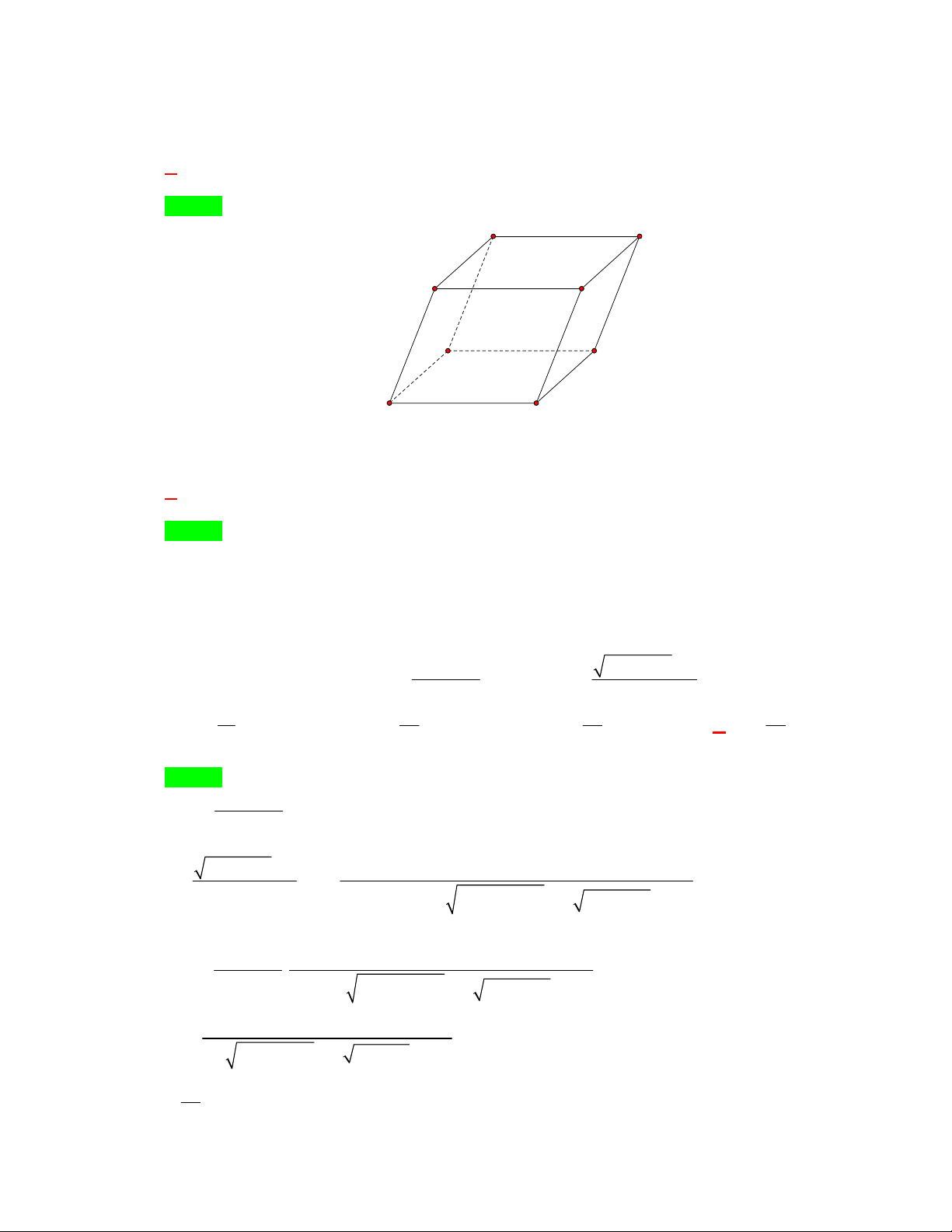
Câu 3. Kết quả của giới hạn lim   bằng  2  1 A. 0 . B.  . C. . D.  . 2
Câu 4. Trong các mệnh đề sau. Mệnh đề sai là
A. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau.
B. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
C. Hai mặt phẳng song song thì không có điểm chung.
D. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau. 2
x  ax 1 khi x  2
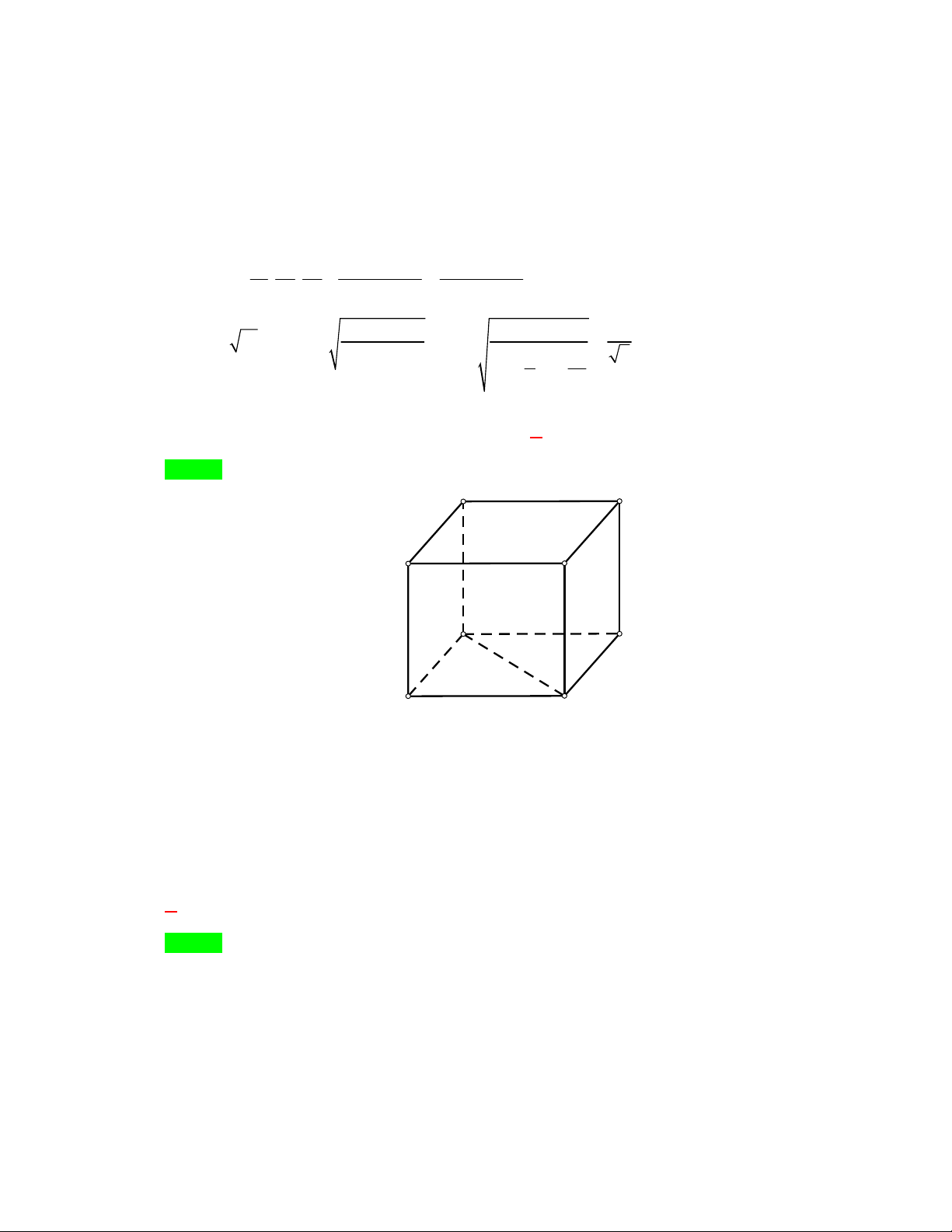
Câu 5. Tìm a để hàm số f  x  
có giới hạn khi x  2 2
2x  x 3a khi x  2 1 1 A. 1  . B. . C. 1. D. . 2 2 f  
1 . f 3. f 5... f 2n   1
Câu 6. Đặt f n  n  n  2 2
1 1, xét dãy số u sao cho u  . Tìm n  n
f 2. f 4. f 6... f 2n limn u . n  A. n u  . B. n u  n  1 lim . n  1 lim 3 2
C. limn u   2. D. limn u  n  3. n
Câu 7. Cho hình lập phương ABC .
D A' B 'C ' D ' . Tính góc giữa hai đường thẳng B ' D ' và A' . A A. 0 30 . B. 0 60 . C. 0 90 . D. 0 45 . 2
x  3x  2 khi x  1 
Câu 8. Để hàm số y  
liên tục tại điểm x  1 thì giá trị của a là 4x  a khi x  1  A. 4. B. 1. C. 1  . D. 4  .
Câu 9. Tìm tất cả các giá trị của tham số m để phương trình m   3 2
1 x  2mx  x  3m  0 có nghiệm thuộc khoảng 0;  1 1 1
A. m  0 .
B. 0  m  .
C. m  0 .
D. 0  m  . 3 3 Trang 1/13 - WordToan 2n
Câu 10. Kết quả của giới hạn lim bằng: 2 n 1 1 A. 3. B. 2 . C. 0 . D. . 3  1 1 1 
Câu 11. Kết quả của giới hạn lim  ...   bằng: 1.3 3.5
2n 12n 1      1 A. 0 . B. . C. 1. D.  . 2
Câu 12. Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
A. Hình bình hành.
B. Hình chữ nhật. C. Hình thoi. D. Hình thang. x  2
Câu 13. Cho hàm số y 
. Khẳng định nào dưới đây là đúng ? x 1
A. Hàm số gián đoạn tại x  1.
B. Hàm số liên tục trên  .
C. Hàm số liên tục trên  \   1  .
D. Hàm số liên tục tại x  1  .
Câu 14. Kết quả của giới hạn  2
lim n  n   1 bằng A.  . B. 2 n . C.  . D. 0 . 2 1 n  3n
Câu 15. Kết quả của giới hạn lim bằng 2n 1 1 1 A. 1. B. 2 . C. . D. . 4 2  
Câu 16. Cho tứ diện đều ABCD cạnh a . Tích vô hướng A . B CD bằng? 2 a 2 a A.  . B. . C. 2 a . D. 0 . 2 2
Câu 17. Cho hình hộp chữ nhật ABC . D AB C  D
  . Biểu thức nào sau đây đúng:
  
    A. A D   A B    A C  .
B. AB  AB  AA  AD .
   
   
C. AC  AB  AA  AD .
D. AD  AB  AD  AC .
Câu 18. Với giá trị nào của tham số m thì lim  2
mx  3x  2m  0. x 1  A. m  3  . B. m  1  .
C. m  0 .
D. m  3 . f (x)  20 3 6 f (x)  5  5
Câu 19. Cho f (x) là đa thức thỏa mãn lim  10 . Tình lim . x2 x  2 2 x2 x  x  6 4 12 6 4 A. T  . B. T  . C. T  . D. T  . 15 25 25 25
Câu 20. Phương trình 7 2
x  2x  x  5  0 có nghiệm thuộc khoảng nào dưới đây?. A. 0;  1 . B. 1;2 .
C. 1;0 . D. 2;3 .
Câu 21. Cho hình lăng trụ ABC.AB C
 . Gọi M , N lần lượt là trung điểm của BB và CC . Gọi  là giao
tuyến của hai mặt phẳng  AMN  và  AB C
  . Khẳng định nào sau đây đúng?.
A.  // BC .
B.  // AB .
C.  // AC .
D.  // AA . 2 x -5x + 6
Câu 22. Kết quả của giới hạn lim . x2 x -2 A. 1. B. -2 . C. 0 . D. -1. n x 1 -
Câu 23. Kết quả của giới hạn lim , ( *
m , n Î  ). 1 m x x 1 - n -1 n n +1 n! A. . B. . C. . D. . m -1 m m +1 m!
Câu 24. Cho hình hộp ABC . D AB C  D
  . Gọi M là trung điểm của AB . Mặt phẳng MAC cắt hình hộp ABC . D AB C  D
  theo thiết diện là hình gì?
Trang 2/13 – Diễn đàn giáo viên Toán
A. Hình thang.
B. Hình tam giác.
C. Hình ngũ giác.
D. Hình lục giác.
Câu 25. Kết quả của giới hạn lim  2 x  3x   1 bằng: x 1  A. 2 . B. 0 . C. 1. D. 1.
PHẦN II: TỰ LUẬN (5 ĐIỂM)
Câu 26. (3 điểm) Tính các giới hạn sau: 2n  2017 2 x  3x 10 3
x 1  x  5 a) lim . b) lim . c) lim . 3n  2018 x2 x  2 x3 x  3
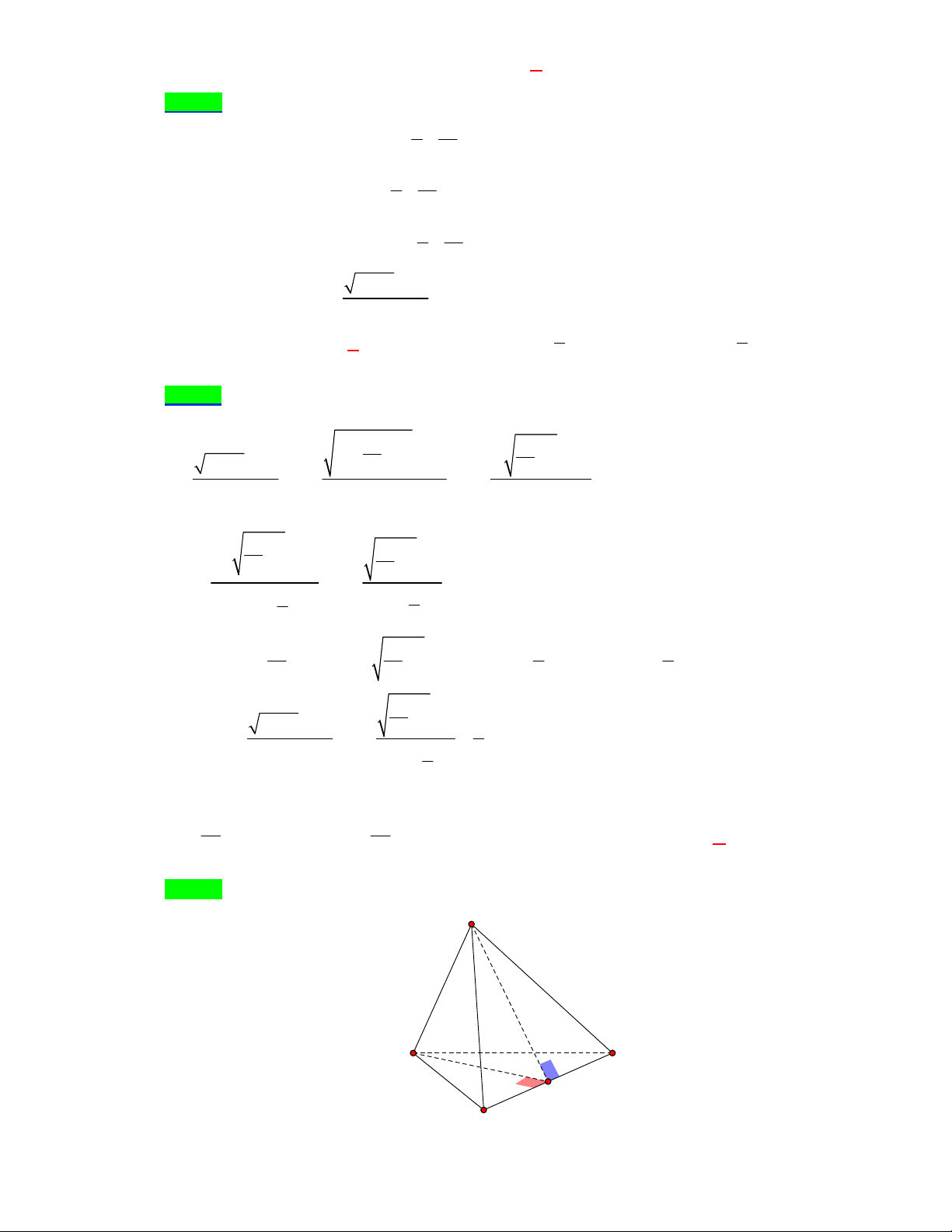
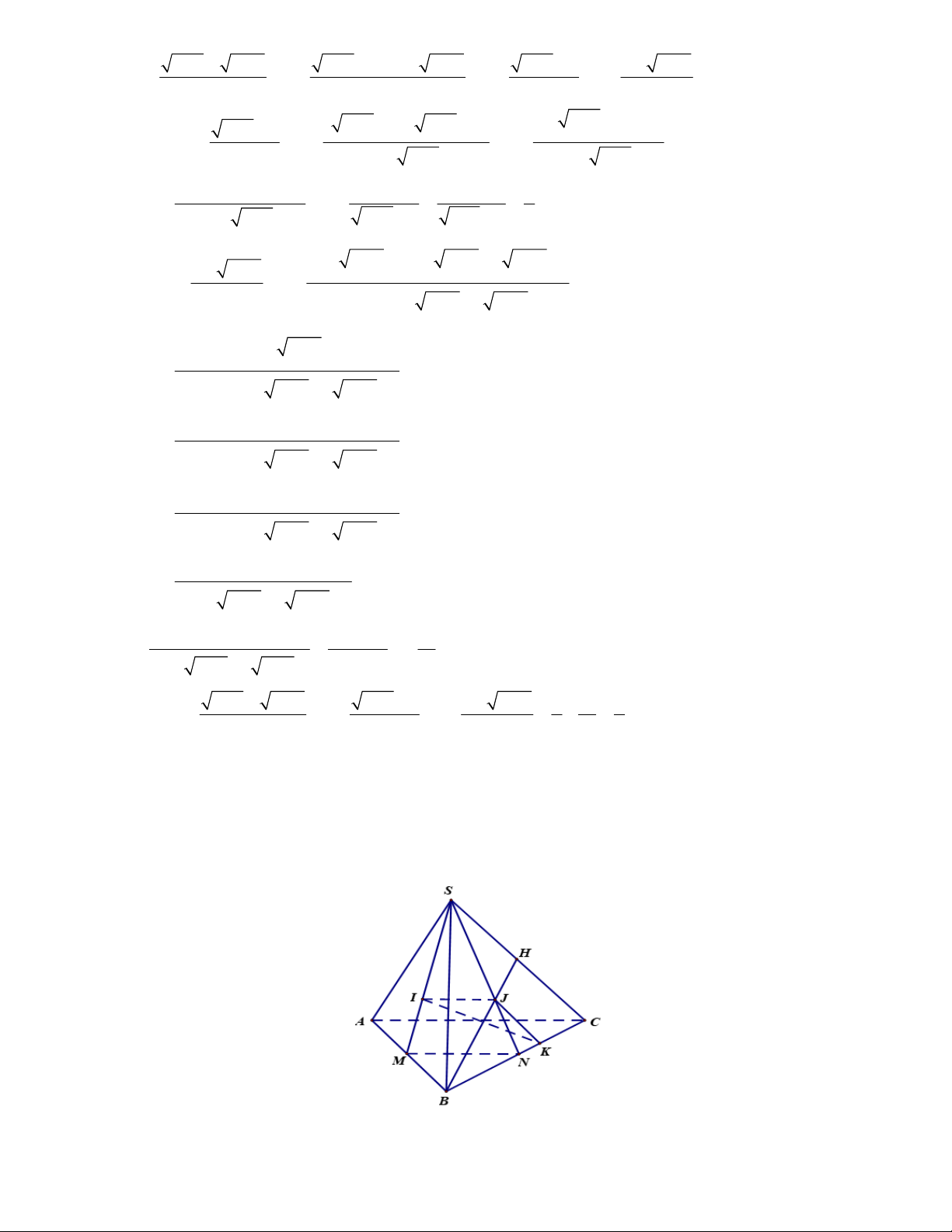
Câu 27. (1,5 điểm) Cho tứ diện đều SABC cạnh a . Gọi I , J lần lượt là trọng tâm tam giác SBA, SBC , K là
điểm trên cạnh BC sao cho BC  3CK .
a) Chứng minh IJK  / / SAC .
b) Xác định và tính diện tích thiết diện của hình chóp cắt bởi IJK  .
Câu 28. (0,5 điểm) Tìm tất cả các giá trị của tham số m để phương trình 3 2
x  3x  2m  2 x  m  3  0 có
ba nghiệm x , x , x thỏa mãn x  1
  x  x . 1 2 3 1 2 3
------------- HẾT ------------- Trang 3/13 - WordToan
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5 ĐIỂM) BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D A D A B C A B C B D C C B D C A D B A D B A D
LỜI GIẢI CHI TIẾT        
Câu 1. Cho hình lăng trụ tam giác ABC.A B C . Đặt AA  a, AB  b, AC  c, BC  d trong các đẳng 1 1 1 1
thức sau, đăng thức nào đúng?                
A. a  b  c  d .
B. a  b  c .
C. b  c  d  0 .
D. a  b  c  d  0 . Lời giải Chọn C
Đẳng thức C đúng vì   
         
b  c  d  0  AB  AC  BC  0  CB  BC  0  CC  0 . 2016  x  x  2  khi x  1
Câu 2. Xác định giá trị thực k để hàm số f  x   2018x 1  x  2018
liên tục tại x  1 .  k khi x 1 2017. 2018
A. k  1. B. k  . 2 20016 C. k  2019 .
D. k  2 2019 . 2017 Lời giải Chọn D 2016 2016 x  x  2  x  x  2 x 1 
Xét lim f  x  lim  lim .  . x 1  x 1  x 1
2018x 1  x  2018  x  1
2018x 1  x  2018  Ta có x 
x  1 2018x1 x2018 1  lim  lim x 1  x 1
2018x 1  x  2018
  2018x 1  x  2018 2018x 1  x  2018
x  1 2018x 1 x 2018 2 2019  lim  . x 1  2017  x   1 2017 Lại có 2016 2016 x  x  2 x 1 x 1 lim  lim x 1  x 1 x 1  x 1
x  1 2015 2014 x  x  ... x   1  x 1  lim  2017 . x 1  x 1
Trang 4/13 – Diễn đàn giáo viên Toán
Vậy lim f  x  2 2019 . x 1 
Hàm số f  x liên tục tại x  1 khi và chỉ khi lim f  x  f  
1  2 2019  k . x 1  1 n  
Câu 3. Kết quả của giới hạn lim   bằng  2  1 A. 0 . B.  . C. . D.  . 2 Lời giải Chọn A Có lim n
q  0 nếu q  1 . 1 1 n   Vì  1 nên lim  0   . 2  2 
Câu 4. Trong các mệnh đề sau. Mệnh đề sai là
A. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau.
B. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
C. Hai mặt phẳng song song thì không có điểm chung.
D. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau. Lời giải Chọn D
Phương án A, B, C đúng theo các tính chất của hai mặt phẳng song
Phương án D sai vì hai mặt phẳng không phân biệt nên chúng có thể trùng nhau 2
x  ax 1 khi x  2
Câu 5. Tìm a để hàm số f  x  
có giới hạn khi x  2 2
2x  x 3a khi x  2 1 1 A. 1  . B. . C. 1. D. . 2 2 Lời giải Chọn A
Ta có lim f  x  lim        2 x ax 1 5 2a x 2  x 2 
lim f  x  lim        2 2x
x 3a 6 3a x 2  x 2 
Hàm số có giới hạn khi x  2 khi và chỉ khi lim f  x  lim f  x  5  2a  6  3a  a  1  x 2 x 2   Vậy a  1  f  
1 . f 3. f 5... f 2n   1
Câu 6. Đặt f n  n  n  2 2
1 1, xét dãy số u sao cho u  . Tìm n  n
f 2. f 4. f 6... f 2n limn u . n  A. n u  . B. n u  n  1 lim . n  1 lim 3 2
C. limn u   2. D. limn u  n  3. n Lời giải Chọn B Ta có: Trang 5/13 - WordToan
f n  n   2 2
1  n 1  n  4
1  2nn  2 1   2 n   1    n  4
1  2nn 1 2n  n   1    n  4 2 2 2 1  4n    2 n   1 2n   1    n  
1 n  4n   1  n   1 2n   1  n   1   n  2 2 2 2 2 1 1  
Từ đó ta có: f  k     k  2    2 2 1 2 1 1 . 4k   1  
f  k    k  2    2 2 2 1 1 . 4k   1   2 10 26 2n  2 1 1 2 Suy ra u  . . ...  n 10 26 50 2n  2 1 1 2n  2 1 1     n u   n    . n  2 2 1 lim lim . lim  2n  2 2 1 1   1  1 2   2     2  n  n
Câu 7. Cho hình lập phương ABC .
D A' B 'C ' D ' . Tính góc giữa hai đường thẳng B ' D ' và A' . A A. 0 30 . B. 0 60 . C. 0 90 . D. 0 45 . Lời giải Chọn C B C A D B' C' A' D' 
  
  Vì ABC .
D A' B 'C ' D ' là hình lập phương nên ta có A ' A  B ' B; B ' A '.B ' B  B 'C '.B ' B  0 và
  
B' D'  B' A'  B'C ' .
 
      
Khi đó B ' D'.A' A  B' A' B'C'.B'B  B' A'.B'B  B'C'.B'B  0  B'D'  A' A. Vậy B D A A 0 ' ', '  90 . 2
x  3x  2 khi x  1 
Câu 8. Để hàm số y  
liên tục tại điểm x  1
 thì giá trị của a là 4x  a khi x  1  A. 4. B. 1. C. 1  . D. 4  . Lời giải Chọn A
Hàm số liên tục tại điểm x  1
  lim f x  lim f x  f   1 (*). x   1  x   1        f   1   2 1  3  1  2  0 
Với  lim f  x  lim    .    2 x 3x 2 0 x  1 x  1 
 lim f x  lim 4x  a  a  4 x   1 x  1 
*  a  4  0  a  4.
Trang 6/13 – Diễn đàn giáo viên Toán
Câu 9. Tìm tất cả các giá trị của tham số m để phương trình m   3 2
1 x  2mx  x  3m  0 có nghiệm thuộc khoảng 0;  1 1 1
A. m  0 .
B. 0  m  .
C. m  0 .
D. 0  m  . 3 3 Lời giải Chọn B
Đặt f  x  m   3 2
1 x  2mx  x  3m .  f  0  3m Ta có  .  f    1  6m  2
Phương trình có nghiệm thuộc khoảng 
  f   f     m m   1 0;1 0 . 1 0 3 6
2  0  0  m  3 2n
Câu 10. Kết quả của giới hạn lim bằng: 2 n 1 1 A. 3. B. 2 . C. 0 . D. . 3 Lời giải Chọn C 2 2n 0 Ta có : lim
 lim n   0 2 n 1 1 1 1 2 n  1 1 1 
Câu 11. Kết quả của giới hạn lim  ...   bằng: 1.3 3.5
2n 12n 1      1 A. 0 . B. . C. 1. D.  . 2 Lời giải Chọn B 1 1  1 1  Với mọi * k   thì     , do đó 2k   1 2k   1
2  2k 1 2k 1  1 1 1  1  1 1 1 1 1 1  1  1 lim    ...    lim 1      lim 1  1.3 3.5
2n 12n 1          2 
3 3 5 2n 1 2n 1 2  2n 1 2 .
Câu 12. Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
A. Hình bình hành.
B. Hình chữ nhật. C. Hình thoi. D. Hình thang. Lời giải Chọn D
Hình chữ nhật có hai cặp cạnh đối song song nên hình chiếu của nó không thể là hình thang. x  2
Câu 13. Cho hàm số y 
. Khẳng định nào dưới đây là đúng ? x 1
A. Hàm số gián đoạn tại x 1.
B. Hàm số liên tục trên  .
C. Hàm số liên tục trên  \   1 .
D. Hàm số liên tục tại x  1  . Lời giải Chọn C
Ta có Tập xác định của hàm số D   ;   
1  1; do đó hàm số liên tục trên các khoảng ; 
1 và 1; .
Câu 14. Kết quả của giới hạn  2
lim n  n   1 bằng Trang 7/13 - WordToan A.  . B. 2 n . C.  . D. 0 . Lời giải Chọn C   1 1  Ta có lim 2 n  n   2 1  lim n 1    . 2   n n     1 1  Mặt khác: 2
limn   ; lim 1   1  . 2   n n    1 1  Suy ra lim 2 n  n   2 1  lim n 1      . 2   n n    2 1 n  3n
Câu 15. Kết quả của giới hạn lim bằng 2n 1 1 1 A. 1. B. 2 . C. . D. . 4 2 Lời giải Chọn B Ta có: 2  1  1 n 1  3n     2 2 n. 1 3n 2 1 n  3n  n  lim  lim  lim n 2n 1 2n 1 2n 1  1  1 n 1  3 2 1  3 n 2 lim     lim n .  1  1 n 2  2     n  n 1  1   1   1  Mặt khác: lim  0  lim 1  3  4 ; lim  0  lim 2   2 . 2 2 n  n         n   n  1   2 1 3 2 1 n  3n n 4 Suy ra: lim  lim   2 . 2n 1 1 2 2  n  
Câu 16. Cho tứ diện đều ABCD cạnh a . Tích vô hướng A . B CD bằng? 2 a 2 a A.  . B. . C. 2 a . D. 0 . 2 2 Lời giải Chọn D A B D M C
Gọi M là trung điểm của . CD
Trang 8/13 – Diễn đàn giáo viên Toán CD   BM  
Vì ABCD là tứ diện đều nên 
 CD   ABM   CD  AB  C . D AB  0. CD   AM
Câu 17. Cho hình hộp chữ nhật ABC . D AB C  D
  . Biểu thức nào sau đây đúng:
  
    A. A D   A B    A C  .
B. AB  AB  AA  AD .
   
   
C. AC  AB  AA  AD .
D. AD  AB  AD  AC . Lời giải Chọn C A' B' D' C' A B D C
   
Theo qui tắc hình hộp thấy AC  AB  AA  AD đúng.
Câu 18. Với giá trị nào của tham số m thì lim  2
mx  3x  2m  0. x 1  A. m  3  . B. m  1  .
C. m  0 .
D. m  3 . Lời giải Chọn A Ta có: lim  2
mx  3x  2m  0 x1  . m  2 1  3.  1  2m  0  m  3 f (x)  20 3 6 f (x)  5  5
Câu 19. Cho f (x) là đa thức thỏa mãn lim  10 . Tình lim . x2 x  2 2 x2 x  x  6 4 12 6 4 A. T  . B. T  . C. T  . D. T  . 15 25 25 25 Lời giải Chọn D f (x)  20 Vì lim
 10 nên f (x)  20 khi x  2 x2 x  2 Ta có: 3 6 f (x)  5  5 6 f (x)  5 125 lim  lim 2 x2 x2 x  x  6
x  2x 3 6 f (x) 52 3  3
 5. 6 f (x)  5  25      f (x)  20 6   lim  .  x2 x  2 
x 3 6 f (x) 52 3  3
 5. 6 f (x)  5  25       6  10.5. 6. 5 2 3 3 20 5. 6.20 5 25       4  . 25
Câu 20. Phương trình 7 2
x  2x  x  5  0 có nghiệm thuộc khoảng nào dưới đây?. Trang 9/13 - WordToan A. 0;  1 . B. 1;2 .
C. 1;0 . D. 2;3 . Lời giải Chọn B
Xét hàm số f  x 7 2
 x  2x  x  5 liên tục trên D  . Ta có: f   1  3
  0 ; f 2 129  0. Ta thấy f  
1 . f 2  0 do đó f  x  0 có nghiệm thuộc khoảng 1;2 .
Câu 21. Cho hình lăng trụ ABC.AB C
 . Gọi M , N lần lượt là trung điểm của BB và CC . Gọi  là giao
tuyến của hai mặt phẳng  AMN  và  AB C
  . Khẳng định nào sau đây đúng?.
A.  // BC .
B.  // AB .
C.  // AC .
D.  // AA . Lời giải Chọn A A B C M N A' B' C' I
Theo bài ra ta có: BC // MN // B C   . Trong  ACC A
  gọi I  AN  AC.
Khi đó hai mặt phẳng  AMN  và  AB C
  có điểm chung I và lần lượt đi qua hai đường thẳng
song song MN ; B C  .
Do đó, giao tuyến của hai mặt phẳng  AMN  và  AB C
  là đường thẳng  qua I và song song với B C
    // BC . 2 x -5x + 6
Câu 22. Kết quả của giới hạn lim . x2 x -2 A. 1. B. -2 . C. 0 . D. -1. Lời giải
Chọn D (x-2)(x- )3 Có lim = lim(x- ) 3 = 2-3 = 1 - . x2 x2 x -2 n x 1 -
Câu 23. Kết quả của giới hạn lim , ( *
m , n Î  ). 1 m x x 1 - n -1 n n +1 n! A. . B. . C. . D. . m -1 m m +1 m! Lời giải Chọn B Ta có
Trang 10/13 – Diễn đàn giáo viên Toán n x 1 - n n 1 - n 1 - n-2 n-2 x - x + x - x + x +...- x + x -1 lim = lim 1 m x x 1 - m m 1 - m 1 - m 2 - m-2 x 1  x - x + x - x + x +...- x + x -1 n 1 x - (x- ) n 2 1 + x - (x- ) 1 +...+(x- ) 1 (x- ) 1 ( n 1 - n-2 x + x +...+ ) 1 = lim = lim m 1 x x - (x- ) m 2 1 1 + x -  (x- ) 1 +...+(x- ) 1 x (x - ) 1 ( m 1 - m-2 1 x + x +...+ ) 1 n 1 - n-2 x + x +...+1 n = lim = . m 1 - m-2 x 1  x + x +...+1 m
Câu 24. Cho hình hộp ABC . D AB C  D
  . Gọi M là trung điểm của AB . Mặt phẳng MAC cắt hình hộp ABC . D AB C  D
  theo thiết diện là hình gì? A. Hình thang.
B. Hình tam giác.
C. Hình ngũ giác.
D. Hình lục giác. Lời giải Chọn A B C A D B' C' A' D'
Gọi N là trung điểm của BC , ta có MN //AC//AC nên MN  MAC .
MAC ABB A
   MA ;MAC  ABCD  MN 
MAC BCC B
   NC ;MAC AB C  D
   AC
Thiết diện thu được là tứ giác MNC A
 . Do MN //AC nên MNC A
  là hình thang.
Câu 25. Kết quả của giới hạn lim  2 x  3x   1 bằng: x 1  A. 2 . B. 0 . C. 1. D. 1. Lời giải Chọn D
Dễ thấy f  x 2
 x  3x 1 liên tục tại x  1 nên lim  2 x  3x   1  f   1  1 . x 1 
PHẦN II: TỰ LUẬN (5 ĐIỂM)
Câu 26. (3 điểm) Tính các giới hạn sau: 2n  2017 2 x  3x 10 3
x 1  x  5 a) lim . b) lim . c) lim . 3n  2018 x2 x  2 x3 x  3 Lời giải  2017   2017  n 2  2  2n 2017      a)  n   n lim lim lim    3n  2018  2018   2018  n 3  3       n   n   2017  2017 lim 2    lim 2  lim  n  2  0 2 n      2018  2018 3  0 3 lim 3  lim 3  lim    n  n 2 x  3x 10
x  2x 5 b) lim  lim
 limx  5  2  5  7 x2 x2 x2 x  2 x  2 Trang 11/13 - WordToan 3 3 3
x 1  x  5
x 1  2  2  x  5 x 1  2 2  x  5 c) lim  lim  lim  lim x3 x3 x3 x3 x  3 x  3 x  3 x  3
 x   x   x       x 12 22 1 2 1 2 1 2  Ta có: lim  lim  lim x3 x3 x  3
x 3 x 1 2
x3  x  3 x 1  2 x 3 1 1 1  lim  lim  
x3  x  3 x 1  2 x3 x 1  2 3 1  2 4        x 
2 x 54 2 x 5  x 5 2 5 2 3 3 3 3  Có: lim  lim x x  3 x
x 342 x5  x52 3 3 3 3  2  x53 3 3   lim
x x 342 x5  x52 3 3 3  8 x 5  lim
x x 342 x5  x52 3 3 3  3 x  lim
x x 342 x5  x52 3 3 3  1   lim
x 42 x5  x52 3 3 3  1 1  1           2 3 3 4  4  4 12 4 2 3 5 3 5 3 3
x 1  x  5 x 1  2 2  x  5 1 1 1 Vậy: lim  lim  lim    x3 x3 x3 x  3 x  3 x  3 4 12 6
Câu 27. (1,5 điểm) Cho tứ diện đều SABC cạnh a . Gọi I , J lần lượt là trọng tâm tam giác SBA, SBC , K là
điểm trên cạnh BC sao cho BC  3CK .
a) Chứng minh IJK  / / SAC .
b) Xác định và tính diện tích thiết diện của hình chóp cắt bởi IJK  . Lời giải
a) Gọi M , N , H lần lượt là trung điểm của AB , BC , SC . IJ / /MN Ta có 
 IJ / / AC  IJ / / SAC(1) . MN / / AC
Trang 12/13 – Diễn đàn giáo viên Toán JH CK 1 Có 
  JK / /HC  JK / / SAC(2) . BH BC 3
Từ (1) và (2)  IJK  / / SAC . b) S E I J A C F K M N B
+)Trong SBC gọi E  JK  SB  E IJK  .
Trong SAB gọi F  IE  AB  F IJK  .
Suy ra IJK  SAB  EF .
IJK  ABC  FK .
IJK SBC  KE .
Vậy thiết diện là tam giác EFK . EK EF FK 2 +)Ta có    SC SA AC 3 2a
Mà SC  SA  AC  a  EF  FK  KE  . 3
Suy ra tam giác EFK đều. 2 2  2a  3 a 3 Vậy S  .  . EF  K    3  4 9
Câu 28. (0,5 điểm) Tìm tất cả các giá trị của tham số m để phương trình 3 2
x  3x  2m  2 x  m  3  0 có
ba nghiệm x , x , x thỏa mãn x  1
  x  x . 1 2 3 1 2 3 Lời giải Điều kiện cần:
Đặt f  x 3 2
 x  3x  2m  2 x  m  3 thì f x liên tục trên . 
Từ giả thiết phương trình có nghiệm x  1
  x  x . Do lim f x   nên ta suy ra 1 2 3 x f  
1  0  m  5  0  m  5
 . Ta chứng minh đó cũng là điều kiện đủ. Điều kiện đủ: Giả sử m  5.
 Thế thì từ f  
1  m  5  f   1  0.
Vì lim f  x   và do hàm f  x liên tục trên  nên suy ra phương trình có nghiệm x  1.  1 x
Lại có f 0  m  3  0 (do m  5
 ). Nên phương trình có nghiệm 1   x  0. 2
Lại do tính liên tục của f  x trên  và lim f  x   nên phương trình có nghiệm 0  x . 3 x
Vậy điều kiện cần và đủ để phương trình có nghiệm x , x , x thỏa x  1
  x  x là m  5.  1 2 3 1 2 3
------------- HẾT ------------- Trang 13/13 - WordToan