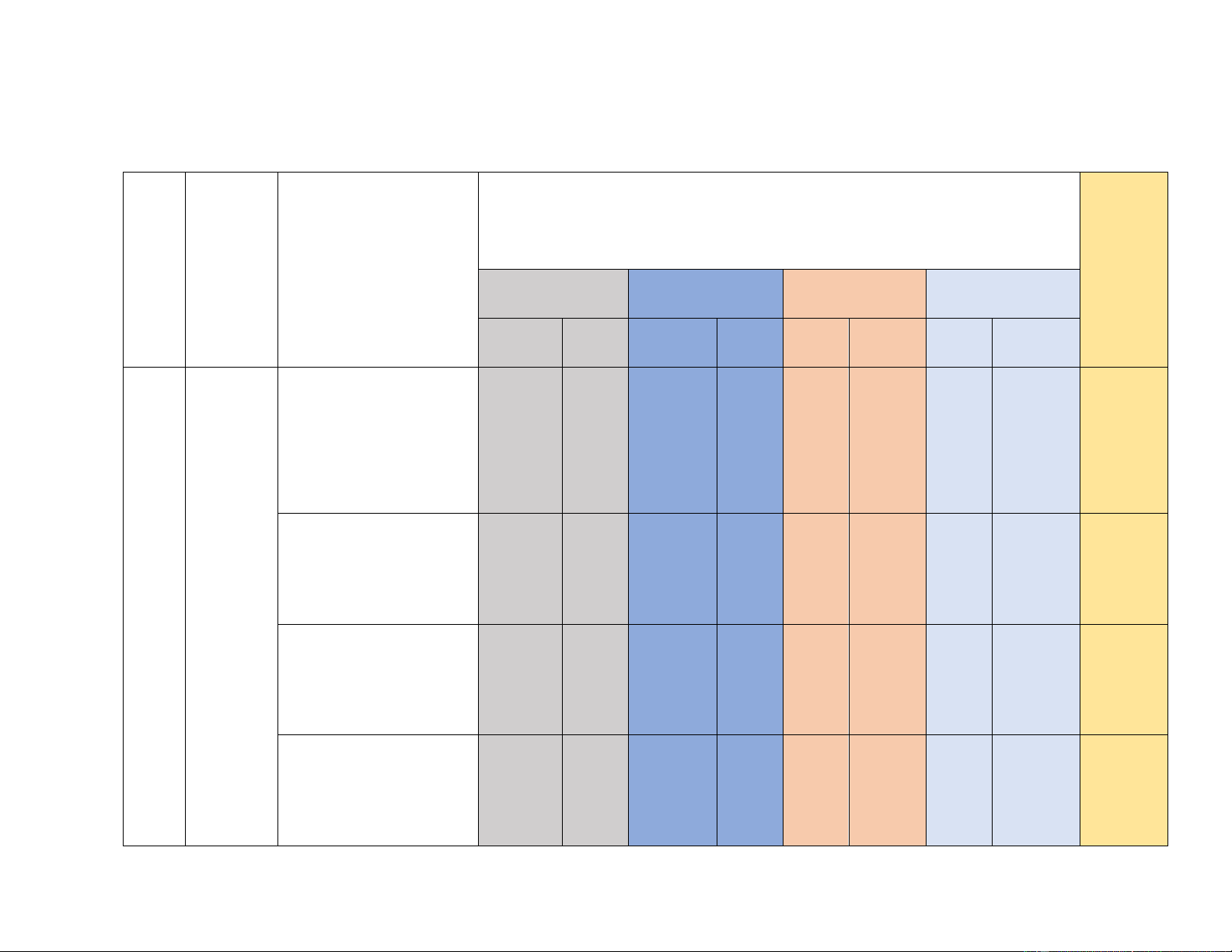
BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 8 NĂM HỌC 2023 - 2024
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Nội dung/
Số câu/ý hỏi theo mức độ nhận thức Chương/ TT Đơn vị kiến
Mức độ đánh giá Thông Vận Chủ đề Nhận biết Vận dụng thức hiểu dụng cao Đa thức Nhận biết: nhiều biến.
– Nhận biết được các khái niệm về 2 c TN Các phép Biểu
đơn thức, đa thức nhiều biến. 1 đ toán cộng, 1
thức đại trừ, nhân, Thông hiểu: số chia các đa
– Tính được giá trị của đa thức khi 1/3 c TL thức nhiều
biết giá trị của các biến. 0,75 đ biến. Vận dụng:
– Thực hiện được các phép tính: phép 1/3 c TL
cộng, phép trừ, phép nhân các đa thức 0,75 đ
nhiều biến trong những trường hợp đơn giả n. – 1/3 c
Thực hiện được phép chia hết một
đa thức cho một đơn thức trong những 0,5 đ trường hợp đơn giản. Nhận biết: 2c TN 1/2 c TL 1/2 c TL
– Nhận biết được các khái niệm: đồng 1 đ 0,5 đ 0,5 đ
nhất thức, hằng đẳng thức. Hằng đẳng thức Thông hiểu: đáng nhớ
– Mô tả được các hằng đẳng thức:
bình phương của tổng và hiệu; hiệu hai bình phương. Vận dụng: 1 c TL
- Chứng minh đa thức không phụ 1đ thuộc vào biến 2 Nhận biết
– Nhận biết được mối quan hệ giữa
các cạnh, góc, đường chéo của các
hình đã học (Hình thang cân, hình chữ nhật)
Tính chất và dấu hiệu Thông hiểu Tứ giác
nhận biết các - Tính góc của hình thang cân và so 2c TN
tứ giác đặc
sánh độ dài 2 đoạn thẳng thông qua 1đ biệt
tính chất đường chéo hình chữ nhật
- Hiểu cách chứng minh một hình là tứ giác đặc biệt. 2/3c TL 2 đ
- Hiểu tính chất đường chéo của hình bình hành. Vận dụng
– Sử dụng thành thạo, linh hoạt các 1/3 c TL
kiến thức đã học về tứ giác vào chứng 1 đ minh hình thang cân Tổng Câu 4 7/2 3/2 1 Điểm 2 đ 4 đ 3 đ 1 đ Tỉ lệ chung 20 % 40 % 30 % 10%
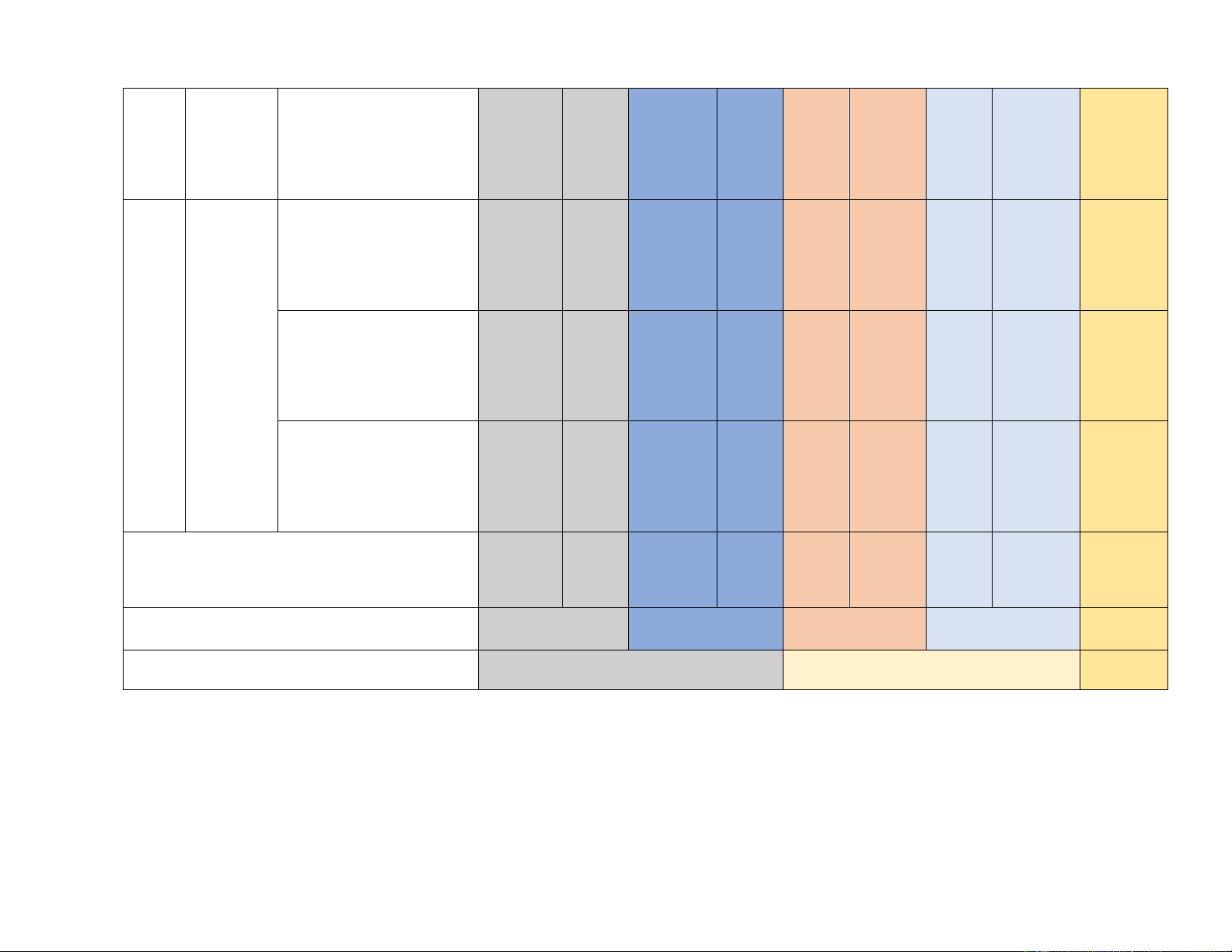
KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ I - MÔN TOÁN – LỚP 8
TRẮC NGHIỆM 3 ĐIỂM + TỰ LUẬN 7 ĐIỂM
Mức độ đánh giá Tổng Chương/ Nội dung/ % điểm TT (4-11) Chủ đề
đơn vị kiến thức (12) (1) Nhận biết Thông hiểu Vận dụng Vận dụng cao (2) (3) TN TL TN TL TN TL TN TL 2 1/3 Đa thức, cộng, trừ Câu 1,2 Câu 8 đa thức nhiều biến. 1,75 đ 1 đ 0,75 đ Biểu 17,5% thức 1/3 Chia đa thức cho đại số Câu 8 0,5 đ đơn thức 0,5 đ 5% 1/3 6 đ Giá trị của đa thức Câu 8 0,75 đ 60% 0,75 đ 7,5% 2 1/2 1/2 Hằng đẳng thức Câu 3,4 Câu 7 Câu 7 2 đ 1 đ 0,5 đ 0,5 đ 20% Chứng minh không 1 phụ thuộc vào biến Câu 10 1đ 1 đ 10% 1 1/3 Hình thang cân Câu 5 Câu 9 1,5 đ Các tứ 0,5 đ 1 đ 15% giác Hình bình hành 2/3 đặc biệt Câu 9 2 đ 2 đ 20% 4 đ Hình chữ nhật 1 40 % Câu 6 0,5 đ 0,5 đ 5 % Tổng 4 2 3/2 3/2 1 10 Điểm 2 đ 1 đ 3đ 3đ 1đ 10đ Tỉ lệ % 20% 40% 30% 10% 100 Tỉ lệ chung 60% 40 % 100
ĐỀ KIỂM TRA GIỮA HỌC KÌ I - NĂM HỌC 2023-2024 MÔN TOÁN LỚP 8
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM (3 điểm).
Chọn đáp án đúng nhất trong các phương án sau:
Câu 1: Biểu thức nào KHÔNG LÀ đa thức ? A. 9 x2y B. 2xy + xy2 2 C. -2x z D. 3x - 2 xy 2
Câu 2: Phần hệ số và phần biến của đơn thức - x y là :
A. Hệ số là -1, phần biến là x,y. 2
B. Hệ số là -1, phần biến là x y
C. Hệ số là 1, phần biến là x2y. 2
D. Hệ số là -1, phần biến là xy
Câu 3: Biểu thức (x - y)2 có kết quả của khai triển là : 2 2 2 2 2 2 2 2 A. x + 2xy - y B. x + 2xy + y C. x - 2xy + y D. x + xy + y
Câu 4: Cho biểu thức 2 2
x - y = (.........)(x + y) điền vào chỗ “...” để được hằng đẳng thức đúng: A. x - y B. x + y C. xy D. 2xy
Câu 5: Cho hình thang cân ABCD (AB // CD) có = 70o A . Số đo góc C là: A. 0 C = 70 B. 0 C = 110 C. 0 C = 80 D. 0 C = 140
Câu 6: Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Khẳng định nào sau đây SAI: A. AB = CD B. AD // BC C. OC = CD D. OA > OC
PHẦN II. TỰ LUẬN (7 điểm). Câu 7 (1 điểm):
1. Viết hằng đẳng thức diễn tả theo lời văn: Bình phương một tổng của 2 số x và y.
2. Viết đa thức sau dưới dạng tích: 2 x − 25 Câu 8 (2 điểm):
1. Thực hiện phép chia đa thức 3 2 2 A = 5x y - 3x y + xy cho xy 2. Cho đa thứ 3 2 3 2
c : M = x - x y + 2xy + 3 và P = 3x - 2x y - xy + 3. Tìm đa thứ c A biết: A + 2M = P 2
3. Tính giá trị của đa thức N biết : 2 N= 9x - 12x + 4 tại x = 3
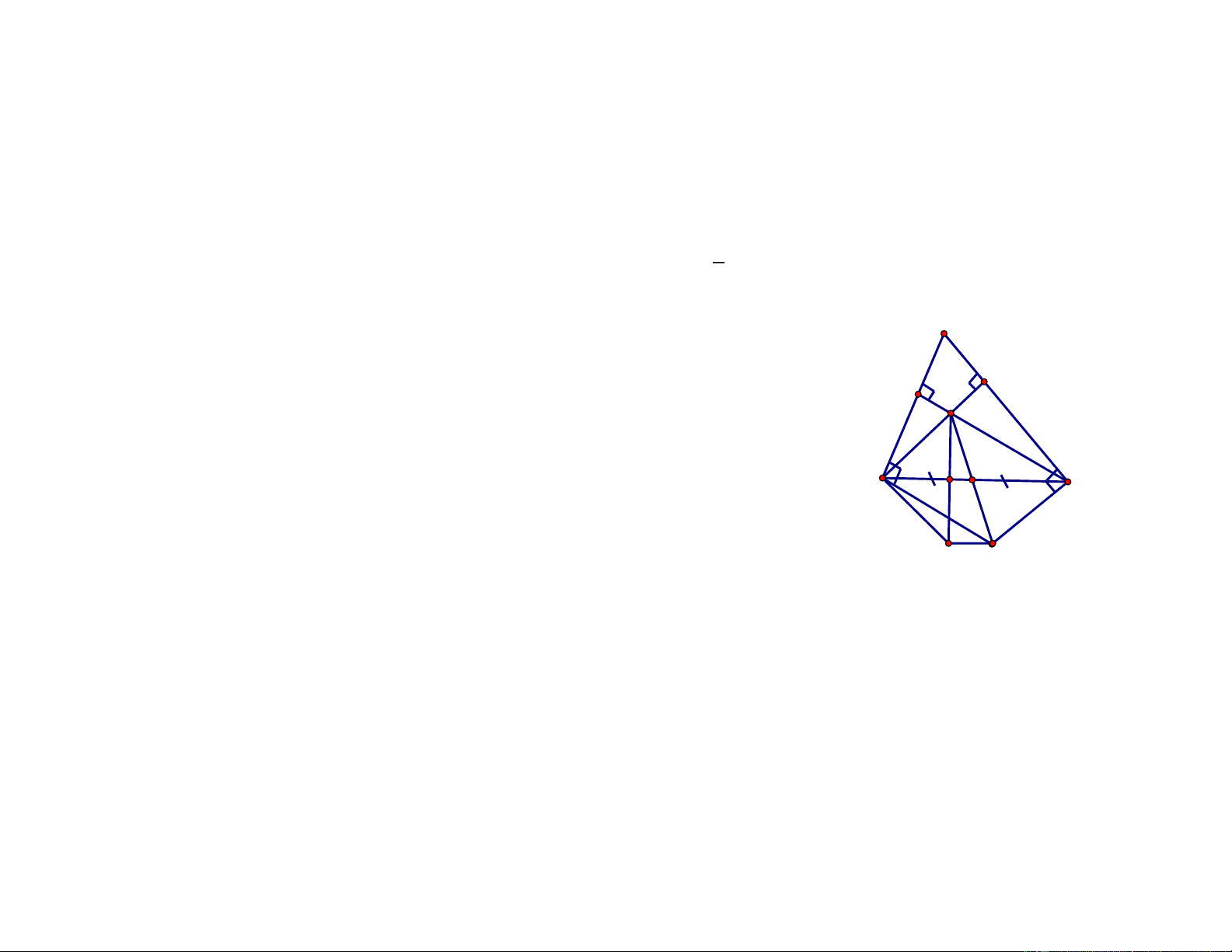
Câu 9 (3 điểm): (Học sinh vẽ lại hình vào bài làm). A
Cho tam giác ABC nhọn (AB < AC), đường cao BE và CF cắt nhau tại H.
Qua C, D kẻ các đường thẳng vuông góc với AC, AD cắt nhau tại K. E
a) Tứ giác BHCK là hình gì? F H
b) Gọi M là trung điểm của BC. Chứng minh H, M, K thẳng hàng.
c) Từ H kẻ HG vuông góc với BC (G thuộc BC). B G
Lấy I thuộc tia đối của tia GH. Chứng minh: BCKI là hình thang cân. M C
Câu 10 (1 điểm): Chứng minh đa thức sau không phụ thuộc vào x: ( I K 2 )( 2 )( 4 )( 8 )( 16 )( 32 ) 64
C= x - 1 x + 1 x + 1 x + 1 x + 1 x + 1 - x
----------- HẾT ----------- HƯỚNG DẪN CHẤM
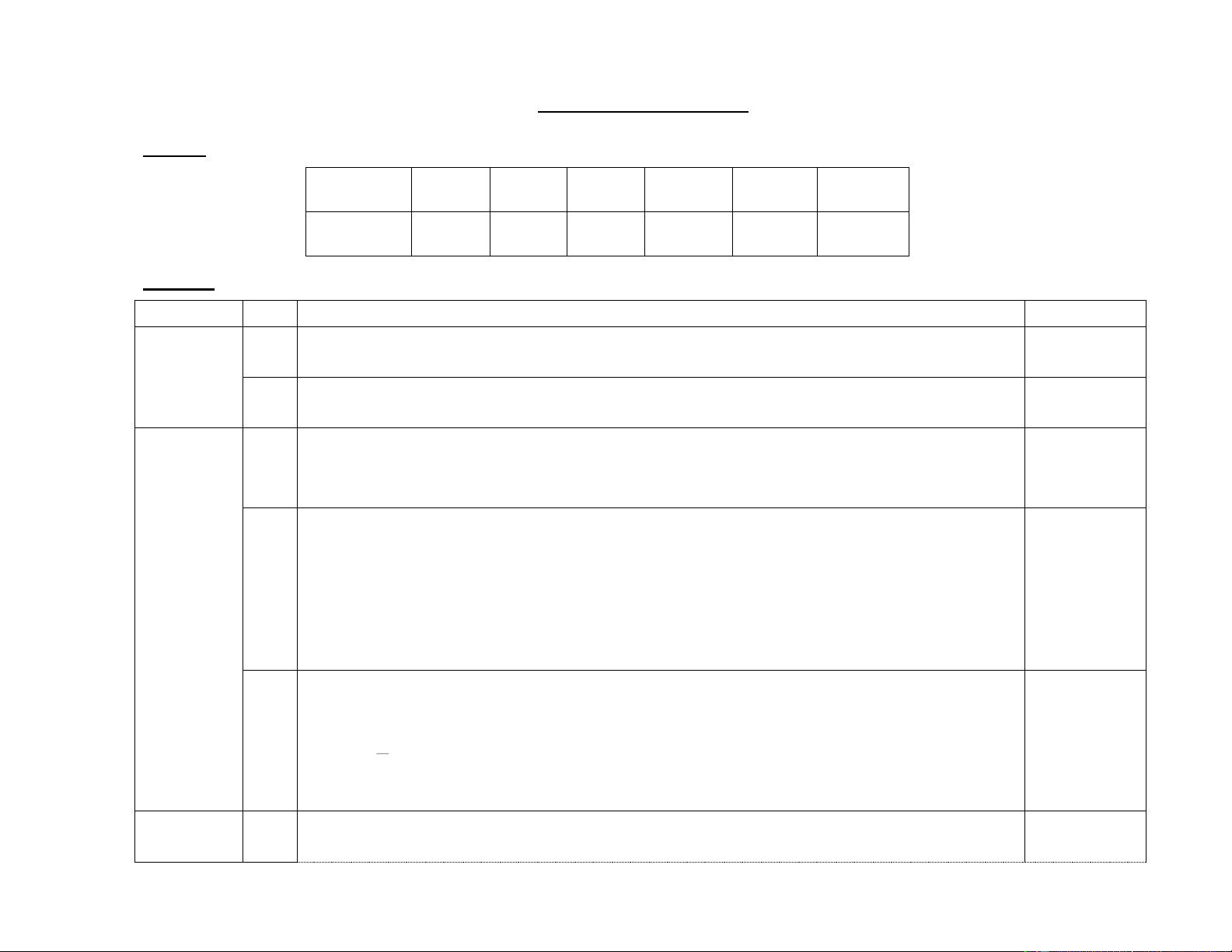
Phần I. TRẮC NGHIỆM (3 điểm): Mỗi ý đúng được 0,5 điểm. Câu 1 2 3 4 5 6 Đáp án D B C A B D
Phần II. TỰ LUẬN (7 điểm). Câu Ý Đáp án Điểm 1 0,5
(x + y)2 = x2 + 2xy + y2 7 1 điểm 2 0,5 2 x − 25 = (x – 5)(x + 5) 1 3 2 2 ( 5x y - x y + xy) : xy 2 − + = 5x y 3x 1 0,5 2 Ta có: A + 2M = P A = P - 2M 3 2
A = 3x - 2x y - xy + 3 - 2 ( 3 2 x - x y + 2xy + 3) 0,25 8 2 điểm 0,25 3 2 3 2
A = 3x - 2x y - 2xy + 3 - 2x + 2x y - 4xy - 6 3 A = x - 6xy - 3 0,25 3 2 N = (3x - ) 2 0,25 2 æ ö 2 4 ç ÷ 0,25 N = 3 ç . - 2÷ = ç ÷ (4 - ) 2 ç 3 ÷ è ø 0,25 2 N = 2 = 4 HS vẽ đúng hình A 9 E 0,25 F 3 điểm H B G M C I K BH ⊥ AC Ta có   ∥ ( ) BH KC 1 0,5 KC ⊥ AC a CH  ⊥ AB Và   0,5 CH ∥ KB (2) KB ⊥ AB 0,25 Từ ( )
1 , (2)  BHCK là hình bình hành. b
Vì BHCK là hình bình hành nên BC cắt HK tại trung điểm M của BC 0,25
 M là trung điểm của HK  H, M , K thẳng hàng. 0,25
ΔBHI có BG vừa là đường cao, trung tuyến nên BG là trung trực của HI . Khi đó MH = MI 1
ΔHIK có IM là đường trung tuyến và IM = HK  ΔHIK vuông tại I 0,25 2 c
 IK ⊥ HI . Mà BC ⊥ HI  BC∥IK  BCKI là hình thang. 0,25 ΔBIH cân tại 0,25
B lại có BG là trung trực nên là phân giác HBI  GBI = GBH
Mà HBG = GCK (so le trong)  IBC = KCB  BCKI là hình thang cân. 0,25 C = ( 2 x - ) 1 ( 2 x + ) 1 ( 4 x + ) 1 ( 8 x + ) 1 ( 16 x + ) 1 ( 32 x + ) 64 1 - x 0,25 C = ( 4 x - ) 1 ( 4 x + ) 1 ( 8 x + ) 1 ( 16 x + ) 1 ( 32 x + ) 64 1 - x C = ( 8 x - ) 1 ( 8 x + ) 1 ( 16 x + ) 1 ( 32 x + ) 64 1 - x 10 0,25 16 16 32 64 1 điểm C = (x - ) 1 (x + ) 1 (x + ) 1 - x C = ( 32 x - ) 1 ( 32 x + ) 64 1 - x 0,25 64 64 C = x - 1 - x C = -1 Ï x 0,25
Chú ý: Học sinh làm cách khác, nếu đúng vẫn cho điểm tối đa.