Đề thi giữa học kì 1 Toán 7 năm 2020 – 2021 trường THCS Archimedes Academy – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề thi giữa học kì 1 Toán 7 năm 2020 – 2021 trường THCS Archimedes Academy – Hà Nội; đề thi có đáp án và lời giải chi tiết.

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 7

Môn: Toán 7

Thông tin:

5 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
THCS ARCHIMEDES ACADEMY
THCS.TOANMATH.com
Câu 1. (2,0 điểm) Tính:
a)
33
0,5
16 4
−
+−
; b)
( )
0
2 13
2 0,75
3 32

− − ++


;
c)
5 5 3 1 11
:
4 6 8 6 12

− −+


; d)
32
22 1
: 1 : 1, 5
33 2
 
+−
 
 
Câu 2. (2,0 điểm) Tìm
,,xyz
biết:
a)
23xy=
và
54xy =
; b)
856
xyz
= =
và
Câu 3. (2,0 điểm) Hưởng ứng phong trào khuyên góp sách, ba lớp
1
7A
,
23
7 ,7AA
đã khuyên góp
được tổng số 180 cuốn sách. Biết số cuốn sách của 3 lớp
123
7 ,7 ,7AAA
tỉ lệ với các số
5;6; 4
. Tính số sách mà mỗi lớp đã khuyên góp được.
Câu 4. (3,5 điểm) Vẽ lại hình và chú thích đầy đủ
Cho hình vẽ. Biết
62 ; 118 ; 152MNb NMa QPb=° =°=°
a ) Chứng minh
'// 'aa bb
;
b) Tính số đo góc
MQP
. Trên nữa mặt phẳng bờ
'aa
chứa điểm
N
, vẽ tia
//Mx QP
.
Tính số đo góc
aMx
;
c) Trên nữa mặt phẳng bờ
'aa
không chứa điểm
N
vẽ tia
'Mx
sao cho
''aMx a Mx=
.
Chứng minh hai tia
Mx
và
'Mx
là hai tia đối nhau.
Câu 5. (0,5 điểm) Học sinh chỉ chọn một trong hai ý sau :
a ) Cho các số
,,abc
thỏa mãn
.. 0abc≠
và
111 1
3
abbc ca
abc c a b
+++
++= + + =
.
Tính
2020.S abc=++=
b) Tìm các số
,,abc
nguyên dương thỏa mãn:
32
3 55
b
aa+ +=
và
35
c
a +=
HẾT
152
°
118
°
62
°
b b'
a a'
Q
M
N
P
ĐỀ THI GIỮA HỌC KÌ I
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 7
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
-----------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. (2,0 điểm) Tính:
a)
33
0,5
16 4
−
+−
; b)
( )
0
2 13
2 0,75
3 32

− − ++


;
c)
5 5 3 1 11
:
4 6 8 6 12

− −+


; d)
32
22 1
: 1 : 1, 5
33 2
 
+−
 
 
Lời giải
a)
33
0,5
16 4
−
+−
8 3 12
16 16 16
=++
11 12
16 16
= +
23
16
=
.
b)
( )
0
2 13
2 0,75
3 32

− − ++


=
2 61 3
1
3 33 2

− − ++


253
1
332
=−++
33
1
32
−
= ++
3
11
2
=−+ +
( )
3
11
2
=−+ +
3
0
2
= +
3
2
=
.
c)
5 5 3 1 11
:
4 6 8 6 12

− −+


5 5 9 4 11
:
4 6 24 24 12

=− −+


5 5 24 11
.
4 6 5 12
=−+
5 11
4
4 12
= −+
15 48 11
12 12 12
=−+
33 11
12 12
−
= +
22
12
−
=
11
6
−
=
.
d)
32
22 1
: 1 :1, 5
33 2

+−


2 33
:
3 22
−
= +
2 32
.
3 23
−
= +
2
1
3
= −
23
33
= −
1
3
−
=
Câu 2. (2,0 điểm) Tìm
,,xyz
biết:
a)
23xy=
và
54xy =
; b)
856
xyz
= =
và
Lời giải
a) Ta có:
23xy=
3
2
xy⇒=
. Thay
3
2
xy=
vào
54xy =
ta được:
3
. 54
2
yy=
2
3
54:
2
y⇒=
2
36y⇒=
6
6
y
y
=
⇒
= −
Với
6y =
ta có
3
.6 9
2
x = =
Với
6y = −
ta có
( )
3
.6 9
2
x = −=−
THCS ARCHIMEDES ACADEMY
THCS.TOANMATH.com
ĐỀ THI GIỮA HỌC KÌ I
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 7
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
-----------------------------------------
Vậy cặp giá trị
( )
;xy
cần tìm là
( )
9;6
và
( )
9; 6−−
b)
856
xyz
= =
và
2 30xyz+−=−
Theo bài ra ta có:
2 30
2
8 5 6 2.8 5 6 15
x y z xyz+− −
= = = = = −
+−
(áp dụng tính chất dãy tỉ số bằng
nhau)
Khi đó ta có:
2
8
x
= −
2.8x⇒=−
16x⇒=−
2
5
y
= −
2.5y⇒=−
10y⇒=−
2
6
z
= −
2.6z⇒=−
12z⇒=−
Vậy
16; 10; 12xyz=−=−=−
.
Câu 3. (2,0 điểm) Hưởng ứng phong trào khuyên góp sách, ba lớp
1
7A
,
23
7 ,7AA
đã khuyên góp
được tổng số 180 cuốn sách. Biết số cuốn sách của 3 lớp
123
7 ,7 ,7AAA
tỉ lệ với các số
5;6; 4
. Tính số sách mà mỗi lớp đã khuyên góp được.
Lời giải
Gọi số sách mà ba lớp
7 ,7 ,7ABC
khuyên góp được lần lượt là
;;xyz
(
*
;;xyz∈
)
Vì số cuốn sách của 3 lớp
123
7 ,7 ,7AAA
tỉ lệ với các số
5;6; 4
ta có:
564
xyz
= =
.
Vì đã khuyên góp được tổng số 180 cuốn sách nên :
180xyz++=
Ta có:
180
12
564564 15
x y z xyz++
= = = = =
++
(áp dụng tính chất dãy tỉ số bằng nhau)
Khi đó ta có:
12
5
x
=
12.5x⇒=
60x⇒=
(TM)
12
6
y
=
12.6y⇒=
72y⇒=
(TM)
12
4
z
=
12.4z⇒=
48z⇒=
(TM)
Vậy số sách mà ba lớp
7 ,7 ,7ABC
khuyên góp được lần lượt là
60;72;48
cuốn sách.
Câu 4. (3,5 điểm) Vẽ lại hình và chú thích đầy đủ
Cho hình vẽ. Biết
62 ; 118 ; 152MNb NMa QPb=° =°=°
a ) Chứng minh
'// 'aa bb
;
b) Tính số đo góc
MQP
. Trên nữa mặt phẳng bờ
'aa
chứa điểm
N
, vẽ tia
//Mx QP
.
Tính số đo góc
aMx
;
c) Trên nữa mặt phẳng bờ
'aa
không chứa điểm
N
vẽ tia
'Mx
sao cho
''aMx a Mx=
.
Chứng minh hai tia
Mx
và
'Mx
là hai tia đối nhau.
Lời giải
a.
Vì
62 118 180MNb NMa+ = °+ °= °
mà hai góc này ở vị
trí trong cùng phía nên
'// 'aa bb
(dấu hiệu nhận biết)
b. Ta có :
180 180 28QPb QPN QPN QPb+ = °⇒ = °− = °
(hai góc
bù nhau)
Ta có :
28 62 90MQP QPN QNP= + = °+ °= °
(tính chất góc ngoài tam giác)
Vì
//Mx QP
và
90
o
MQP =
suy ra
90
o
xMQ =
(quan hệ song song và vuông góc)
Từ đó :
00
118 118 90 28
oo
aMx xMQ= − = −=
c. Ta có :
0 00
' 180 ' ' 180 ' ' 180aMx xMa aMx x Ma x Mx+ =⇒+ =⇒ =
hay Mx và Mx’ là
hai tia đối nhau.
Câu 5. (0,5 điểm) Học sinh chỉ chọn một trong hai ý sau :
a ) Cho các số
,,abc
thỏa mãn
.. 0abc≠
và
111 1
3
abbc ca
abc c a b
+++
++= + + =
.
Tính
2020.S abc=+++
b) Tìm các số
,,abc
nguyên dương thỏa mãn:
32
3 55
b
aa+ +=
và
35
c
a +=
Lời giải
a.
Ta có:
1
3
abbc ca
cab
+⇒
+++
+=
1
1 1 13
3
ab bc ca
cab
+++
⇔ ++ ++ += +
10
3
abc abc abc
cab
++ ++ ++
⇔++=
( )
1 1 1 10
3
abc
abc

⇔ ++ + + =


( )
1 10
.
33
abc⇔ ++ =
10abc⇔++=
Thay vào ta có:
10 2020 2030.S =+=
b. Tìm các số
,,abc
nguyên dương thỏa mãn:
32
3 55
b
aa+ +=
(1) và
35
c
a +=
(2)
Ta có:
32
3 55
b
aa+ +=⇔
( )
2
3 55
b
aa⇔ + +=
2
.5 5 5
cb
a⇔ +=
(3)
Xét:
TH1:
1c =
thay vào (2) ta có
2a =
, khi đó thay tiếp vào (1) ta được
2b =
.
TH2:
1c >
khi đó từ (3) suy ra
1b >
nhưng sẽ vô lý vì cả
2
.5 ; .5.
cb
a
đều chia hết cho 5
2
mà 5 thì không.
Vậy
2; 2; 1abc= = =
.
__________ THCS.TOANMATH.com __________
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THCS ARCHIMEDES ACADEMY
ĐỀ THI GIỮA HỌC KÌ I NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 7
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
----------------------------------------- Câu 1. (2,0 điểm) Tính: 3 3 − 2  1  3 a) 0, 5 + − ; b) − 2 − + +   (0,75)0 ; 16 4 3  3  2 3 2 5 5  3 1  11  2   2   1  c) − : − +   ; d) : + 1 − :1, 5       4 6  8 6  12  3   3   2  Câu 2.
(2,0 điểm) Tìm x, y, z biết: x y z
a) 2x = 3y và xy = 54 ; b) =
= và 2x + y − z = 30 − 8 5 6 Câu 3.
(2,0 điểm) Hưởng ứng phong trào khuyên góp sách, ba lớp 7A , 7A ,7A đã khuyên góp 1 2 3
được tổng số 180 cuốn sách. Biết số cuốn sách của 3 lớp 7A ,7A ,7A tỉ lệ với các số 1 2 3
5; 6; 4 . Tính số sách mà mỗi lớp đã khuyên góp được. Câu 4.
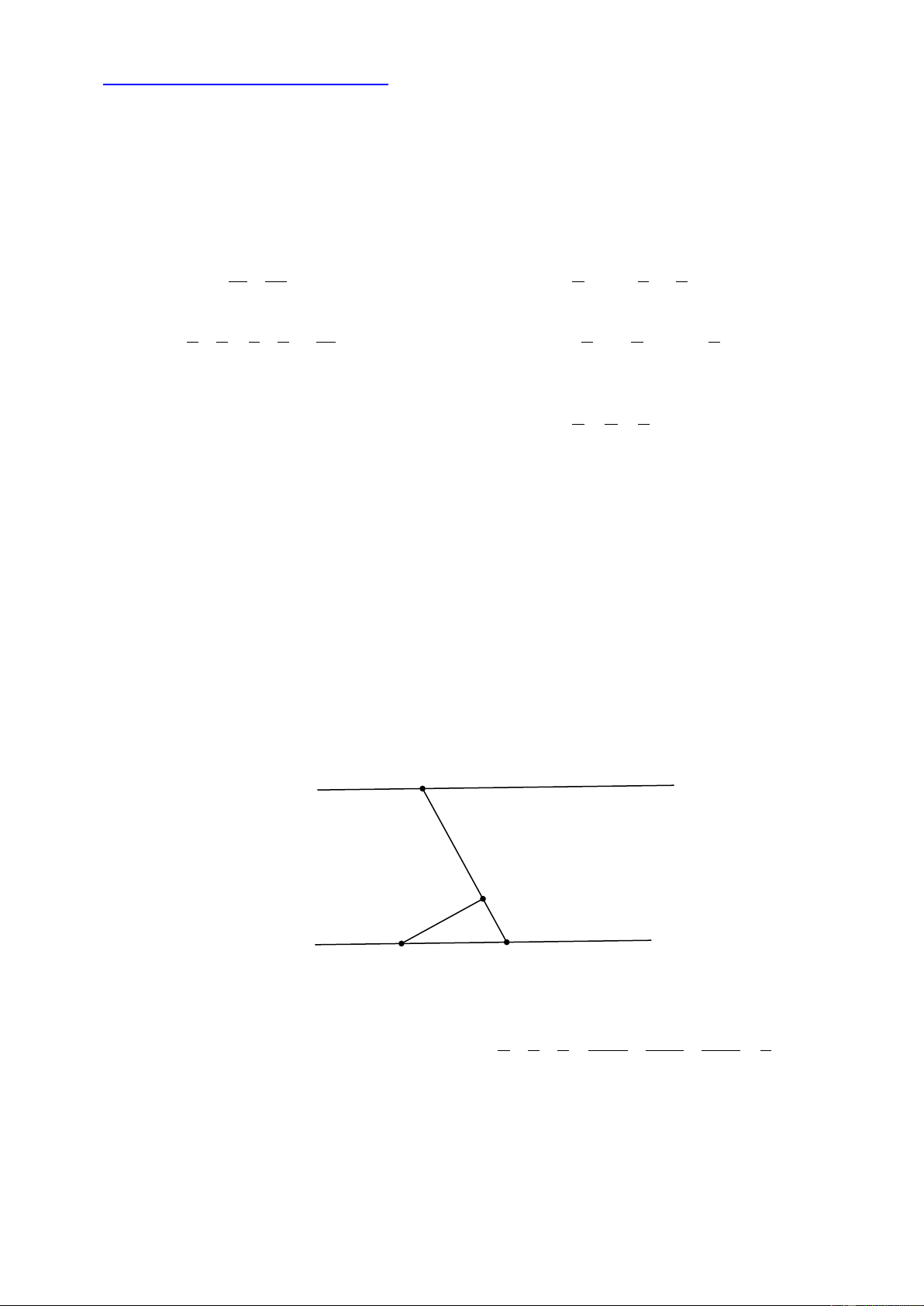
(3,5 điểm) Vẽ lại hình và chú thích đầy đủ Cho hình vẽ. Biết  MNb = 62°  ; NMa = 118°  ;QPb = 152°
a ) Chứng minh aa ' // bb ' ;
b) Tính số đo góc MQP . Trên nữa mặt phẳng bờ aa ' chứa điểm N , vẽ tia Mx// QP .
Tính số đo góc aMx ;
c) Trên nữa mặt phẳng bờ aa ' không chứa điểm N vẽ tia Mx ' sao cho  aMx = a ' Mx ' .
Chứng minh hai tia Mx và Mx ' là hai tia đối nhau. a M a' 118° Q 152° 62° b P N b' Câu 5.
(0,5 điểm) Học sinh chỉ chọn một trong hai ý sau : 1 1 1 a + b b + c c + a 1
a ) Cho các số a,b, c thỏa mãn . a . b c ≠ 0 và + + = + + = . a b c c a b 3
Tính S = a + b + c = 2020.
b) Tìm các số a,b, c nguyên dương thỏa mãn: 3 2 + 3 + 5 = 5b a a và 3 5c a + =  HẾT THCS ARCHIMEDES ACADEMY
ĐỀ THI GIỮA HỌC KÌ I NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 7
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
-----------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. (2,0 điểm) Tính: 3 3 − 2  1  3 a) 0, 5 + − ; b) − 2 − + +   (0,75)0 ; 16 4 3  3  2 3 2 5 5  3 1  11  2   2   1  c) − : − +   ; d) : + 1 − :1, 5       4 6  8 6  12  3   3   2  Lời giải 3 3 − a) 0, 5 + − 8 3 12 = + + 11 12 = + 23 = . 16 4 16 16 16 16 16 16 2  1  3 2  6 1  3 2 5 3 − b) − 2 − + +   (0,75)0 = − − + +1   = − + + 3 3 1 = + + 3 1 = 1 − + +1 3  3  2 3  3 3  2 3 3 2 3 2 2 = (− + ) 3 1 1 + 3 = 0 + 3 = . 2 2 2 5 5  3 1  11 5 5  9 4  11 5 5 5 11 c) − : − +   = − : − +   = − : + 5 5 24 11 = − . + 4 6  8 6  12 4 6  24 24  12 4 6 24 12 4 6 5 12 5 11 = − 4 + 4 12 15 48 11 − − − = − + 33 11 = + 22 = 11 = . 12 12 12 12 12 12 6 3 2  2   2   1  2 3 − 3 − − d) : + 1 − :1, 5       = + 2 3 2 : = + 2 . = − 2 3 1 = − 1 =  3   3   2  3 2 2 3 2 3 3 3 3 3 Câu 2.
(2,0 điểm) Tìm x, y, z biết: x y z
a) 2x = 3y và xy = 54 ; b) =
= và 2x + y − z = 30 − 8 5 6 Lời giải 3 a) Ta có: 2x = 3 3y ⇒ x = y . Thay x =
y vào xy = 54 ta được: 2 2 3 3  y = . y y = 54 2 ⇒ y = 54 : 2 ⇒ y = 6 36 ⇒  2 2  y = 6 − 3 Với y = 6 = ta có x = .6 9 2 3 Với y = 6 − − = − ta có x = .( 6) 9 2 Vậy cặp giá trị ( ;
x y ) cần tìm là (9;6) và ( 9; − 6 − ) x y z b)
= = và 2x + y − z = 30 − 8 5 6 x y z
2x + y − z 30 − Theo bài ra ta có: = = = = = 2
− (áp dụng tính chất dãy tỉ số bằng 8 5 6 2.8 + 5 − 6 15 nhau) Khi đó ta có: x = 2 − ⇒ x = 2.8 − ⇒ x = 16 − 8 y = 2 − ⇒ y = 2.5 − ⇒ y = 10 − 5 z = 2 − ⇒ z = 2.6 − ⇒ z = 12 − 6 Vậy x = 16 − ; y = 10 − ; z = 12 − . Câu 3.
(2,0 điểm) Hưởng ứng phong trào khuyên góp sách, ba lớp 7A , 7A ,7A đã khuyên góp 1 2 3
được tổng số 180 cuốn sách. Biết số cuốn sách của 3 lớp 7A ,7A ,7A tỉ lệ với các số 1 2 3
5; 6; 4 . Tính số sách mà mỗi lớp đã khuyên góp được. Lời giải
Gọi số sách mà ba lớp 7 ,
A 7B, 7C khuyên góp được lần lượt là ; x y; z ( * ;
x y; z ∈  ) x y z
Vì số cuốn sách của 3 lớp 7 A , 7 A , 7 A tỉ lệ với các số 5;6; 4 ta có: = = . 1 2 3 5 6 4
Vì đã khuyên góp được tổng số 180 cuốn sách nên : x + y + z = 180 x y z x + y + z 180 Ta có: = = = =
= 12 (áp dụng tính chất dãy tỉ số bằng nhau) 5 6 4 5 + 6 + 4 15 Khi đó ta có:
x =12 ⇒ x =12.5 ⇒ x = 60 (TM) 5
y =12 ⇒ y =12.6 ⇒ y = 72 (TM) 6
z =12 ⇒ z =12.4 ⇒ z = 48 (TM) 4
Vậy số sách mà ba lớp 7 ,
A 7B, 7C khuyên góp được lần lượt là 60; 72; 48 cuốn sách. Câu 4.
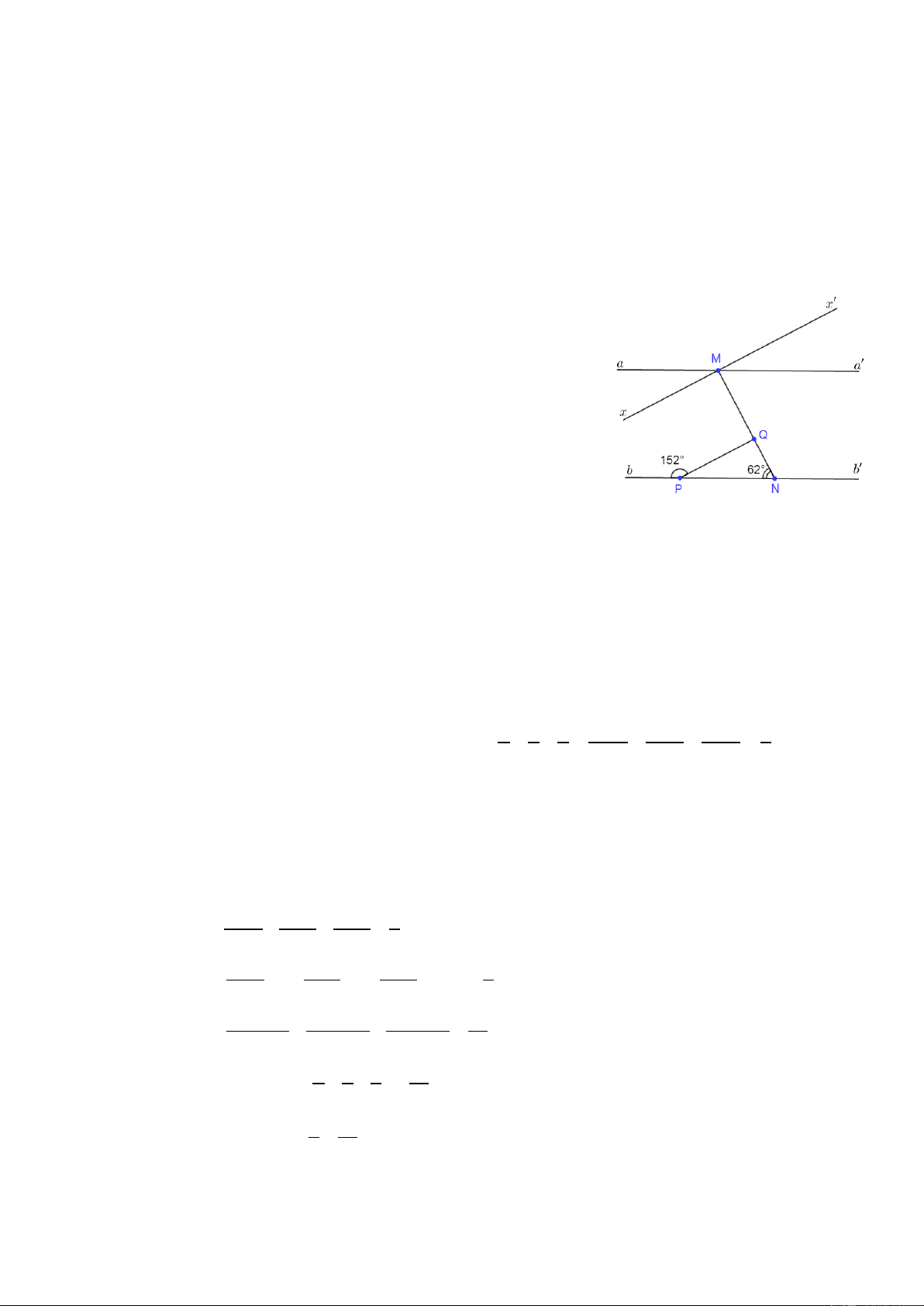
(3,5 điểm) Vẽ lại hình và chú thích đầy đủ Cho hình vẽ. Biết  MNb = 62°  ; NMa = 118°  ;QPb = 152°
a ) Chứng minh aa ' // bb ' ;
b) Tính số đo góc MQP . Trên nữa mặt phẳng bờ aa ' chứa điểm N , vẽ tia Mx// QP .
Tính số đo góc aMx ;
c) Trên nữa mặt phẳng bờ aa ' không chứa điểm N vẽ tia Mx ' sao cho  aMx = a ' Mx ' .
Chứng minh hai tia Mx và Mx ' là hai tia đối nhau. Lời giải a. Vì  MNb +
NMa = 62° +118° = 180° mà hai góc này ở vị
trí trong cùng phía nên aa ' // bb ' (dấu hiệu nhận biết) b. Ta có :  QPb + QPN = 180° ⇒ QPN = 180° − QPb = 28° (hai góc bù nhau) Ta có :  MQP =  QPN +
QNP = 28° + 62° = 90° (tính chất góc ngoài tam giác)
Vì Mx// QP và  90o MQP = suy ra  90o xMQ =
(quan hệ song song và vuông góc) Từ đó :  0 = − 0 118
=118 − 90o = 28o aMx xMQ c. Ta có :  aMx + 0 xMa = ⇒  aMx  0 + x Ma = ⇒ 0 ' 180 ' ' 180
x ' Mx ' = 180 hay Mx và Mx’ là hai tia đối nhau. Câu 5.
(0,5 điểm) Học sinh chỉ chọn một trong hai ý sau : 1 1 1 a + b b + c c + a 1
a ) Cho các số a,b, c thỏa mãn . a . b c ≠ 0 và + + = + + = . a b c c a b 3
Tính S = a + b + c + 2020.
b) Tìm các số a,b, c nguyên dương thỏa mãn: 3 2 + 3 + 5 = 5b a a và 3 5c a + = Lời giải a. Ta có: a + b b + c c + a 1 ⇒ + + = c a b 3 a + b b + c c + a 1 ⇔ +1+ +1+ +1 = 3 + c a b 3 a + b + c a + b + c a + b + c 10 ⇔ + + = c a b 3 (  
⇔ a + b + c) 1 1 1 10 + + =    a b c  3
⇔ (a + b + c) 1 10 . = 3 3
⇔ a + b + c =10
Thay vào ta có: S = 10 + 2020 = 2030.
b. Tìm các số a,b, c nguyên dương thỏa mãn: 3 2 + 3 + 5 = 5b a a (1) và 3 5c a + = (2) Ta có: 3 2 ⇔ + 3 + 5 = 5b a a 2 ⇔ ( +3)+5 = 5b a a 2 ⇔ .5c + 5 = 5b a (3) Xét:
TH1: c = 1 thay vào (2) ta có a = 2 , khi đó thay tiếp vào (1) ta được b = 2 .
TH2: c > 1 khi đó từ (3) suy ra b > 1 nhưng sẽ vô lý vì cả 2.5c; . . 5b a đều chia hết cho 52 mà 5 thì không.
Vậy a = 2;b = 2;c = 1 .
__________ THCS.TOANMATH.com __________