TRƯỜNG THCS NGÔ SĨ LIÊN
ĐỀ THI GIỮA HỌC KÌ I NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 8
Thời gian làm bài: 60 phút (không kể thời gian phát đề) Câu 1: (1,5 điểm). Cho hai biểu thức 2
A = x − x + 5 và B = (x −1)(x + 2) − x(x − 2) − 3x
a) Tính giá trị của biểu thức A khi x = 2
b) Chứng tỏ rằng B = 2
− với mọi giá trị của biến x .
c) Tìm giá trị nhỏ nhất của biểu thức C = A + . B Câu 2: (2,0 điểm).
Phân tích đa thức thành nhân tử: a) 2 x − 8x b) 2
x − xy − 6x + 6 y . c) 2 2
x − 6x + 9 − y . d) 3 3
x + y + 2x + 2 y Câu 3: (1,5 điểm)
Tìm các số thực x, biết : a) ( x − )2 2 3 − 49 = 0.
b) 2x(x − 5) − 7(5 − x) = 0 c) 2
x − 3x −10 = 0 Câu 4: (1,0 điểm)
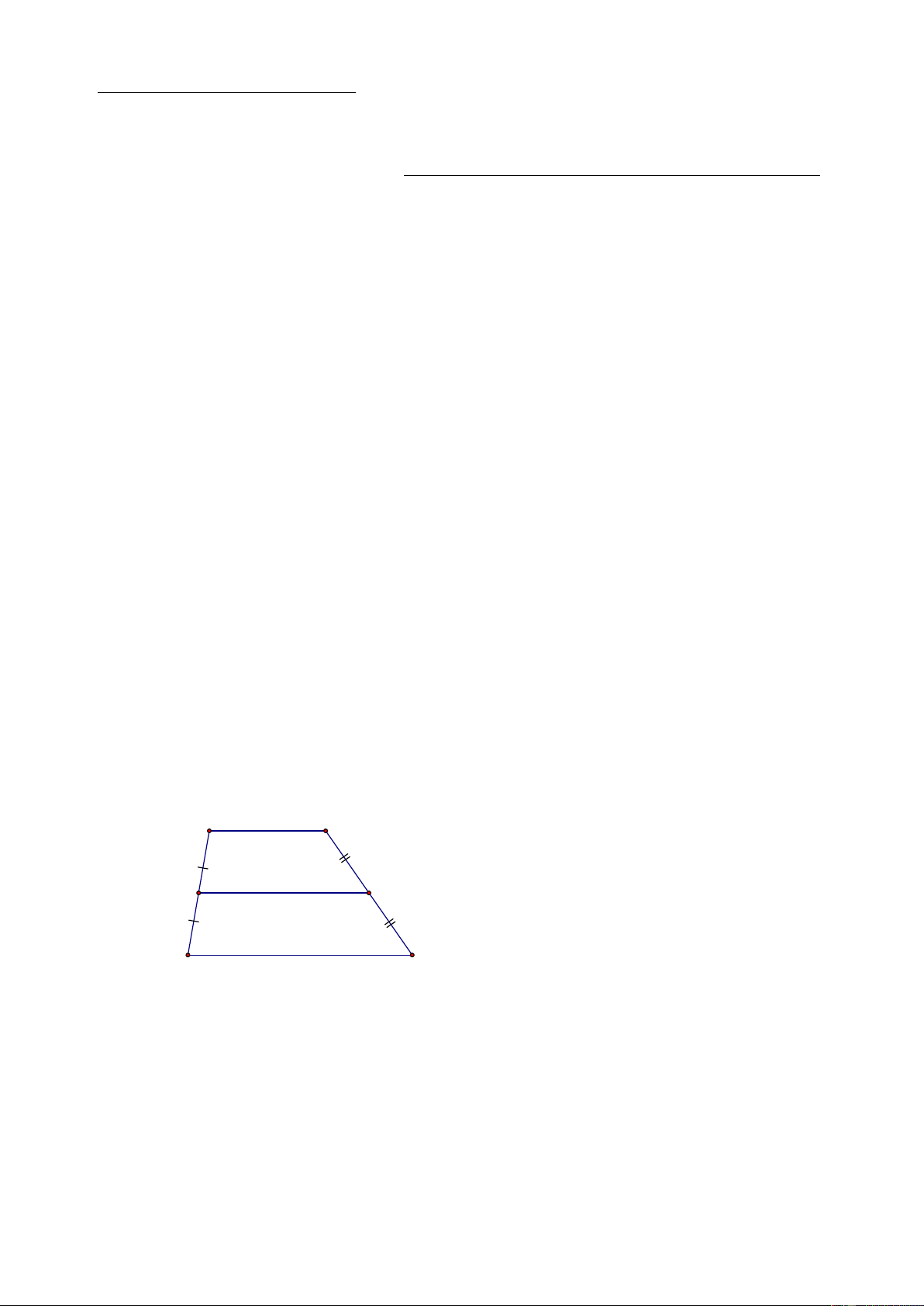
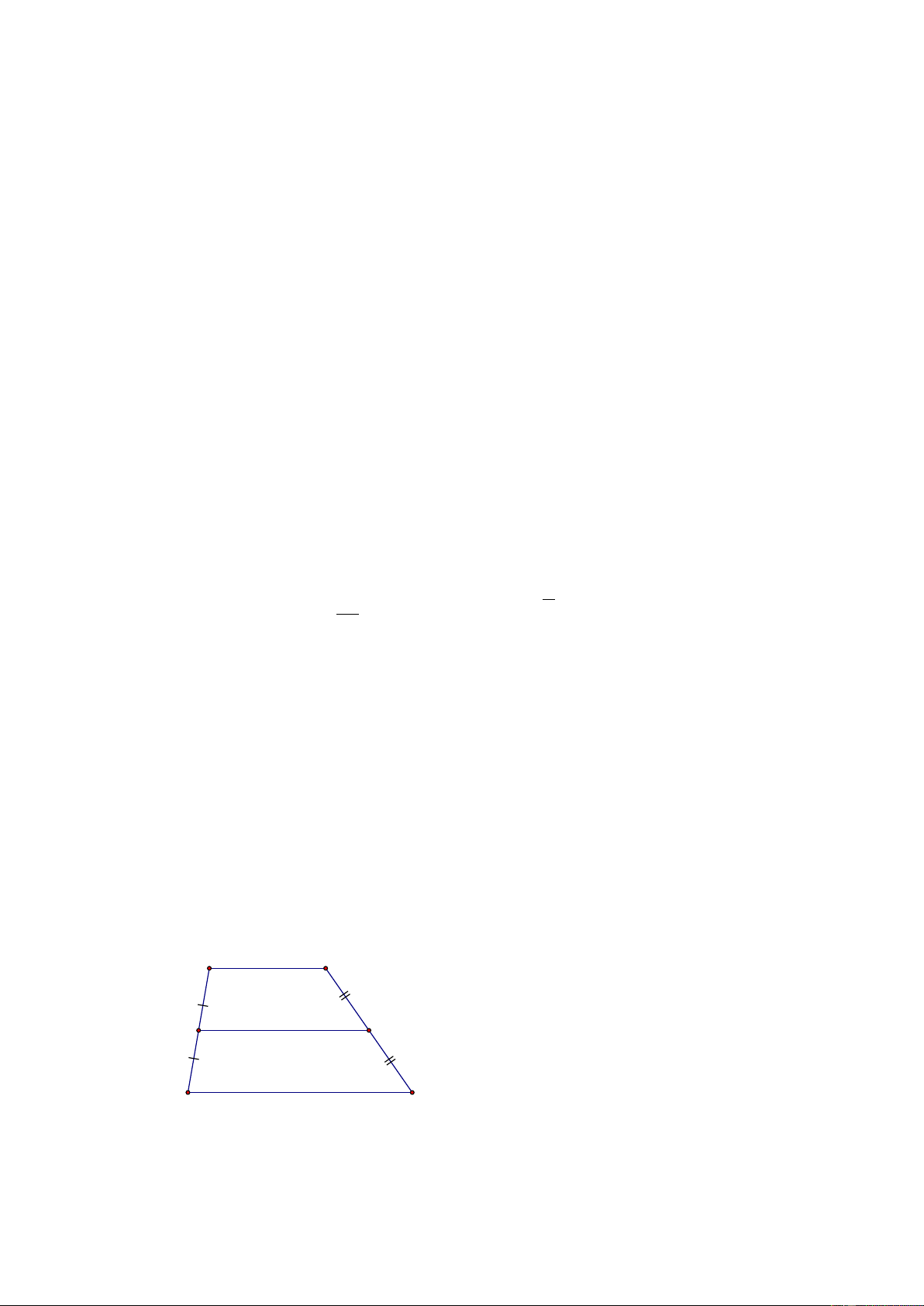
Cho hình vẽ bên, biết AB//CD , AB = 5cm , CD = 7 cm . Tính EG . A B G E D C Câu 5: (3,5 điểm) Cho A
∆ BC có E là trung điểm của AC . Qua E kẻ ED// AB(D ∈ BC);
EF // BC( F ∈ AB)
a) Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC .
b) Gọi H là điểm đối xứng của D qua F . Chứng minh rằng HB// AD .
c) Gọi I là trung điểm của HB ; K là giao điểm của AD và EF . Chứng minh rằng
I , K , E thẳng hàng. AB d) A
∆ BC cần có thêm điều kiện gì để HF = . 2 Câu 6: (0,5 điểm) Tìm các cặp số ( ;
x y ) biết : 4 2 2
y + y + x − 8 y − 4x + 2xy + 7 = 0 HẾT
TRƯỜNG THCS NGÔ SĨ LIÊN
ĐỀ THI GIỮA HỌC KÌ I NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 8
Thời gian làm bài: 60 phút (không kể thời gian phát đề) Câu 1: (1,5 điểm). Cho hai biểu thức 2
A = x − x + 5 và B = (x −1)(x + 2) − x(x − 2) − 3x
a) Tính giá trị của biểu thức A khi x = 2
b) Chứng tỏ rằng B = 2
− với mọi giá trị của biến x .
c) Tìm giá trị nhỏ nhất của biểu thức C = A + . B Lời giải
a) Thay x = 2 vào biểu thức A Tính được 2 A = 2 − 2 + 5 = 7 b)
B = (x −1)(x + 2) − x(x − 2) − 3x 2 2
B = x + 2x − x − 2 − x + 2x − 3x B = 2 − c) Ta có 2 2
C = x − x + 5 − 2 = x − x + 3 2  1  11 C = x − +    2  4 11 1
Giá trị nhỏ nhất của biểu thức C là tại x = 4 2 Câu 2: (2,0 điểm).
Phân tích đa thức thành nhân tử : a) 2 x − 8x b) 2
x − xy − 6x + 6 y . c) 2 2
x − 6x + 9 − y . d) 3 3
x + y + 2x + 2 y Lời giải a) 2
x − 8x = x(x − 8) b) 2
x − xy − 6x + 6 y 2
= (x − xy) − (6x − 6y) = x(x − y) − 6(x − y) = (x − 6)(x − y) 2 c) . 2 2
x − 6x + 9 − y . = ( 2 x − x + ) 2 6
9 − y = ( x − ) 2 3
− y = (x −3− y)(x −3+ y) d) 3 3
x + y + 2x + 2 y = ( 3 3
x + y ) + (2x + 2y) = (x + y)( 2 2
x − xy + y ) + 2( x + y) = ( x + y)( 2 2
x − xy + y + 2) Câu 3: (1,5 điểm)
Tìm các số thực x, biết : a) ( x − )2 2 3 − 49 = 0.
b) 2x(x − 5) − 7(5 − x) = 0 c) 2
x − 3x −10 = 0 Lời giải a) ( x − )2 2 3 − 49 = 0. ⇔ ( x − )2 2 2 3 − 7 = 0
⇔ (2x − 3− 7)(2x − 3+ 7) = 0
⇔ (2x −10)(2x + 4) = 0 2x −10 = 0 x = 5 ⇔ ⇔   2x + 4 = 0 x = 2 −
Vậy x = 5 ; x = 2 −
b) 2x(x − 5) − 7(5 − x) = 0
⇔ 2x(x − 5) + 7(x − 5) = 0
⇔ (x − 5)(2x + 7) = 0 x = 5 x − 5 = 0  ⇔ ⇔ 7  7 − x = ; x = − 2x + 7 = 0 x = Vậy 5 2  2 c) 2
x − 3x −10 = 0 2
⇔ x − 5x + 2x −10 = 0
⇔ x(x − 5) + 2(x − 5) = 0
⇔ (x − 5)(x + 2) = 0 x − 5 = 0 x = 5 ⇔ ⇔   x + 2 = 0 x = 2 −
Vậy x = 5 ; x = 2 −
Câu 4: (1 điểm) (Không phải vẽ lại hình).
Cho hình vẽ bên, biết AB // CD , AB = 5cm , CD = 7 cm . Tính EG . A B G E D C Lời giải
Ta có AB // CD (gt) nên tứ giác ABCD là hình thang.
Mà E, G lần lượt là trung điểm của AD, BC (gt)
Suy ra EG là đường trung bình của hình thang ABCD . AB + CD 5 + 7 ⇒ EG = = = 6cm . 2 2
Câu 5: (3,5 điểm). Cho A
∆ BC có E là trung điểm của AC . Qua E kẻ ED // AB(D ∈ BC) ;
EF // BC ( F ∈ AB)
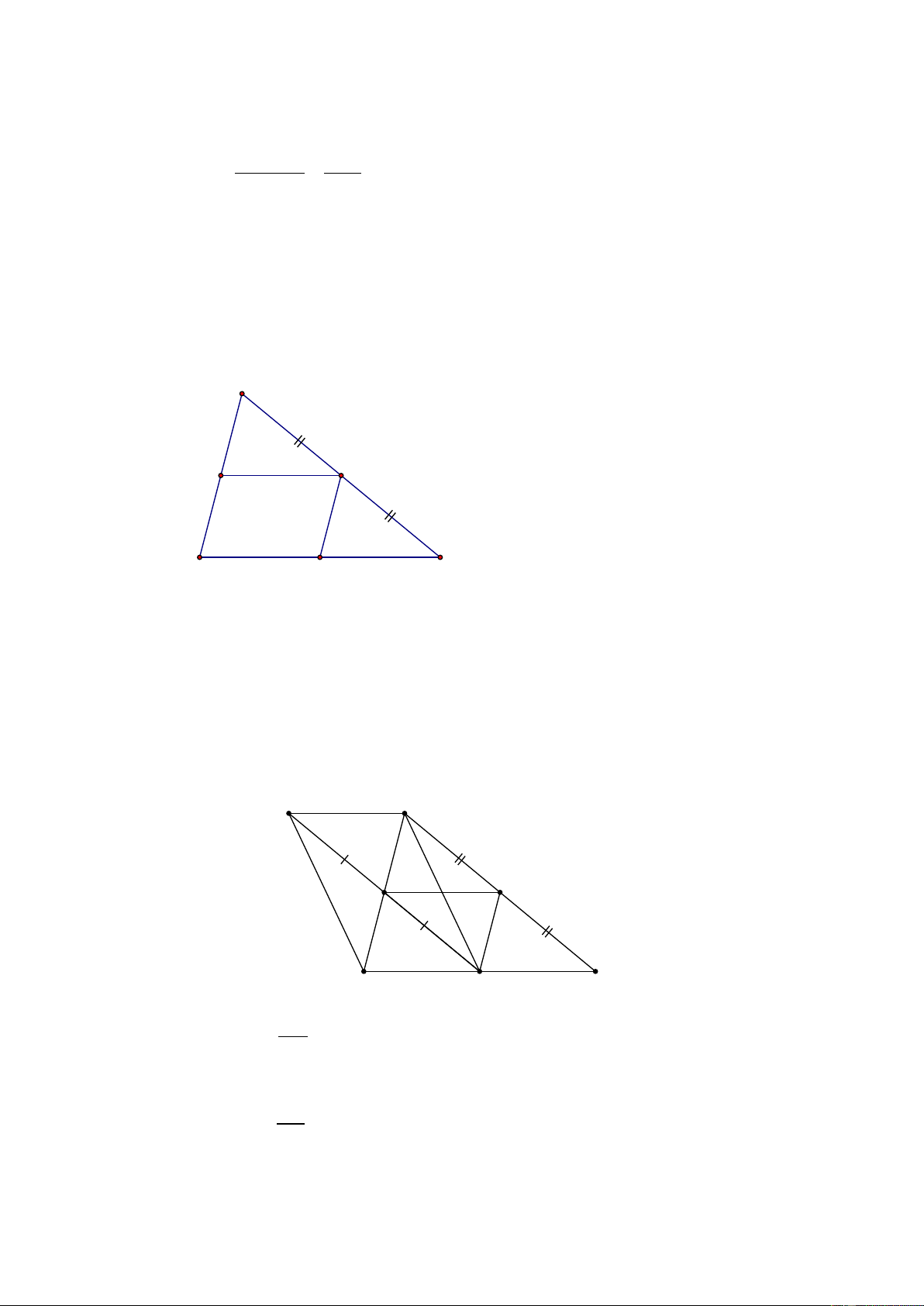
a) Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC . Lời giải A E F B D C
a) + Xét tứ giác BDEF có: EF // BD (vì EF // BC - gt) ED // BF (vì ED // AB - gt)
⇒ BDEF là hình bình hành (DHNB). + Xét A
∆ BC có: E là trung điểm của AC và ED // BF
Suy ra D là trung điểm của đoạn thẳng BC (định lý đường trung bình trong tam giác). b) H A E F B D C AC Vì AE = EC = 2 Và EF // BC AB ⇒ AF = FB = 2
Ta có : AB ∩ HD = {F} , mà F là trung điểm của AB và HD
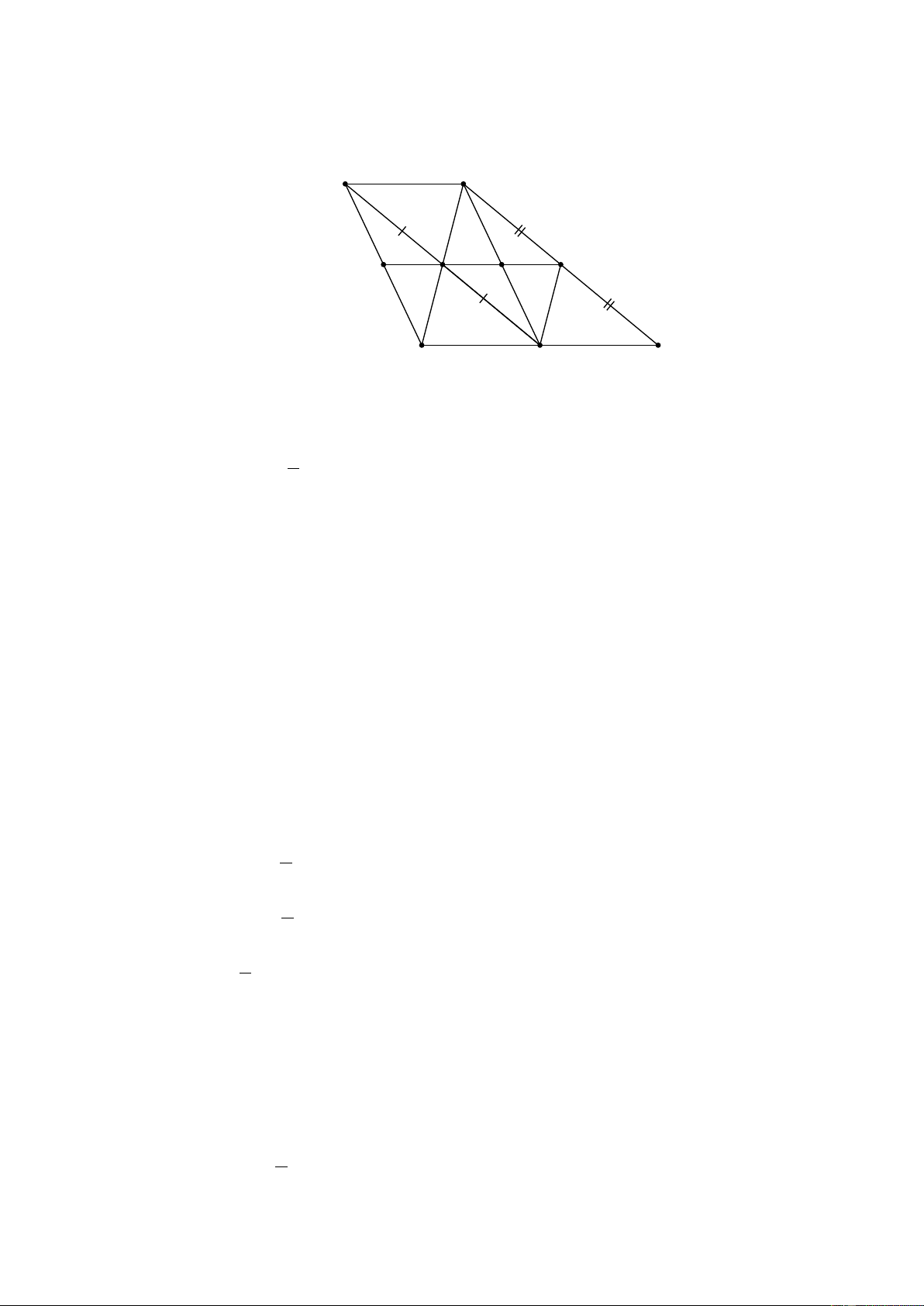
⇒ tứ giác AHBD là hình bình hành ⇒ HB // AD (đpcm). c) H A F E I K B D C
Ta có: FD là đường trung bình của A ∆ BC FD // AC  ⇒  1 FD = AE = AC  2
⇒ tứ giác FDEA là hình bình hành.
FD ∩ EF = {K} (gt) ⇒ K là trung điểm của AD .
Và I là trung điểm của HB .
⇒ IK là đường trung bình của hình bình hành AHBD .
⇒ IK // BD . (1)
Tương tự: I là trung điểm của HB
E là trung điểm của AC
⇒ IE là đường trung bình của hình thang AHBC
⇒ IE // BC ⇒ IE // BD (2)
Từ (1) và (2) ⇒ I , K , E thẳng hàng. (dpcm)
d) Xét hình bình hành AHBD có: AB ∩ HD = {F} 1
⇒ HF = FD = HD 2 1 Và AF = FB = AB 2 Để 1 HF =
AB ⇒ HD = AB 2
Hình bình hành AHBD có hai đường chéo HD và AB bằng nhau
⇒ AHBD là hình chữ nhật ⇒ AD ⊥ BD ⇒ AD là đường cao của A ∆ BC
Mặt khác, D là trung điểm của BC (theo cm câu a) ⇒ AD là đường trung tuyến của A ∆ BC A
∆ BC có AD vừa là đường cao, vừa là trung tuyến ⇒ A
∆ BC cân tại A . 1 Vậy, để HF = AB thì A
∆ BC phải cân tại A 2 Câu 6: (0,5 điểm) Tìm các cặp số ( ; x y ) biết: 4 2 2
y + y + x − 8 y − 4x + 2xy + 7 = 0 Lời giải 4 2 2
y + y + x − 8 y − 4x + 2xy + 7 = 0 4 2
⇔ y − 2y +1+ 2( 2 y − 2 y + ) 2 2
1 + x + y + 4 + 2xy − 4x − 4 y = 0 2 2 2 2
⇔ (y −1) + 2(y −1) + (x + y − 2) = 0 NX: 2 2 ( y −1) ≥ 0 ; 2 2( y −1) ≥ 0 ; 2
(x + y − 2) ≥ 0 2 y =1 Dấu “=” xảy ra ⇔   y = 1 ⇔ x = y = 1. x + y = 2 
Vậy x = 1 và y = 1  HẾT 
Document Outline

• bia .pdf
  • BỘ ĐỀ GIỮA KÌ 1
  • MÔN TOÁN LỚP 8 HÀ NỘI 2021