Đề thi giữa học kì 2 môn Toán 6 năm 2023 - 2024 sách Chân trời sáng tạo | Đề 3
Bộ đề thi giữa học kì 2 môn Toán 6 năm 2023 - 2024 sách Chân trời sáng tạo gồm 5 đề thi, có đáp án, hướng dẫn chấm và bảng ma trận kèm theo, giúp thầy cô xây dựng đề thi giữa kì 2 cho học sinh của mình theo chương trình mới.
Chủ đề: Đề giữa HK2 Toán 6
Môn: Toán 6
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TOÁN – LỚP 6
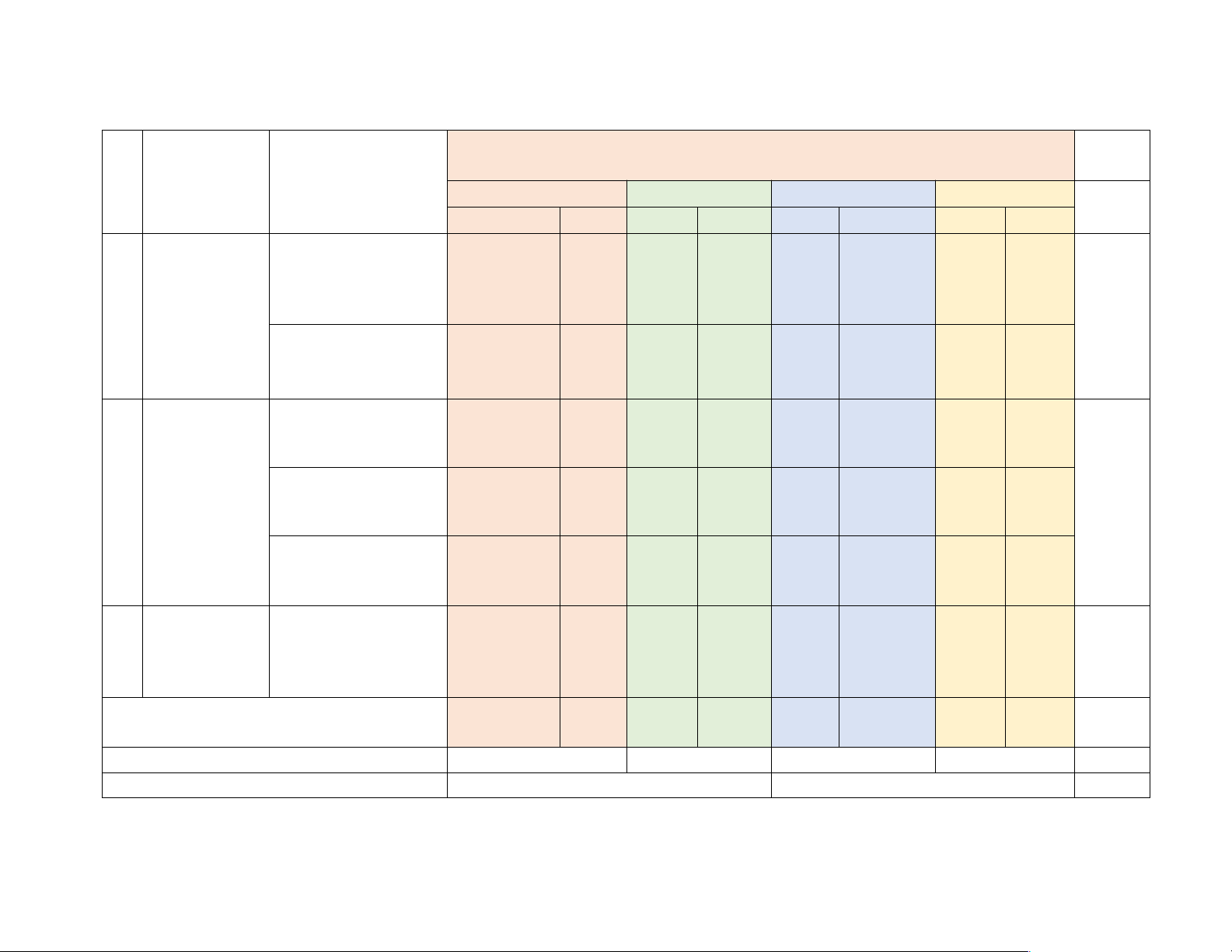
Mức độ đánh giá T ổng Nội dung/Đơn vị % điểm TT Chủ đề kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TNKQ TL TNKQ TL TNKQ TL TNKQ TL Phân số. Tính chất cơ 5 1 bản của phân số. So (TN1,2,3,4,5 (TN12) sánh phân số ) 0,25đ
1 Phân số (17 tiết) 1,25đ 5,5 Các phép tính với phân 3 1 số (TL 4;5;6) (TL7) 3,5 đ 0,5đ
Hình có trục đối xứng. 1 1 (TN6) (TL1) Tính đối xứng 0,25đ 0,5đ
của hình phẳng Hình có tâm đối xứng 1 1
2 trong thế giới tự (TN7) (TL2) 2,5 nhiên 0,25đ 1,0 đ (9 tiết) Vai trò của đối xứng 2 trong thế giới tự nhiên (TN 8;9) 0,5đ
Điểm, đường thẳng, tia 2 1 Các hình hình (TN 10;11 ) (TL3) 3 học cơ bản 0,5đ 1,5 đ (8 tiết) 2,0 Tổng: Số câu 10 3 2 3 1 19 Điểm 2,75 3,0 0,25 3,5 0,5 10,0 Tỉ lệ % 57,5% 2,5% 35% 5% 100% Tỉ lệ chung 60% 40% 100%
Chú ý: Tổng tiết : 34 tiết 1
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TOÁN – LỚP 6 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
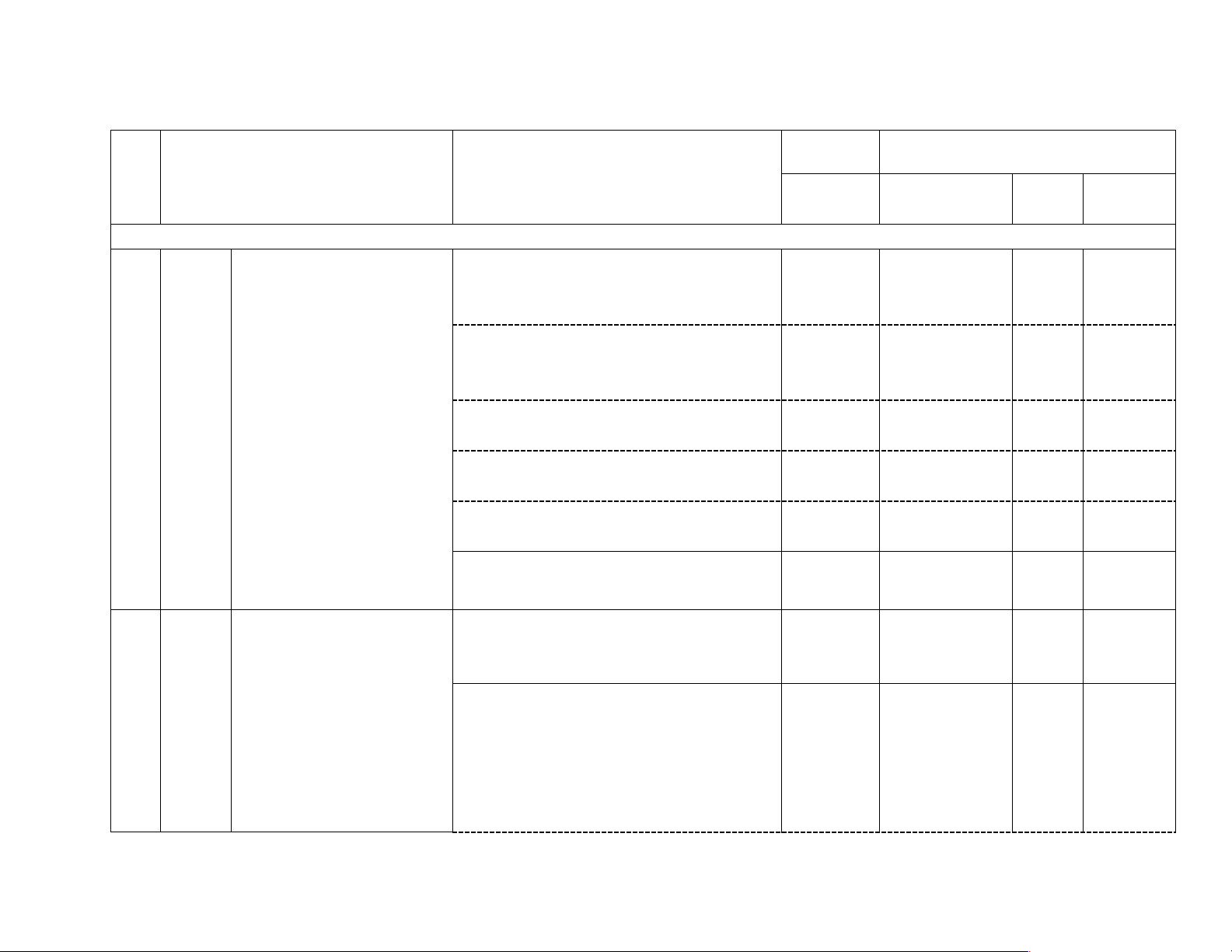
Nhận biết Thông hiểu Vận Vận dụng dụng cao SỐ - ĐAI SỐ 1 Phân Nhận biết: 1TN số
– Nhận biết được phân số với tử số hoặc (TN1)
mẫu số là số nguyên âm.
-Nhận biết được khái niệm hai phân số 1TN
bằng nhau và nhận biết được quy tắc bằng (TN2)
Phân số. Tính chất cơ bản nhau của hai phân số.
của phân số. So sánh phân -Nêu được hai tính chất cơ bản của phân 1TN số số. (TN3)
- Nhận biết được số đối của một phân số. 1TN (TN4)
- Nhận biết được hỗn số dương. 1TN (TN5) Thông hiểu: 1TN
– So sánh được hai phân số cho trước. (TN11)
Các phép tính với phân số Vận dụng: 2 TL
- Thực hiện được các phép tính cộng, trừ, (TL4,5) nhân, chia với phân số. Vận dụng:
- Vận dụng được các tính chất giao hoán,
kết hợp, phân phối của phép nhân đối với
phép cộng, quy tắc dấu ngoặc với phân số
trong tính toán (tính viết và tính nhẩm,
tính nhanh một cách hợp lí). 2
- Tính được giá trị phân số của một số cho 1TL
trước và tính được một số biết giá trị phân (TL6) số của số đó.
- Giải quyết được một số vấn đề thực tiễn
(đơn giản, quen thuộc) gắn với các phép
tính về phân số (ví dụ: các bài toán liên
quan đến chuyển động trong Vật lí,...).
Vận dụng cao: 1TL
– Vận dụng được kiến thức số học vào (TL7)
giải quyết những vấn đề thực tiễn (phức
hợp, không quen thuộc).
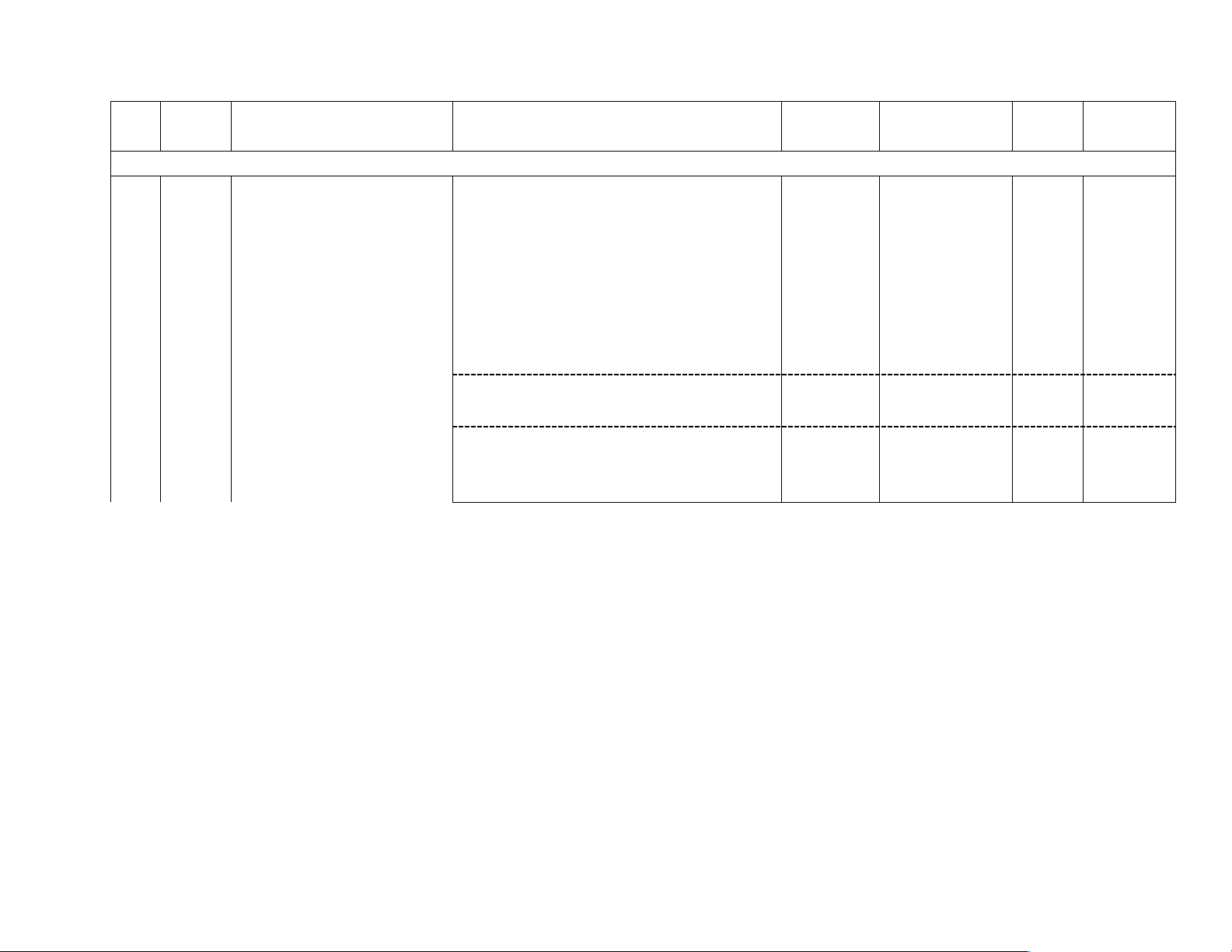
HÌNH HỌC VÀ ĐO LƯỜNG 2 Tính
Hình có trục đối xứng. Nhận biết: đối
-Nhận biết được trục đối xứng của một 1TN xứng hình phẳng. (TN6) của
Nhận biết được những hình phẳng trong 1TL hình
tự nhiên có trục đối xứng (khi quan sát (TL1) phẳng trên hình ảnh 2 chiều). trong Nhận biết: 1TN thế
Nhận biết được tâm đối xứng của một (TN7)
giới tự Hình có tâm đối xứng hình phẳng. 1TL nhiên (TL2)
Vai trò của đối xứng trong Nhận biết: 2TN thế giới tự nhiên
-Nhận biết được tính đối xứng trong Toán (TN 8;9)
học, tự nhiên, nghệ thuật, kiến trúc, công nghệ chế tạo,...
-Nhận biết được vẻ đẹp của thế giới tự
nhiên biểu hiện qua tính đối xứng (ví dụ:
nhận biết vẻ đẹp của một số loài thực vật, 3
động vật trong tự nhiên có tâm đối xứng
hoặc có trục đối xứng).
MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SU ẤT 3 Các
Điểm, đường thẳng, tia Nhận biết: hình
-Nhận biết được những quan hệ cơ bản hình
giữa điểm, đường thẳng: điểm thuộc 1TL học cơ
đường thẳng, điểm không thuộc đường (TL3) bản
thẳng; tiên đề về đường thẳng đi qua hai điểm phân biệt.
-Nhận biết được khái niệm hai đường
thẳng cắt nhau, song song.
-Nhận biết được khái niệm ba điểm thẳng 1TN
hàng, ba điểm không thẳng hàng. (TN11)
- Hiểu được khái niệm điểm nằm giữa hai 1TN điểm. (TN10)
Hiểu được khái niệm tia. 4
C. ĐỀ KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2023-2024
Môn: TOÁN – Lớp 6
Thời gian: 90 phút (không kể thời gian giao đề)
(Đề gồm có 03 trang)
Phần 1. Trắc nghiệm khách quan. (3,0 điểm)
Hãy khoanh tròn vào phương án đúng trong mỗi câu dưới đây:
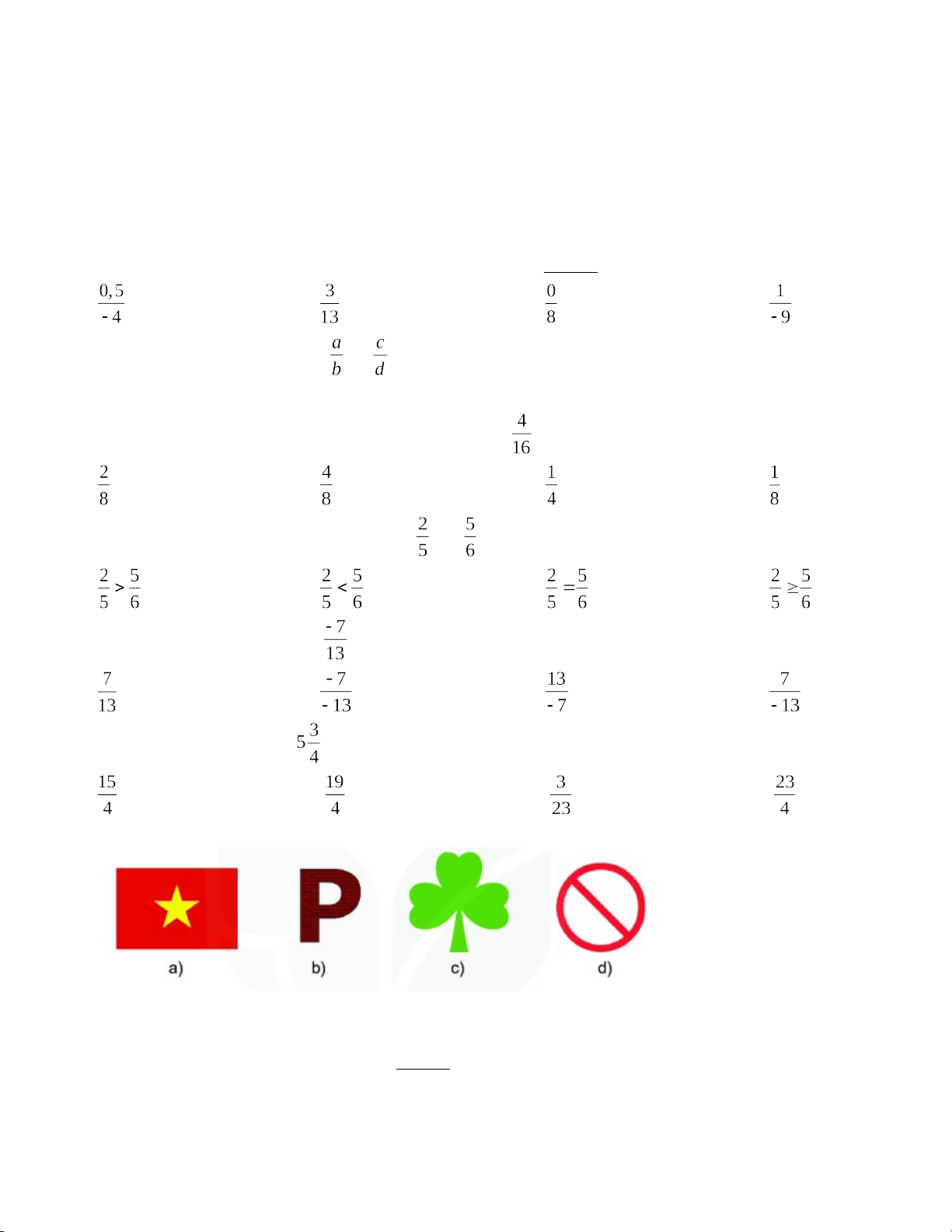
Câu 1. [NB_TN1] Trong các cách viết sau, cách viết nào không cho ta phân số: A. B. C. D.
Câu 2. [NB_TN2] Hai phân số và bằng nhau khi nào? A. ab = cd B. ac = bd C. ad = bc D. cd = ab
Câu 3. [NB_TN3] Sau khi rút gọn tối giản phân số ta được phân số A. B. C. D.
Câu 4. [TH_TN12] So sánh hai phân số: và A. B. C. D.
Câu 5. [NB_TN4] Số đối của là: A. B. C. D.
Câu 6. [NB_TN5] Hỗn số
được viết dạng phân số là: A. B. C. D.
Câu 7. [NB_TN8] Hình nào dưới đây có trục đối xứng?
A. Hình a), Hình b), Hình c)
B. Hình a), Hình c), Hình d)
C. Hình b), Hình c), Hình d)
D. Hình a) và Hình c)
Câu 8. [NB_TN7] Hình nào dưới đây không có tâm đối xứng
A. Lục giác đều B. Tam giác đều C. Hình bình hành D. Hình thoi
Câu 9. [NB_TN6] Phát biểu nào dưới đây là đúng?
A. Hình thoi có tâm đối xứng nhưng không có trục đối xứng. 5
B. Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng.
C. Hình bình hành vừa có tâm đối xứng, vừa có trục đối xứng.
D. Hình chữ nhật có trục đối xứng nhưng không có tâm đối xứng.
Câu 10. [NB_TN9] Trong các chữ cái sau, chữ cái nào nào có tâm đối xứng ?
A. Chữ H, I, N B. Chữ T, E, C C. Chữ E, H, I D. Chữ C, H, I
Câu 11. [NB_TN10] Kể tên các tia trong hình vẽ sau: A. Ox B. Ox, Oy, Oz, Ot C. Oz, Ox, Oy D. xO, yO, zO, tO
Câu 12. [NB_TN11] Chọn câu đúng
A. Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng
B. Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
C. Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
D. Tất cả đáp án trên đều sai
Phần 2: Tự luận (7,0 điểm)
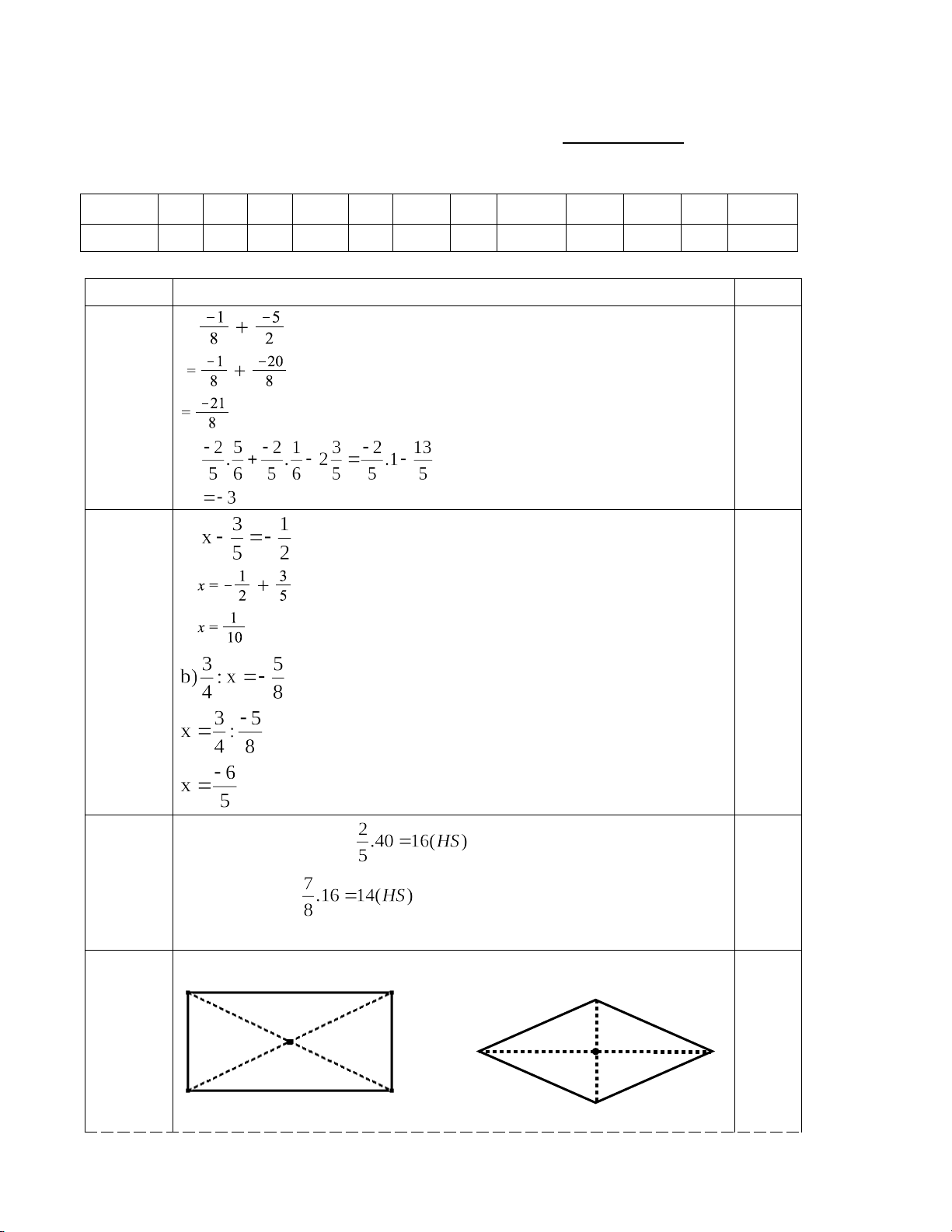
Câu 13. (1,0 điểm). Thực hiện phép tính : a) [VD_TL4] b) [VD_TL4]
Câu 14. (1,0 điểm )Tìm x biết: a) [VD_TL5] b) [VD_TL5]
Câu 15. [VD_TL6] (1,5 điểm).Lớp 6A có 40 học sinh. Kết quả xếp loại học lực cuối năm gồm ba loại
giỏi, khá và trung bình. Số học sinh trung bình chiếm số học sinh cả lớp. Số học sinh khá bằng số
học sinh trung bình.Tính số học sinh mỗi loại của lớp 6A
Câu 16. (1,5 điểm )
a) [NB_TL1] Tìm tâm đối xứng của các hình sau:
b) [NB_TL2] Tìm trục đối xứng của hình sau: 6
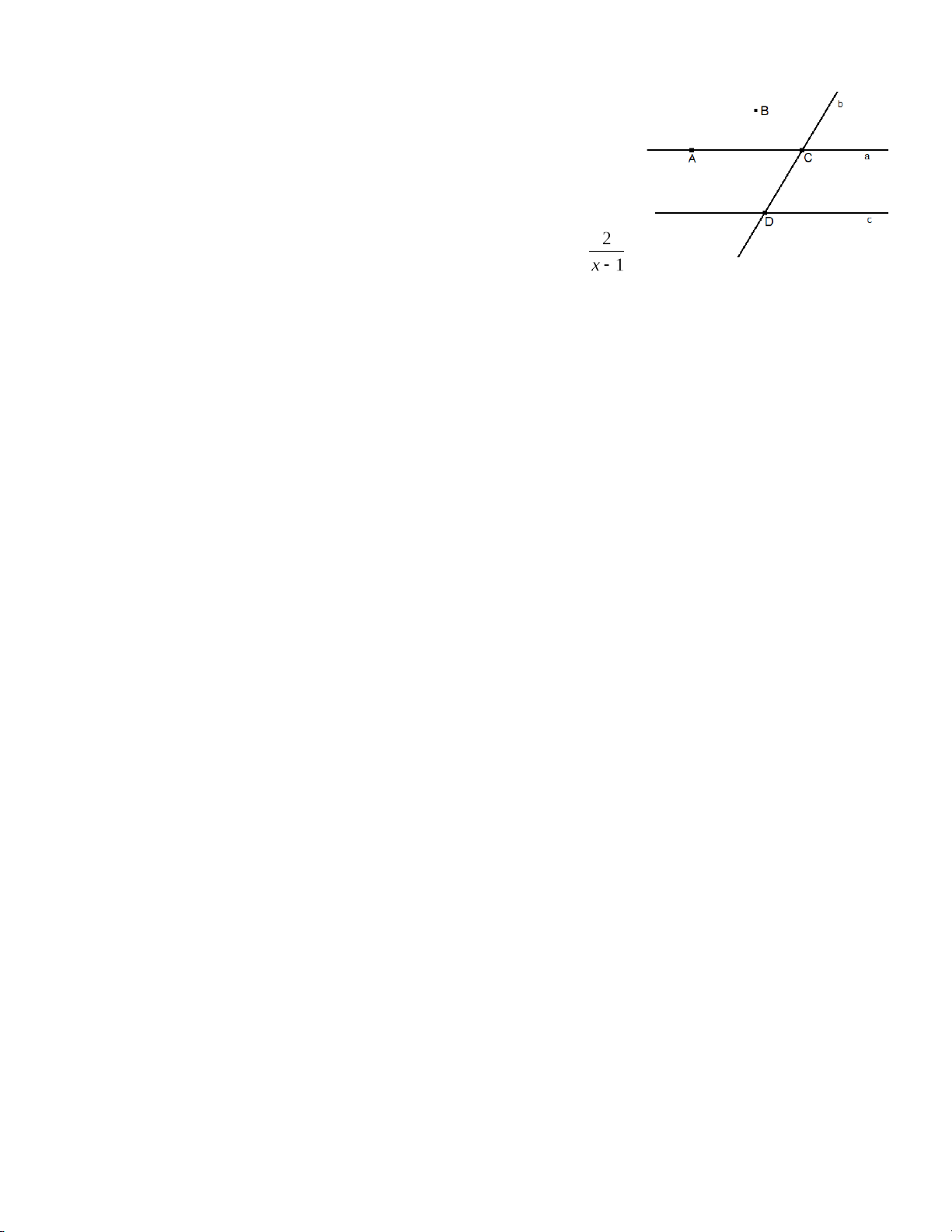
Câu 17. [NB_TL3] (1,5 điểm) Cho hình vẽ bên
a) Điểm nào thuộc đường thẳng a? Điểm nào không thuộc đường thẳng a?
b) Tìm giao điểm của hai đường thẳng a và b?
c) Kể tên hai đường thẳng song song? Hai đường thẳng cắt nhau?
Câu 18. [VDC_TL7] (0,5 điểm)
Tìm tất các số nguyên x sao cho phân số sau có giá trị nguyên : -------Hết------- 7
D. ĐÁP ÁN VÀ THANG ĐIỂM
ĐÁP ÁN & HƯỚNG DẪN CHẤM
Môn : Toán – Lớp: 6
I.TRẮC NGHIỆM: (3,0 điểm) Mỗi phương án chọn đúng ghi 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đ/án A C C B A D B B B A B C
II. TỰ LUẬN: (7,0 điểm) Bài Lời giải Điểm 13 a) (1,0đ) 0,25 0,25 0,25 b) 0,25 14 a) (1,0đ) 0,25 0,25 0,25 0,25 15 0,5 Số HS trung bình là : (1,5đ) 0,5 Số HS khá là :
Số HS giỏi là : 100 – (16 + 14) = 10(HS) 0,5 16a
a) Tìm tâm đối xứng của các hình sau: 1,0 (1,0đ) 8 16b
b) Tìm trục đối xứng của hình sau: 0,5 (0,5đ) 17
a) Điểm thuộc đường thẳng a là: điểm A, điểm C 0,25
(1,5đ) Điểm không thuộc đường thẳng a là: điểm B, điểm D 0,25
b) Giao điểm của hai đường thẳng a và b là: điểm C 0,25
c) Hai đường thẳng song song là: đường thẳng a và c 0,25
Hai đường thẳng cắt nhau là: đường thẳng a và b; đường thẳng c 0,5 và b. 18 2
(0,5đ) Để phân số
có giá trị nguyên thì : x 1 0,25
Vì x nguyên x 1;0; 2; 3 0,25
Học sinh làm cách khác nếu đúng vẫn đạt điểm tối đa ---Hết--- 9
Document Outline
- A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TOÁN – LỚP 6
- B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TOÁN – LỚP 6
- (Đề gồm có 03 trang)
- C. Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng