Đề thi giữa học kỳ 2 Toán 10 năm 2023 – 2024 trường THPT Hồ Nghinh – Quảng Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra định kỳ giữa học kỳ 2 môn Toán 10 năm học 2023 – 2024 trường THPT Hồ Nghinh, tỉnh Quảng Nam; đề thi có đáp án và hướng dẫn chấm điểm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Thông tin:

17 trang 5 tháng trước

Tác giả:

Profile M. Hậu
1/ 5 – Mã đề 101
SỞ GD&ĐT QUẢNG NAM
TRƯỜNG THPT HỒ NGHINH
(Đề thi có 05 trang)
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2023 - 2024
MÔN TOÁN – Khối lớp 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh:…………………………. Số báo danh:…………….
I. PHẦN TRẮC NGHIỆM (7.0 ĐIỂM)
Câu 1: Trong mặt phẳng
Oxy
, cho phương trình chính tắc của parabol là
2
2y px=
, với
0p >
. Khi đó,
parabol có tiêu điểm là:
A.
;0
2
p
F

−


. B.
0;
2
p
F



. C.
0;
2
p
F

−


. D.
;0
2
p
F



.
Câu 2: Trong mặt phẳng
, phương trình chính tắc của hypebol có dạng là:
A.
22
22
1
xy
ab
+=
. B.
2
y px=
. C.
22
22
1
xy
ab
−=
. D.
2
2y px=
.
Câu 3: Giá trị
2=x
là nghiệm của phương trình nào sau đây?
A.
2
44−−= −
xx x
. B.
2 23 2
+= −xx
. C.
21+= −xx
. D.
13−= −xx
.
Câu 4: Điểm nào dưới đây không thuộc đồ thị của hàm số
2
2yx= −
?
A.
( )
1; 2−
. B.
( )
0; 0
. C.
( )
1; 2−
. D.
( )
2; 8−
.
Câu 5: Đồ thị hàm số bậc hai
2
= ++
y ax bx c
( )
0≠a
là một đường parabol có đỉnh là điểm
A.
;
24
∆

−−


b
I
aa
. B.
;
4
∆



b
I
aa
. C.
;
4
∆

−−


b
I
aa
. D.
;
22
∆

−−


b
I
aa
.
Câu 6: Trong mặt phẳng
Oxy
, đường thẳng
d
:
14
23
xt
yt
= −
=−+
có một vectơ chỉ phương là:
A.
( )
4;3u = −
. B.
( )
4;3
u =
. C.
( )
3; 4u =
. D.
( )
1; 2u = −
.
Câu 7: Tam thức bậc hai nào sau đây có hệ số
3; 2; 7ab c= =−=−
?
A.
2
3 27xx− ++
. B.
2
3 27xx+−
. C.
2
3 27
xx−−
. D.
2
3 27
xx−+
.
Câu 8: Trong mặt phẳng
Oxy
, đường thẳng
: 3 20xy∆+−=
song song với đường thẳng có phương
trình nào sau đây?
A.
30xy−=
. B.
3 20xy+−=
. C.
2 6 10xy+ +=
. D.
2 6 40xy− − +=
.
Câu 9: Cho parabol có đồ thị như hình vẽ sau:
Mã đề 101
2/ 5 – Mã đề 101
Trục đối xứng của parabol là:
A.
1.x =
B.
3.x
=
C.
2.x =
D.
2.y =
Câu 10: Tập nghiệm của phương trình:
2
31x −=−
là:
A.
{
}
0
. B.
{ }
2
. C.
{ }
2; 2−
. D.
∅
.
Câu 11: Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
00
;Mx y
đến đường thẳng
:0Ax By C∆ + +=
được tính bởi công thức:
A.
( )
00
22
,
.
xyC
dM
AB
++
∆=
+
. B.
( )
00
22
,
.
Ax By C
dM
AB
++
∆=
+
.
C.
(
)
00
22
,
Ax By C
dM
AB
++
∆=
+
. D.
( )
00
22
,
.
Ax By C
dM
AB
+−
∆=
+
.
Câu 12: Trong mặt phẳng
, đường elip
22
1
16 9
+=
xy
có một giao điểm với trục tung là:
A.
0; 3
. B.
3; 0
. C.
( )
0; 4
. D.
( )
4; 0
.
Câu 13: Trong mặt phẳng
Oxy
, cho phương trình
( )
22
2 2 0, , ,x y ax by c a b c+ + + += ∈
là phương
trình đường tròn. Khi đó
,,abc
thỏa mãn điều kiện nào sau đây?
A.
22
0abc+ −>
. B.
22
0abc+ −<
. C.
22
0abc− +<
. D.
22
0abc− +>
. .
Câu 14: Cho hàm số
2
y ax bx c
= ++
( 0)a
≠
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
0.
c =
B.
0.a >
C.
0.c <
D.
0.a <
Câu 15: Cho hàm số bậc hai
2
y ax bx c
= ++
có đồ thị như hình bên dưới.
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A.
( 4; )− +∞
. B.
(0; )+∞
. C.
(1; )+∞
. D.
( ;1)−∞
.
Câu 16: Hàm số nào dưới đây là hàm số bậc hai
3/ 5 – Mã đề 101
A.
3
1
21
2
yxx= −+
. B.
2
1
21
y
xx
=
++
. C.
31
yx
=−+
. D.
2
1
1
2
y xx
=− +−
.
Câu 17: Trong mặt phẳng
Oxy
, đường thẳng
(
)
( )
22
: 0, 0d ax by c a b
+ += + ≠
. Vectơ nào sau đây là
một vectơ pháp tuyến của đường thẳng
( )
d
?
A.
( )
;n ba= −
. B.
( )
;n ab=
. C.
( )
;n ba=
. D.
( )
;n ab= −
.
Câu 18: Bảng dưới đây cho biết nồng độ bụi
2.5PM
trong không khí theo thời gian trong ngày
25 3 2021−−
tại một trạm quan trắc ở Thủ đô Hà Nội:
Nồng độ bụi
2.5
PM
tại thời điểm 8 giờ là:
A.
64,58.
B.
74,27.
C.
57,9.
D.
81,78.
Câu 19: Tìm tập xác định
D
của hàm số
( )
23
1
x
fx
x
+
=
+
.
A.
D =
. B.
( )
0;D = +∞
. C.
( )
;0
D = −∞
. D.
{ }
\ 1.D = −
Câu 20: Trong mặt phẳng
Oxy
, đường tròn
22
10xy+ −=
tiếp xúc với đường thẳng nào trong các đường
thẳng dưới đây?
A.
0xy+=
. B.
3 4 50xy− +=
. C.
3 4 10xy+ −=
. D.
10xy
+ −=
.
Câu 21: Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng
: 3 20xy∆ − +=
và
: 3 10xy
′
∆ + −=
A.
90
. B.
60
. C.
30
. D.
120
.
Câu 22: Trong mặt phẳng
, đường thẳng
d
có một vectơ chỉ phương là
( )
3; 4u = −
. Đường thẳng
∆
vuông góc với
d
có một vectơ pháp tuyến là:
A.
( )
2
4;3 .n −=

B.
( )
4
3; 4 .n −=

C.
( )
1
.4;3n =

D.
( )
3
.3; 4n =

Câu 23: Tập nghiệm của bất phương trình
2
3 20xx− + −≥
là:
A.
[ ]
1; 2−
. B.
[ ]
2;1−
. C.
( )
1; 2
. D.
[ ]
1; 2
.
Câu 24: Cho tam thức
( ) ( )
2
0,f x ax bx c a= ++ ≠
2
4b ac∆= −
. Để
( )
0
fx≤
với
x∀∈
thì
A.
0
.
0
a <
∆≥
B.
0
.
0
a >
∆≤
C.
0
.
0
a <
∆≤
D.
0
.
0
a ≤
∆<
Câu 25: Cho parabol
2
y x bx c=++
có tọa độ đỉnh
(1; 2)I
. Mệnh đề nào sau đây đúng?
A.
2
0x bx c+ +>
với
x∀∈
. B.
2
0x bx c+ +<
với
x∀∈
.
C.
2
0x bx c+ +≤
với
x∀∈
. D.
2
3x bx c+ +≥
với
x∀∈
.
Câu 26: Trong mặt phẳng
, đường tròn tâm
(3; 7)I −
, bán kính
3R =
có phương trình là:
A.
( ) ( )
22
3 79+ +− =xy
. B.
(
) ( )
22
3 79+ ++ =xy
.
4/ 5 – Mã đề 101
C.
( ) ( )
22
3 79− ++ =xy
. D.
( ) ( )
22
3 73− ++ =xy
.
Câu 27: Trong mặt phẳng
Oxy
, tọa độ giao điểm của hai đường thẳng
3 4 70xy+ −=
và
4 3 26 0xy−−=
là:
A.
( )
5; 2−−
. B.
( )
5; 2
. C.
( )
5; 2−
. D.
( )
5; 2−
. .
Câu 28: Trong các tam thức sau, tam thức nào luôn âm với mọi
x ∈
?
A.
( )
2
34fx x x=−− −
. B.
( )
2
34fx x x=−− +
.
C.
( )
2
44fx x x=−− −
. D.
( )
2
34fx x x=−+
.
Câu 29: Bình phương hai vế của phương trình
22
3 21xx x x−= + −
và rút gọn ta được phương trình
nào dưới đây?
A.
2
2 3 1 0.xx+ −=
B.
1 0.x −=
C.
1 0.x−−=
D.
2
3 1 0.x −=
Câu 30: Số nghiệm nguyên dương của phương trình
13xx−=−
là:
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 31: Trong mặt phẳng
,Oxy
đường thẳng đi qua
( )
1; 2A −
, nhận
( )
2; 4n = −
làm véctơ pháp tuyến có
phương trình là:
A.
2 40xy− −=
. B.
40xy++=
. C.
2 40xy−+ − =
. D.
2 50xy− +=
.
Câu 32: Hàm số
( )
y fx=
được cho bằng bảng sau:
Tập giá trị của hàm số là:
A.
{ }
1; 2; 3; 4; 5;6; 7T =
. B.
{ }
3; 4; 5; 6; 7; 8; 9T =
.
C.
T =
. D.
{ }
3; 4; 5;6; 7;8;9;10T =
.
Câu 33: Trong mặt phẳng
Oxy
, cho đường tròn
( ) ( ) ( )
22
: 1 3 25Cx y++− =
. Trong các mệnh đề sau
đây, phát biểu nào sai?
A.
( )
C
có tâm
( )
1; 3A
. B.
( )
C
có bán kính
5R =
.
C.
( )
C
có tâm
( )
1; 3I −
. D.
( )
C
đi qua điểm B(4;3).
Câu 34: Parabol dưới đây là đồ thị của hàm số nào?
A.
2
22yx x=+−
. B.
2
21yx x=−−
. C.
2
21yx x=+−
. D.
2
21yx x=−− +
.
5/ 5 – Mã đề 101
Câu 35: Bảng xét dấu nào dưới đây là bảng xét dấu của tam thức bậc hai
2
() 6fx x x= −−
?
A. . B. .
C. . D. .
II. PHẦN TỰ LUẬN (3.0 ĐIỂM )
Câu 1 (1 điểm).
Giải phương trình:
2
2 31xx x++=−
Câu 2. (1 điểm)
Cho hàm số
2
28yx x=+−
có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho.
Câu 3: (1 điểm)
Trong mặt phẳng hệ toạ độ
Oxy
, cho đường thẳng
: 0.xy∆ +=
Đường tròn
( )
C
cắt
∆
tại hai
điểm
,AB
sao cho
26AB =
. Các tiếp tuyến của
( )
C
tại hai điểm
,AB
cắt nhau tại điểm
( )
0; 6 .M −
a. Viết phương trình đường thẳng d qua M và vuông góc với
∆
.
b. Viết phương trình đường tròn
( )
C
.
---------------------------HẾT ---------------------
1 / 5 – Mã đề 102
SỞ GD&ĐT QUẢNG NAM
TRƯỜNG THPT HỒ NGHINH
(Đề thi có 05 trang)
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2023 - 2024
MÔN TOÁN – Khối lớp 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh:………………………….. Số báo danh:…………………...
I. PHẦN TRẮC NGHIỆM (7.0 ĐIỂM)
Câu 1: Trong mặt phẳng
, phương trình chính tắc của hypebol có dạng là:
A.
22
22
1
xy
ab
−=
. B.
22
22
1
xy
ab
+=
. C.
2
y px=
. D.
2
2y px=
.
Câu 2: Điểm nào dưới đây không thuộc đồ thị của hàm số
2
2yx= −
?
A.
( )
0; 0
. B.
( )
2; 8−
. C.
(
)
1; 2−
. D.
( )
1; 2
−
.
Câu 3: Hàm số nào dưới đây là hàm số bậc hai
A.
3
1
21
2
yxx= −+
. B.
2
1
1
2
y xx=− +−
. C.
31yx=−+
. D.
2
1
21
y
xx
=
++
.
Câu 4: Cho parabol có đồ thị như hình vẽ sau:
Trục đối xứng của parabol là:
A.
2.y =
B.
3.x =
C.
1.x =
D.
2.x =
Câu 5: Trong mặt phẳng
Oxy
, đường thẳng
: 3 20xy∆+−=
song song với đường thẳng có phương
trình nào sau đây?
A.
30
xy−=
. B.
2 6 40xy− − +=
. C.
3 20xy+−=
. D.
2 6 10xy+ +=
.
Câu 6: Giá trị
2=x
là nghiệm của phương trình nào sau đây?
A.
13−= −xx
. B.
2 23 2+= −xx
.
C.
21+= −xx
. D.
2
44−−= −xx x
.
Câu 7: Cho hàm số
2
y ax bx c= ++
( 0)a ≠
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
Mã đề 102
2 / 5 – Mã đề 102
A.
0.a >
B.
0.a <
C.
0.c =
D.
0.c <
Câu 8: Tam thức bậc hai nào sau đây có hệ số
3; 2; 7ab c= =−=−
?
A.
2
3 27xx
−−
. B.
2
3 27xx
+−
. C.
2
3 27xx
− ++
. D.
2
3 27xx−+
.
Câu 9: Trong mặt phẳng
Oxy
, đường thẳng
( )
(
)
22
: 0, 0
d ax by c a b
+ += + ≠
. Vectơ nào sau đây là
một vectơ pháp tuyến của đường thẳng
( )
d
?
A.
( )
;n ba=
. B.
( )
;n ab=
. C.
( )
;n ab= −
. D.
( )
;n ba= −
.
Câu 10: Trong mặt phẳng
, đường elip
22
1
16 9
+=
xy
có một giao điểm với trục tung là:
A.
( )
0; 4
. B.
( )
4; 0
. C.
3; 0
. D.
0; 3
.
Câu 11: Trong mặt phẳng
Oxy
, đường thẳng
d
:
14
23
xt
yt
= −
=−+
có một vectơ chỉ phương là:
A.
(
)
3; 4
u =
. B.
( )
1; 2u = −
. C.
( )
4;3u = −
. D.
( )
4;3
u =
.
Câu 12: Bảng dưới đây cho biết nồng độ bụi
2.5PM
trong không khí theo thời gian trong ngày
25 3 2021
−−
tại một trạm quan trắc ở Thủ đô Hà Nội:
Nồng độ bụi
2.5PM
tại thời điểm 8 giờ là:
A.
57,9.
B.
81,78.
C.
74,27.
D.
64,58.
Câu 13: Trong mặt phẳng
Oxy
, cho phương trình
( )
22
2 2 0, , ,x y ax by c a b c+ + + += ∈
là phương
trình đường tròn. Khi đó
,,abc
thỏa mãn điều kiện nào sau đây?
A.
22
0abc+ −<
. B.
22
0abc− +<
. C.
22
0abc− +>
. . D.
22
0abc+ −>
.
Câu 14: Cho hàm số bậc hai
2
y ax bx c= ++
có đồ thị như hình bên dưới.
3 / 5 – Mã đề 102
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A.
(0; )
+∞
. B.
(1; )+∞
. C.
( ;1)−∞
. D.
( 4; )
− +∞
.
Câu 15: Trong mặt phẳng
Oxy
, cho phương trình chính tắc của parabol là
2
2y px=
, với
0p >
. Khi đó,
parabol có tiêu điểm là:
A.
0;
2
p
F

−


. B.
;0
2
p
F



. C.
0;
2
p
F



. D.
;0
2
p
F

−


.
Câu 16: Tập nghiệm của phương trình:
2
31x −=−
là:
A.
{ }
0
. B.
{
}
2
. C.
∅
. D.
{ }
2; 2−
.
Câu 17: Đồ thị hàm số bậc hai
2
= ++y ax bx c
( )
0≠a
là một đường parabol có đỉnh là điểm
A.
;
4
∆

−−


b
I
aa
. B.
;
24
∆

−−


b
I
aa
. C.
;
22
∆

−−


b
I
aa
. D.
;
4
∆



b
I
aa
.
Câu 18: Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
00
;Mx y
đến đường thẳng
:0Ax By C∆ + +=
được tính bởi công thức:
A.
(
)
00
22
,
Ax By C
dM
AB
++
∆=
+
. B.
( )
00
22
,
.
xyC
dM
AB
++
∆=
+
.
C.
( )
00
22
,
.
Ax By C
dM
AB
++
∆=
+
. D.
( )
00
22
,
.
Ax By C
dM
AB
+−
∆=
+
.
Câu 19: Trong mặt phẳng
Oxy
, đường tròn
22
10xy+ −=
tiếp xúc với đường thẳng nào trong các đường
thẳng dưới đây?
A.
10
xy+ −=
. B.
3 4 10xy+ −=
. C.
3 4 50xy− +=
. D.
0xy+=
.
Câu 20: Trong mặt phẳng
, đường thẳng
d
có một vectơ chỉ phương là
( )
3; 4u = −
. Đường thẳng
∆
vuông góc với
d
có một vectơ pháp tuyến là:
A.
( )
1
.4; 3n =

B.
( )
4
3; 4 .n −=

C.
( )
2
4;3 .n −=

D.
( )
3
.3; 4n =

Câu 21: Tìm tập xác định
D
của hàm số
( )
23
1
x
fx
x
+
=
+
.
A.
( )
0;D = +∞
. B.
D
=
. C.
{
}
\ 1.D = −
D.
( )
;0D = −∞
.
Câu 22: Số nghiệm nguyên dương của phương trình
13xx−=−
là:
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 23: Trong mặt phẳng
, đường tròn tâm
(3; 7)I −
, bán kính
3R =
có phương trình là:
4 / 5 – Mã đề 102
A.
( ) ( )
22
3 79+ ++ =xy
. B.
( ) ( )
22
3 73− ++ =xy
.
C.
( ) ( )
22
3 79− ++ =xy
. D.
( ) ( )
22
3 79+ +− =xy
.
Câu 24: Bảng xét dấu nào dưới đây là bảng xét dấu của tam thức bậc hai
2
() 6fx x x= −−
?
A. . B. .
C. . D. .
Câu 25: Cho tam thức
( ) ( )
2
0,f x ax bx c a= ++ ≠
2
4b ac∆= −
. Để
( )
0fx≤
với
x∀∈
thì
A.
0
.
0
a <
∆≥
B.
0
.
0
a ≤
∆<
C.
0
.
0
a >
∆≤
D.
0
.
0
a <
∆≤
Câu 26: Bình phương hai vế của phương trình
22
3 21xx x x−= + −
và rút gọn ta được phương trình
nào dưới đây?
A.
2
2 3 1 0.xx+ −=
B.
1 0.x −=
C.
2
3 1 0.x −=
D.
1 0.x−−=
Câu 27: Trong mặt phẳng
Oxy
, cho đường tròn
( ) ( ) ( )
22
: 1 3 25Cx y++− =
. Trong các mệnh đề sau
đây, phát biểu nào sai?
A.
( )
C
có tâm
( )
1; 3A
. B.
( )
C
có tâm
( )
1; 3I −
.
C.
( )
C
có bán kính
5R =
. D.
( )
C
đi qua điểm B(4;3).
Câu 28: Trong mặt phẳng
,Oxy
đường thẳng đi qua
( )
1; 2A −
, nhận
( )
2; 4n = −
làm véctơ pháp tuyến có
phương trình là:
A.
40xy++=
. B.
2 40xy−+ − =
. C.
2 40xy− −=
. D.
2 50xy− +=
.
Câu 29: Trong mặt phẳng
Oxy
, tọa độ giao điểm của hai đường thẳng
3 4 70xy+ −=
và
4 3 26 0xy−−=
là:
A.
( )
5; 2−−
. B.
( )
5; 2−
. C.
( )
5; 2
. D.
( )
5; 2−
. .
Câu 30: Parabol dưới đây là đồ thị của hàm số nào?
A.
2
22yx x=+−
. B.
2
21yx x=−−
. C.
2
21yx x=+−
. D.
2
21yx x=−− +
.
Câu 31: Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng
: 3 20xy∆ − +=
và
: 3 10xy
′
∆ + −=
A.
30
. B.
60
. C.
120
. D.
90
.
5 / 5 – Mã đề 102
Câu 32: Cho parabol
2
y x bx c=++
có tọa độ đỉnh
(1; 2)I
. Mệnh đề nào sau đây đúng?
A.
2
0x bx c+ +>
với
x∀∈
. B.
2
3x bx c+ +≥
với
x∀∈
.
C.
2
0x bx c+ +<
với
x∀∈
. D.
2
0x bx c+ +≤
với
x∀∈
.
Câu 33: Trong các tam thức sau, tam thức nào luôn âm với mọi
x ∈
?
A.
( )
2
44fx x x=−− −
. B.
( )
2
34fx x x=−− +
.
C.
( )
2
34fx x x=−+
. D.
( )
2
34fx x x=−− −
.
Câu 34: Hàm số
( )
y fx=
được cho bằng bảng sau:
Tập giá trị của hàm số là:
A.
{ }
3; 4; 5;6; 7;8;9;10T =
. B.
{ }
3; 4; 5; 6; 7; 8; 9T =
.
C.
T =
. D.
{ }
1; 2; 3; 4; 5;6; 7T =
.
Câu 35: Tập nghiệm của bất phương trình
2
3 20xx− + −≥
là:
A.
[ ]
2;1−
. B.
[ ]
1; 2−
. C.
( )
1; 2
. D.
[ ]
1; 2
.
II. PHẦN TỰ LUẬN (3.0 ĐIỂM )
Câu 1: (1 điểm)
Giải phương trình:
2
2 59 1xx x− −=−
Câu 2: (1 điểm)
Cho hàm số
2
45yx x=−+ +
có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho.
Câu 3: (1 điểm)
Trong mặt phẳng hệ toạ độ
Oxy
, cho đường thẳng
: 0.∆ −=xy
Đường tròn
( )
C
cắt
∆
tại hai điểm
,AB
sao cho
42=AB
. Các tiếp tuyến của
( )
C
tại hai điểm
,AB
cắt nhau tại điểm
( )
0;8 .M
a. Viết phương trình đường thẳng d qua M và vuông góc với
∆
.
b. Viết phương trình đường tròn
( )
C
.
-------------------HẾT-------------------------
Trang 1/3
SỞ GD&ĐT TỈNH QUẢNG NAM
TRƯỜNG THPT HỒ NGHINH
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA KÌ II. NĂM HỌC: 2023 - 2024
MÔN: TOÁN 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
I/ TRẮC NGHIỆM
Đề\câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
101
D
C
B
C
A
A
C
C
C
D
B
A
A
B
D
D
B
C
D
B
B
B
D
C
A
C
C
A
A
A
D
B
A
C
D
102
A
C
B
D
D
B
A
A
B
D
C
A
D
C
B
C
B
C
C
B
C
A
C
A
D
A
A
D
B
C
B
A
D
B
D
103
C
C
B
B
A
B
C
C
D
D
B
A
A
D
D
A
C
B
D
C
A
B
C
D
B
D
D
B
A
A
B
A
C
C
D
104
B
C
D
A
D
D
C
D
A
C
A
B
A
C
B
D
C
B
C
D
C
C
B
D
A
B
A
D
B
B
D
A
B
A
C
105
D
A
B
B
C
A
A
D
C
C
B
B
D
D
B
A
B
C
A
A
B
A
C
C
D
A
C
B
B
C
D
B
A
D
D
106
A
D
B
D
A
B
A
D
C
A
C
C
D
A
C
D
B
B
C
B
A
D
B
D
A
D
A
B
A
D
C
D
C
B
C
107
A
B
D
D
B
B
C
A
C
A
A
B
D
D
C
B
C
D
B
B
C
C
A
C
D
B
B
A
A
D
D
A
D
A
C
108
C
B
A
D
D
B
D
C
B
A
D
A
C
C
B
B
A
A
C
A
B
A
B
C
D
D
C
A
B
A
D
D
B
C
B
Trang 1/3
II. Phần tự luận. (3,0 điểm)
Gồm các mã đề 102; 104;106;108
Câu
Nội dung yêu cầu
Điểm
Câu 1:
Giải phương trình:
2
2 59 1xx x− −=−
(1,0đ)
Bình phương hai vế của phương trình ta được:
22
2 59 21xx xx
− −= − +
.
0,25
Sau khi thu gọn ta được
2
3 10 0xx
−−=
.
0,25
Từ đó tìm được
2
x = −
hoặc
5
x =
.
0,25
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy chỉ có
5x
=
thỏa mãn.
Vậy nghiệm của phương trình đã cho là
5x =
.
0,25
Câu 2:
Cho hàm số
2
45yx x=−+ +
có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho.
(1,0đ)
Xác định hệ số a, b, c
Xác định được trục đối xứng x = 2
0,25
Toạ độ đỉnh I (2;9)
0,25
Lập bảng giá trị các điểm
0,25
Vẽ đúng Parabol
0,25
Câu 3
Trong mặt phẳng hệ toạ độ
Oxy
, cho đường thẳng
: 0.∆ −=xy
Đường tròn
( )
C
cắt
∆
tại hai điểm
,AB
sao cho
42=AB
. Các tiếp tuyến của
( )
C
tại hai điểm
,AB
cắt nhau tại điểm
( )
0;8 .M
a. Viết phương trình đường thẳng d qua M và vuông góc với
∆
.
b. Viết phương trình đường tròn
( )
C
.
(1,0đ)
a. Đường thẳng d vuông góc với
∆
nên nhận VTPT
(1; 1)n
∆
−
của
∆
làm VTCP.
Suy ra 1 vectơ pháp tuyến của d là
(1; 1)
d
n
.
0,25
Phương trình đường thẳng d:
1( 0) 1( 8) 0 8 0x y xy− + − = ⇔ +−=
.
0,25
b. Giả sử đường tròn
( )
C
có tâm
I
.
Gọi
= ∩H IM AB
. Suy ra
H
là trung điểm của
, 22
2
= =
AB
AB AH
.
(
)
08
, 42
2
MH d M
−
= ∆⇔ =
0,25
Tam giác
AIM
vuông tại
A
,
AH IM⊥
nên có:
2
2
8
.2
42
AH
AH HM IH IH
HM
= ⇔= = =
H là giao điểm của 2 đường thẳng IM và AB (trong đó
,AB IM d≡∆ ≡
). Toạ độ
H
là nghiệm của hpt:
( )
04
4; 4
80 4
−= =

⇔⇒

+−= =

xy x
H
xy y
Ta có
( )
1
5; 3
44
HM
IH IH HM I= ⇒= ⇒
 
22
10R IA AH IH== +=
Vậy phương trình đường tròn
( )
C
là:
( ) (
)
22
5 3 10− +− =xy
.
0.25
Trang 2/3
Gồm các mã đề 101; 103;105;107
Câu
Nội dung yêu cầu
Điểm
Câu 1:
Giải phương trình:
2
2 31
xx x++=−
(1,0đ)
Bình phương hai vế của phương trình ta được
22
2 312x x xx++=− +
.
0,25
Sau khi thu gọn ta được
2
3 20xx+ +=
.
0,25
Từ đó tìm được
1
x = −
hoặc
2
x = −
0,25
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy
1x = −
hoặc
2x = −
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
{ }
1; 2S =−−
.
0,25
Câu 2:
Cho hàm số
2
28yx x
=+−
có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho.
(1,0đ)
Xác định hệ số a, b, c
Xác định được trục đối xứng x = - 1
0,25
Toạ độ đỉnh I (-1;-9)
0,25
Lập bảng giá trị các điểm
0,25
Vẽ đúng Parabol
0,25
Câu 3
Trong mặt phẳng hệ toạ độ
Oxy
, cho đường thẳng
: 0.xy∆ +=
Đường tròn
( )
C
cắt
∆
tại hai điểm
,
AB
sao cho
26AB =
. Các tiếp tuyến của
( )
C
tại hai điểm
,AB
cắt nhau tại điểm
( )
0; 6 .
M −
a. Viết phương trình đường thẳng d qua M và vuông góc với
∆
.
b. Viết phương trình đường tròn
( )
C
.
(1,0đ)
a. Đường thẳng d vuông góc với
∆
nên nhận VTPT
(1; 1)
n
∆
của
∆
làm VTCP.
Suy ra 1 vectơ pháp tuyến của d là
(1; 1)
d
n −
.
0,25
Phương trình đường thẳng d:
1( 0) 1( 6) 0 6 0x y xy
− − + = ⇔ −−=
.
0,25
b. Giả sử đường tròn
( )
C
có tâm
I
.
Gọi
= ∩H IM AB
. Suy ra
H
là trung điểm của
,6
2
AB
AB AH = =
.
( )
06
, 32
2
MH d M
−
= ∆⇔ =
0,25
Tam giác
AIM
vuông tại
A
,
AH IM
⊥
nên có:
2
2
6
.2
32
AH
AH HM IH IH
HM
= ⇔= = =
H là giao điểm của 2 đường thẳng IM và AB (trong đó
,AB IM d≡∆ ≡
).
Toạ độ
H
là nghiệm của hpt:
( )
03
3; 3
60 3
xy x
H
xy y
+= =

⇔ ⇒−

−−= =−

Ta có
(
)
1
4; 2
33
HM
IH IH HM I= ⇒= ⇒ −
 
22
22
R IA AH IH== +=
Vậy phương trình đường tròn
( )
C
là:
( ) ( )
22
4 28xy− ++ =
.
0.25
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa của câu đó.
TRƯỜNG THPT HỒ NGHINH
MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ II
MÔN: TOÁN LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận: 4 câu (30%)
TT
Chương/Chủ
đề
Nội dung/Đơn vị kiến thức
Mức độ đánh giá
Tổng % điểm
Nhận biết Thông hiểu Vận dụng Vận dụng cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1
Hàm số, đồ
thị và ứng
dụng (12 tiết)
Khái niệm cơ bản về hàm số và đồ
thị
3 2 10%
Hàm số bậc hai, đồ thị hàm số bậc
hai và ứng dụng
4 2 1 22%
Dấu của tam thức bậc hai. Bất
phương trình bậc hai một ẩn
1 4 10%
Phương trình quy về phương trình
bậc hai
2 2 1 18%
2
PP tọa độ
trong mặt
phẳng (11
tiết)
Đường thẳng trong mặt phẳng toạ
độ. Phương trình tổng quát và
phương trình tham số của đường
thẳng.
2 2 1
1
13%
Vị trí tương đối giữa 2 đường thẳng,
góc giữa 2 đường thẳng, khoảng
cách từ một điểm đến một đường
thẳng
2 2 8%
Đường tròn trong mặt phẳng toạ độ
và ứng dụng
1 3 13%
Ba đường conic trong mặt phẳng toạ
độ và ứng dụng
3 6%
Tổng
18 17 3 1
Tỉ lệ (%)
36 34 25 5 100%
Tỉ lệ chung (%)
70 30 100%
II. BẢNG ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ II - MÔN TOÁN - LỚP 10
STT
Chương/chủ
đề
Nội dung/Đơn
vị kiến thức
Mức độ kiểm tra, đánh giá
Số câu hỏi theo mức độ nhận thức
NB TH VD VDC
1
HÀM SỐ, ĐỒ
THỊ
VÀ ỨNG
DỤNG
Khái niệm cơ bản về
hàm số và đồ thị
Nhận biết:
- Nhận biết giá trị của hàm số dựa vào bảng giá trị.
- Nhận biết được khoảng đồng biến và nghịch biến
dựa vào đồ thị hàm số
- Nhận điểm có thuộc/ không thuộc đồ thị
Thông hiểu:
- Tìm được tập xác định, tập giá trị của hàm số.
3 (TN)
Câu 1,
Câu 2,
Câu 3
2 (TN)
Câu 4,
Câu 5
Hàm số bậc hai,
đồ thị hàm số bậc
hai và ứng dụng
Nhận biết
- Nhận biết được hàm số bậc hai.
- Nhận biết toạ độ đỉnh, trục đối xứng, bề lõm của
parabol.
Thông hiểu:
- Xác định được các tính chất của đồ thị hàm số bậc
hai.
- Nhận diện được hàm số bậc hai từ đồ thị
Vận dụng:
-Vẽ đồ thị hàm số bậc hai.
4 (TN)
Câu 6,
Câu 7,
Câu 8,
Câu 9
2 (TN)
Câu 10,
Câu 11
TL2
Dấu của tam thức
bậc hai. Bất
phương trình bậc
hai một ẩn
Nhận biết
- Nhận biết hệ số a, b, c của tam thức bậc hai cho
trước.
Thông hiểu
- Xác định dấu của tam thức bậc hai.
+ Tìm được các khoảng hoặc nửa khoảng để tam thức
bậc hai nhận giá trị dương (âm, không dương, không
âm, ...).
+ Tìm tập nghiệm của bpt bậc 2
+ Lập bảng xét dấu tam thức bậc hai cho trước.
1 (TN)
Câu 13,
4 (TN)
Câu 12,
Câu 14
Câu 15,
Câu 16
Phương trình quy
về phương trình
bậc hai
Nhận biết
- Nhận biết nghiệm của phương trình quy về phương
trình bậc hai
Thông hiểu
2 (TN)
Câu 17
2 (TN)
Câu 19
TL1
-Biến đổi phương trình quy về phương trình bậc hai
- Tìm nghiệm phương trình quy về phương trình bậc
hai
Vận dụng:
Giải phương trình dạng:
2
ax bx c dx e+ += +
Câu 18
Câu 20
2
PHƯƠNG
PHÁP TỌA ĐỘ
TRONG MẶT
PHẲNG
Đường thẳng trong
mặt phẳng toạ độ.
Phương trình tổng
quát và phương
trình tham số của
đường thẳng.
Nhận biết
- Nhận biết dạng PTTQ của đường thẳng – Nhận biết
vectơ pháp tuyến, vectơ chỉ phương của đường thẳng
khi biết phương trình.
Thông hiểu
- Xác định được PTTQ của đường thẳng khi biết
đường thẳng đó đi qua 1 điểm và nhận 1 vectơ pháp
tuyến.
- Xác định vectơ pháp tuyến, vectơ chỉ phương của
đường thẳng khi biết các điều kiện cho trước.
Vận dụng
- Viết phương trình tổng quát đường thẳng đi qua 1
điểm và vuông góc với đường thẳng cho trước.
2 (TN)
Câu 21
Câu 22
2 (TN)
Câu 24
Câu 28
TL3a
TL3b
Vị trí tương đốig
giữa 2 đường
thẳng, góc giữa 2
đường thẳng,
khoảng cách từ
một điểm đến một
đường thẳng
Nhận biết:
- Nhận biết vị trí tương đối giữa hai đường thẳng
(dạng phương trình tham số và phương trình tổng
quát).
- Nhận biết công thức tính khoảng cách từ một điểm
đến một đường thẳng.
Thông hiểu
- Xác định được góc giữa hai đường thẳng.
- Xác định được giao điểm hai đường thẳng.
2 (TN)
Câu 23
Câu 26
2 (TN)
Câu 29
Câu 27
Đường tròn trong
mặt phẳng toạ độ
và ứng dụng
Nhận biết:
- Nhận biết điều kiện để phương trình là phương trình
đường tròn.
Thông hiểu:
- Xác định được tâm và bán kính đường tròn biết
phương trình của nó.
- Xác định được phương trình đường tròn biết tâm và
bán kính cho trước.
1 (TN)
Câu 30
3 (TN)
Câu 25
Câu 31
Câu 32
- Xác định đường thẳng tiếp xúc với đường tròn cho
trước
Vận dụng cao:
- Vận dụng kiến thức về phương trình đường thẳng và
phương trình đường tròn để giải bài toán phức hợp,
không quen thuộc.
Ba đường conic
trong mặt phẳng
toạ độ và ứng
dụng
Nhận biết:
- Nhận biết phương trình 3 đường conic.
- Nhận biết các yếu tố trong conic (độ đài trục lớn,
trục bé, tiêu sự của elip, hypebol, tham số tiêu của
parabol, giao điểm với các trục toạ độ)
3 (TN)
Câu 33
Câu 34
Câu 35
Tổng
18 TN 17 TN 3TL 1TL
Tỉ lệ %
36% 34% 25% 5%
Tỉ lệ chung
70% 30%
| 1/17
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT QUẢNG NAM
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG THPT HỒ NGHINH NĂM HỌC 2023 - 2024
(Đề thi có 05 trang)
MÔN TOÁN – Khối lớp 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề 101
Họ và tên học sinh:…………………………. Số báo danh:…………….
I. PHẦN TRẮC NGHIỆM (7.0 ĐIỂM)
Câu 1: Trong mặt phẳng Oxy , cho phương trình chính tắc của parabol là 2
y = 2 px , với p > 0. Khi đó,
parabol có tiêu điểm là: A. p F  ;0 − p p p   . B. F 0; . C. F 0;− .
D. F  ;0 . 2        2   2   2 
Câu 2: Trong mặt phẳng Oxy , phương trình chính tắc của hypebol có dạng là: 2 2 2 2 A. x y + = 1. B. 2 y = px . C. x y − = 1. D. 2 y = 2 px . 2 2 a b 2 2 a b
Câu 3: Giá trị x = 2 là nghiệm của phương trình nào sau đây? A. 2
x − x − 4 = x − 4 . B. x + 2 = 2 3x − 2 . C. x + 2 = x −1 .
D. x −1 = x − 3 .
Câu 4: Điểm nào dưới đây không thuộc đồ thị của hàm số 2 y = 2 − x ? A. (1;− 2) . B. (0;0) . C. ( 1; − 2) . D. (2;−8) .
Câu 5: Đồ thị hàm số bậc hai 2
y = ax + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm A. b I ; ∆   b ∆  b ∆  b ∆ − −     . B. I  ; . C. I −  ; − . D. I −  ; − . 2a 4      a   a 4a   a 4a   2a 2a  x =1− 4t
Câu 6: Trong mặt phẳng Oxy , đường thẳng d : 
có một vectơ chỉ phương là: y = 2 − + 3t     A. u = ( 4; − 3) . B. u = (4;3) . C. u = (3;4) . D. u = (1; 2 − ) .
Câu 7: Tam thức bậc hai nào sau đây có hệ số a = 3;b = 2 − ;c = 7 − ? A. 2 3
− x + 2x + 7 . B. 2 3x + 2x − 7 . C. 2
3x − 2x − 7 . D. 2 3x − 2x + 7 .
Câu 8: Trong mặt phẳng Oxy , đường thẳng ∆ : x + 3y − 2 = 0 song song với đường thẳng có phương trình nào sau đây?
A. 3x − y = 0 .
B. 3x + y − 2 = 0.
C. 2x + 6y +1 = 0 . D. 2
− x − 6y + 4 = 0 .
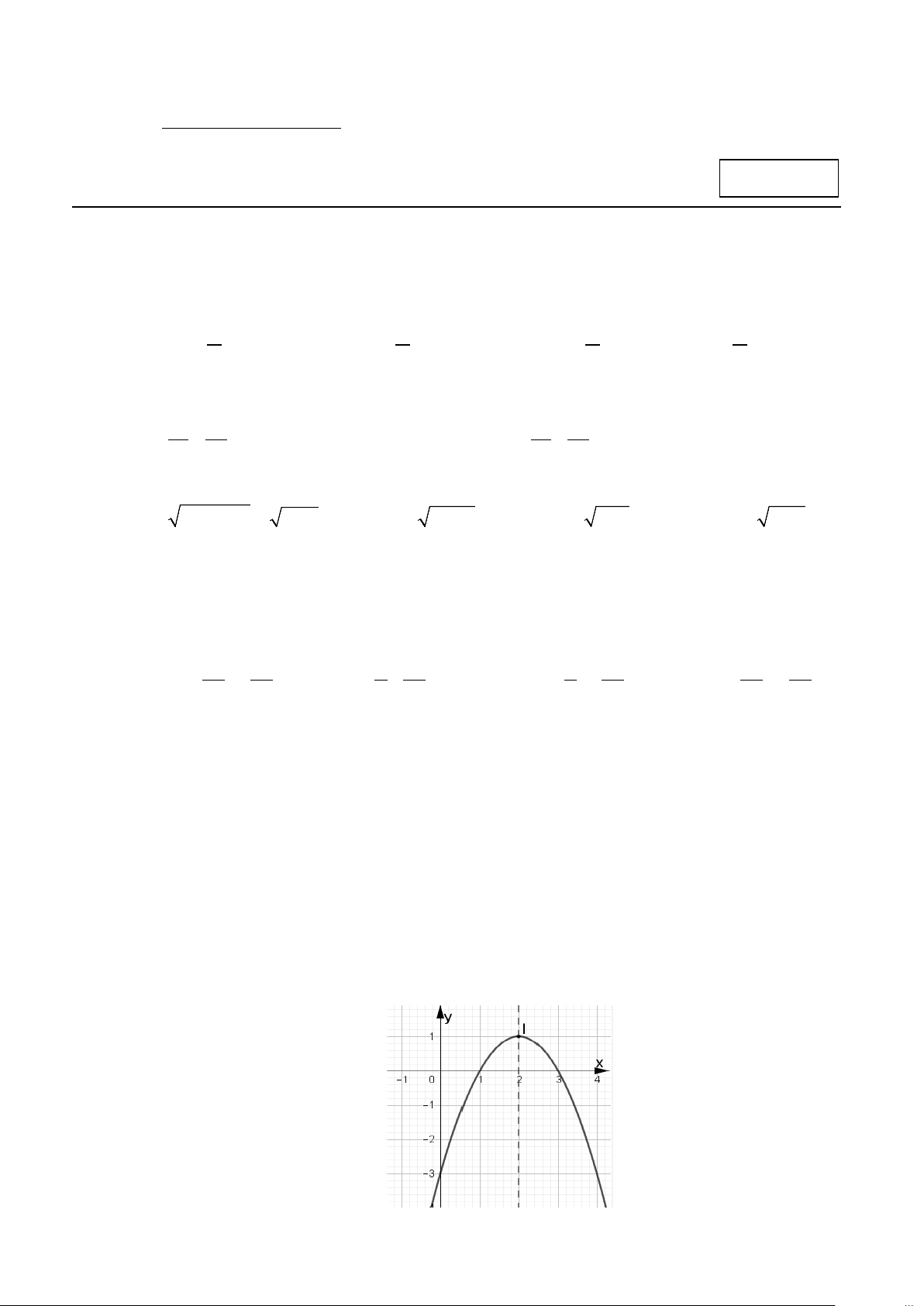
Câu 9: Cho parabol có đồ thị như hình vẽ sau: 1/ 5 – Mã đề 101
Trục đối xứng của parabol là: A. x =1. B. x = 3. C. x = 2. D. y = 2.
Câu 10: Tập nghiệm của phương trình: 2 x − 3 = 1 − là: A. { } 0 . B. { } 2 . C. {2; } 2 − . D. ∅ .
Câu 11: Trong mặt phẳng Oxy , khoảng cách từ điểm M (x ; y đến đường thẳng ∆ : Ax + By + C = 0 0 0 )
được tính bởi công thức: x + y + C
Ax + By + C
A. d (M ,∆) 0 0 = .
B. d (M ,∆) 0 0 = . 2 2 A + B . 2 2 A + B .
Ax + By + C
Ax + By − C
C. d (M ,∆) 0 0 = .
D. d (M ,∆) 0 0 = . 2 2 A + B 2 2 A + B . 2 2
Câu 12: Trong mặt phẳng Oxy , đường elip x + y = 1 có một giao điểm với trục tung là: 16 9 A. 0;  3 . B. 3;  0 . C. (0;4) . D. (4;0) .
Câu 13: Trong mặt phẳng Oxy , cho phương trình 2 2
x + y + 2ax + 2by + c = 0,(a, ,
b c∈) là phương
trình đường tròn. Khi đó a,b,c thỏa mãn điều kiện nào sau đây? A. 2 2
a + b − c > 0 . B. 2 2
a + b − c < 0. C. 2 2
a − b + c < 0. D. 2 2
a − b + c > 0 . . Câu 14: Cho hàm số 2
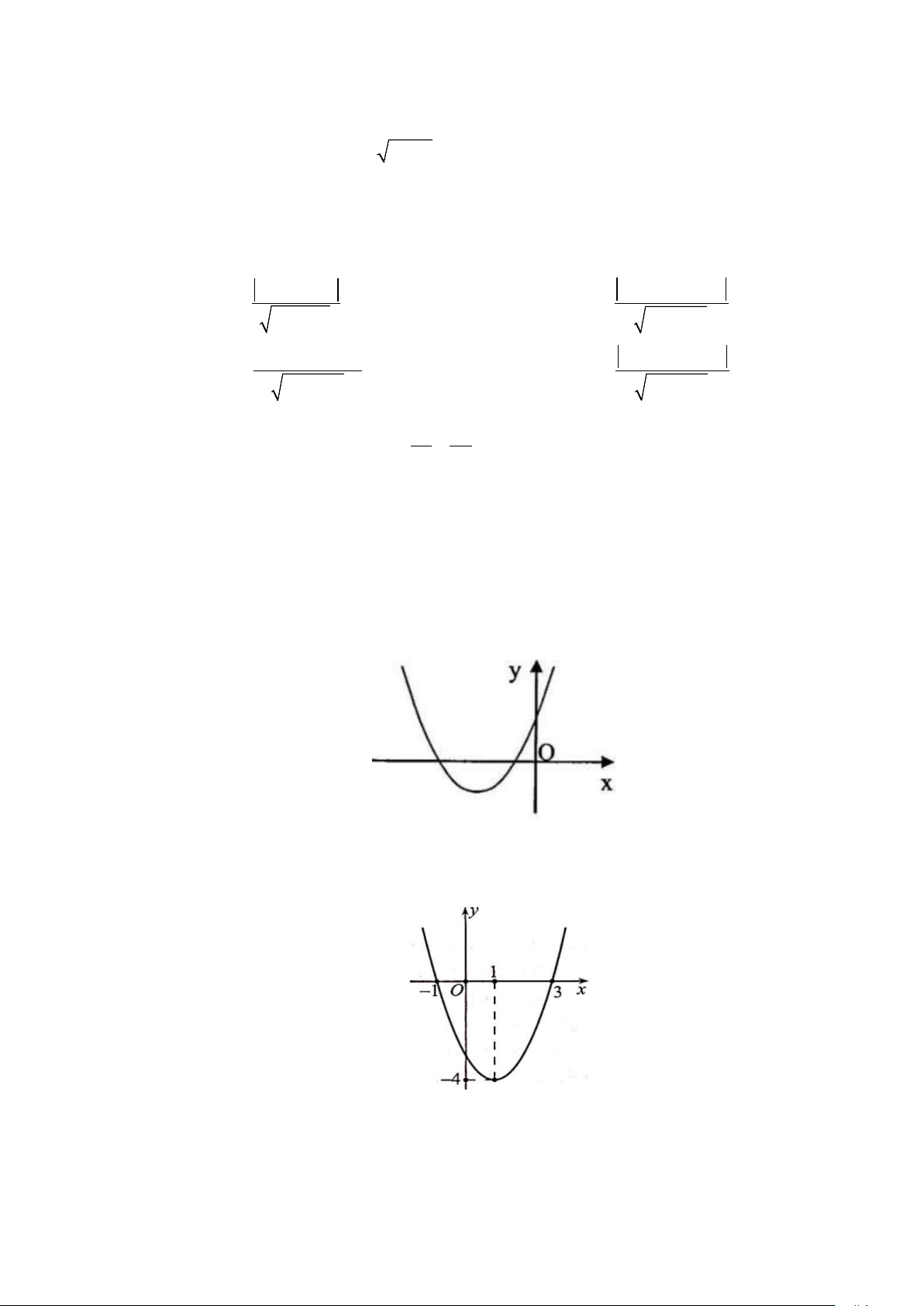
y = ax + bx + c (a ≠ 0) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? A. c = 0. B. a > 0. C. c < 0. D. a < 0.
Câu 15: Cho hàm số bậc hai 2
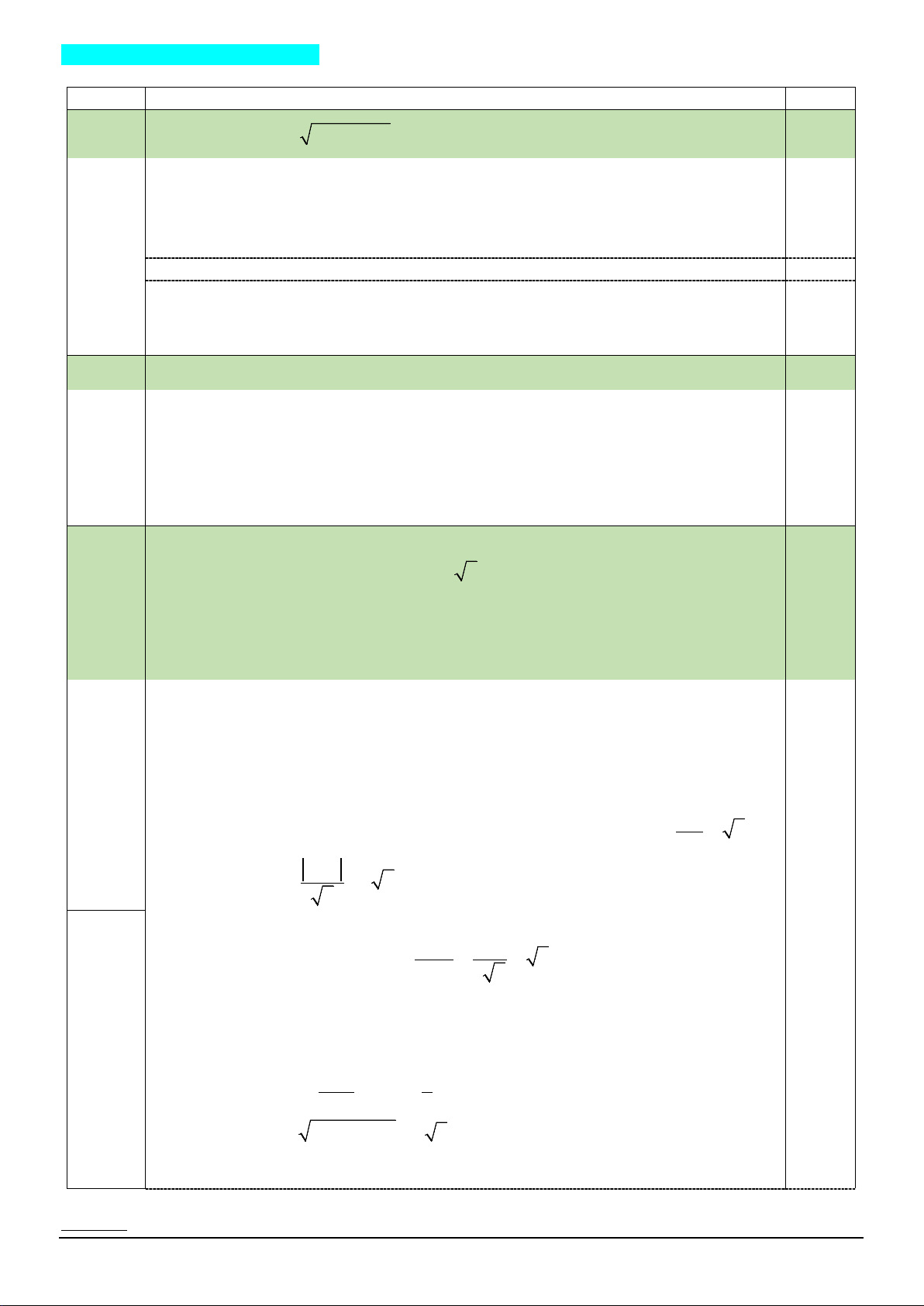
y = ax + bx + c có đồ thị như hình bên dưới.
Hàm số đã cho nghịch biến trên khoảng nào sau đây? A. ( 4; − +∞). B. (0;+∞) . C. (1;+∞) . D. ( ; −∞ 1) .
Câu 16: Hàm số nào dưới đây là hàm số bậc hai 2/ 5 – Mã đề 101 A. 1 3
y = x − 2x +1. B. 1 y = . C. y = 3 − x +1. D. 1 2
y = − x + x −1. 2 2 x + 2x +1 2
Câu 17: Trong mặt phẳng Oxy , đường thẳng (d ) ax + by + c = ( 2 2 :
0, a + b ≠ 0) . Vectơ nào sau đây là
một vectơ pháp tuyến của đường thẳng (d ) ?     A. n = ( ; b −a) . B. n = ( ; a b) . C. n = ( ; b a) . D. n = ( ; a b − ) .
Câu 18: Bảng dưới đây cho biết nồng độ bụi PM 2.5trong không khí theo thời gian trong ngày
25 − 3− 2021tại một trạm quan trắc ở Thủ đô Hà Nội:
Nồng độ bụi PM 2.5 tại thời điểm 8 giờ là: A. 64,58. B. 74,27. C. 57,9. D. 81,78.
Câu 19: Tìm tập xác định D của hàm số f ( x ) 2x + 3 = . x + 1 A. D =  .
B. D = ( 0;+∞ ). C. D = ( ;0 −∞ ).
D. D =  \ {− } 1 .
Câu 20: Trong mặt phẳng Oxy , đường tròn 2 2
x + y −1 = 0 tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?
A. x + y = 0 .
B. 3x − 4y + 5 = 0 . C. 3x + 4y −1 = 0.
D. x + y −1 = 0 .
Câu 21: Trong mặt phẳng Oxy , tính góc giữa hai đường thẳng ∆ : x − 3y + 2 = 0 và ∆′: x + 3y −1= 0 A. 90 . B. 60 . C. 30 . D. 120 . 
Câu 22: Trong mặt phẳng Oxy , đường thẳng d có một vectơ chỉ phương là u = (3; 4 − ) . Đường thẳng
∆ vuông góc với d có một vectơ pháp tuyến là:     A. n = 4; − 3 . n = 3; 4 − . n = 4;3 . n = 3;4 . 2 ( ) B. 4 ( ) C. 1 ( ) D. 3 ( )
Câu 23: Tập nghiệm của bất phương trình 2
−x + 3x − 2 ≥ 0 là: A. [ 1; − 2]. B. [ 2; − ] 1 . C. (1;2) . D. [1;2].
Câu 24: Cho tam thức f (x) 2
= ax + bx + c (a ≠ 0), 2
∆ = b − 4ac . Để f ( x) ≤ 0 với x ∀ ∈  thì a < 0 a > 0 a < 0 a ≤ 0 A.  . B.  . C.  . D.  . ∆ ≥ 0 ∆ ≤ 0 ∆ ≤ 0 ∆ < 0 Câu 25: Cho parabol 2
y = x + bx + c có tọa độ đỉnh I(1;2) . Mệnh đề nào sau đây đúng? A. 2
x + bx + c > 0 với x ∀ ∈  . B. 2
x + bx + c < 0 với x ∀ ∈  . C. 2
x + bx + c ≤ 0 với x ∀ ∈  . D. 2
x + bx + c ≥ 3 với x ∀ ∈  .
Câu 26: Trong mặt phẳng Oxy , đường tròn tâm I(3; 7
− ) , bán kính R = 3 có phương trình là:
A. (x + )2 + ( y − )2 3 7 = 9.
B. (x + )2 + ( y + )2 3 7 = 9. 3/ 5 – Mã đề 101
C. (x − )2 + ( y + )2 3 7 = 9 .
D. (x − )2 + ( y + )2 3 7 = 3 .
Câu 27: Trong mặt phẳng Oxy , tọa độ giao điểm của hai đường thẳng 3x + 4y − 7 = 0 và
4x − 3y − 26 = 0 là: A. ( 5; − 2 − ) . B. (5;2) . C. (5; 2 − ). D. ( 5; − 2) . .
Câu 28: Trong các tam thức sau, tam thức nào luôn âm với mọi x∈ ? A. f (x) 2
= −x − 3x − 4 . B. f (x) 2
= −x − 3x + 4 . C. f (x) 2
= −x − 4x − 4 . D. f (x) 2
= x − 3x + 4 .
Câu 29: Bình phương hai vế của phương trình 2 2
x − x = 3x + 2x −1 và rút gọn ta được phương trình nào dưới đây? A. 2
2x + 3x −1 = 0. B. x −1 = 0.
C. −x −1 = 0. D. 2 3x −1 = 0.
Câu 30: Số nghiệm nguyên dương của phương trình x −1 = x −3 là: A. 1. B. 3. C. 2 . D. 0 . 
Câu 31: Trong mặt phẳng Oxy, đường thẳng đi qua A( 1;
− 2) , nhận n = (2; 4
− ) làm véctơ pháp tuyến có phương trình là:
A. x − 2y − 4 = 0 .
B. x + y + 4 = 0 .
C. −x + 2y − 4 = 0 .
D. x − 2y + 5 = 0.
Câu 32: Hàm số y = f (x) được cho bằng bảng sau:
Tập giá trị của hàm số là:
A. T = {1;2;3;4;5;6; } 7 .
B. T = {3;4;5;6;7;8; } 9 . C. T =  .
D. T = {3;4;5;6;7;8;9;1 } 0 .
Câu 33: Trong mặt phẳng Oxy , cho đường tròn (C) (x + )2 + ( y − )2 : 1
3 = 25. Trong các mệnh đề sau
đây, phát biểu nào sai?
A. (C) có tâm A(1; 3).
B. (C) có bán kính R = 5.
C. (C) có tâm I ( 1; − 3).
D. (C) đi qua điểm B(4;3).
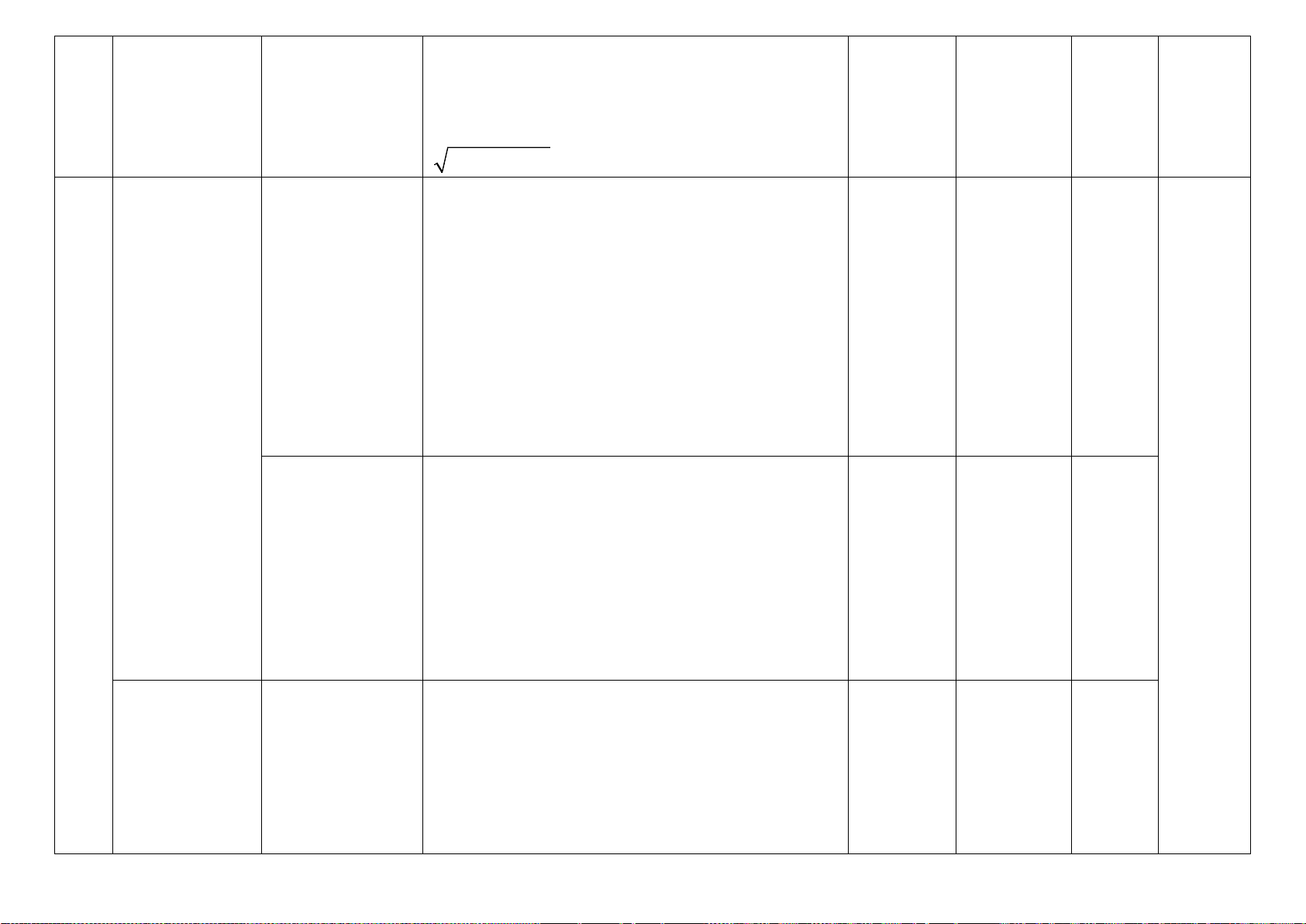
Câu 34: Parabol dưới đây là đồ thị của hàm số nào? A. 2
y = x + 2x − 2 . B. 2
y = x − 2x −1. C. 2
y = x + 2x −1. D. 2
y = −x − 2x +1. 4/ 5 – Mã đề 101
Câu 35: Bảng xét dấu nào dưới đây là bảng xét dấu của tam thức bậc hai 2
f (x) = x − x − 6 ? A. . B. . C. . D. .
II. PHẦN TỰ LUẬN (3.0 ĐIỂM ) Câu 1 (1 điểm). Giải phương trình: 2
2x + x + 3 =1− x Câu 2. (1 điểm) Cho hàm số 2
y = x + 2x −8 có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho. Câu 3: (1 điểm)
Trong mặt phẳng hệ toạ độ Oxy , cho đường thẳng ∆ : x + y = 0. Đường tròn (C) cắt ∆ tại hai điểm ,
A B sao cho AB = 2 6 . Các tiếp tuyến của (C) tại hai điểm ,
A B cắt nhau tại điểm M (0; 6 − ).
a. Viết phương trình đường thẳng d qua M và vuông góc với ∆ .
b. Viết phương trình đường tròn (C).
---------------------------HẾT --------------------- 5/ 5 – Mã đề 101 SỞ GD&ĐT QUẢNG NAM
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG THPT HỒ NGHINH NĂM HỌC 2023 - 2024
(Đề thi có 05 trang)
MÔN TOÁN – Khối lớp 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề 102
Họ và tên học sinh:………………………….. Số báo danh:…………………...
I. PHẦN TRẮC NGHIỆM (7.0 ĐIỂM)
Câu 1: Trong mặt phẳng Oxy , phương trình chính tắc của hypebol có dạng là: 2 2 2 2 A. x y − = 1. B. x y + = 1. C. 2 y = px . D. 2 y = 2 px . 2 2 a b 2 2 a b
Câu 2: Điểm nào dưới đây không thuộc đồ thị của hàm số 2 y = 2 − x ? A. (0;0) . B. (2;−8) . C. ( 1; − 2) . D. (1;− 2) .
Câu 3: Hàm số nào dưới đây là hàm số bậc hai A. 1 3
y = x − 2x +1. B. 1 2
y = − x + x −1. C. y = 3 − x +1. D. 1 y = . 2 2 2 x + 2x +1
Câu 4: Cho parabol có đồ thị như hình vẽ sau:
Trục đối xứng của parabol là: A. y = 2. B. x = 3. C. x =1. D. x = 2.
Câu 5: Trong mặt phẳng Oxy , đường thẳng ∆ : x + 3y − 2 = 0 song song với đường thẳng có phương trình nào sau đây?
A. 3x − y = 0 . B. 2
− x − 6y + 4 = 0 . C. 3x + y − 2 = 0 .
D. 2x + 6y +1 = 0 .
Câu 6: Giá trị x = 2 là nghiệm của phương trình nào sau đây?
A. x −1 = x − 3 .
B. x + 2 = 2 3x − 2 .
C. x + 2 = x −1 . D. 2
x − x − 4 = x − 4 . Câu 7: Cho hàm số 2
y = ax + bx + c (a ≠ 0) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? 1 / 5 – Mã đề 102 A. a > 0. B. a < 0. C. c = 0. D. c < 0.
Câu 8: Tam thức bậc hai nào sau đây có hệ số a = 3;b = 2 − ;c = 7 − ? A. 2
3x − 2x − 7 . B. 2 3x + 2x − 7 . C. 2 3
− x + 2x + 7 . D. 2 3x − 2x + 7 .
Câu 9: Trong mặt phẳng Oxy , đường thẳng (d ) ax + by + c = ( 2 2 :
0, a + b ≠ 0) . Vectơ nào sau đây là
một vectơ pháp tuyến của đường thẳng (d ) ?     A. n = ( ; b a) . B. n = ( ; a b) .
C. n = (a; b − ) . D. n = ( ; b −a) . 2 2
Câu 10: Trong mặt phẳng Oxy , đường elip x + y = 1 có một giao điểm với trục tung là: 16 9 A. (0;4) . B. (4;0) . C. 3;  0 . D. 0;  3 . x =1− 4t
Câu 11: Trong mặt phẳng Oxy , đường thẳng d : 
có một vectơ chỉ phương là: y = 2 − + 3t     A. u = (3;4) . B. u = (1; 2 − ) . C. u = ( 4; − 3) . D. u = (4;3) .
Câu 12: Bảng dưới đây cho biết nồng độ bụi PM 2.5trong không khí theo thời gian trong ngày
25 − 3− 2021tại một trạm quan trắc ở Thủ đô Hà Nội:
Nồng độ bụi PM 2.5 tại thời điểm 8 giờ là: A. 57,9. B. 81,78. C. 74,27. D. 64,58.
Câu 13: Trong mặt phẳng Oxy , cho phương trình 2 2
x + y + 2ax + 2by + c = 0,(a, ,
b c∈) là phương
trình đường tròn. Khi đó a,b,c thỏa mãn điều kiện nào sau đây? A. 2 2
a + b − c < 0. B. 2 2
a − b + c < 0. C. 2 2
a − b + c > 0 . . D. 2 2
a + b − c > 0 .
Câu 14: Cho hàm số bậc hai 2
y = ax + bx + c có đồ thị như hình bên dưới. 2 / 5 – Mã đề 102
Hàm số đã cho nghịch biến trên khoảng nào sau đây? A. (0;+∞) . B. (1;+∞) . C. ( ; −∞ 1) . D. ( 4; − +∞).
Câu 15: Trong mặt phẳng Oxy , cho phương trình chính tắc của parabol là 2
y = 2 px , với p > 0. Khi đó,
parabol có tiêu điểm là: A. 0; p F   − p p p   .
B. F  ;0 . C. F 0; . D. F  −  ;0 . 2        2   2   2 
Câu 16: Tập nghiệm của phương trình: 2 x − 3 = 1 − là: A. { } 0 . B. { } 2 . C. ∅ . D. {2; } 2 − .
Câu 17: Đồ thị hàm số bậc hai 2
y = ax + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm A. b I ; ∆   b ∆  b ∆  b ∆ − −     . B. I −  ; − . C. I −  ; − . D. I  ; . a 4      a   2a 4a   2a 2a   a 4a
Câu 18: Trong mặt phẳng Oxy , khoảng cách từ điểm M (x ; y đến đường thẳng ∆ : Ax + By + C = 0 0 0 )
được tính bởi công thức:
Ax + By + C x + y + C
A. d (M ,∆) 0 0 = .
B. d (M ,∆) 0 0 = . 2 2 A + B 2 2 A + B .
Ax + By + C
Ax + By − C
C. d (M ,∆) 0 0 = .
D. d (M ,∆) 0 0 = . 2 2 A + B . 2 2 A + B .
Câu 19: Trong mặt phẳng Oxy , đường tròn 2 2
x + y −1 = 0 tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?
A. x + y −1 = 0 .
B. 3x + 4y −1 = 0.
C. 3x − 4y + 5 = 0 . D. x + y = 0 . 
Câu 20: Trong mặt phẳng Oxy , đường thẳng d có một vectơ chỉ phương là u = (3; 4 − ) . Đường thẳng
∆ vuông góc với d có một vectơ pháp tuyến là:     A. n = 4;3 . n = 3; 4 − . n = 4; − 3 . n = 3;4 . 1 ( ) B. 4 ( ) C. 2 ( ) D. 3 ( )
Câu 21: Tìm tập xác định D của hàm số f ( x ) 2x + 3 = . x + 1
A. D = ( 0;+∞ ). B. D =  .
C. D =  \ {− } 1 . D. D = ( ;0 −∞ ).
Câu 22: Số nghiệm nguyên dương của phương trình x −1 = x −3 là: A. 1. B. 3. C. 0 . D. 2 .
Câu 23: Trong mặt phẳng Oxy , đường tròn tâm I(3; 7
− ) , bán kính R = 3 có phương trình là: 3 / 5 – Mã đề 102
A. (x + )2 + ( y + )2 3 7 = 9.
B. (x − )2 + ( y + )2 3 7 = 3.
C. (x − )2 + ( y + )2 3 7 = 9 .
D. (x + )2 + ( y − )2 3 7 = 9.
Câu 24: Bảng xét dấu nào dưới đây là bảng xét dấu của tam thức bậc hai 2
f (x) = x − x − 6 ? A. . B. . C. . D. .
Câu 25: Cho tam thức f (x) 2
= ax + bx + c (a ≠ 0), 2
∆ = b − 4ac . Để f ( x) ≤ 0 với x ∀ ∈  thì a < 0 a ≤ 0 a > 0 a < 0 A.  . B.  . C.  . D.  . ∆ ≥ 0 ∆ < 0 ∆ ≤ 0 ∆ ≤ 0
Câu 26: Bình phương hai vế của phương trình 2 2
x − x = 3x + 2x −1 và rút gọn ta được phương trình nào dưới đây? A. 2
2x + 3x −1 = 0. B. x −1 = 0. C. 2 3x −1 = 0.
D. −x −1 = 0.
Câu 27: Trong mặt phẳng Oxy , cho đường tròn (C) (x + )2 + ( y − )2 : 1
3 = 25. Trong các mệnh đề sau
đây, phát biểu nào sai?
A. (C) có tâm A(1; 3).
B. (C) có tâm I ( 1; − 3).
C. (C) có bán kính R = 5.
D. (C) đi qua điểm B(4;3). 
Câu 28: Trong mặt phẳng Oxy, đường thẳng đi qua A( 1;
− 2) , nhận n = (2; 4
− ) làm véctơ pháp tuyến có phương trình là:
A. x + y + 4 = 0 .
B. −x + 2y − 4 = 0 .
C. x − 2y − 4 = 0 .
D. x − 2y + 5 = 0.
Câu 29: Trong mặt phẳng Oxy , tọa độ giao điểm của hai đường thẳng 3x + 4y − 7 = 0 và
4x − 3y − 26 = 0 là: A. ( 5; − 2 − ) . B. (5; 2 − ). C. (5;2) . D. ( 5; − 2) . .
Câu 30: Parabol dưới đây là đồ thị của hàm số nào? A. 2
y = x + 2x − 2 . B. 2
y = x − 2x −1. C. 2
y = x + 2x −1. D. 2
y = −x − 2x +1.
Câu 31: Trong mặt phẳng Oxy , tính góc giữa hai đường thẳng ∆ : x − 3y + 2 = 0 và ∆′: x + 3y −1= 0 A. 30 . B. 60 . C. 120 . D. 90 . 4 / 5 – Mã đề 102 Câu 32: Cho parabol 2
y = x + bx + c có tọa độ đỉnh I(1;2) . Mệnh đề nào sau đây đúng? A. 2
x + bx + c > 0 với x ∀ ∈  . B. 2
x + bx + c ≥ 3 với x ∀ ∈  . C. 2
x + bx + c < 0 với x ∀ ∈  . D. 2
x + bx + c ≤ 0 với x ∀ ∈  .
Câu 33: Trong các tam thức sau, tam thức nào luôn âm với mọi x∈ ? A. f (x) 2
= −x − 4x − 4 . B. f (x) 2
= −x − 3x + 4 . C. f (x) 2
= x − 3x + 4 . D. f (x) 2
= −x − 3x − 4 .
Câu 34: Hàm số y = f (x) được cho bằng bảng sau:
Tập giá trị của hàm số là:
A. T = {3;4;5;6;7;8;9;1 } 0 .
B. T = {3;4;5;6;7;8; } 9 . C. T =  .
D. T = {1;2;3;4;5;6; } 7 .
Câu 35: Tập nghiệm của bất phương trình 2
−x + 3x − 2 ≥ 0 là: A. [ 2; − ] 1 . B. [ 1; − 2]. C. (1;2) . D. [1;2].
II. PHẦN TỰ LUẬN (3.0 ĐIỂM ) Câu 1: (1 điểm)
Giải phương trình: 2
2x − 5x − 9 = x −1 Câu 2: (1 điểm) Cho hàm số 2
y = −x + 4x + 5 có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho. Câu 3: (1 điểm)
Trong mặt phẳng hệ toạ độ Oxy , cho đường thẳng ∆ : x − y = 0. Đường tròn (C) cắt ∆ tại hai điểm ,
A B sao cho AB = 4 2 . Các tiếp tuyến của (C) tại hai điểm ,
A B cắt nhau tại điểm M (0;8).
a. Viết phương trình đường thẳng d qua M và vuông góc với ∆ .
b. Viết phương trình đường tròn (C).
-------------------HẾT------------------------- 5 / 5 – Mã đề 102
SỞ GD&ĐT TỈNH QUẢNG NAM
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA KÌ II. NĂM HỌC: 2023 - 2024
TRƯỜNG THPT HỒ NGHINH MÔN: TOÁN 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề) I/ TRẮC NGHIỆM
Đề\câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
101 D C B C A A C C C D B A A B D D B C D B B B D C A C C A A A D B A C D
102 A C B D D B A A B D C A D C B C B C C B C A C A D A A D B C B A D B D
103 C C B B A B C C D D B A A D D A C B D C A B C D B D D B A A B A C C D
104 B C D A D D C D A C A B A C B D C B C D C C B D A B A D B B D A B A C
105 D A B B C A A D C C B B D D B A B C A A B A C C D A C B B C D B A D D
106 A D B D A B A D C A C C D A C D B B C B A D B D A D A B A D C D C B C
107 A B D D B B C A C A A B D D C B C D B B C C A C D B B A A D D A D A C
108 C B A D D B D C B A D A C C B B A A C A B A B C D D C A B A D D B C B Trang 1/3
II. Phần tự luận. (3,0 điểm)
Gồm các mã đề 102; 104;106;108 Câu Nội dung yêu cầu Điểm Câu 1: (1,0đ)
Giải phương trình: 2
2x − 5x − 9 = x −1
Bình phương hai vế của phương trình ta được: 2 2
2x −5x −9 = x − 2x +1. 0,25
Sau khi thu gọn ta được 2
x − 3x −10 = 0 . 0,25
Từ đó tìm được x = 2 − hoặc x = 5. 0,25
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 5 thỏa mãn. 0,25
Vậy nghiệm của phương trình đã cho là x = 5. Câu 2: Cho hàm số 2
y = −x + 4x + 5 có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho. (1,0đ)
Xác định hệ số a, b, c
Xác định được trục đối xứng x = 2 0,25 Toạ độ đỉnh I (2;9) 0,25
Lập bảng giá trị các điểm 0,25 Vẽ đúng Parabol 0,25 Câu 3
Trong mặt phẳng hệ toạ độ Oxy , cho đường thẳng ∆ : x − y = 0. Đường tròn (C) cắt ∆ tại hai điểm ,
A B sao cho AB = 4 2 . Các tiếp tuyến của (C) tại hai điểm ,
A B cắt nhau tại điểm M (0;8). (1,0đ)
a. Viết phương trình đường thẳng d qua M và vuông góc với ∆ .
b. Viết phương trình đường tròn (C). 
a. Đường thẳng d vuông góc với ∆ nên nhận VTPT n − của ∆ làm VTCP. ∆(1; 1)  0,25
Suy ra 1 vectơ pháp tuyến của d là n . d (1;1)
Phương trình đường thẳng d: 1(x − 0) +1(y −8) = 0 ⇔ x + y −8 = 0 . 0,25
b. Giả sử đường tròn (C) có tâm I .
Gọi H = IM ∩ AB . Suy ra H là trung điểm của , = AB AB AH = 2 2 . 2 −
MH = d (M ∆) 0 8 , ⇔ = 4 2 2 0,25
Tam giác AIM vuông tại A , AH ⊥ IM nên có: 2 2 AH 8
AH = HM.IH ⇔ IH = = = 2 HM 4 2
H là giao điểm của 2 đường thẳng IM và AB (trong đó AB ≡ ∆, IM ≡ d ). Toạ độ x − y = 0 x = 4
H là nghiệm của hpt:  ⇔  ⇒ H (4;4)
x + y − 8 = 0 y = 4   Ta có HM 1 IH =
⇒ IH = HM ⇒ I (5;3) 4 4 2 2
R = IA = AH + IH = 10
Vậy phương trình đường tròn (C) là: (x − )2 + ( y − )2 5 3 =10. 0.25 Trang 1/3
Gồm các mã đề 101; 103;105;107 Câu Nội dung yêu cầu Điểm Câu 1: (1,0đ)
Giải phương trình: 2
2x + x + 3 =1− x
Bình phương hai vế của phương trình ta được 2 2
2x + x + 3 =1− 2x + x . 0,25
Sau khi thu gọn ta được 2
x + 3x + 2 = 0 . 0,25
Từ đó tìm được x = 1 − hoặc x = 2 − 0,25
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x = 1 − hoặc x = 2 − thỏa mãn. 0,25
Vậy tập nghiệm của phương trình đã cho là S = { 1; − − } 2 . Câu 2: Cho hàm số 2
y = x + 2x −8 có đồ thị là một Parabol (P). Vẽ đồ thị hàm số đã cho. (1,0đ)
Xác định hệ số a, b, c
Xác định được trục đối xứng x = - 1 0,25
Toạ độ đỉnh I (-1;-9) 0,25
Lập bảng giá trị các điểm 0,25 Vẽ đúng Parabol 0,25 Câu 3
Trong mặt phẳng hệ toạ độ Oxy , cho đường thẳng ∆ : x + y = 0. Đường tròn (C) cắt ∆ tại hai điểm ,
A B sao cho AB = 2 6 . Các tiếp tuyến của (C) tại hai điểm ,
A B cắt nhau tại điểm M (0; 6 − ). (1,0đ)
a. Viết phương trình đường thẳng d qua M và vuông góc với ∆ .
b. Viết phương trình đường tròn (C). 
a. Đường thẳng d vuông góc với ∆ nên nhận VTPT n của ∆ làm VTCP. ∆(1;1)  0,25
Suy ra 1 vectơ pháp tuyến của d là n − . d (1; 1)
Phương trình đường thẳng d: 1(x − 0) −1(y + 6) = 0 ⇔ x − y − 6 = 0 . 0,25
b. Giả sử đường tròn (C) có tâm I .
Gọi H = IM ∩ AB . Suy ra H là trung điểm của , AB AB AH = = 6 . 2 −
MH = d (M ∆) 0 6 , ⇔ = 3 2 2 0,25
Tam giác AIM vuông tại A , AH ⊥ IM nên có: 2 2 AH 6
AH = HM.IH ⇔ IH = = = 2 HM 3 2
H là giao điểm của 2 đường thẳng IM và AB (trong đó AB ≡ ∆, IM ≡ d ). x + y = 0 x = 3
Toạ độ H là nghiệm của hpt:  ⇔  ⇒ H (3; 3 − )
x − y − 6 = 0 y = 3 −   Ta có HM 1 IH =
⇒ IH = HM ⇒ I (4; 2 − ) 3 3 2 2
R = IA = AH + IH = 2 2
Vậy phương trình đường tròn (C) là: (x − )2 + ( y + )2 4 2 = 8 . 0.25
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa của câu đó. Trang 2/3
TRƯỜNG THPT HỒ NGHINH
MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ II
MÔN: TOÁN LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận: 4 câu (30%)
Mức độ đánh giá TT Chương/Chủ đề
Nội dung/Đơn vị kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao Tổng % điểm
TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Khái niệm cơ bản về hàm số và đồ thị 3 2 10%
Hàm số, đồ Hàm số bậc hai, đồ thị hàm số bậc 1 thị và ứng hai và ứng dụng 4 2 1 22%
dụng (12 tiết) Dấu của tam thức bậc hai. Bất
phương trình bậc hai một ẩn 1 4 10%
Phương trình quy về phương trình bậc hai 2 2 1 18%
Đường thẳng trong mặt phẳng toạ
độ. Phương trình tổng quát và
phương trình tham số của đường 2 2 1 13% thẳng. PP tọa độ
Vị trí tương đối giữa 2 đường thẳng, 1 2 trong mặt
góc giữa 2 đường thẳng, khoảng phẳng (11
cách từ một điểm đến một đường 2 2 8% tiết) thẳng
Đường tròn trong mặt phẳng toạ độ và ứng dụng 1 3 13%
Ba đường conic trong mặt phẳng toạ độ và ứng dụng 3 6% Tổng 18 17 3 1 Tỉ lệ (%) 36 34 25 5 100% Tỉ lệ chung (%) 70 30 100%
II. BẢNG ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ II - MÔN TOÁN - LỚP 10 Nội dung/Đơn
Số câu hỏi theo mức độ nhận thức
STT Chương/chủ đề vị kiến thức
Mức độ kiểm tra, đánh giá NB TH VD VDC Nhận biết:
- Nhận biết giá trị của hàm số dựa vào bảng giá trị. 3 (TN) 2 (TN)
- Nhận biết được khoảng đồng biến và nghịch biến
Khái niệm cơ bản về Câu 1, Câu 4,
dựa vào đồ thị hàm số
hàm số và đồ thị
- Nhận điểm có thuộc/ không thuộc đồ thị Câu 2, Câu 5 Thông hiểu: Câu 3
- Tìm được tập xác định, tập giá trị của hàm số. Nhận biết
- Nhận biết được hàm số bậc hai. 4 (TN)
- Nhận biết toạ độ đỉnh, trục đối xứng, bề lõm của Hàm số bậc hai, parabol. Câu 6, 2 (TN)
đồ thị hàm số bậc Thông hiểu: Câu 7, Câu 10, TL2
- Xác định được các tính chất của đồ thị hàm số bậc HÀM SỐ, ĐỒ hai và ứng dụng hai. Câu 8, Câu 11 THỊ
- Nhận diện được hàm số bậc hai từ đồ thị 1 Câu 9 VÀ ỨNG Vận dụng: DỤNG
-Vẽ đồ thị hàm số bậc hai. Nhận biết
- Nhận biết hệ số a, b, c của tam thức bậc hai cho 4 (TN) trước.
Dấu của tam thức Thông hiểu 1 (TN) Câu 12, bậc hai. Bất
- Xác định dấu của tam thức bậc hai. Câu 13, Câu 14 phương trình bậc
+ Tìm được các khoảng hoặc nửa khoảng để tam thức hai một ẩn
bậc hai nhận giá trị dương (âm, không dương, không Câu 15, âm, ...). Câu 16
+ Tìm tập nghiệm của bpt bậc 2
+ Lập bảng xét dấu tam thức bậc hai cho trước.
Phương trình quy Nhận biết 2 (TN) 2 (TN) TL1 về phương trình
- Nhận biết nghiệm của phương trình quy về phương bậc hai trình bậc hai Câu 17 Câu 19 Thông hiểu
-Biến đổi phương trình quy về phương trình bậc hai Câu 18 Câu 20
- Tìm nghiệm phương trình quy về phương trình bậc hai Vận dụng:
Giải phương trình dạng: 2
ax + bx + c = dx + e Nhận biết
- Nhận biết dạng PTTQ của đường thẳng – Nhận biết
vectơ pháp tuyến, vectơ chỉ phương của đường thẳng 2 (TN) 2 (TN)
Đường thẳng trong khi biết phương trình.
mặt phẳng toạ độ. Thông hiểu Câu 21 Câu 24
Phương trình tổng - Xác định được PTTQ của đường thẳng khi biết Câu 22 Câu 28 TL3a quát và phương
đường thẳng đó đi qua 1 điểm và nhận 1 vectơ pháp trình tham số của tuyến.
đường thẳng.
- Xác định vectơ pháp tuyến, vectơ chỉ phương của PHƯƠNG
đường thẳng khi biết các điều kiện cho trước. PHÁP TỌA ĐỘ Vận dụng
- Viết phương trình tổng quát đường thẳng đi qua 1 TRONG MẶT
điểm và vuông góc với đường thẳng cho trước. PHẲNG Nhận biết:
- Nhận biết vị trí tương đối giữa hai đường thẳng 2
Vị trí tương đốig giữa 2 đường
(dạng phương trình tham số và phương trình tổng 2 (TN) 2 (TN) thẳng, góc giữa 2 quát). đường thẳng,
- Nhận biết công thức tính khoảng cách từ một điểm Câu 23 Câu 29
đến một đường thẳng. khoảng cách từ Câu 26 Câu 27
một điểm đến một Thông hiểu
đường thẳng
- Xác định được góc giữa hai đường thẳng.
- Xác định được giao điểm hai đường thẳng. Nhận biết:
- Nhận biết điều kiện để phương trình là phương trình 3 (TN)
Đường tròn trong đường tròn. 1 (TN) TL3b
mặt phẳng toạ độ Thông hiểu: Câu 25
và ứng dụng
- Xác định được tâm và bán kính đường tròn biết Câu 30 phương trình của nó. Câu 31
- Xác định được phương trình đường tròn biết tâm và bán kính cho trước. Câu 32
- Xác định đường thẳng tiếp xúc với đường tròn cho trước
Vận dụng cao:
- Vận dụng kiến thức về phương trình đường thẳng và
phương trình đường tròn để giải bài toán phức hợp, không quen thuộc. Nhận biết: 3 (TN) Ba đường conic
- Nhận biết phương trình 3 đường conic. trong mặt phẳng
- Nhận biết các yếu tố trong conic (độ đài trục lớn, Câu 33 toạ độ và ứng
trục bé, tiêu sự của elip, hypebol, tham số tiêu của Câu 34 dụng
parabol, giao điểm với các trục toạ độ) Câu 35 Tổng 18 TN 17 TN 3TL 1TL Tỉ lệ % 36% 34% 25% 5% Tỉ lệ chung 70% 30%
Document Outline

  • MÃ ĐỀ 101
  • MÃ ĐỀ 102
  • HƯỚNG DẪN CHẤM KIỂM TRA GHK2_TOÁN 10
  • MA TRẬN - ĐẶC TẢ GK2 - TOÁN 10