Đề thi giữa học kỳ I năm học 2017 – 2018 môn Toán 12 trường THPT Tây Hồ – Hà Nội

TRƯỜNG THPT TÂY HỒ
ĐỀ THI GIỮA HỌC KỲ I NĂM HỌC 2017 - 2018 ĐỀ GỐC Môn thi: TOÁN
Thời gian làm bài: 60 phút, không kể thời gian giao đề 3x  1
Câu 1. Hàm số y  có đa ̣o hàm là: x  2  5  7 5 7 A) y' B) y' C) y' D) y' 2
( x  2) 2
( x  2) 2
( x  2) 2
( x  2) 1
Câu 2. Tâ ̣p xác đi ̣nh D của hàm số f (x)  x  1  là: x  4
A) D  1; 
B) D  1;  \ 4 
C) D  1 ( ; )
D) D  (4; )
Câu 3. Gọi d là tiếp tuyến của đồ thị hàm số y   x3  x tại điểm M(2;8) . Hê ̣ số góc của d bằng: A)  11 B) 6 C) 11 D)  12 Câu 4. Hàm số 4
y  x  2 2
x  1 nghich biến trên khoảng nào sau đây: A) (1;0); 1 ( ; )
B) (1;0); (0; ) 1
C) ( ; ) 1 ; (0; ) 1
D) ( ; ) Câu 5. Hàm số 3
y   x  3 2
x  1 đồng biến trên khoảng: A) ( ; ) 1 B) (0;2) C) (2; )
D) ( ; ) 1
Câu 6. Tı̀m các giá tri ̣ của tham số m để hàm số 3 y   x  2 2
x  mx  2 nghịch biến trên ( ; ) 3
A) m  4
B) m  4
C) m  4
D) m  4 2  3 Câu 7. Cho hàm số x y 
. Chọn phát biểu đúng trong các phát biểu sau. 4  x
A) Đồng biến trên R
B) Đồng biến trên từng khoảng xác định
C) Nghịch biến trên từng khoảng xác định
D) Luôn giảm trên R
Câu 8. Tı̀m tất cả các giá tri ̣ của tham số m để hàm số y  x3  x2  (m  )
1 x  2m nghi ̣ch biến trên
khoảng (0; )
A) m  1
B) m  1
C) m  3
D) m  3 1
Câu 9. Tìm tất cả các giá tri ̣ của tham số m để hàm số 3 2 y 
x  mx  ( 2
m  m  )
1 x  1 đạt cực đại tại 3
điểm có hoành độ bằng 1.
A) m  0
B) m  1
C) m  2
D) m  3
Câu 10. Khẳng định nào sau đây là đúng về hàm số 4
y  x  4 2 x  2
A) Hàm số đa ̣t cực tiểu ta ̣i x  0
B) Hàm số có cực đa ̣i và cực tiểu
C) Hàm số có cực đa ̣i và không có cực tiểu
D) Hàm số không có cực tri ̣
Câu 11. Tı̀m tất cả các giá tri ̣ của tham số m để hàm số y  x4  ( 2 m  )
1 x2  m có ba cực tri ̣.
A) m  2
B) m  1
C) m  0
D) m  1
Câu 12. Cho hàm số y  f (x) xác đi ̣nh, liên tu ̣c trên tâ ̣p R và có bảng biến thiên như hı̀nh vẽ sau.
Trong các khẳng đi ̣nh sau, khẳng đi ̣nh sai là:
A) Hàm số đa ̣t cực đa ̣i ta ̣i x  2
B) Hàm số đồng biến trên khoảng ( ; 2); (0; )
C) Đồ thi ̣ hàm số không có đường tiê ̣m câ ̣n
D) Giá tri ̣ nhỏ nhất của hàm số bằng  1
Câu 13. Với giá trị nào của tham số m thì đồ thị hàm số 4
y  x  ( 2 m  ) 1 2 4
x  m  3 2
m  2017 có ba
điểm cực trị tạo thành một tam giác có diện tích bằng 32 ?
A) m  2
B) m  3
C) m  4
D) m  5
Câu 14. Đồ thị hàm số nào sau đây có đường tiệm cận ngang là y  2 1 2 1  2 2 A) x x x
y  2  B) y  C) y  D) y  x x  2 x  3 2 x  2 Trang 1/3 2 2   1
Câu 15. Đồ thi ̣ ha x x ̀m số y 
có ba đường tiê ̣m câ ̣n thı̀ tâ ̣p giá tri ̣ của tham số thực m là:
x 2  m 2  m A) (0; ) 1 B) (0; )
C) ( ;0)  1 ( ; ) D) ( ; ) 1
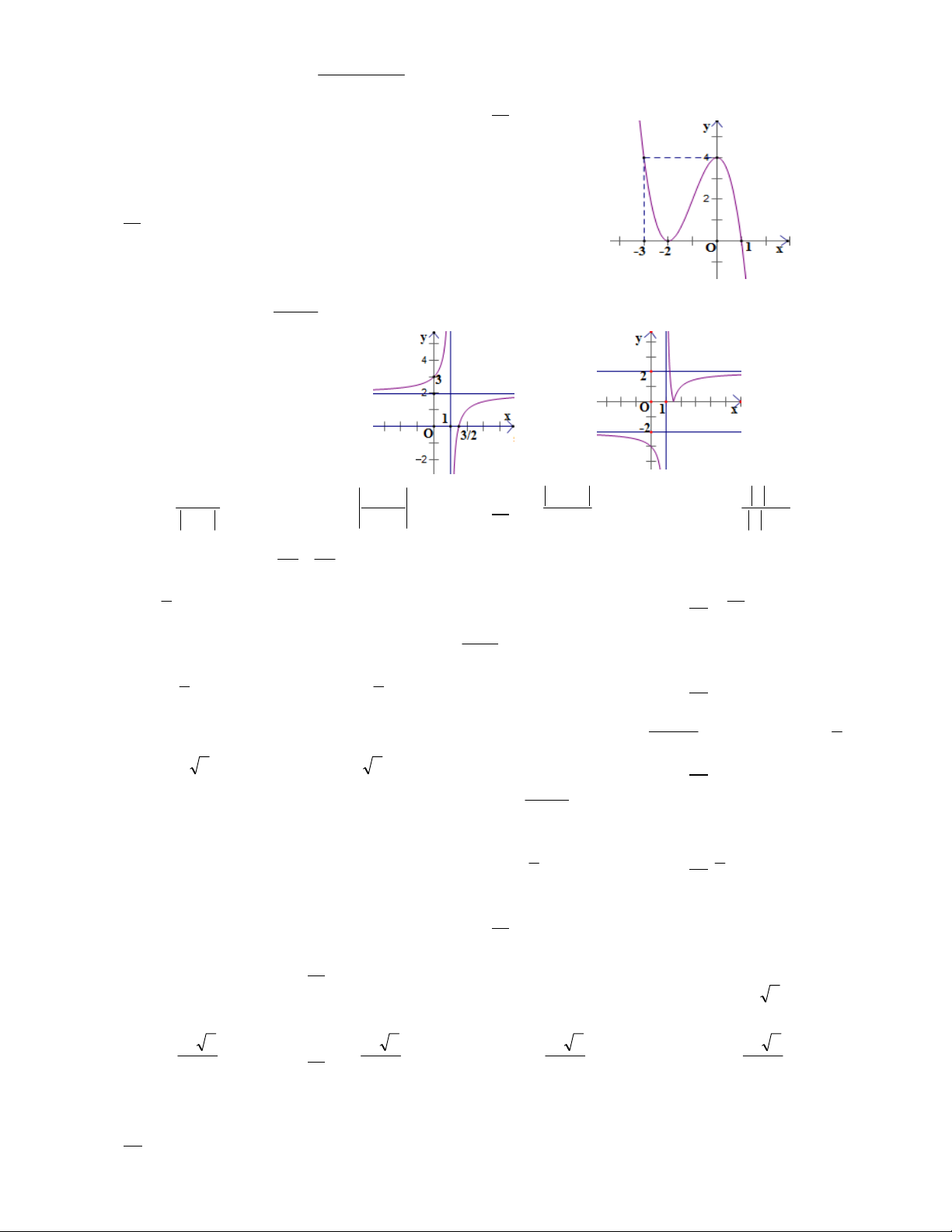
Câu 16. Cho hàm số y  f (x) có đồ thi ̣ như hı̀nh bên.
Trong các mê ̣nh đề sau, mê ̣nh đề sai là:
A) Hàm số đa ̣t cực tiểu ta ̣i x  2
B) Hàm số đồng biến trên khoảng (2;4)
C) Hàm số có hai cực tri ̣
D) Đồ thi ̣ hàm số và tru ̣c Ox có hai điểm chung 2x  3
Câu 17. Hàm số y 
có đồ thi ̣ là (H1). Hỏi (H2) là đồ thi ̣ của hàm số nào trong bốn hàm số sau ? x  1 (H1) (H2) 2x  3 2x  3 2x  3 2 x  3 A) y  B) y  C) y  D) y  x  1 x  1 x  1 x  1 3 2
Câu 18. Hàm số  x y
 x  2x  1 có giá tri ̣ nhỏ nhất trên đoạn 0;2 bằng: 3 2 1 13 A)  B) 0 C)  1 D)  3 6 1
Câu 19. Giá tri ̣ nhỏ nhất m của hàm số y  x 
trên  1;2 là: x  2 9 1 A) m  B) m  
C) m  2
D) m  0 4 2 2 x  1 Câu 20. Tı m
̀m các giá tri ̣ của tham số m để giá tri ̣ nhỏ nhất của hàm số y 
trên 0;2 bằng  x  2 2
A) m   3
B) m  3
C) m  1
D) m  1 7 x  6
Câu 21. Gọi M và N là giao điểm của đường cong y 
và đường thẳng y  x  2 . Khi đó hoành x  2
độ trung điểm I của đoạn MN bằng: 7 7 A) 7 B) 3 C)  D) 2 2
Câu 22. Số giao điểm của hai đồ thị 3 2
y  x  x  2x  3; 2
y  x  x  1 là A) 0 B) 1 C) 3 D) 2
Câu 23. Đồ thi ̣ hàm số y  x3  3x2  m cắt tru ̣c Ox ta ̣i ba điểm phân biê ̣t thı̀ tâ ̣p giá tri ̣ của m là:
A) (; 4)  (0; ) B) (4;0) C) (0; 4) D) (0; )
Câu 24. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B , AB  a, BC  a 2 . SA vuông
góc với đáy, SA  a
2 . Tính theo a thể tích V của khối chóp S.ABC . 3 a 2 3 a 2 3 a 2 3 a 3 A) V  B) V  C) V  D) V  2 3 6 6
Câu 25. Cho hình chóp S.ABC đáy là tam giác vuông tại B , cạnh bên SA  ( ABC) . Biết SA  a 3 ,
AB  a
2 , BC  a . Thể tích V của khối chóp S.ABC là: A) 3
V  a B) 3
V  2a C) 3
V  3a D) 3
V  4a Trang 2/3
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy và SA  a 3 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 A) 3 V  3a B) 3 V  a C) 3 V  a D) 3 V  a 6 3 9
Câu 27. Khối chóp có diê ̣n tı́ch đáy là B và chiều cao là h thı̀ thể tı́ch V của khối chóp đó là: A) 1 V 
B.h
B) V  B h .
C) V  3B h . D) 2
V  B.h 3
Câu 28. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a
2 . Góc giữa mặt bên và mặt đáy bằng 0
60 .Tính theo a thể tích khối chóp S.ABCD . 4 3 a 3 3 a 3 4 3 a 2 4 3 a 6 A) V  B) V  C) V  D) V  3 3 3 3
Câu 29. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , hai mặt phẳng (SAB) và (SAD) cùng
vuông góc với đáy, cạnh bên SC tạo với đáy góc 0
60 . Thể tích khối chóp đã cho bằng : 3 4 3 a 6 a 6 2 3 a 6 4 3 a 2 A) V  B) V  C) V  D) V  3 3 3 3
Câu 30. Cho hình chóp tứ giác đều (H) có diện tích đáy bằng 4 và diện tích của một mặt bên bằng 2 .
Thể tích V của (H) là: 4 3 4 4 2 A) V 
B) V  4 C) V  D) V  3 3 3
Câu 31. Cho hình chóp S.ABCD có đáy là hình vuông có cạnh a . Mặt bên SAB là tam giác đều nằm
trong mặt phẳng vuông góc với đáy (ABCD) . Tính thể tích V khối chóp S.ABCD 3 a 3 3 a 3 3 a 3 A) V  B) 3
V  a 3 C) V  D) V  6 2 3
Câu 32. Cho một tứ diện đều có chiều cao h . Ở ba góc của tứ diện
người ta cắt đi các tứ diện đều bằng nhau có chiều cao x để khối
đa diện còn lại có thể tích bằng một nửa thể tích tứ diện đều ban
đầu (hình bên ). Giá trị của x là bao nhiêu? A) h h x  B) x  3 2 3 3 C) h h x  D) x  3 4 3 6
Câu 33. Cho hı̀nh chóp S.ABC có đáy ABC là tam đều ca ̣nh a , SA  (ABC) . Góc giữa SB và đáy bằng 0
60 . Khoảng cách d giữa AC và SB là: 2 15 7
A) d  a 2 B) d  a C) d  a D) d  a 2 5 7
********* Hết ********* Trang 3/3