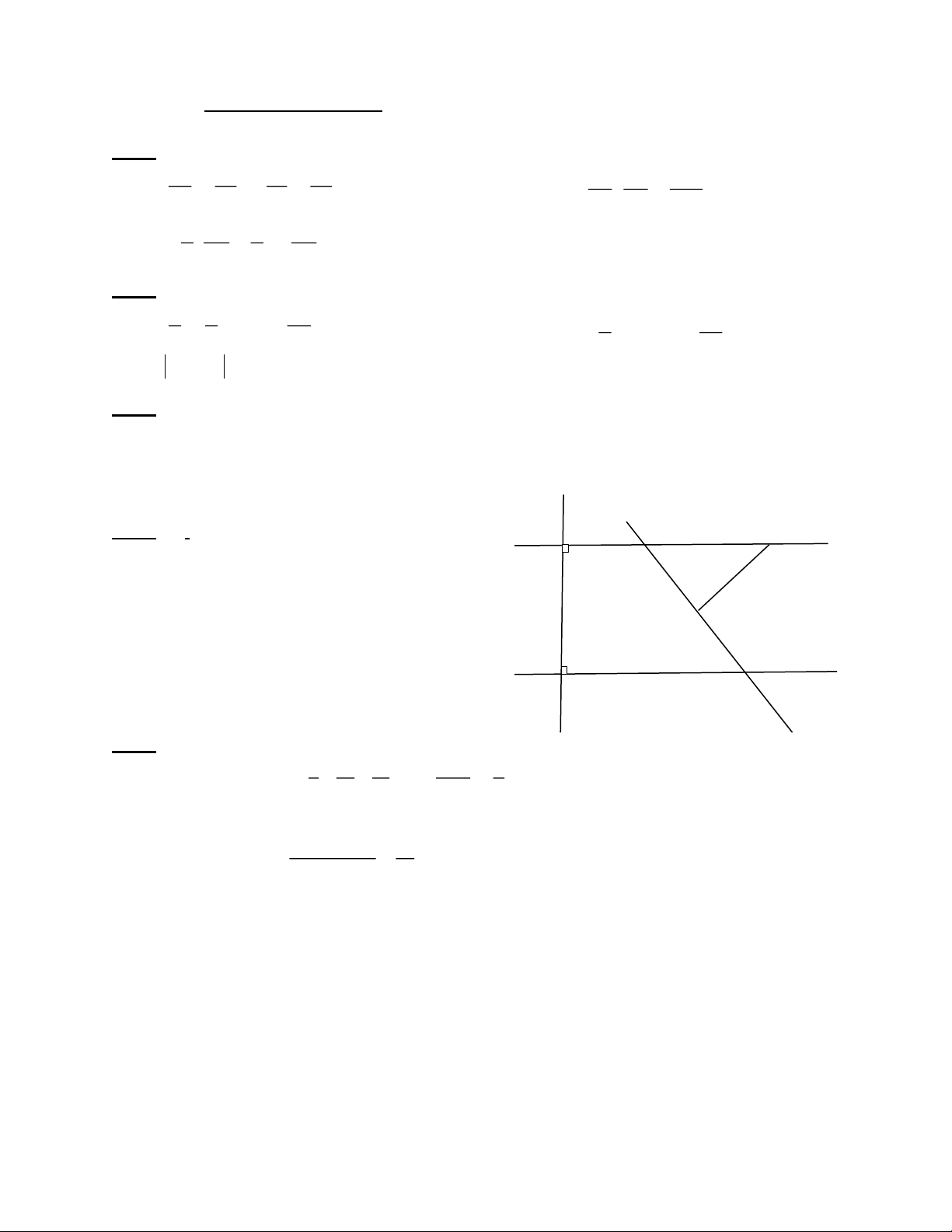

Preview text:
TRƯỜNG TH&THCS THỤY CHÍNH
ĐỀ KIỂM TRA GIỮA KÌ I
NĂM HỌC: 2021 - 2022 Môn: Toán 7
(Thời gian làm bài 90 phút)
Bài 1:(2,0 điểm) Tính hợp lý : 5 − 4 17 43 − − a) + + − 5 12 21 c) . . 12 39 12 39 6 7 − 15 3 −8 3 −3 b) . − : d) ( )100 102 0,125 .8 5 3 5 2
Bài 2:(2,5 điểm) Tìm x biết : 3 1 2 − 2 a) + : x = 2 9 c) − = 4 4 5 3x 5 25 b) x + 0,8 − 12,9 = 0 d) x x+2 3 + 3 = 810 Bài 3:(1,5 điểm)
Trong đợt thi đua giành hoa diểm tốt chào mừng ngày nhà giáo Việt Nam, số điểm tốt (từ 9
điểm trở lên) của ba lớp7A, 7B, 7C lần lượt tỉ lệ với 13; 15 và 21 . Biết số điểm tốt của hai lớp
7A và 7B nhiều hơn số điểm tốt của lớp 7C là 63 điểm. Tính số điểm tốt của mỗi lớp
Bài 4:(3, 0 điểm) Cho hình vẽ A E F
Hãy vẽ lại hình và chú thích đầy đủ a : Biết: a ⊥ c, b ⊥ c, FDC ̂ = 1100, bCy ̂ = 550 a) Chứng minh a//b 1100
b) Tính các góc của ∆DEF. D
c) Kẻ Tia Dn là tia phân giác của FDC ̂ B Chứng minh Dn//a b 550 C c y Bài 5: (1 điểm) 1 1 1 1 1 a) Chứng minh A = + + +...+ . 2 3 2020 3 3 3 3 2
b) Cho 4 số a , a , a , a khác 0 và thỏa mãn: 2
a = a .a và 2
a = a .a 1 2 3 4 2 1 3 3 2 4 3 3 3 a + a + a a Chứng minh rằng: 1 2 3 1 = 3 3 3 a + a + a a 2 3 4 4
HƯỚNG DẪN CHẤM TOÁN 7- ĐỀ CHẴN
ĐỀ KIỂM TRA GIỮA KỲ I
NĂM HỌC 2021 – 2022 Bài Câu Nội dung Điểm 14 29 71 6 − 14 71 29 6 − + − + = − + + a) 57 23 57 23
57 57 23 23 0.5 1 0,5đ = ( 1 − )+1= 0 (2,0đ) b) 5 3 − 7 3 − 3 − 5 7 3 − 0.5 0.5đ + = + = . . 12 4 12 4 4 12 12 4 c) 3 − 5 1 − 5 26 3 − 22 1 − 5 3 3.11.2.15.3 9 0.5 0.5đ = = = : . : . . . 11 22 3 3 11 5 3 26 11.5.3.2.13 13 d) ( )100 103 0, 25 .4 = ( )100 100 3 100 3 0, 25
.4 .4 = (0, 25.4) .4 = 1.64 = 64 0.5 0.5đ 3 − 2 − 1 + : x = 5 5 3 2 − 1 3 − : x = − 5 3 5 0.25 a) 2 − 14 : x = 0.75đ 5 15 −2 14 0.25 = x : 5 15 3 = − x 7 2 3 0.25 Vây x = − 7 + − = (2.5đ) b) 0, 2 x 1,3 1,5 − = 0.5đ x 1,3 1,3 x −1,3 = 1,3 0,25 x 0; 2, 6 Vây x 0; 2, 6 0.25 c) 2 3 4 − 2x = 0.75đ 7 9 2 2 3 2 − 2x = 7 3 0,25 3 2 − 2x = 7 3 5 − 23 x ; 42 42 5 − 23 0.5 Vây x ; 42 42 x x+3 2 + 2 = 144 d) x 3 2 (1 + 2 ) = 144 0.25 0.5đ x 2 = 16 x = 4 0.25 Vậy x = 4
Gọi số học sinh của ba khối 6, 7 , 8 lần lượt là : x, y , z *
(x, y, z N )
Ví số học sinh của ba khối tỉ lệ với 41; 30; 29 nên: x y z = = 0.5 3 41 30 29
(1.5đ) 1.5đ Mà tổng số học sinh của khối 6 và khối 8 hơn khối 7 là 320 em nên: x + z – y = 320. 0.25
Áp dụng tính chất dãy tỉ số bằng nhau ta được: x y z
x + z − y 320 = = = = = 0.25 8 41 30 29 41+ 29 − 30 40 x = 328
y = 240 ( thỏa mãn điều kiện) 0.25 z = 232
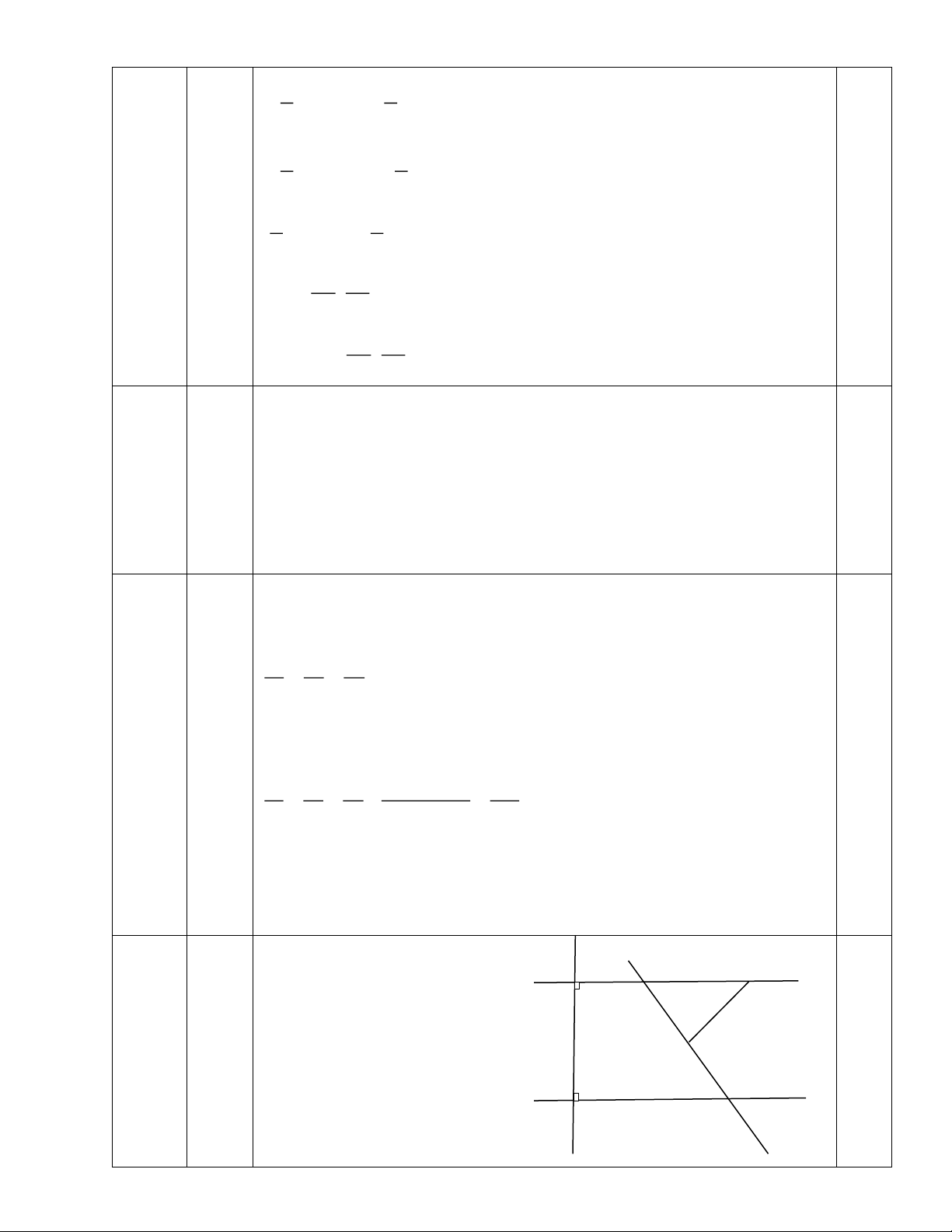
Vậy số học sinh khối 6, 7,8 lần lượt là 328, 240 và 232 em. 0.25 E Vẽ hình, ghi GT, KL A F a D 1100 0.5 0.5đ B b 55 4 C 0 c y a) a ⊥ c, b ⊥ c => a//b (3,0đ) 0.75 0.75đ 0.25 Do a // b => yCb ̂ = ⋯ = FED ̂ = 550 b) ∆DEF 0,5 => .... 0.75đ 0.5 =>....
Ta có :Dn là tia phân giác FDC ̂ =>.... c) =>……. 0.25 0.5đ => DN//b//c 0.25 1 1 1 1 1 A = + + + ...+ + 2 3 2019 2020 4 4 4 4 4 a) 1 1 1 1 = + + + + + 0.5đ 4 A 1 ... 2 3 2019 4 4 4 4 0.25 1 5
4A− A= 1− 2020 4 1 3A = 1− 2020 4 (1,0đ) 1 1 1 A = − 0.25 2020 3 3.4 3 a b 2 b = . a c = Từ b c b c 2 c = . b d = c d b) a b c = = 0.5đ b c d 0.25 3 3 3 a b c = = b c d 3 3 3 a b c = = . 3 3 3 b c d
Áp dụng tính chất dãy tỉ số bằng nhau ta được: 3 3 3 3 3 3 a b c a + b + c a b c a = = = = . . = ( đpcm) 3 3 3 3 3 3 0.25 b c d b + c + d b c d d
Chú ý: Học sinh có cách giải khác đúng thì cho điểm tương đương.
Bài hình học sinh không vẽ lại hoặc vẽ sai hình thì không chấm điểm.




