Đề thi giữa kỳ 2 Toán 10 năm 2023 – 2024 trường THPT Quế Sơn – Quảng Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra giữa học kỳ 2 môn Toán 10 năm học 2023 – 2024 trường THPT Quế Sơn, tỉnh Quảng Nam; đề thi có đáp án và hướng dẫn chấm điểm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Thông tin:

11 trang 5 tháng trước

Tác giả:

Profile M. Hậu
Trang 1/4 - Mã đề 101
ĐỀ CHÍNH THỨC
TRƯỜNG THPT QUẾ SƠN
TỔ:TOÁN - TIN
(Đề gồm có 04 trang)
KIỂM TRA GIỮA KỲ 2- NĂM HỌC 2023-2024
Môn: TOÁN – Lớp 10
Thời gian: 90 phút (Không kể thời gian giao đề)
MÃ ĐỀ 101
A. TRẮC NGHIỆM ( 35 câu x 0,2 = 7,0 điểm).
Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.
Câu 1. Cho biểu đồ nhiệt độ cao nhất trong ngày vào tuần cuối của tháng 3 năm 2024 tại thành phố Tam
Kỳ, tỉnh Quảng Nam. Biểu đồ cho ta một hàm số. Từ biểu đồ, thì nhiệt độ cao nhất vào ngày Thứ 5 là:
24
25
26
27
28
29
30
31
32
33
Thứ 2 Thứ 3 Thứ 4 Thứ 5 Thứ 6 Thứ 7 Chủ nhật
o
C
Biểu đồ nhiệt độ
(Theo https://www.accuweather.com/vi/vn/tam-ky/355712/january-weather).
A.
0
29 C
. B.
0
30 C
. C.
0
31 C
. D.
0
32 C
.
Câu 2. Xét hai đại lượng
phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì
y
không
phải là một hàm số của
?x
A.
2
24xy
. B.
4
y
x
. C.
2
4xy
. D.
24xy
.
Câu 3. Cho hàm số
()y f x
có bảng giá trị sau:
x
…
2
1
0
1
2
…
()fx
…
4
2
0
2
4
…
Hàm số
()y f x
là hàm số nào sau đây?
A.
2
yx
. B.
2
yx
. C.
2yx
. D.
2yx
.
Câu 4. Một hiệu cho thuê xe máy niêm yết giá như sau: giá thuê xe là 100 nghìn đồng cho mỗi ngày trong 2
ngày đầu tiên và 80 nghìn đồng cho mỗi ngày tiếp theo. Gọi T(x) là tổng số tiền phải trả (nghìn đồng) theo
số ngày x mà khách thuê xe. Công thức của T(x) thu được là:
A.
100 0 2
()
80 2 2
x khi x
Tx
x khi x


. B.
100 0 2
()
200 80 2 2
x khi x
Tx
x khi x

.
C.
100 0 2
()
200 80 2
x khi x
Tx
x khi x


. D.
100 0 2
()
80 2
x khi x
Tx
x khi x

.
Thứ
…
Trang 2/4 - Mã đề 101
Câu 5. Tập xác định
D
của hàm số
2
x
y
x
là:
A.
\ 0;2D
. B.
\0D
. C.
\2D
. D.
0;2D
.
Câu 6. Phương trình trục đối xứng của Parabol
2
: 2 1P y x x
là:
A.
1.x
B.
2.x 
C.
1.x 
D.
2.x
Câu 7. Cho parabol
2
: 3 2 1P y x x
. Điểm nào sau đây là đỉnh của
?
A.
12
;
33
K



. B.
12
;
33
J



. C.
0;1I
. D.
12
;
33
H



.
Câu 8. Cho hàm số bậc hai
2
0y ax bx c a
có đồ thị như hình vẽ sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
2; .
B.
;2 .
C.
1; .
D.
1;3 .
Câu 9. Đồ thị sau đây là đồ thị của hàm số bậc hai nào?
A.
2
2 3.y x x
B.
2
2 3.y x x
C.
2
2 3.y x x
D.
2
2 3.y x x
Câu 10. Cho hàm số bậc hai
2
4 3.y x x
Hãy thay dấu “?” lần lượt bằng các số thích hợp nào để hoàn
thành bảng giá trị sau:
x
0
1
2
3
y
?
?
?
?
A.
3; 2; 4; 1
. B.
3; 5; 6; 7
. C.
3; 6; 7; 6
. D.
3; 5; 1; 2
.
Câu 11. Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ. Đặt
2
4b ac
, tìm dấu của
a
và
.
A.
0a
,
0.
B.
0a
,
0
. C.
0a
,
0
. D.
0a
,
0
Câu 12. Trong các hàm số sau, hàm nào có đồ thị luôn nằm hoàn toàn phía trên trục hoành?
A.
2
34f x x x
. B.
2
32f x x x
. C.
2
34f x x x
. D.
2
44f x x x
.
Trang 3/4 - Mã đề 101
Câu 13. Cho tam thức bậc hai
2
45f x x x
. Tìm tất cả giá trị của
x
để
0fx
.
A.
1;5x
. B.
; 1 5;x
. C.
5;1x
. D.
5;1x
.
Câu 14. Cho tam thức
2
6x 2024f x x
. Khẳng định nào sau đây là đúng?
A.
0fx
khi
3x
. B.
0fx
khi
3x
.
C.
0fx
với mọi
x
. D.
0fx
khi
3x
.
Câu 15. Cho tam thức bậc hai
2
56f x x x
. Mệnh đề nào sau đây đúng?
A.
0 2;3f x x
. B.
0 ;2 3;f x x 
.
C.
0 2;3f x x
. D.
( ) 0 2;3f x x
.
Câu 16. Tìm tất cả các giá trị của tham số
m
để phương trình
2
20x x m
có 2 nghiệm phân biệt.
A.
4.m
B.
1.m
C.
1.m
D.
4.m
Câu 17. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng
: 3 2024 0d x y
?
A.
(1;3).n
B.
( 3; 1).n
C.
(6;2).n
D.
(6; 2).n 
Câu 18. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
23
:
xt
yt

?
A.
( 3;0).u 
B.
(3;1).u
C.
(6; 2).u 
D.
( 1;3).u 
Câu 19. Điểm nào sau đây thuộc đường thẳng
: 3 9 0d x y
A.
(3;0).M
B.
( 3; 1).N 
C.
(6;2).P
D.
(0;9).Q
Câu 20. Vị trí tương đối của hai đường thẳng
1
3
:
12
xt
yt

và
2
1
:
32
xs
ys


,
là các tham số) là:
A. Trùng nhau. B. Cắt nhau nhưng không vuông góc nhau.
C. Song song. D. Vuông góc nhau.
Câu 21. Đường thẳng
:3 2 7 0xy
song song với đường thẳng nào sau đây?
A.
1
:6 4 14 0d x y
. B.
2
: 3 2 7 0d x y
. C.
3
:3 2 0d x y
. D.
4
:3 2 0d x y
.
Câu 22. Đường thẳng
:3 2 7 0xy
cắt đường thẳng nào sau đây?
A.
1
:6 4 14 0d x y
. B.
2
: 3 2 7 0d x y
. C.
3
:3 2 0d x y
. D.
4
:3 2 0d x y
.
Câu 23. Đường thẳng
:2 4 1 0d x y
vuông góc với đường thẳng nào sau đây?
A.
1
:2 14 0d x y
. B.
2
: 2 7 0d x y
. C.
3
:2 7 0d x y
. D.
4
:3 5 0d x y
.
Câu 24. Tìm m để 2 đường thẳng
1
:2 1 0.xy
và
2
:4 7 0x my
vuông góc với nhau?
A.
2.m
B.
2.m 
C.
8.m 
D.
8.m
Câu 25. Phương trình nào sau đây không phải là phương trình tổng quát một đường thẳng?
A.
3 2 3 0xy
. B.
2 3 0y 
. C.
3 1 0x
. D.
2
3 5 0xy
.
Câu 26. Phương trình tổng quát đường thẳng
d
đi qua điểm
(1;2)M
và có 1 vectơ pháp tuyến
2;3n
là:
A.
2 3 8 0xy
. B.
2 3 8 0xy
. C.
4 6 1 0xy
. D.
2 3 12 0xy
.
Câu 27. Cho hai đường thẳng
1
22
:
54
xt
d
yt


và
2
1
:
13
xs
d
ys


,
là các tham số). Góc giữa hai
đường thẳng
1
d
và
2
d
là:
A.
90
. B.
45
. C.
60
. D.
30
.
Trang 4/4 - Mã đề 101
Câu 28. Tìm tọa độ tâm
I
và bán kính
R
của đường tròn (C):
22
( 1) ( 3) 8xy
A.
( 1;3), 8.IR
B.
(1; 3), 8.IR
C.
( 1;3), 2 2.IR
D.
(1; 3), 2 2.IR
Câu 29. Tìm tọa độ tâm
I
và bán kính
R
của đường tròn (C:
22
8 4 5 0x y x y
.
A.
(4; 2), 2 5.IR
B.
(4; 2), 5.IR
C.
( 4;2), 5.IR
D.
( 4;2), 2 5.IR
Câu 30. Đường tròn
()C
có tâm
(2;3)I
và qua điểm M(2; 0) có phương trình là:
A.
22
( 2) ( 3) 9xy
B.
22
( 2) ( 3) 13xy
C.
22
( 2) ( 3) 13xy
D.
22
( 2) ( 3) 9xy
Câu 31. Phương trình nào sau đây là phương trình chính tắc của đường elip?
A.
22
1
9 16
xy

. B.
22
1
16 9
xy

. C.
22
1
16 9
xy

. D.
22
0
25 16
xy

.
Câu 32. Phương trình nào sau đây là phương trình chính tắc của đường hypebol?
A.
22
1
34
xy

. B.
22
1
96
xy

. C.
22
0
25 16
xy

. D.
22
1
16 9
yx

.
Câu 33. Cho elip (E) có phương trình chính tắc
22
1
25 16
xy
. Tiêu cự của (E) bằng:
A. 3. B. 6. C. 8. D. 10.
Câu 34. Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A.
2
4yx
. B.
2
8yx
. C.
2
4yx
. D.
4yx
.
Câu 35. Parabol nào sau đây có tham số tiêu bằng 4?
A.
2
4yx
. B.
2
8yx
. C.
2
2yx
. D.
2
16yx
.
B. TỰ LUẬN ( 3,0 điểm).
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ
Oxy
, cho 2 điểm
(5; 4)M
,
(1; 1)N
. Viết phương trình tổng
quát đường thẳng
qua 2 điểm M, N.
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ
Oxy
, cho điểm
(3; 4)A
và đường thẳng d:
4 3 2024 0xy
.
Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
Câu 3 (0,5 điểm). Giải phương trình
2
2 5 3 1x x x
.
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 500 người. Với giá vé 50 000 đồng mỗi vé, trung bình
sẽ có khoảng 200 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến rạp mỗi
ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
------------------------ HẾT ------------------------
Trang 1/4 - Mã đề 102
ĐỀ CHÍNH THỨC
TRƯỜNG THPT QUẾ SƠN
TỔ:TOÁN - TIN
(Đề gồm có 04 trang)
KIỂM TRA GIỮA KỲ 2- NĂM HỌC 2023-2024
Môn: TOÁN – Lớp 10
Thời gian: 90 phút (Không kể thời gian giao đề)
MÃ ĐỀ 102
A. TRẮC NGHIỆM ( 35 câu x 0,2 = 7,0 điểm).
Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.
Câu 1. Cho biểu đồ nhiệt độ cao nhất trong ngày vào tuần cuối của tháng 3 năm 2024 tại thành phố Tam
Kỳ, tỉnh Quảng Nam. Biểu đồ cho ta một hàm số. Từ biểu đồ, thì nhiệt độ cao nhất vào ngày Thứ 6 là:
24
25
26
27
28
29
30
31
32
33
Thứ 2 Thứ 3 Thứ 4 Thứ 5 Thứ 6 Thứ 7 Chủ nhật
o
C
Biểu đồ nhiệt độ
(Theo https://www.accuweather.com/vi/vn/tam-ky/355712/january-weather).
A.
0
29 C
. B.
0
30 C
. C.
0
31 C
. D.
0
32 C
.
Câu 2. Xét hai đại lượng
phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì
y
không
phải là một hàm số của
?x
A.
2
4xy
. B.
4
y
x
. C.
24xy
. D.
2
24xy
.
Câu 3. Cho hàm số
()y f x
có bảng giá trị sau:
x
…
2
1
0
1
2
…
()fx
…
4
2
0
2
4
…
Hàm số
()y f x
là hàm số nào sau đây?
A.
2
yx
. B.
2
yx
. C.
2yx
. D.
2yx
.
Câu 4. Một hiệu cho thuê xe máy niêm yết giá như sau: giá thuê xe là 100 nghìn đồng cho mỗi ngày trong 3
ngày đầu tiên và 60 nghìn đồng cho mỗi ngày tiếp theo. Gọi T(x) là tổng số tiền phải trả (nghìn đồng) theo
số ngày x mà khách thuê xe. Công thức của T thu được là:
A.
100 0 3
()
60 3 3
x khi x
Tx
x khi x


. B.
100 0 3
()
60 3
x khi x
Tx
x khi x

.
C.
100 0 3
()
300 60 3
x khi x
Tx
x khi x


. D.
100 0 3
()
300 60 3 3
x khi x
Tx
x khi x

.
Thứ
…
Trang 2/4 - Mã đề 102
Câu 5. Tập xác định
D
của hàm số
1
3
x
y
x
là:
A.
\ 1;3D
. B.
\3D
. C.
\1D
. D.
1;3D 
.
Câu 6. Phương trình trục đối xứng của Parabol
2
23y x x
là:
A.
1.x
B.
2.x 
C.
1.x 
D.
2.x
Câu 7. Cho parabol
2
: 3 2 1P y x x
. Điểm nào sau đây là đỉnh của
?
A.
0;1I
. B.
12
;
33
J



. C.
12
;
33
K



. D.
12
;
33
H



.
Câu 8. Cho hàm số bậc hai
2
0y ax bx c a
có đồ thị như hình vẽ sau:
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
1; .
B.
;1 .
C.
4; . 
D.
1;3 .
Câu 9. Đồ thị sau đây là đồ thị của hàm số bậc hai nào?
A.
2
4 3.y x x
B.
2
4 3.y x x
C.
2
2 3.y x x
D.
2
2 3.y x x
Câu 10. Cho hàm số bậc hai
2
4 5.y x x
Hãy thay dấu “?” lần lượt bằng các số thích hợp nào để hoàn
thành bảng giá trị sau:
x
0
1
2
3
y
?
?
?
?
A.
5; 2; 4; 1
. B.
5; 2; 1; 7
. C.
5; 2; 4; 7
. D.
5; 2; 1; 2
.
Câu 11. Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ. Đặt
2
4b ac
, tìm dấu của
a
và
.
x
y
O
A.
0a
,
0.
B.
0a
,
0
. C.
0a
,
0
. D.
0a
,
0
Câu 12. Trong các hàm số sau, hàm nào có đồ thị luôn nằm hoàn toàn phía dưới trục hoành?
A.
2
34f x x x
. B.
2
32f x x x
. C.
2
34f x x x
. D.
2
45f x x x
.
Trang 3/4 - Mã đề 102
Câu 13. Cho tam thức bậc hai
2
45f x x x
. Tìm tất cả giá trị của
x
để
0fx
.
A.
1;5x
. B.
; 5 1;x 
. C.
5;1x
. D.
5;1x
.
Câu 14. Cho tam thức
2
6x 2024f x x
. Khẳng định nào sau đây là đúng?
A.
0fx
khi
3x
. B.
0fx
khi
3x
.
C.
0fx
khi
3x
. D.
0fx
với mọi
x
.
Câu 15. Cho tam thức bậc hai
2
56f x x x
. Mệnh đề nào sau đây sai?
A.
0 2;3f x x
. B.
0 ;2 3;f x x 
.
C.
0 2;3f x x
. D.
( ) 0 2;3f x x
.
Câu 16. Tìm tất cả các giá trị của tham số
m
để phương trình
2
20x x m
vô nghiệm.
A.
4.m
B.
1.m
C.
1.m
D.
4.m
Câu 17. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng
:3 2024 0d x y
?
A.
( 1;3).n 
B.
( 3; 1).n
C.
( 3;1).n 
D.
(6; 2).n 
Câu 18. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
23
:
xt
yt

?
A.
( 3;0).u 
B.
( 3; 1).u
C.
(6;2).u
D.
( 3;1).u 
Câu 19. Điểm nào sau đây thuộc đường thẳng
: 3 9 0d x y
A.
(3;0).M
B.
( 3; 1).N 
C.
(6;2).P
D.
(0;9).Q
Câu 20. Vị trí tương đối của hai đường thẳng
1
2
:
12
xt
yt


và
2
1
:
32
xs
ys


,
là các tham số) là:
A. Vuông góc nhau. B. Cắt nhau nhưng không vuông góc nhau.
C. Song song. D. Trùng nhau.
Câu 21. Đường thẳng
:3 2 7 0xy
song song với đường thẳng nào sau đây?
A.
1
:6 4 14 0d x y
. B.
2
:3 2 0d x y
. C.
3
: 3 2 7 0d x y
. D.
4
:3 2 0d x y
.
Câu 22. Đường thẳng
:3 2 7 0xy
cắt đường thẳng nào sau đây?
A.
1
:3 2 0d x y
. B.
2
: 3 2 7 0d x y
. C.
3
:3 2 0d x y
. D.
4
:6 4 14 0d x y
.
Câu 23. Đường thẳng
:2 4 1 0d x y
vuông góc với đường thẳng nào sau đây?
A.
1
:2 14 0d x y
. B.
2
:2 10 0d x y
. C.
3
:2 7 0d x y
. D.
4
:3 5 0d x y
.
Câu 24. Tìm m để 2 đường thẳng
1
:2 1 0.xy
và
2
:4 7 0x my
vuông góc với nhau?
A.
2.m
B.
2.m 
C.
8.m 
D.
8.m
Câu 25. Phương trình nào sau đây không phải là phương trình tổng quát một đường thẳng?
A.
2
3 2 3 0xy
. B.
2 3 0y 
. C.
3 1 0x
. D.
2 5 0xy
.
Câu 26. Phương trình tổng quát đường thẳng
d
đi qua điểm
(1;2)M
và có 1 vectơ pháp tuyến
2;3n 
là:
A.
2 3 8 0xy
. B.
2 3 4 0xy
. C.
2 3 1 0xy
. D.
2 3 12 0xy
.
Câu 27. Cho hai đường thẳng
1
2
:
52
xt
d
yt


và
2
1
:
13
xs
d
ys


,
là các tham số). Góc giữa hai
đường thẳng
1
d
và
2
d
là:
A.
90
. B.
60
. C.
45
. D.
30
.
Trang 4/4 - Mã đề 102
Câu 28. Tìm tọa độ tâm
I
và bán kính
R
của đường tròn (C):
22
( 1) ( 3) 8xy
A.
( 1;3), 8.IR
B.
(1; 3), 8.IR
C.
( 1;3), 2 2.IR
D.
(1; 3), 2 2.IR
Câu 29. Tìm tọa độ tâm
I
và bán kính
R
của đường tròn (C:
22
8 4 5 0x y x y
.
A.
(4; 2), 2 5.IR
B.
(4; 2), 5.IR
C.
( 4;2), 5.IR
D.
( 4;2), 2 5.IR
Câu 30. Đường tròn
()C
có tâm
( 2; 3)I 
và qua điểm M(
2
; 0) có phương trình là:
A.
22
( 2) ( 3) 9xy
B.
22
( 2) ( 3) 13xy
C.
22
( 2) ( 3) 13xy
D.
22
( 2) ( 3) 9xy
Câu 31. Phương trình nào sau đây là phương trình chính tắc của đường elip?
A.
22
1
96
xy

. B.
22
1
16 9
xy

. C.
22
1
69
xy

. D.
22
0
25 16
xy

.
Câu 32. Phương trình nào sau đây là phương trình chính tắc của đường hypebol?
A.
22
0
34
xy

. B.
22
1
96
xy

. C.
22
1
56
xy

. D.
22
1
16 9
yx

.
Câu 33. Cho elip (E) có phương trình chính tắc
22
1
25 9
xy
. Tiêu cự của (E) bằng:
A. 8. B. 6. C. 9. D. 10.
Câu 34. Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A.
4yx
. B.
2
8yx
. C.
2
4yx
. D.
2
4yx
.
Câu 35. Parabol nào sau đây có tham số tiêu bằng 2?
A.
2
4yx
. B.
2
8yx
. C.
2
2yx
. D.
2
16yx
.
B. TỰ LUẬN ( 3,0 điểm).
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ
Oxy
, cho 2 điểm
(2; 7)M
,
(5; 1)N
. Viết phương trình tổng
quát đường thẳng
qua 2 điểm M, N.
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ
Oxy
, cho điểm
( 4;3)A
và đường thẳng d:
3 4 2024 0xy
.
Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
Câu 3 (0,5 điểm). Giải phương trình
2
2 7 5 1x x x
.
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 400 người. Với giá vé 50 000 đồng mỗi vé, trung bình
sẽ có khoảng 160 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 40 người đến rạp mỗi
ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
------------------------ HẾT ------------------------
Đề\câu 101
102
103 104
1
A
C D
B
2
C D
A
A
3
D C D
C
4
B D D
B
5
C B
B D
6
C A D A
7
A B A
A
8
A A
C C
9
A B
B D
10
C D
D C
11
D
C B B
12
C A D A
13
C B A
B
14
C D
C
D
15
A A D C
16
B
C D D
17
D
B B D
18
B D C C
19
D A A A
20
A D B A
21
C B
C B
22
D A D C
23
C B C C
24
C D A
B
25
D A A D
26
A B A A
27
B
C A C
28
C D B A
29
B C C B
30
A D
B D
31
C A C B
32
A C D A
33
B A A B
34
C D C D
35
B A B
C
Đáp án Tự luận Toán 10_GK2_23-24
Trường THPT Quế Sơn
Tổ Toán-Tin
Hướng dẫn chấm Toán 10
GK2-2023-2024
Đề 101-103
Điểm
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ
Oxy
, cho 2 điểm
(5; 4)M
,
(1; 1)N
. Viết phương trình
tổng quát đường thẳng
qua 2 điểm M, N.
+ Đường thẳng
qua
(5; 4)M
và có VTCP
( 4;3)MN
+ Nên
có VTPT
(3;4)n
+ PTTQ
:
3( 5) 4( 4) 0xy
+
3 4 1 0xy
0,25
0,25
0,25
0,25
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ
Oxy
, cho điểm
(3; 4)A
và đường thẳng d:
4 3 2024 0xy
. Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
+ (C) có bán kính R =
22
4.3 3( 4) 2024
, 400
4 ( 3) .
d A d


+ (C) có tâm
(3; 4)A
và có bán kính R=400
Pt (C):
22
( 3) ( 4) 160000xy
0,25
0,25
Câu 3 (0,5 điểm). Giải phương trình
2
2 5 3 1x x x
.
+ Bình phương 2 vế phương trình đã cho ta được:
2
22
2 5 3 (1 )x x x
22
2 5 3 1 2x x x x
2
3 2 0xx
1
2
x
x
+ Thử lại ta thấy x = 1 là nghiệm của phương trình đã cho còn x = 2 không phải là nghiệm của
phương trình đã cho. Vậy phương trình đã cho có 1 nghiệm x = 1.
0,25
0,25
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 500 người. Với giá vé 50 000 đồng, trung bình sẽ
có khoảng 200 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến
rạp mỗi ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
+ Gọi x (nghìn đồng) là giá mỗi vé bán ra để doanh thu đạt lớn nhất
0 50x
.
Suy ra số tiền giảm giá mỗi vé so với mức giá cũ là:
50 x
(nghìn đồng)
+ Số người tăng lên khi giảm giá vé là:
50 50
5 50
10
x
x

+ Số người đến rạp chiếu phim mỗi ngày khi giảm giá vé là: 200 +
5 50 5 450xx
Doanh thu mỗi ngày khi giá vé x (nghìn đồng) là:
2
5 450T x x x
+ Ta có T(x) làm hàm số bậc 2 có đồ thị là parabol (P). T(x) đạt GTLN tại x
0
là hoành độ
đỉnh của (P) , khi đó x
0
= 45.
Vậy doanh thu lớn nhất trong ngày (là 10.125.000 đồng) khi giá mỗi vé là 45 000 đồng
0,25
0,25
0,25
0,25
Đáp án Tự luận Toán 10_GK2_23-24
Đề 102-104
Điểm
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ
Oxy
, cho 2 điểm
(2; 7)M
,
(5; 1)N
. Viết phương trình
tổng quát đường thẳng
qua 2 điểm M, N.
+
qua
(2; 7)M
và có 1 VTCP
(3;6)MN
+ Suy ra
có 1 VTPT
(2; 1)n
+ PTTQ
:
2( 2) 1.( 7) 0xy
+
2 11 0xy
0,25
0,25
0,25
0,25
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ
Oxy
, cho điểm
( 4;3)A
và đường thẳng d:
3 4 2024 0xy
. Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
+ (C) có bán kính R =
22
( 3).( 4) 4.3 2024
, 400
( 3) 4 .
d A d


+ (C) có tâm
( 4;3)A
và có bán kính R
400
Pt (C):
22
( 4) ( 3) 160000xy
0,25
0,25
Câu 3 (0,5 điểm). Giải phương trình
2
2 7 5 1x x x
.
+ Bình phương 2 vế phương trình đã cho ta được:
2
22
2 7 5 (1 )x x x
22
2 7 5 1 2x x x x
2
5 4 0xx
1
4
x
x
+ Thử lại ta thấy x = 1 là nghiệm của phương trình đã cho còn x = 4 không phải là nghiệm của
phương trình đã cho. Vậy phương trình đã cho có 1 nghiệm x = 1.
0,25
0,25
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 400 người. Với giá vé 50 000 đồng mỗi vé, trung
bình sẽ có khoảng 160 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim
đã khảo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 40
người đến rạp mỗi ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn
nhất.
+ Gọi x (nghìn đồng) là giá mỗi vé bán ra để doanh thu đạt lớn nhất
0 50x
.
Suy ra số tiền giảm giá mỗi vé so với mức giá cũ là:
50 x
(nghìn đồng)
+ Số người tăng lên khi giảm giá vé là:
40 50
4 50
10
x
x

+ Số người đến rạp chiếu phim mỗi ngày khi giảm giá vé là: 160 +
4 50 4 360xx
Doanh thu mỗi ngày khi giá vé x (nghìn đồng) là:
2
4 360T x x x
+ Ta có T(x) làm hàm số bậc 2 có đồ thị là parabol (P). T(x) đạt GTLN tại x
0
là hoành độ
đỉnh của (P), khi đó x
0
= 45.
Vậy doanh thu lớn nhất trong ngày (là 8.100. 000 đồng) khi giá mỗi vé là 45 000 đồng
0,25
0,25
0,25
0,25
Ghi chú: Học sinh giải theo cách khác mà đúng thì Thầy, Cô cho điểm tối đa theo thang điểm đã qui
định.
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT QUẾ SƠN
KIỂM TRA GIỮA KỲ 2- NĂM HỌC 2023-2024 TỔ:TOÁN - TIN
Môn: TOÁN – Lớp 10
Thời gian: 90 phút (Không kể thời gian giao đề) ĐỀ CHÍNH THỨC MÃ ĐỀ 101
(Đề gồm có 04 trang)
A. TRẮC NGHIỆM ( 35 câu x 0,2 = 7,0 điểm).
Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.
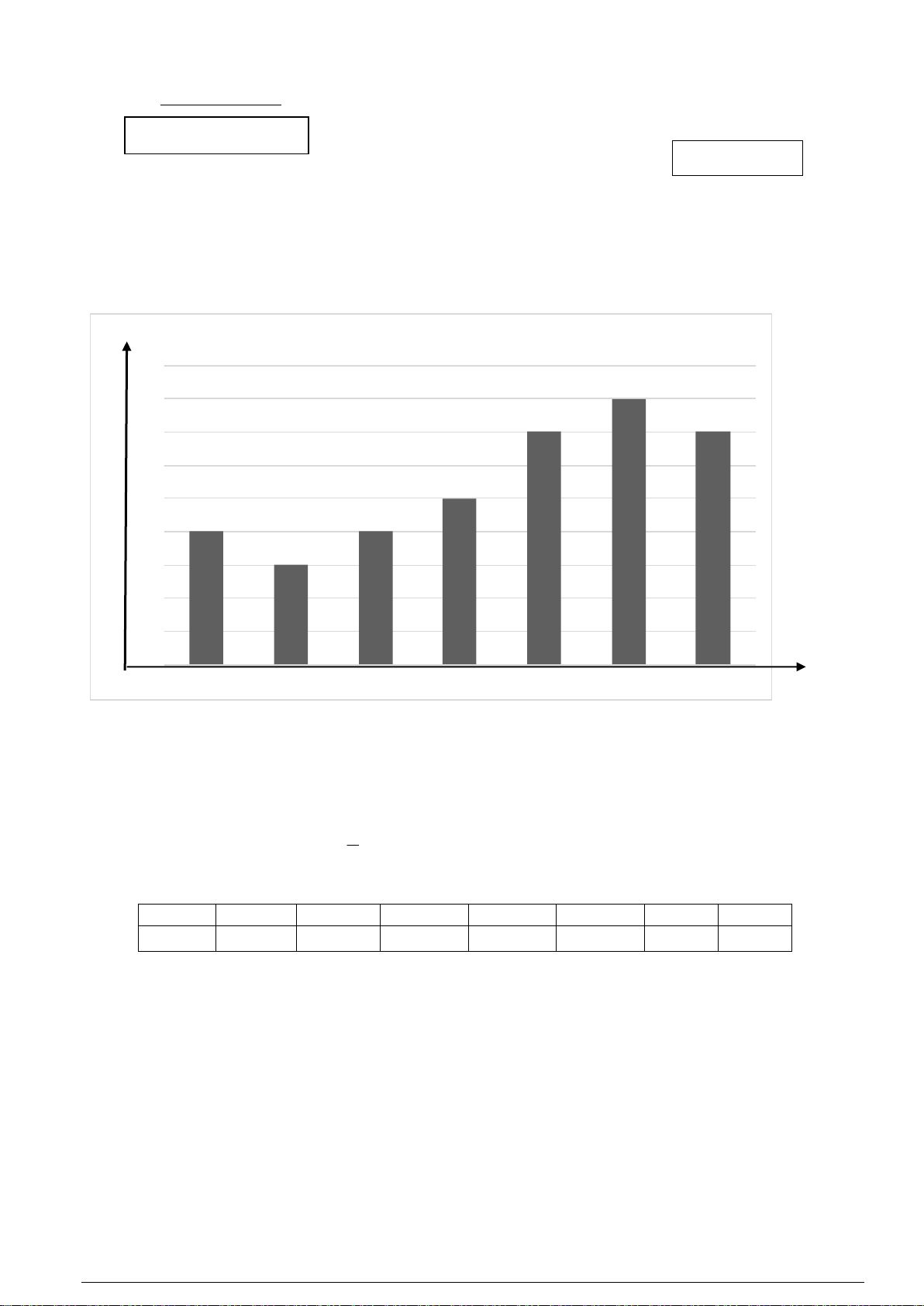
Câu 1. Cho biểu đồ nhiệt độ cao nhất trong ngày vào tuần cuối của tháng 3 năm 2024 tại thành phố Tam
Kỳ, tỉnh Quảng Nam. Biểu đồ cho ta một hàm số. Từ biểu đồ, thì nhiệt độ cao nhất vào ngày Thứ 5 là: oC
Biểu đồ nhiệt độ 33 32 31 30 29 28 27 26 25 … 24 Thứ 2 Thứ 3 Thứ 4 Thứ 5 Thứ 6 Thứ 7 Chủ nhậ t Thứ
(Theo https://www.accuweather.com/vi/vn/tam-ky/355712/january-weather). A. 0 29 C . B. 0 30 C . C. 0 31 C . D. 0 32 C .
Câu 2. Xét hai đại lượng ,
x y phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì y không
phải là một hàm số của x? 4 A. 2
x  2 y  4 . B. y  . C. 2 x y  4 .
D. 2x y  4 . x
Câu 3. Cho hàm số y f (x) có bảng giá trị sau: x … 2  1 0 1 2 … f (x) … 4 2 0 2  4  …
Hàm số y f (x) là hàm số nào sau đây? A. 2 y x . B. 2 y  x .
C. y  2x .
D. y  2x .
Câu 4. Một hiệu cho thuê xe máy niêm yết giá như sau: giá thuê xe là 100 nghìn đồng cho mỗi ngày trong 2
ngày đầu tiên và 80 nghìn đồng cho mỗi ngày tiếp theo. Gọi T(x) là tổng số tiền phải trả (nghìn đồng) theo
số ngày x mà khách thuê xe. Công thức của T(x) thu được là: 1  00x
khi 0  x  2  1  00x
khi 0  x  2 
A. T (x)  
. B. T (x)   . 8  0
  x  2 khi x  2 200  80 
x 2 khi x  2 100  x
khi 0  x  2 10
 0x khi 0  x  2
C. T (x)  
. D. T (x)   .
200  80x khi x  2 80
x khi x  2
Trang 1/4 - Mã đề 101 x
Câu 5. Tập xác định D của hàm số y  là: 2  x A. D  \ 0;  2 . B. D  \   0 . C. D  \  
2 . D. D  0;2 .
Câu 6. Phương trình trục đối xứng của Parabol  P 2
: y x  2x 1 là:
A. x  1. B. x  2.  C. x  1. 
D. x  2.
Câu 7. Cho parabol  P 2
: y  3x  2x 1. Điểm nào sau đây là đỉnh của P ?  1 2   1 2   1 2  A. K  ;   . B. J ;   . C. I 0  ;1 . D. H ;    .  3 3   3 3   3 3 
Câu 8. Cho hàm số bậc hai 2
y ax bx c a  0 có đồ thị như hình vẽ sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. 2; . B.  ;  2.
C. 1; . D.  1  ;3.
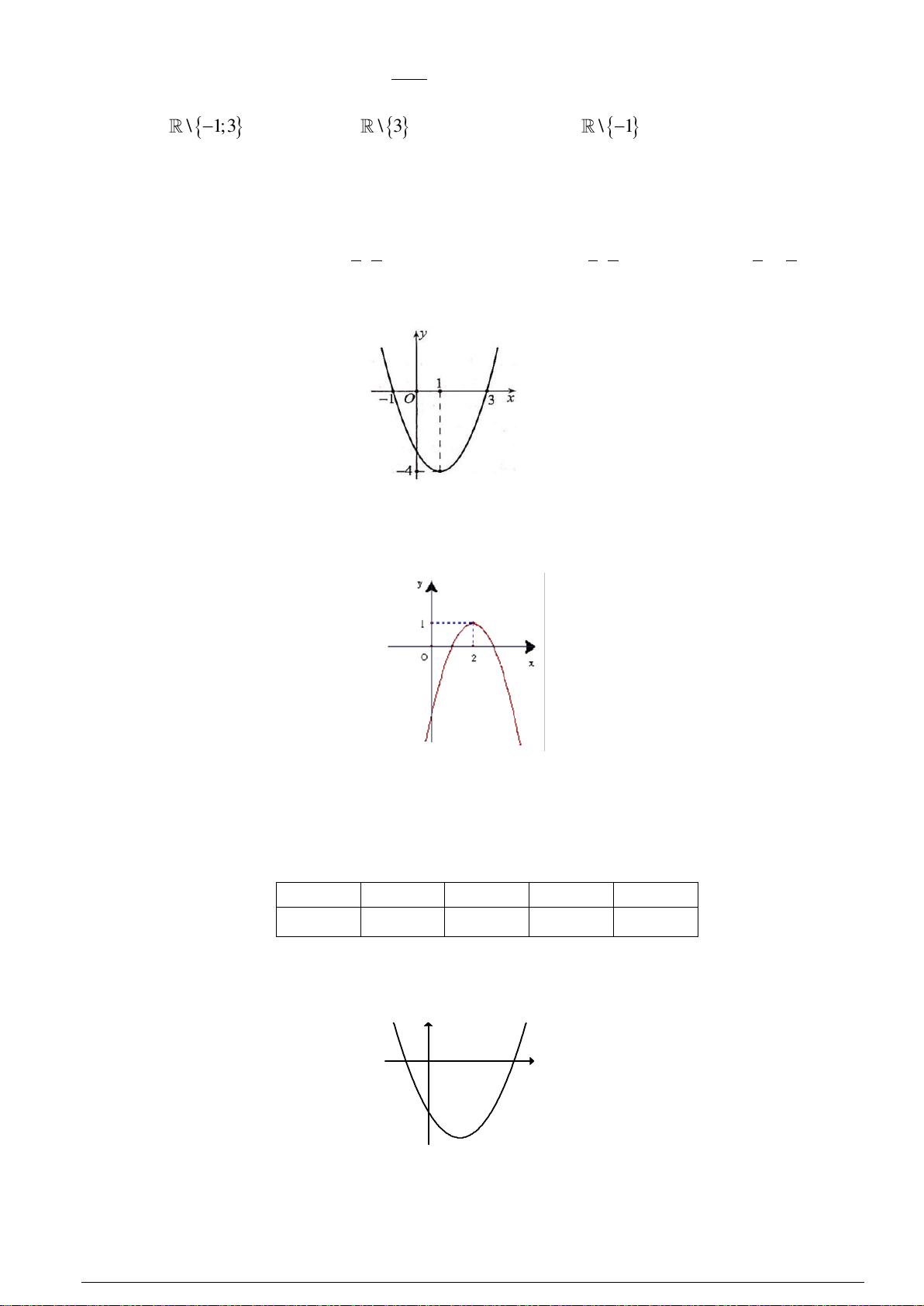
Câu 9. Đồ thị sau đây là đồ thị của hàm số bậc hai nào? A. 2
y x  2x  3. B. 2
y x  2x  3. C. 2
y  x  2x  3. D. 2
y  x  2x  3.
Câu 10. Cho hàm số bậc hai 2
y  x  4x  3. Hãy thay dấu “?” lần lượt bằng các số thích hợp nào để hoàn thành bảng giá trị sau: x 0 1 2 3 y ? ? ? ?
A. 3;  2; 4; 1. B. 3; 5; 6; 7 . C. 3; 6; 7; 6 . D. 3; 5; 1; 2  . Câu 11. Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ. Đặt 2
  b  4ac , tìm dấu của a và  .
A. a  0 ,   0.
B. a  0 ,   0 .
C. a  0 ,   0 .
D. a  0 ,   0
Câu 12. Trong các hàm số sau, hàm nào có đồ thị luôn nằm hoàn toàn phía trên trục hoành?
A. f x 2
 x 3x  4 . B. f x 2
x 3x  2 .
C. f x 2
x 3x  4 . D. f x 2
 x  4x  4 .
Trang 2/4 - Mã đề 101
Câu 13. Cho tam thức bậc hai f x 2
 x  4x  5. Tìm tất cả giá trị của x để f x  0 . A. x  1  ;  5 . B. x  ;   
1 5;  . C. x  5  
;1 . D. x  5  ;  1 .
Câu 14. Cho tam thức f x 2
x  6x  2024 . Khẳng định nào sau đây là đúng?
A. f x  0 khi x  3.
B. f x  0 khi x  3.
C. f x  0 với mọi x .
D. f x  0 khi x  3.
Câu 15. Cho tam thức bậc hai f x  2
 x  5x  6 . Mệnh đề nào sau đây đúng?
A. f x   0  x   2;3  .
B. f x   0  x    ;
 2    3;  .
C. f x   0  x  2;3.
D. f (x)  0  x   2;3  .
Câu 16. Tìm tất cả các giá trị của tham số m để phương trình 2
x  2x m  0 có 2 nghiệm phân biệt.
A. m  4.
B. m 1.
C. m 1.
D. m  4.
Câu 17. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng d : 3
x y  2024  0 ? A. n  (1;3).
B. n  (3; 1).
C. n  (6; 2). D. n  (6; 2  ).
x  2  3t
Câu 18. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng  :  ?  y t A. u  ( 3  ;0). B. u  (3;1). C. u  (6; 2  ). D. u  ( 1  ;3).
Câu 19. Điểm nào sau đây thuộc đường thẳng d : 3
x y  9  0 A. M (3; 0). B. N ( 3  ; 1  ). C. P(6; 2). D. Q(0;9). x  3  tx 1 s
Câu 20. Vị trí tương đối của hai đường thẳng  :  và  : 
, (t, s là các tham số) là: 1
y  1 2t 2 y  3 2s A. Trùng nhau.
B. Cắt nhau nhưng không vuông góc nhau. C. Song song. D. Vuông góc nhau.
Câu 21. Đường thẳng  : 3x  2 y  7  0 song song với đường thẳng nào sau đây?
A. d : 6x  4 y 14  0 . B. d : 3
x  2y  7  0 . C. d :3x  2y  0 .
D. d : 3x  2 y  0 . 1 2 3 4
Câu 22. Đường thẳng  : 3x  2 y  7  0 cắt đường thẳng nào sau đây?
A. d : 6x  4 y 14  0 . B. d : 3
x  2y  7  0 . C. d :3x  2y  0 .
D. d : 3x  2 y  0 . 1 2 3 4
Câu 23. Đường thẳng d : 2x 4 y 1
0 vuông góc với đường thẳng nào sau đây?
A. d : 2x y 14  0 . B. d : 2
x y  7  0 .
C. d : 2x y  7  0 . D. d : 3x  5y  0 . 1 2 3 4
Câu 24. Tìm m để 2 đường thẳng  : 2x y 1  0. và  : 4x my  7  0 vuông góc với nhau? 1 2
A. m  2. B. m  2.  C. m  8.  D. m  8.
Câu 25. Phương trình nào sau đây không phải là phương trình tổng quát một đường thẳng?
A. 3x  2 y  3  0 .
B. 2 y  3  0 .
C. 3x 1  0 . D. 2
3x y  5  0 .
Câu 26. Phương trình tổng quát đường thẳng d đi qua điểm M (1; 2) và có 1 vectơ pháp tuyến n   2;3 là: A. 2x 3y 8 0 . B. 2x 3y 8 0 . C. 4x 6 y 1 0 . D. 2x 3y 12 0 .
x  2  2tx  1 s
Câu 27. Cho hai đường thẳng d :  và d : 
, (t, s là các tham số). Góc giữa hai 2  1 
y  5  4t
y  1 3s
đường thẳng d và d là: 1 2 A. 90 . B. 45. C. 60 . D. 30 .
Trang 3/4 - Mã đề 101
Câu 28. Tìm tọa độ tâm I và bán kính R của đường tròn (C): 2 2
(x 1)  ( y  3)  8 A. I ( 1  ;3), R  8. B. I (1; 3  ), R  8. C. I ( 1
 ;3), R  2 2. D. I (1;3), R  2 2.
Câu 29. Tìm tọa độ tâm I và bán kính R của đường tròn (C: 2 2
x y  8x  4 y  5  0 . A. I (4; 2  ), R  2 5. B. I (4; 2  ), R  5. C. I ( 4  ;2), R  5. D. I ( 4  ;2), R  2 5.
Câu 30. Đường tròn (C) có tâm I (2;3) và qua điểm M(2; 0) có phương trình là: A. 2 2
(x  2)  ( y  3)  9 B. 2 2
(x  2)  ( y  3)  13 C. 2 2
(x  2)  ( y  3)  13 D. 2 2
(x  2)  ( y  3)  9
Câu 31. Phương trình nào sau đây là phương trình chính tắc của đường elip? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1 . B.  1. C.  1 . D.   0 . 9 16 16 9 16 9 25 16
Câu 32. Phương trình nào sau đây là phương trình chính tắc của đường hypebol? 2 2 x y 2 2 x y 2 2 x y 2 2 y x A.   1. B.   1. C.   0 . D.   1. 3 4 9 6 25 16 16 9 2 2 x y
Câu 33. Cho elip (E) có phương trình chính tắc
1 . Tiêu cự của (E) bằng: 25 16 A. 3. B. 6. C. 8. D. 10.
Câu 34. Phương trình nào sau đây là phương trình chính tắc của đường parabol? A. 2 y  4  x . B. 2 y  8x . C. 2 y  4x .
D. y  4x .
Câu 35. Parabol nào sau đây có tham số tiêu bằng 4? A. 2 y  4x . B. 2 y  8x . C. 2 y  2x . D. 2 y  16x .
B. TỰ LUẬN ( 3,0 điểm).
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ Oxy , cho 2 điểm M (5; 4) , N (1; 1) . Viết phương trình tổng
quát đường thẳng  qua 2 điểm M, N.
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ Oxy , cho điểm (3
A ; 4) và đường thẳng d: 4x  3y  2024  0 .
Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
Câu 3 (0,5 điểm). Giải phương trình 2
2x  5x  3  1 x .
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 500 người. Với giá vé 50 000 đồng mỗi vé, trung bình
sẽ có khoảng 200 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến rạp mỗi
ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
------------------------ HẾT ------------------------
Trang 4/4 - Mã đề 101 TRƯỜNG THPT QUẾ SƠN
KIỂM TRA GIỮA KỲ 2- NĂM HỌC 2023-2024 TỔ:TOÁN - TIN
Môn: TOÁN – Lớp 10
Thời gian: 90 phút (Không kể thời gian giao đề) ĐỀ CHÍNH THỨC MÃ ĐỀ 102
(Đề gồm có 04 trang)
A. TRẮC NGHIỆM ( 35 câu x 0,2 = 7,0 điểm).
Học sinh chọn câu trả lời đúng rồi tô vào ô tương ứng trong phiếu làm bài riêng.
Câu 1. Cho biểu đồ nhiệt độ cao nhất trong ngày vào tuần cuối của tháng 3 năm 2024 tại thành phố Tam
Kỳ, tỉnh Quảng Nam. Biểu đồ cho ta một hàm số. Từ biểu đồ, thì nhiệt độ cao nhất vào ngày Thứ 6 là: oC
Biểu đồ nhiệt độ 33 32 31 30 29 28 27 26 25 … 24 Thứ 2 Thứ 3 Thứ 4 Thứ 5 Thứ 6 Thứ 7 Chủ nhậ t Thứ
(Theo https://www.accuweather.com/vi/vn/tam-ky/355712/january-weather). A. 0 29 C . B. 0 30 C . C. 0 31 C . D. 0 32 C .
Câu 2. Xét hai đại lượng ,
x y phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì y không
phải là một hàm số của x? 4 A. 2 x y  4 . B. y  .
C. x  2 y  4 . D. 2
2x y  4 . x
Câu 3. Cho hàm số y f (x) có bảng giá trị sau: x … 2  1 0 1 2 … f (x) … 4  2  0 2 4 …
Hàm số y f (x) là hàm số nào sau đây? A. 2 y x . B. 2 y  x .
C. y  2x .
D. y  2x .
Câu 4. Một hiệu cho thuê xe máy niêm yết giá như sau: giá thuê xe là 100 nghìn đồng cho mỗi ngày trong 3
ngày đầu tiên và 60 nghìn đồng cho mỗi ngày tiếp theo. Gọi T(x) là tổng số tiền phải trả (nghìn đồng) theo
số ngày x mà khách thuê xe. Công thức của T thu được là: 1  00x
khi 0  x  3  100 
x khi 0  x  3
A. T (x)  
. B. T (x)   . 60
  x  3 khi x  3
60x khi x  3 10  0x
khi 0  x  3 1  00x
khi 0  x  3 
C. T (x)  
. D. T (x)   . 30
 0  60x khi x  3 3  00  60 
x 3 khi x  3
Trang 1/4 - Mã đề 102 x 1
Câu 5. Tập xác định D của hàm số y  là: 3  x A. D  \  1  ;  3 . B. D  \   3 . C. D  \  
1 . D. D   1  ;3 .
Câu 6. Phương trình trục đối xứng của Parabol 2
y  x  2x  3 là:
A. x  1. B. x  2.  C. x  1. 
D. x  2.
Câu 7. Cho parabol  P 2
: y  3x  2x 1 . Điểm nào sau đây là đỉnh của P ?  1 2   1 2   1 2  A. I 0  ;1 . B. J ;   . C. K  ;   . D. H ;    .  3 3   3 3   3 3 
Câu 8. Cho hàm số bậc hai 2
y ax bx c a  0 có đồ thị như hình vẽ sau:
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
A. 1;. B.  ;   1 . C.  4  ;. D.  1  ;3.
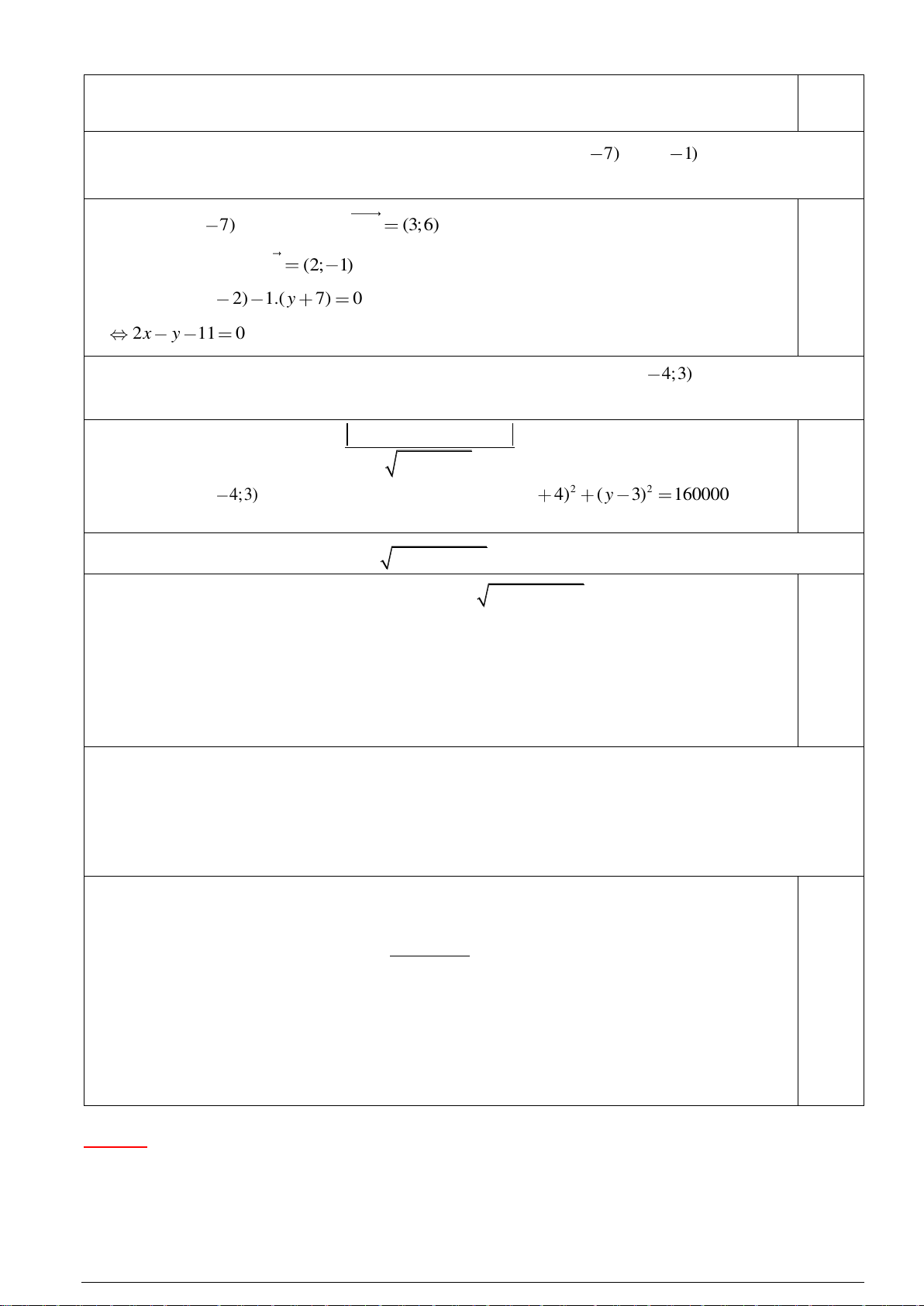
Câu 9. Đồ thị sau đây là đồ thị của hàm số bậc hai nào? A. 2
y x  4x  3. B. 2
y  x  4x  3. C. 2
y x  2x  3. D. 2
y  x  2x  3.
Câu 10. Cho hàm số bậc hai 2
y  x  4x  5. Hãy thay dấu “?” lần lượt bằng các số thích hợp nào để hoàn thành bảng giá trị sau: x 0 1 2 3 y ? ? ? ?
A. 5;  2; 4; 1. B. 5
 ;  2; 1; 7 . C. 5  ; 2; 4; 7 . D. 5  ;  2; 1; 2  . Câu 11. Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ. Đặt 2
  b  4ac , tìm dấu của a và  . y x O
A. a  0 ,   0.
B. a  0 ,   0 .
C. a  0 ,   0 .
D. a  0 ,   0
Câu 12. Trong các hàm số sau, hàm nào có đồ thị luôn nằm hoàn toàn phía dưới trục hoành?
A. f x 2
 x 3x  4 . B. f x 2
x 3x  2 .
C. f x 2
x 3x  4 . D. f x 2
 x  4x  5 .
Trang 2/4 - Mã đề 102
Câu 13. Cho tam thức bậc hai f x 2
 x  4x  5. Tìm tất cả giá trị của x để f x  0 . A. x  1  ;  5 . B. x  ;   
5 1;  . C. x  5  
;1 . D. x  5  ;  1 .
Câu 14. Cho tam thức f x 2
 x  6x  2024. Khẳng định nào sau đây là đúng?
A. f x  0 khi x  3.
B. f x  0 khi x  3.
C. f x  0 khi x  3.
D. f x  0 với mọi x .
Câu 15. Cho tam thức bậc hai f x  2
x  5x  6 . Mệnh đề nào sau đây sai?
A. f x   0  x   2;3  .
B. f x   0  x    ;
 2    3;  .
C. f x   0  x  2;3.
D. f (x)  0  x   2;3  .
Câu 16. Tìm tất cả các giá trị của tham số m để phương trình 2
x  2x m  0 vô nghiệm.
A. m  4.
B. m 1.
C. m 1.
D. m  4.
Câu 17. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng d : 3x y  2024  0 ? A. n  ( 1  ;3).
B. n  (3; 1).
C. n  (3;1). D. n  (6; 2  ).
x  2  3t
Câu 18. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng  :  ? y t A. u  ( 3  ;0).
B. u  (3; 1).
C. u  (6; 2).
D. u  (3;1).
Câu 19. Điểm nào sau đây thuộc đường thẳng d : 3
x y  9  0 A. M (3; 0). B. N ( 3  ; 1  ). C. P(6; 2). D. Q(0;9). x  2  tx 1 s
Câu 20. Vị trí tương đối của hai đường thẳng  :  và  : 
, (t, s là các tham số) là: 1 y  1 2t 2 y  3 2s
A. Vuông góc nhau.
B. Cắt nhau nhưng không vuông góc nhau. C. Song song. D. Trùng nhau.
Câu 21. Đường thẳng  : 3x  2 y  7  0 song song với đường thẳng nào sau đây?
A. d : 6x  4 y 14  0 . B. d : 3x  2 y  0 . C. d : 3
x  2y  7  0 . D. d :3x  2y  0 . 1 2 3 4
Câu 22. Đường thẳng  : 3x  2 y  7  0 cắt đường thẳng nào sau đây?
A. d : 3x  2 y  0 . B. d : 3
x  2y  7  0 . C. d :3x  2y  0 .
D. d : 6x  4 y 14  0 . 1 2 3 4
Câu 23. Đường thẳng d : 2x 4 y 1
0 vuông góc với đường thẳng nào sau đây?
A. d : 2x y 14  0 .
B. d : 2x y 10  0 .
C. d : 2x y  7  0 . D. d : 3x  5y  0 . 1 2 3 4
Câu 24. Tìm m để 2 đường thẳng  : 2x y 1  0. và  : 4x my  7  0 vuông góc với nhau? 1 2
A. m  2. B. m  2.  C. m  8.  D. m  8.
Câu 25. Phương trình nào sau đây không phải là phương trình tổng quát một đường thẳng? A. 2
3x  2 y  3  0 .
B. 2 y  3  0 .
C. 3x 1  0 . D. x  2 y  5  0 .
Câu 26. Phương trình tổng quát đường thẳng d đi qua điểm M (1; 2) và có 1 vectơ pháp tuyến n   2  ;3 là: A. 2x 3y 8 0 . B. 2x 3y 4 0 . C. 2x 3y 1 0 . D. 2x 3y 12 0 . x  2  tx 1 s
Câu 27. Cho hai đường thẳng d :  và d : 
, (t, s là các tham số). Góc giữa hai 2  1 
y  5  2ty 1 3s
đường thẳng d và d là: 1 2 A. 90 . B. 60 . C. 45. D. 30 .
Trang 3/4 - Mã đề 102
Câu 28. Tìm tọa độ tâm I và bán kính R của đường tròn (C): 2 2
(x 1)  ( y  3)  8 A. I ( 1  ;3), R  8. B. I (1; 3  ), R  8. C. I ( 1
 ;3), R  2 2. D. I (1;3), R  2 2.
Câu 29. Tìm tọa độ tâm I và bán kính R của đường tròn (C: 2 2
x y  8x  4 y  5  0 . A. I (4; 2  ), R  2 5. B. I (4; 2  ), R  5. C. I ( 4  ;2), R  5. D. I ( 4  ;2), R  2 5.
Câu 30. Đường tròn (C) có tâm I (2; 3) và qua điểm M( 2
 ; 0) có phương trình là: A. 2 2
(x  2)  ( y  3)  9 B. 2 2
(x  2)  ( y  3)  13 C. 2 2
(x  2)  ( y  3)  13 D. 2 2
(x  2)  ( y  3)  9
Câu 31. Phương trình nào sau đây là phương trình chính tắc của đường elip? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1 . B.  1. C.  1 . D.   0 . 9 6 16 9 6 9 25 16
Câu 32. Phương trình nào sau đây là phương trình chính tắc của đường hypebol? 2 2 x y 2 2 x y 2 2 x y 2 2 y x A.   0 . B.   1. C.   1. D.   1. 3 4 9 6 5 6 16 9 2 2 x y
Câu 33. Cho elip (E) có phương trình chính tắc
1 . Tiêu cự của (E) bằng: 25 9 A. 8. B. 6. C. 9. D. 10.
Câu 34. Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A. y  4x . B. 2 y  8  x . C. 2 y  4x . D. 2 y  4x .
Câu 35. Parabol nào sau đây có tham số tiêu bằng 2? A. 2 y  4x . B. 2 y  8x . C. 2 y  2x . D. 2 y  16x .
B. TỰ LUẬN ( 3,0 điểm).
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ Oxy , cho 2 điểm M (2; 7) , N(5; 1) . Viết phương trình tổng
quát đường thẳng  qua 2 điểm M, N.
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ Oxy , cho điểm ( A
4;3) và đường thẳng d: 3
x  4y  2024  0 .
Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d.
Câu 3 (0,5 điểm). Giải phương trình 2
2x  7x  5  1 x .
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 400 người. Với giá vé 50 000 đồng mỗi vé, trung bình
sẽ có khoảng 160 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 40 người đến rạp mỗi
ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
------------------------ HẾT ------------------------
Trang 4/4 - Mã đề 102 Đề\câu 101 102 103 104 1 A C D B 2 C D A A 3 D C D C 4 B D D B 5 C B B D 6 C A D A 7 A B A A 8 A A C C 9 A B B D 10 C D D C 11 D C B B 12 C A D A 13 C B A B 14 C D C D 15 A A D C 16 B C D D 17 D B B D 18 B D C C 19 D A A A 20 A D B A 21 C B C B 22 D A D C 23 C B C C 24 C D A B 25 D A A D 26 A B A A 27 B C A C 28 C D B A 29 B C C B 30 A D B D 31 C A C B 32 A C D A 33 B A A B 34 C D C D 35 B A B C Trường THPT Quế Sơn
Hướng dẫn chấm Toán 10 Tổ Toán-Tin GK2-2023-2024 Đề 101-103 Điểm
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ Oxy , cho 2 điểm M (5; 4) , N (1; 1) . Viết phương trình
tổng quát đường thẳng qua 2 điểm M, N.
+ Đường thẳng  qua M (5; 4) và có VTCP MN ( 4;3) 0,25 + Nên  có VTPT n (3; 4) 0,25 + PTTQ  : 3(x 5) 4( y 4) 0 0,25 + 3x 4 y 1 0 0,25
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ Oxy , cho điểm (3
A ; 4) và đường thẳng d:
4x  3y  2024  0 . Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d. 4.3  3( 4)   2024
+ (C) có bán kính R = d  , A d    400 0,25 2 2 4  ( 3  ) . + (C) có tâm (3
A ; 4) và có bán kính R=400  Pt (C): 2 2 (x 3) ( y 4) 160000 0,25
Câu 3 (0,5 điểm). Giải phương trình 2
2x  5x  3  1 x .
+ Bình phương 2 vế phương trình đã cho ta được:  x x  2 2 2 2 5 3  (1 x) 2 2
 2x  5x  3 1 2x x x  2
x  3x  2  1 0   0,25 x  2
+ Thử lại ta thấy x = 1 là nghiệm của phương trình đã cho còn x = 2 không phải là nghiệm của
phương trình đã cho. Vậy phương trình đã cho có 1 nghiệm x = 1. 0,25
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 500 người. Với giá vé 50 000 đồng, trung bình sẽ
có khoảng 200 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo
sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến
rạp mỗi ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
+ Gọi x (nghìn đồng) là giá mỗi vé bán ra để doanh thu đạt lớn nhất 0  x  50 .
Suy ra số tiền giảm giá mỗi vé so với mức giá cũ là: 50  x (nghìn đồng) 0,25 5050  x
+ Số người tăng lên khi giảm giá vé là:  550  x 10 0,25
+ Số người đến rạp chiếu phim mỗi ngày khi giảm giá vé là: 200 + 550  x  5  x  450
Doanh thu mỗi ngày khi giá vé x (nghìn đồng) là: T x 2  5  x  450x 0,2 5
+ Ta có T(x) làm hàm số bậc 2 có đồ thị là parabol (P). T(x) đạt GTLN tại x0 là hoành độ
đỉnh của (P) , khi đó x0 = 45. 0,25
Vậy doanh thu lớn nhất trong ngày (là 10.125.000 đồng) khi giá mỗi vé là 45 000 đồng
Đáp án Tự luận Toán 10_GK2_23-24 Đề 102-104 Điểm
Câu 1 (1,0 điểm). Trong mặt phẳng tọa độ Oxy , cho 2 điểm M (2; 7) , N(5; 1) . Viết phương trình
tổng quát đường thẳng qua 2 điểm M, N.
+  qua M (2; 7) và có 1 VTCP MN (3;6) 0,25
+ Suy ra  có 1 VTPT n (2; 1) 0,25 + PTTQ  : 2(x 2) 1.( y 7) 0 0,25 + 2x y 11 0 0,25
Câu 2 (0,5 điểm). Trong mặt phẳng tọa độ Oxy , cho điểm ( A
4;3) và đường thẳng d: 3
x  4y  2024  0 . Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng d. ( 3  ).( 4)   4.3  2024
+ (C) có bán kính R = d  , A d    400 2 2 ( 3  )  4 . 0,25 + (C) có tâm ( A
4;3) và có bán kính R  400  Pt (C): 2 2 (x 4) ( y 3) 160000 0,25
Câu 3 (0,5 điểm). Giải phương trình 2
2x  7x  5  1 x .
+ Bình phương 2 vế phương trình đã cho ta được:  x x  2 2 2 2 7 5  (1 x) 2 2
 2x  7x  5 1 2x x x 2
x  5x  4  1 0   x  4 0,25
+ Thử lại ta thấy x = 1 là nghiệm của phương trình đã cho còn x = 4 không phải là nghiệm của
phương trình đã cho. Vậy phương trình đã cho có 1 nghiệm x = 1. 0,25
Câu 4 (1,0 điểm). Một rạp chiếu phim có sức chứa 400 người. Với giá vé 50 000 đồng mỗi vé, trung
bình sẽ có khoảng 160 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim
đã khảo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 40
người đến rạp mỗi ngày. Tìm mức giá mỗi vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
+ Gọi x (nghìn đồng) là giá mỗi vé bán ra để doanh thu đạt lớn nhất 0  x  50 .
Suy ra số tiền giảm giá mỗi vé so với mức giá cũ là: 50  x (nghìn đồng) 0,25 40 50  x
+ Số người tăng lên khi giảm giá vé là:  450  x 10 0,25
+ Số người đến rạp chiếu phim mỗi ngày khi giảm giá vé là: 160 + 450  x  4  x  360
Doanh thu mỗi ngày khi giá vé x (nghìn đồng) là: T x 2  4  x  360x 0,25
+ Ta có T(x) làm hàm số bậc 2 có đồ thị là parabol (P). T(x) đạt GTLN tại x0 là hoành độ đỉnh của (P), khi đó x 0 = 45.
Vậy doanh thu lớn nhất trong ngày (là 8.100. 000 đồng) khi giá mỗi vé là 45 000 đồng 0,25
Ghi chú: Học sinh giải theo cách khác mà đúng thì Thầy, Cô cho điểm tối đa theo thang điểm đã qui định.
Đáp án Tự luận Toán 10_GK2_23-24
Document Outline

  • 101-Toan-10-GK2-23-24
  • 102-Toan-10-GK2-23-24
  • Dap-an-Trac-nghiem-Toan-10-GK2_23-24
    • Sheet1
  • Dap-an-TL-Toan-10-_GK2_23-24