Đề thi giữa kỳ 2 Toán 11 năm 2023 – 2024 trường THPT Nguyễn Chí Thanh – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kỳ 2 môn Toán 11 năm học 2023 – 2024 trường THPT Nguyễn Chí Thanh, thành phố Hồ Chí Minh; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile M. Hậu
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
TRƯỜNG THPT NGUYỄN CHÍ THANH
Đề chính thức
(Đề thi có 01 trang)
ĐỀ KIỂM TRA GIỮA HỌC KỲ II (2023 – 2024)
Môn: TOÁN 11A, 11A1, 11B, 11D
Thời gian làm bài: 60 phút
(không tính thời gian phát đề)
Bài 1. (1 điểm) Cho
0a
, rút gọn các biểu thức sau:
a)
17
1
36
2
a a a
b)
1
1
3
2
6
4
.:a a a
Bài 2. (1 điểm) Tính đạo hàm của các hàm số sau:
a)
3
5
2 4 1y x x
x
= − + −
b)
2
.logy x x=
Bài 3. (1 điểm) Tìm tập xác định của hàm số
Bài 4. (1 điểm) Đặt
35
log 4, log 4ab==
. Hãy biểu diễn
12
log 80
theo a và b.
Bài 5. (2 điểm) Giải phương trình và bất phương trình sau:
a)
2
34
34
1
2
2
x
xx
+
++

=


b)
( ) ( )
31
3
2log 1 1 og 7x l x+ − +
Bài 6. (1 điểm) Với nước biển có nồng độ muối
30%
, nhiệt độ
( )
TC
của nước biển được tính bởi công
thức
7,9ln(1,0245 ) 61,84Td= − +
trong đó
( )
3
/d g cm
là khối lượng riêng của nước biển.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Biết vùng biển khơi mặt ở một khu vực có nồng độ muối
30%
và nhiệt độ là
8 C
. Tính khối
lượng riêng của nước biển ở vùng biển đó (làm tròn đến 4 chữ số thập phân sau dấu phẩy).
Bài 7. (3 điểm) Cho hình chóp
.S ABCD
có
( )
,SA ABCD⊥
đáy là hình chữ nhật
ABCD
với
; 3, 3AB a AD a SA a= = =
.
a) Chứng minh tam giác SBC vuông tại B.
b) Gọi H là hình chiếu vuông góc của A lên cạnh BD. Chứng minh
( ) ( )
SAH SBD⊥
.
c) Tính góc giữa mặt phẳng
( )
SBD
và mặt phẳng
( )
.SAB
−−−− HẾT −−−−
Thí sinh không sử dụng tài liệu. Thầy, Cô coi thi không giải thích gì thêm.
Họ và tên: ………………………………………. Số báo danh: ………………..…
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC LỚP 11 A
1
Cho
0a
, rút gọn các biểu thức sau:
a)
17
1
36
2
a a a
b)
1
1
3
2
6
4
.:a a a
1đ
a)
1 7 1 1 7
1
2
3 6 3 2 6
2
a a a a a
++
= =
b)
1
1
3
2
6
4
.:a a a
=
2 1 2 1 1
13
3 6 3 4 6
44
:a a a a a
+−
= =
0.25x4
2
Tính đạo hàm của các hàm số sau:
a)
3
5
2 4 1y x x
x
= − + −
b)
2
.logy x x=
1đ
a)
/2
2
52
6yx
x
x
= + +
( ) ( )
//
/
2 2 2
1
log log log
ln2
y x x x x x= + = +
0.25x2
0.25x2
3
Tìm tập xác định của hàm số
( )
2
log 4 9yx=−
1đ
Điều kiện:
2
3
2
4 9 0
3
2
x
x
x
−
−
Vậy tập xác định:
33
;;
22
D
= − − +
0.25x4
4
Đặt
35
log 4, log 4ab==
. Hãy biểu diễn
12
log 80
theo a và b
1đ
( )
( )
( )
( )
2
2
4
4 4 4
12
4 4 4 4
1
2
log 5.4
12
log 80 log 5 log 4
log 80
1
log 12 log 3.4 log 3 log 4 1
1
ab
b
ba
a
+
+
+
= = = = =
++
+
0.25x4
5
Giải phương trình và bất phương trình sau:
a)
2
34
34
1
2
2
x
xx
+
++

=


b)
( ) ( )
31
3
2log 1 1 og 7x l x+ − +
1đ
22
34
3 4 3 4 3 4 2
2
1
2 2 2 6 8 0
4
2
x
x x x x x
x
xx
x
+
+ + + + − −
=−

= = + + =

=−

0.25x2
0.25x2
b) Điều kiện :
( )
1 0 1
1*
7 0 7
xx
x
xx
+ −

−

+ −

.
( ) ( ) ( ) ( )
( ) ( )
22
3 3 3 3 3
2
2
log 1 log 3 log 7 log 1 log 3 7
1 3 7 ... 20 0 4 5
bpt x x x x
x x x x x
+ + + + +
+ + − − −
Kết hợp với điều kiện (*), ta được tập nghiệm của bất phương trình là
( 1;5]S =−
6
Với nước biển có nồng độ muối
30%
, nhiệt độ
( )
TC
của nước biển được tính bởi công
thức
7,9ln(1,0245 ) 61,84Td= − +
trong đó
( )
3
/d g cm
là khối lượng riêng của nước biển.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Biết vùng biển khơi mặt ở một khu vực có nồng độ muối
30%
và nhiệt độ là
8 C
. Tính
khối lượng riêng của nước biển ở vùng biển đó (làm tròn đến 4 chữ số thập phân sau
dấu phẩy).
1đ
Theo giả thiết, với
8T =
ta có phương trình:
2692
7,9ln(1,0245 ) 61,84 8 ln(1,0245 )
395
dd
−
− + = − =
(0,25đ)
2692
395
1,0245 de
−
− =
(0,25đ)
2692
395
1,0245 .de
−
= −
(0,25đ)
Suy ra khối lượng riêng của nước biển ở vùng biển đó là:
3
1,0234 /d g cm
.(0,25đ)
0.25
0.25
0.25
0.25
7
Cho hình chóp
.S ABCD
có
( )
,SA ABCD⊥
đáy là hình chữ nhật
ABCD
với
; 3, 3AB a AD a SA a= = =
.
a) Chứng minh tam giác SBC vuông tại B.
b) Gọi H là hình chiếu vuông góc của A lên cạnh BD. Chứng minh
( ) ( )
SAH SBD⊥
.
c) Tính góc giữa mặt phẳng
( )
SBD
và mặt phẳng
( )
.SAB
1đ
a) Ta có:
(S ;BC )
:
BC AB ABCD laøhcn
BC SA A ABCD ABCD
SAB SA AB A
BC SAB taïi B
Mà
( )
SB SAB SB BC ⊥
. Suy ra tam giác SBC vuông tại B.
0.25x4
1đ
b) Ta có:
(S ;B )
:
AH BD gt
BD SA A ABCD H ABCD
SAH SA AH A
BD SAH
Mà
( )
BD SBD
( ) ( )
SBD SAH⊥
0.25x4
1đ
c) Kẻ   tại I. Chứng minh được  󰇛󰇜
Mặt khác  󰇛󰇜
Vậy
󰇛

󰇜
󰇛

󰇜
󰇛󰇜
Xét tam giác ABD vuông tại A:




Xét tam giác vuông SHA vuông tại A ta có:









Xét tam giác vuông AID vuông tại I ta có:  







Vậy
󰇛

󰇜
󰇛

󰇜
󰇛
 
󰇜



0.25x4
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
ĐỀ KIỂM TRA GIỮA HỌC KỲ II (2023 – 2024)
TRƯỜNG THPT NGUYỄN CHÍ THANH
Môn: TOÁN 11A, 11A1, 11B, 11D Đề chính thức
Thời gian làm bài: 60 phút
(Đề thi có 01 trang)
(không tính thời gian phát đề)
Bài 1. (1 điểm) Cho a  0 , rút gọn các biểu thức sau: 1 1 7 1 1 3 2 a) 3 2 6 a a a b) 4 6
a .a : a
Bài 2. (1 điểm) Tính đạo hàm của các hàm số sau: 5 a) 3 y = 2x − + 4 x −1 b) y = . x log x x 2
Bài 3. (1 điểm) Tìm tập xác định của hàm số y = ( 2 log 4x − 9)
Bài 4. (1 điểm) Đặt a = log 4,b = log 4 . Hãy biểu diễn log 80 theo a và b. 3 5 12
Bài 5. (2 điểm) Giải phương trình và bất phương trình sau: 3x+4  x + x+  1 a) 2 3 4 2 =   b) 2log x +1  1− o l g x + 7 3 ( ) 1 ( )  2  3
Bài 6. (1 điểm) Với nước biển có nồng độ muối 30% , nhiệt độ T ( C ) của nước biển được tính bởi công
thức T = 7,9 ln(1, 0245 − d ) + 61,84 trong đó d ( 3
g / cm ) là khối lượng riêng của nước biển.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Biết vùng biển khơi mặt ở một khu vực có nồng độ muối 30% và nhiệt độ là 8C . Tính khối
lượng riêng của nước biển ở vùng biển đó (làm tròn đến 4 chữ số thập phân sau dấu phẩy).
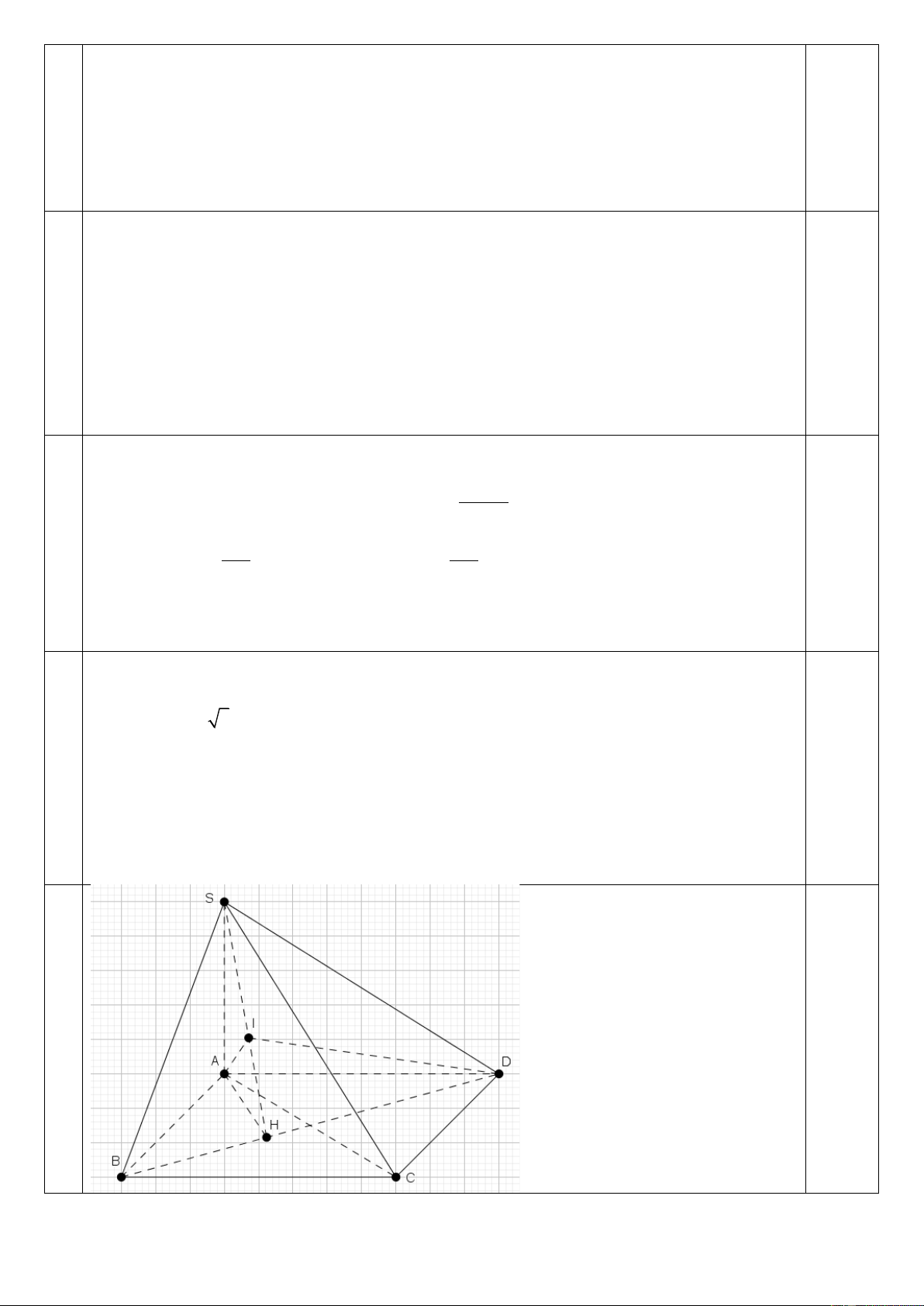
Bài 7. (3 điểm) Cho hình chóp S.ABCD có SA ⊥ ( ABCD), đáy là hình chữ nhật ABCD với AB = ;
a AD = a 3, SA = 3a .
a) Chứng minh tam giác SBC vuông tại B.
b) Gọi H là hình chiếu vuông góc của A lên cạnh BD. Chứng minh (SAH ) ⊥ (SBD) .
c) Tính góc giữa mặt phẳng (SBD) và mặt phẳng (SAB).
−−−− HẾT −−−−
Thí sinh không sử dụng tài liệu. Thầy, Cô coi thi không giải thích gì thêm.
Họ và tên: ……………………………………….
Số báo danh: ………………..…
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC LỚP 11 A 1
Cho a  0 , rút gọn các biểu thức sau: 1 1 7 1 1 3 2 a) 3 2 6 a a a b) 4 6
a .a : a 1đ 1 1 7 1 1 7 + + 0.25x4 a) 2 3 2 6 3 2 6
a a a = a = a 1 1 2 1 1 2 1 1 3 + − b) 3 2 4 6
a .a : a = 3 4 6 3 4 6 4
a a : a = a = a 2 Tính đạ
o hàm của các hàm số sau: 5 a) 3 y = 2x − + 4 x −1 b) y = . x log x x 2 1đ 5 2 0.25x2 a) / 2 y = 6x + + 2 x x
y = ( x)/ log x + x(log x)/ 1 / = log x + 0.25x2 2 2 2 ln 2 3
Tìm tập xác định của hàm số y = ( 2 log 4x − 9) 1đ  3 0.25x4 x  −  Điề 2 u kiện: 2 4x − 9  0   3 x   2  3   3 
Vậy tập xác định: D = − ;  −  ; +      2   2  4
Đặt a = log 4,b = log 4. Hãy biểu diễn log 80 theo a và b 3 5 12 1đ + log 80 ( 1 2 ) 2 2 log 5.4 + + 4 log 5 log 4 a (1 2b) 4 4 4 0.25x4 log 80 b = = = = = 12 log 12 log 3.4 log 3 + log 4 1 b 1 + a 4 4 ( ) 4 4 ( ) +1 a 5
Giải phương trình và bất phương trình sau: 3x+4  x + x+  1 a) 2 3 4 2 =   b) 2log x +1  1− o l g x + 7 3 ( ) 1 ( )  2  3 1đ 3x+4    = − 0.25x2 2 2 x x + x+ 1 2 3 4 x +3x+4 3 − x−4 2 2 =  2 = 2
x + 6x + 8 = 0      2  x = 4 − 0.25x2 x +1  0 x  1 − b) Điều kiện :     x  1 − (*) . x + 7  0 x  7 −
bpt  log ( x + )2 1
 log 3 + log (x + 7)  log (x + )2 1  log 3 x + 7 3 3 3 3 3 ( )  (x + )2 1  3(x + 7) 2
 ...  x − x − 20  0  4 −  x  5
Kết hợp với điều kiện (*), ta được tập nghiệm của bất phương trình là S = ( 1 − ;5] 6
Với nước biển có nồng độ muối 30% , nhiệt độ T ( C ) của nước biển được tính bởi công
thức T = 7,9 ln(1, 0245 − d ) + 61,84 trong đó d ( 3
g / cm ) là khối lượng riêng của nước biển.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Biết vùng biển khơi mặt ở một khu vực có nồng độ muối 30% và nhiệt độ là 8C . Tính
khối lượng riêng của nước biển ở vùng biển đó (làm tròn đến 4 chữ số thập phân sau dấu phẩy).
1đ Theo giả thiết, với T = 8 ta có phương trình: 0.25 2692 −
7, 9 ln(1, 0245 − d ) + 61,84 = 8  ln(1, 0245 − d ) = (0,25đ) 395 0.25 2692 − 2692 − 395
 1,0245 − d = e (0,25đ) 395
d =1,0245 − e .(0,25đ) 0.25
Suy ra khối lượng riêng của nước biển ở vùng biển đó là: 3
d  1, 0234 g / cm .(0,25đ) 0.25 7
Cho hình chóp S.ABCD có SA ⊥ ( ABCD), đáy là hình chữ nhật ABCD với AB = ;
a AD = a 3, SA = 3a .
a) Chứng minh tam giác SBC vuông tại B.
b) Gọi H là hình chiếu vuông góc của A lên cạnh BD. Chứng minh (SAH ) ⊥ (SBD) .
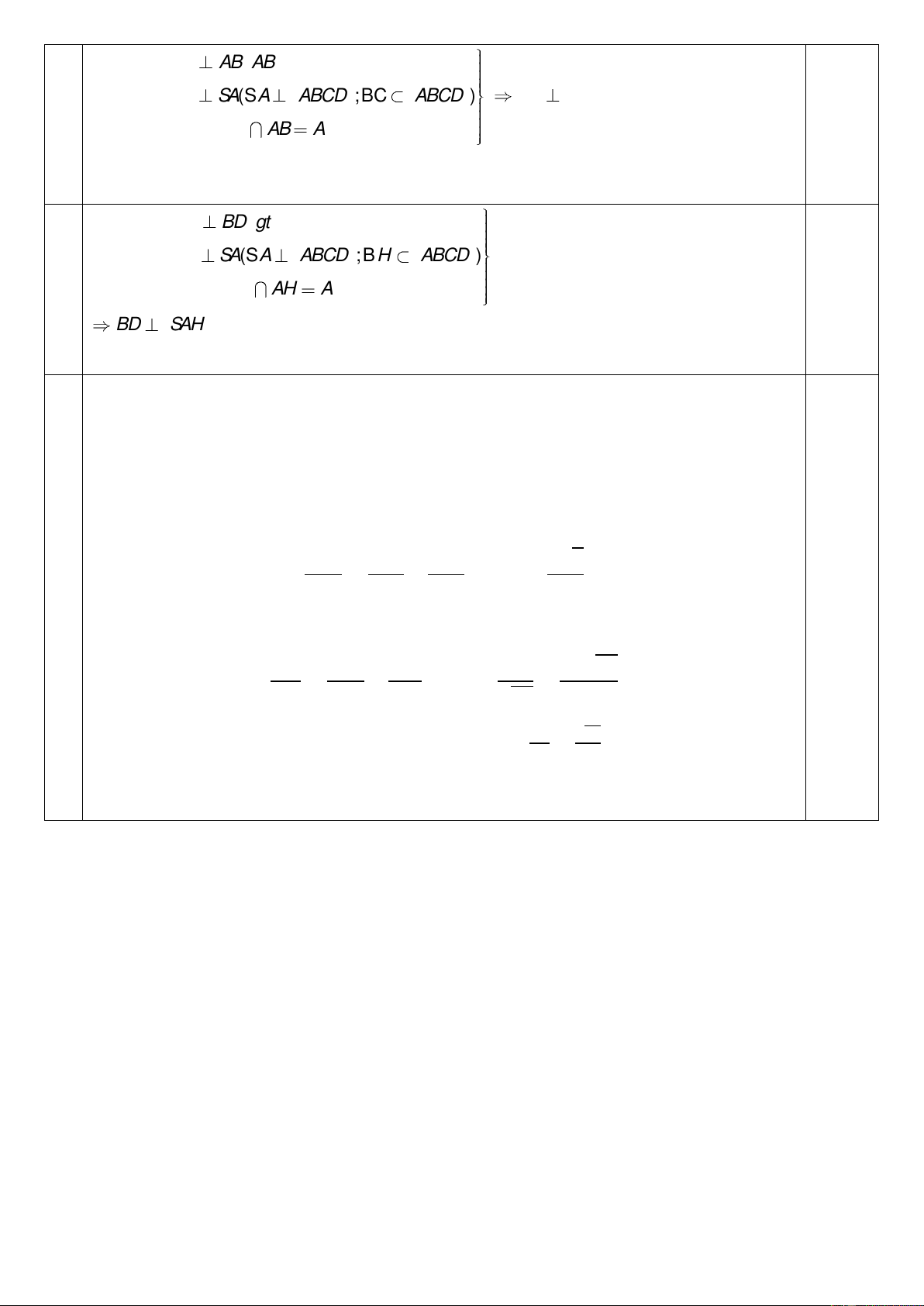
c) Tính góc giữa mặt phẳng (SBD) và mặt phẳng (SAB). 1đ BC AB ABCD laøhcn 0.25x4 a) Ta có: BC S ( A SA ABCD ; BC ABCD ) BC SAB taïi B SAB : SA AB A
Mà SB  (SAB)  SB ⊥ BC . Suy ra tam giác SBC vuông tại B. 1đ AH BD gt 0.25x4 b) Ta có: BD S ( A SA ABCD ; BH ABCD ) SAH : SA AH A BD SAH
Mà BD  (SBD)  (SBD) ⊥ (SAH )
1đ c) Kẻ 𝐴𝐼 ⊥ 𝑆𝐻 tại I. Chứng minh được 𝐴𝐼 ⊥ (𝑆𝐵𝐷) 0.25x4
Mặt khác 𝐴𝐷 ⊥ (𝑆𝐴𝐵)
Vậy ((𝑆𝐴𝐵); (𝑆𝐵𝐷)) = (𝐴𝐷; 𝐴𝐼)
Xét tam giác ABD vuông tại A: 1 1 1 𝑎√3 = + ⇒ 𝐴𝐻 = 𝐴𝐻2 𝐴𝐵2 𝐴𝐷2 2
Xét tam giác vuông SHA vuông tại A ta có: 1 1 1 3𝑎 3𝑎√13 = + ⇒ 𝐴𝐼 = = 𝐴𝐼2 𝐴𝐻2 𝐴𝑆2 √13 13 𝐴𝐼
Xét tam giác vuông AID vuông tại I ta có: cos 𝐼𝐴𝐷 ̂ = = √39 ⇒ 𝐼𝐴𝐷 ̂ ≈ 61017′ 𝐴𝐷 13
Vậy ((𝑆𝐴𝐵); (𝑆𝐵𝐷)) = (𝐴𝐷; 𝐴𝐼) = 𝐼𝐴𝐷 ̂ ≈ 61017′