Đề thi giữa kỳ | Môn Tối ưu hóa - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi môn: Tối ưu hóa KHOA KINH TẾ Mã môn học: MAOP230706 BM QTKD Đề số 4 Thời gian: 60 phút
Được phép sử dụng tài liệu Bài 1 (4đ):
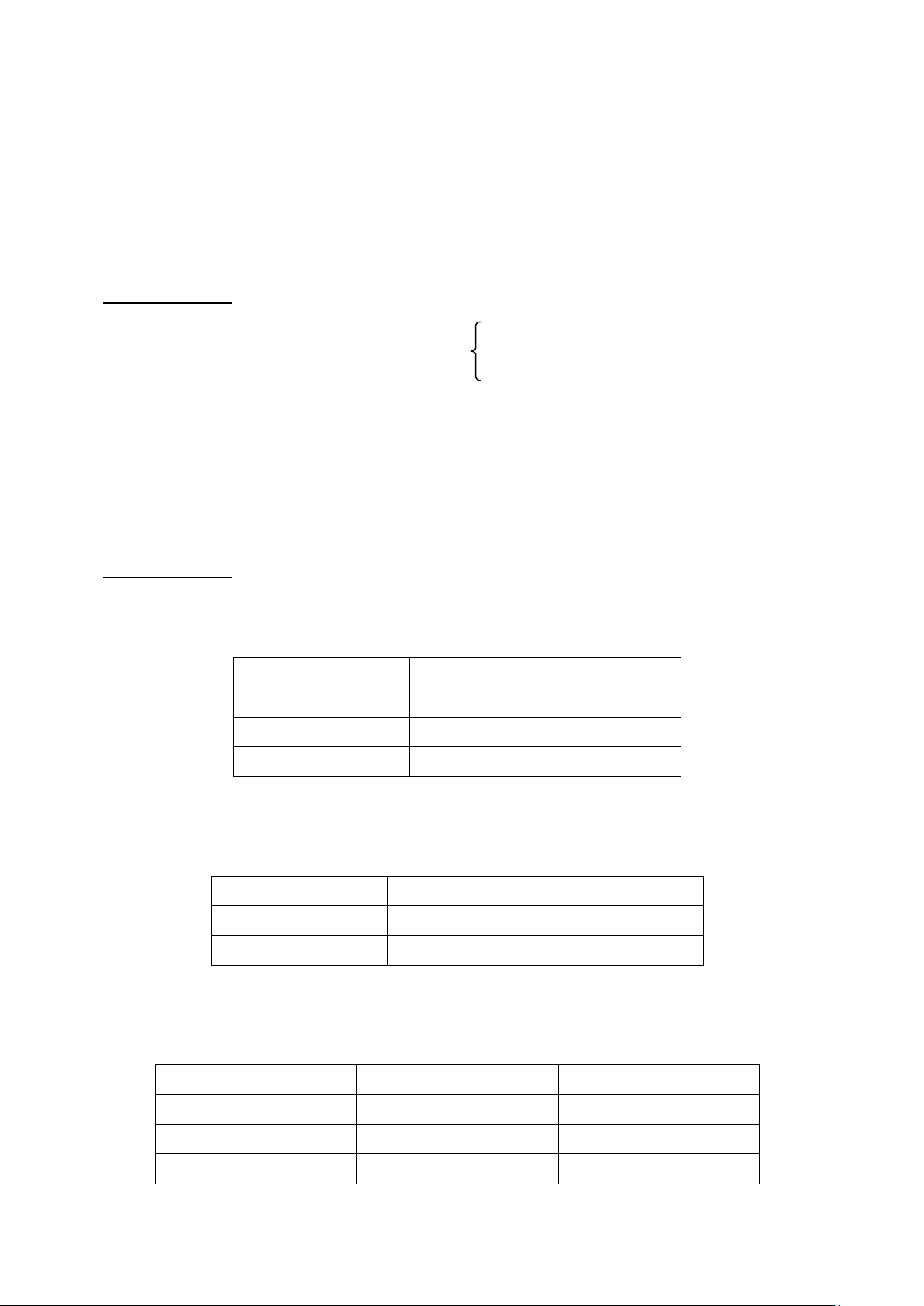
Cho bài toán gốc (P): (1) f(x) = 5x1 + 10x2 + 7x3 + 3x4 ® min x1 + 4x2 + x3 + 2x4 ≤ 6 2x1 + + x3 + 4x4 = 9 3x1 + 2x2 + x4 ≥ 10
x1 ³ 0 , x2 ³ 0 , x3 ³ 0, x4 ³ 0
a) Lập bài toán đối ngẫu (D) tương ứng của (P).
b) Giải bài toán (P). Suy ra kết quả bài toán (D). Bài 2 (3đ):
Một công ty sản xuất ra 1 loại hàng, có 3 nhà máy sản xuất đặt tại 3 địa điểm khác nhau.
Biết công suất ở các nhà máy cho ở bảng sau: Nhà máy Công suất A1 150 A2 70 A3 180
Sản phẩm của công ty được phân phối đến 3 thị trường với mức tiêu thụ hàng tháng như sau: Thị trường Khả năng tiêu thụ B1 120 B2 200 B3 180
Biết chi phí trên 1 sản phẩm từ nhà máy đến thị trường tương ứng như sau: (đơn vị: 1.000 đ/ sản phẩm) B1 B2 B3 A1 10 7 9 A2 12 8 5 A3 10 6 11 Yêu cầu:
Hãy xác định kế hoạch phân phối sao cho tổng chi phí nhỏ nhất với điều kiện thị trường B1
phải tiêu thụ hết sản phẩm và tuyến đường A2 đến B3 bị cấm. Bài 3 (3đ):
Một công ty may mặc ký hợp đồng giao cho khách hàng 36.000 bộ đồ bảo hộ lao động
(mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có ba xí nghiệp I, II, III với năng suất trung
bình của mỗi xí nghiệp khi sản xuất quần, áo, găng tay được cho trong bảng sau (áo/ngày,
quần/ngày, găng tay/ngày) S.Phẩm Quần Áo Găng tay X.Nghiệp 1 1 2 XN I: 1 180 200 300 XN II: 2 80 110 160 XN III: 1 120 230 240 Yêu cầu: a.
Hỏi phải phân công thời gian sản xuất của các xí nghiệp như thế nào để trong một
ngày tạo ra được nhiều bộ đồ bảo hộ lao động nhất? Ước tính thời gian trung bình để hoàn
thành 36.000 bộ đồ bảo hộ lao động. b.
Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các xí nghiệp như thế
nào để hoàn thành hợp đồng sớm nhất? lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi môn: Tối ưu hóa HK 2 NH 2021-2022
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO Mã môn học: MAOP230706 BM QTKD Đề số: 2 Thời gian: 60 phút
Được phép sử dụng tài liệu
Câu 1 (4 điểm) Cho bài toán gốc (P): f(x) = 2x1 + 3x2 + 2x3 ® min x1 + x2 + 2x3 ≤ 8 x1 + 2x2 + x3 = 2 2x1 + 4x2 + 4x3 ≤ 8 x1 ³ 0 , x2 ³ 0 , x3 ³ 0
a) Lập bài toán đối ngẫu (D) tương ứng của (P).
b) Giải bài toán gốc (P). Từ kết quả của bài toán gốc (P), hãy suy ra PATƯ của bài toán đối ngẫu (D)
Câu 2 (3 điểm )
Một công ty sản xuất ra 1 loại hàng, có 3 nhà máy sản xuất đặt tại 3 địa điểm khác nhau.
Biết công suất ở các nhà máy cho ở bảng sau: Nhà máy
Công suất (1000 sp/ tháng) A1 140 A2 130 A3 100
Sản phẩm của công ty được phân phối đến 2 thị trường với mức tiêu thụ hàng tháng như sau: Thị trường
Khả năng tiêu thụ (1000 sp/ tháng) B1 120 B2 160
Biết chi phí vận chuyển 1 sản phẩm từ nhà máy đến thị trường tương ứng như sau: (đơn vị: 1.000 đ/ sản phẩm) B1 B2 A1 8 9 A2 6 5 A3 7 10 Yêu cầu: lOMoAR cPSD| 58794847
Hãy xác định kế hoạch phân phối sao cho tổng chi phí nhỏ nhất với điều kiện nhà máy
A1 phải sản xuất hết công suất, và tuyến đường A2 đến B2 bị cấm.
Câu 3: (3 điểm)
Một xưởng gia công may mặc ký hợp đồng giao cho khách hàng 6000 bộ đồ bảo hộ lao
đông( mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có 2 loại máy với năng suất trung
bình của mỗi máy khi sản xuất quần, áo, găng tay được cho trong bảng sau
(áo/ngày, quần/ngày, găng tay/ngày) S.Phẩm Quần Áo Găng tay 1 1 2 Máy I: 4 60 80 130 Máy II: 3 40 80 120
a) Hỏi phải phân công thời gian sản xuất của các máy như thế nào để trong một ngày
tạo ra được nhiều bộ đồ bảo hộ lao đồng nhất? Ước tính thời gian trung bình để
hoàn thành hợp đồng (2,5 điểm)
b) Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các máy như thế nào
để hoàn thành hợp đồng sớm nhất? (0.5 điểm)
Ở bài toán SXĐB: SV trình bày kết quả ở dạng số, lấy 2 chữ số thập phân sau
dấu phẩy; KHÔNG trình bày ở dạng phân số.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 1.2]: Sử dụng một số phương pháp để giải bài toán quy hoạch tuyến Câu 1 tính
[CĐR 2.1]: Sử dụng thuật toán thế vị để giải bài toán vận tải Câu 2
[CĐR 3.1]: Sử dụng thuật toán nhân tử để giải bài toán sản xuất đồng bộ Câu 3
TP HCM, ngày …tháng…năm… Duyệt đề
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi môn: Tối ưu hóa HK 2 NH 2021-2022 KHOA KINH TẾ Mã môn học: MAOP230706 BM QTKD Đề số: 2 Thời gian: 75 phút
Được phép sử dụng tài liệu lOMoAR cPSD| 58794847
Câu 1 (4 điểm) Cho bài toán gốc (P): f(x) = 3x1 + 2x2 + 2x3 ® max x1 + 2x2 + 2x3 = 4 2x1 + x2 + 2x3 ≤ 8 x1 + x2 + 2x3 ≤ 6 x1 ³ 0 , x2 ³ 0 , x3 ³ 0
a) Lập bài toán đối ngẫu (D) tương ứng của (P).
b) Giải bài toán gốc (P). Từ kết quả của bài toán gốc (P), hãy suy ra PATƯ của bài toán đối ngẫu (D)
Câu 2 (3 điểm )
Một công ty sản xuất ra 1 loại hàng, có 2 nhà máy sản xuất đặt tại 2 địa điểm khác nhau.
Biết công suất ở các nhà máy cho ở bảng sau: Nhà máy
Công suất (1000 sp/ tháng) A1 120 A2 160
Sản phẩm của công ty được phân phối đến 3 cửa hàng với mức tiêu thụ hàng tháng như sau: Thị trường
Khả năng tiêu thụ (1000 sp/ tháng) B1 120 B2 110 B3 130
Biết chi phí của 1 sản phẩm từ nhà máy đến thị trường tương ứng như sau: (đơn vị: 1.000 đ/ sản phẩm) B1 B2 B3 A1 12 14 12 A2 10 11 9 Yêu cầu:
Hãy xác định kế hoạch phân phối sao cho tổng chi phí thấp nhất với điều kiện cửa hàng
B1 phải nhận đủ hàng, và tuyến đường A2 đến B3 bị cấm.
Câu 3: (3 điểm)
Một xưởng gia công may mặc ký hợp đồng giao cho khách hàng 5000 bộ đồ bảo hộ lao
đông( mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có 2 loại máy với năng suất trung
bình của mỗi máy khi sản xuất quần, áo, găng tay được cho trong bảng sau
(áo/ngày, quần/ngày, găng tay/ngày) lOMoAR cPSD| 58794847 S.Phẩm Quần Áo Găng tay 1 1 2 Máy I: 2 50 65 75 Máy II: 3 60 50 80
a) Hỏi phải phân công thời gian sản xuất của các máy như thế nào để trong một ngày
tạo ra được nhiều bộ đồ bảo hộ lao đồng nhất? Ước tính thời gian trung bình để
hoàn thành hợp đồng (2,5 điểm)
b) Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các máy như thế nào
để hoàn thành hợp đồng sớm nhất? (0.5 điểm)
Ở bài toán SXĐB: SV trình bày kết quả ở dạng số, lấy 2 chữ số thập phân sau dấu
phẩy; KHÔNG trình bày ở dạng phân số.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 1.2]: Sử dụng một số phương pháp để giải bài toán tối ưu hóa Câu 1
[CĐR 2.1]: Sử dụng thuật toán thế vị để giải bài toán vận tải Câu 2
[CĐR 3.1]: Sử dụng thuật toán nhân tử để giải bài toán sản xuất đồng bộ Câu 3
TP HCM, ngày …tháng…năm… Duyệt đề lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi cuối kỳ môn: Tối ưu hóa KHOA KINH TẾ Mã môn học: MAOP230706 BM QTKD Đề số: 1 Thời gian: 60 phút
Được phép sử dụng tài liệu
.Câu 1 (4 iểm) Cho bài toán gốc (P): (1) f(x) = 2x1 + 4x2 + 18x3 +2x4 max x1 + x2 + x3 +x4 ≥5 2x1 + 2x2 + x3 +x4 ≤ 10
3x1 + 2x2 + 2x3 +1x4 ≤10 x1 0 , x2 0 , x3 0, x4 0
a) Lập bài toán ối ngẫu (D) tương ứng của (P).
b) Giải bài toán (P). Suy ra kết quả bài toán (D)
Câu 2 (3 iểm) Một công ty có hai nhà máy A1, A2, với năng lực sản xuất trong thời gian
một tháng lần lượt là 80, 120 sản phẩm. Công ty có 3 cửa hàng phân phối sản phẩm l B1,
B2, B3 với nhu cầu sản phẩm tiêu thụ ở 3 cửa hàng lần lượt là 100, 60, 100 (sản
phẩm/tháng). Chi phí ể vận chuyển ể vận chuyển từ nhà máy ến cửa hàng ược cho ở bảng
sau ( v: nghìn ồng/ sản phẩm): Thu B 1 B 2 B 3 Phát 100 60 100 A 1 :80 5 6 7 A 2 :120 8 12 10
Ban giám ốc yêu cầu trạm B2 phải thu ủ hàng. Cấm tuyến ường A2 ến B1. Yêu cầu:
a. Hãy lập mô hình xác ịnh kế hoạch phân phối sao cho tổng chi phí vận chuyển là thấp nhất. (1 iểm)
b. Hỏi phải phân phối hàng từ nhà máy ến cửa hàng như thế nào ể chi phí vận chuyển
là thấp nhất? (2 iểm)
Câu 3: (3 iểm) Một xưởng gia công may mặc ký hợp ồng giao cho khách hàng 1000 bộ ồ
bảo hộ lao ộng (mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có 3 loại máy với năng suất
trung bình của mỗi máy khi sản xuất quần, áo, găng tay ược cho trong bảng sau (áo/ngày,
quần/ngày, găng tay/ngày) S.Ph ẩ m Qu ầ n Áo Găng tay lOMoAR cPSD| 58794847 1 1 2 Máy I: 2 30 40 100 Máy II: 1 30 80 120
a) Hãy lập mô hình bài tóan tối ưu sao cho tổng số bộ ồ lao ộng làm ra trong 1 ngày của
xưởng là nhiều nhất? (0.5 iểm)
b) Hỏi phải phân công thời gian sản xuất của các máy như thế nào ể tổng số bộ ồ lao
ộng làm ra trong 1 ngày của xưởng là nhiều nhất? Ước tính thời gian trung bình ể
hoàn thành hợp ồng? (2 iểm)
c) Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các máy như thế nào ể
hoàn thành hợp ồng sớm nhất? (0.5 iểm)
………………………………………………………………………………………………
Ghi chú : Cán bộ coi thi không ược giải thích ề thi. lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi cuối kỳ môn: Tối ưu hóa KHOA KINH TẾ Mã môn học: MAOP230706 BM QTKD Đề số: 2 Thời gian: 90 phút
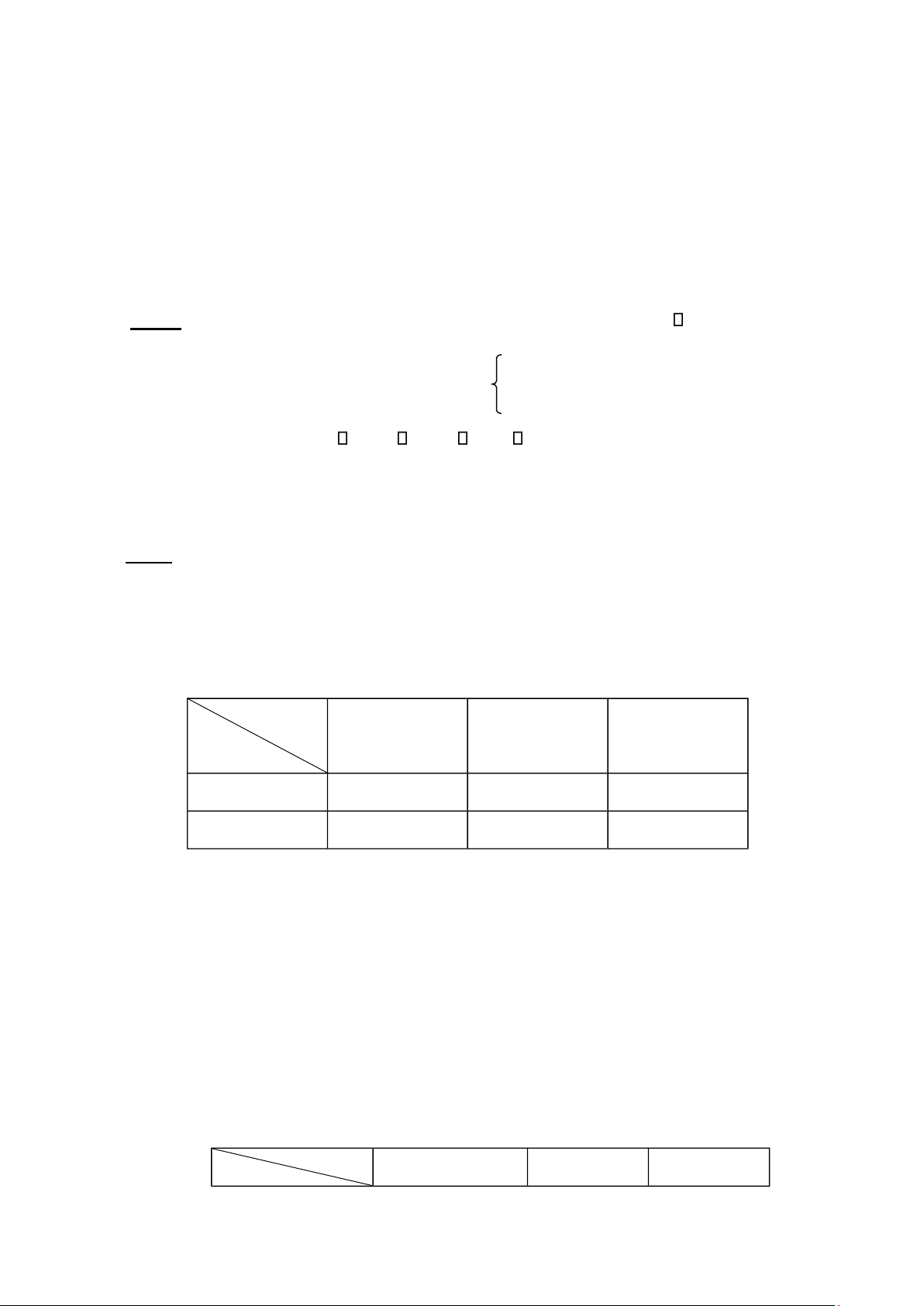
Được phép sử dụng tài liệu Câu 1 ( 3,5 iểm) Cho bài toán gốc (P):
(1) f(x) = 2x1 + 6x2 + 10x3 –x4 min
x x1 2 3x x3 4 8
2x2 x3 2x4 8 (2) 2 x1
x1 2x2 2x x3 4 12 (3) x1 0 , x2 0 , x3 0, x4 0
c) Lập bài toán ối ngẫu (D) tương ứng của (P). (1 iểm)
d) Giải 1 trong 2 bài toán rồi suy ra kết quả của bài toán còn lại. (2,5 iểm)
Câu 2 ( 3 iểm )
Một công ty sản xuất ra 1 loại hàng, có 3 nhà máy sản xuất ặt tại 3 ịa iểm khác nhau. Biết
công suất ở các nhà máy cho ở bảng sau: Nhà máy
Công suất (1000 sp/ tháng) A1 100 A2 120 A3 80
Sản phẩm của công ty ược phân phối ến 2 thị trường với mức tiêu thụ hàng tháng như sau: Thị trường
Khả năng tiêu thụ (1000 sp/ tháng) B1 90 B2 150 lOMoAR cPSD| 58794847
Biết lợi nhuận thu ược khi một nhà máy sản xuất ra 1 sản phẩm và phân phối ến thị trường
tương ứng như sau: ( ơn vị: 1.000 / sản phẩm) B1 B2 A1 12 11 A2 9 8 A3 11 6 Yêu cầu:
a. Hãy lập mô hình xác ịnh kế hoạch phân phối sao cho tổng lợi nhuận lớn nhất (1 iểm)
b. Hãy xác ịnh kế hoạch phân phối sao cho tổng lợi nhuận lớn nhất với iều kiện nhà máy
A1 phải sản xuất hết công suất. (2 iểm) Câu 3 : (3,5 iểm)
Một xưởng gia công may mặc ký hợp ồng giao cho khách hàng 6000 bộ ồ bảo hộ lao ông
(mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có 3 loại máy với năng suất trung bình của
mỗi máy khi sản xuất quần, áo, găng tay ược cho trong bảng sau (áo/ngày, quần/ngày, găng tay/ngày) S.Ph ẩ m Qu ầ n Áo Găng tay 1 1 2 Máy I: 2 100 140 240 Máy II: 1 40 180 280
d) Hãy lập mô hình toán tối ưu sao cho tổng số bộ ồ lao ộng làm ra trong 1 ngày của
xưởng là nhiều nhất? (1 iểm)
e) Hỏi phải phân công thời gian sản xuất của các máy như thế nào ể trong một ngày tạo
ra ược nhiều bộ ồ bảo hộ lao ồng nhất? Ước tính thời gian trung bình ể hoàn thành
hợp ồng (2 iểm)
f) Hỏi phải phân công trình tự sản xuất quần,áo, gắng tay của các máy như thế nào ể
hoàn thành hợp ồng sớm nhất? (0.5 iểm)
………………………………………………………………………………………………
Ghi chú: Cán bộ coi thi không ược giải thích ề thi. lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi môn: Tối ưu hóa KHOA KINH TẾ Môn học: MAOP230706 BM QTKD Đề số: 3 Thời gian: 60 phút
Được phép sử dụng tài liệu
Câu 1 (2 iểm)
Anh (chị) hãy lập mô hình toán học của bài toán sau ây (chỉ lập mô hình, không giải).
Một công ty sử dụng 4 loại nguyên liệu N1, N2, N3, N4 ể sản xuất ra 3 loại sản phẩm SP1, SP2,
SP3. Biết lợi nhuận của mỗi ơn vị sản phẩm (không phụ thuộc vào số giờ sản xuất và số sản
phẩm ược sản xuất), số lượng nguyên liệu hiện có, ịnh mức tiêu hao các loại nguyên liệu và
lượng sản phẩm làm ra trong một giờ ược cho trong bảng sau: Nguyên liệu
Số lượng nguyên Định mức tiêu hao nguyên liệu ( ơn vị) trong 1 liệu giờ hiện có SP1 SP2 SP3 N1 350 ( ơn vị) 2 3 4 N2 650 ( ơn vị) 6 8 9 N3 600 ( ơn vị) 3 5 7 N4 900 ( ơn vị) 8 10 9
Sản lượng (sản phẩm/giờ) 12 10 9
Lợi nhuận ( ồng/sản phẩm) 13.000 12.000 14.000
Sản phẩm của xí nghiệp sản xuất ra ều có thể tiêu thụ hết với iều kiện tiêu thụ là số sản phẩm
SP2 và SP3 phải có tỷ lệ 1:3. Hãy lập mô hình toán học tìm kế hoạch sản xuất sao cho lợi nhuận lớn nhất.
Câu 2 (4 iểm) Giải bài toán QHTT sau ay bằng phương pháp hình học:
f(x) = 3x1 +2x2 min (max) 3x1 2x2 2 3x1 2x2 2 D: 6x1 x24
2x1x 13 x20 , 2x 122 1
Câu 3: (4 iểm) Cho bài toán gốc (P): (1) f(x) = 3x1 +2x2 + 5x3 min
2x1 x2 2x3 8 (2) x1 x2 2x3 6
x1 2x2 x34 (3) x1 0, x2 0, x3 0
a) Lập bài toán ối ngẫu (D) tương ứng của (P). lOMoAR cPSD| 58794847
b) Dùng phương pháp ơn hình giải bài toán (P). Từ kết quả của (P) suy ra kết quả của bài toán (D)
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đề thi môn: Tối ưu hóa KHOA KINH TẾ Mã môn học: MAOP230706 BM QTKD Đề số 4 Thời gian: 60 phút
Được phép sử dụng tài liệu
Câu 1 (4 iểm) Cho bài toán gốc (P): f(x) = 3x1 + 4x2 + 4x3 min x1 + 2x2 + 2x3 ≤ 4 2x1 + x2 + 2x3 ≤ 5 3x1 + 4x2 + 2x3 = 6 x1 0 , x2 0 , x3 0
a) Lập bài toán ối ngẫu (D) tương ứng của (P).
b) Giải bài toán gốc (P). Từ kết quả của bài toán gốc (P), hãy suy ra PATƯ của bài toán ối ngẫu (D)
Câu 2 (3 iểm )
Một công ty sản xuất ra 1 loại hàng, có 2 nhà máy sản xuất ặt tại 2 ịa iểm khác nhau. Biết
công suất ở các nhà máy cho ở bảng sau: Nhà máy
Công suất (1000 sp/ tháng) A1 100 A2 180
Sản phẩm của công ty ược phân phối ến 3 cửa hàng với mức tiêu thụ hàng tháng như sau: Thị trường
Khả năng tiêu thụ (1000 sp/ tháng) B1 120 B2 110 B3 130
Biết lợi nhuận của 1 sản phẩm từ nhà máy ến thị trường tương ứng như sau: ( ơn vị: 1.000 / sản phẩm) lOMoAR cPSD| 58794847 B1 B2 B3 A1 12 14 12 A2 10 13 9 Yêu cầu:
Hãy xác ịnh kế hoạch phân phối sao cho tổng lợi nhuận lớn nhất với iều kiện cửa hàng B2 1 đ
phải nhận ủ hàng, và tuyến ường A1 ến B3 bị cấm.
Câu 3: (3 iểm)
Một xưởng gia công may mặc ký hợp ồng giao cho khách hàng 3000 bộ ồ bảo hộ lao ông(
mỗi bộ gồm 1 quần, 1 áo, 2 găng tay). Công ty có 2 loại máy với năng suất trung bình của
mỗi máy khi sản xuất quần, áo, găng tay ược cho trong bảng sau (áo/ngày, quần/ngày, găng tay/ngày) S.Ph ẩ m Qu ầ n Áo Găng tay 1 1 2 Máy I: 2 50 75 80 Máy II: 3 60 50 90 0.25đ
g) Hỏi phải phân công thời gian sản xuất của các máy như thế nào ể trong một ngày tạo
ra ược nhiều bộ ồ bảo hộ lao ồng nhất? Ước tính thời gian trung bình ể hoàn thành
hợp ồng (2,5 iểm)
h) Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các máy như thế nào ể
hoàn thành hợp ồng sớm nhất? (0.5 iểm)
Ở bài toán SXĐB: SV trình bày kết quả ở dạng số, lấy 2 chữ số thập phân sau dấu phẩy;
KHÔNG trình bày ở dạng phân số. 0.75đ ĐÁP ÁN ĐỀ SỐ 1 0.75đ Câu 1: a.Bài toán ối ngẫu: G(y) = 5y1 + 10y2 + 10y3 => MIN y1 + 2y2 + 3y3 >= 2 y1 + 2y2 + 2y3 >= 4 y1 + y2 + 2y3 >= 18 y1 + y2 + y3 >= 2
y1 <=0, y2 >=0, y3 >=0 b. Giải bài toán (P): lOMoAR cPSD| 58794847 Bài toán dạng chuẩn:
F(x) = 2x1 + 4x2 + 18x3 + 2x4 - Mx8 => MAX
x1 + x2 + x3 + x4 - x5 + x8 = 5 2x1 + 2x2 + x3 + x4 + x6 = 10 3x1 + 2x2 + 2x3 + x4 + x7 = 10
𝑥𝑗 ≥ 0 ∀ 𝑗 = 1,8̅̅̅̅ HSAC ACB PA X1 X2 X3 X4 X5 X6 X7 Lam B da 2 4 18 2 0 0 0 -M X8 5 1 1 1 1 -1 0 0 5 0 X6 10 2 2 1 1 0 1 0 10 0 X7 10 3 2 2 1 0 0 1 5 F(x) -5M -M-2 -M-4 -M-18 -M-2 M 0 0 18 X3 5 1 1 1 1 -1 0 0 - 0 X6 5 1 1 0 0 1 1 0 5 0 X7 0 1 0 0 -1 2 0 1 0 F(x) 90 16 14 0 16 -18 0 0 18 X3 5 3/2 1 1 1/2 0 0 1/2 - 0 X6 5 1/2 1 0 1/2 0 1 - - 1/2 0 X5 0 1/2 0 0 -1/2 1 0 1/2 - F(x) 90 25 14 0 7 0 0 9
Ta có ∆𝑖𝑗≥ 0∀ ô (𝑖, 𝑗) nên PA ang xét là PATƯ của bài toán dạng chuẩn:
x*=(0,0,5,0,0,5,0,0); F(x*) = 90
X8=0 với X8 là ẩn giả nên bài toán gốc ban ầu có PATƯ là: x*=(0,0,5,0); F(x*) = 90 Tìm
PATƯ của bài toán ối ngẫu (D):
X3*= 5 >0 → y1 + y2 + 2y3 = 18 (1) 0+ 0+ 5+0 = 5 → y1 < 0
2*0+ 2*0+ 5+0= 5<10→ y2 = 0 (2) 3*0+2*0+2*5+0=10→ y3 >0
Kết hợp (1), (2): y1 =18-2a; y2 =0; y3 =a với a>0 lOMoAR cPSD| 58794847
Hoặc y1 =a; y2 =0; y3 =(18-a)/2 với a<0
Kết luận: Y*=(18-2a, 0, a); (với a>0) ; G(y) = 90
Hoặc y*= (a,0,(18-a)/2) với a<0 ; G(y) = 90 Câu 2: a. Mô hình bài toán:
Gọi xij là lượng hàng vận chuyển từ nhà máy Ai ến cửa hàng Bj (i=1,2,3; j=1,2,3) Tìm xij sao cho:
0.75đ F(x)= 5*x11+6*x12+7*x13+M*x21+12*x22+ 10*x23+M*x32 →Min
x11+x12+x13 =80 x21+x22+x23 =120 x31+ x32 + x33 =60 x11 + x21
+x31 =100 x12+ x22 +x32=60 x13+x23+x33 =100 xij>=0, (i=1,2,3 ; j=1,2,3) b. Giải bài toán
𝐴1 + A2 = 200; B1 + B2 + B3 = 260 ⇒Thm trạm phát giả: A3=60.
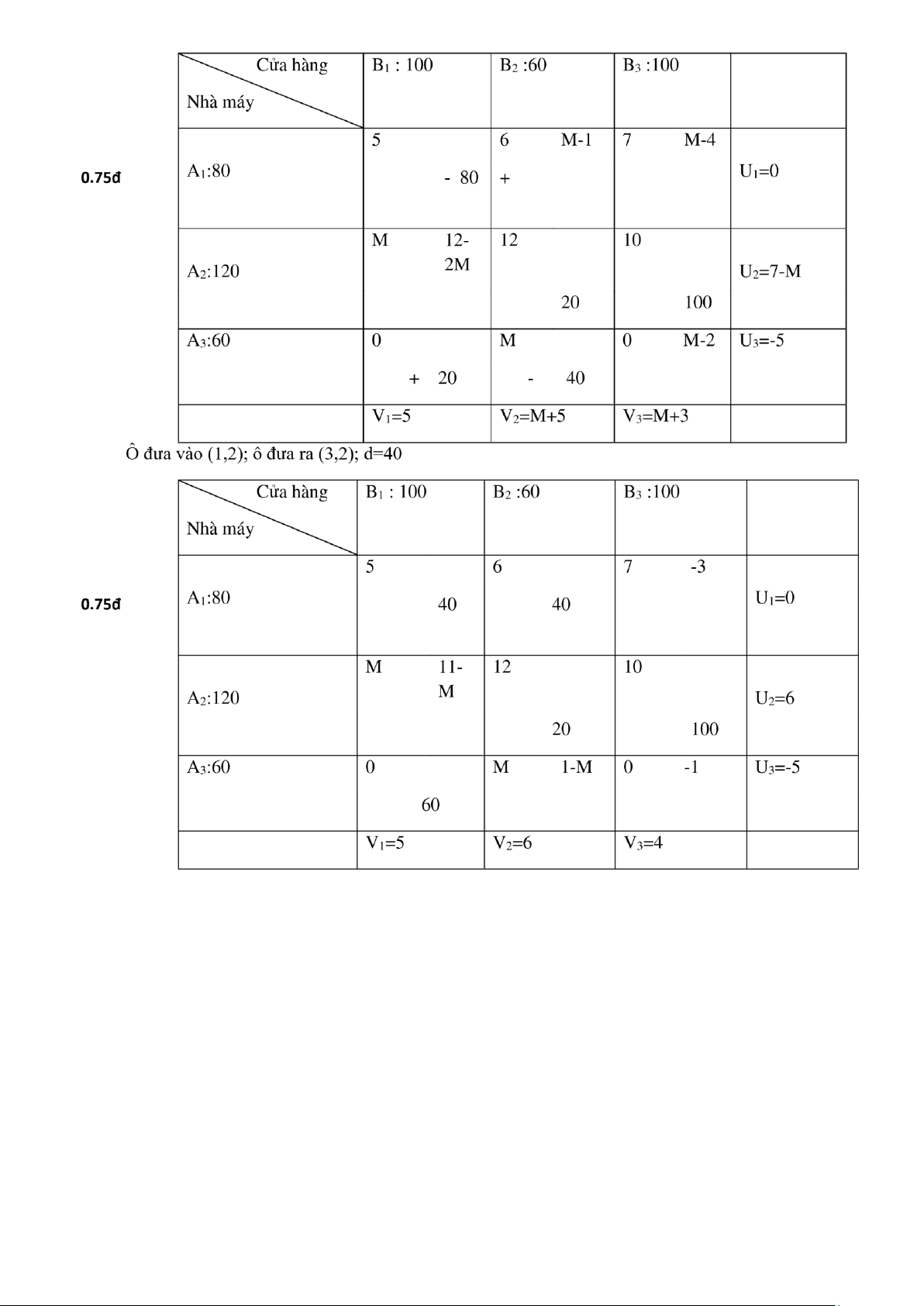
Do ban giám ốc yêu cầu trạm B2 phải thu ủ hàng. Cấm tuyến ường A2 ến B1 nên c32=M; c21=M (M>0, rất lớn) 1 đ 0.5đ lOMoAR cPSD| 58794847
Ta có ∆𝑖𝑗≤ 0∀ ô (𝑖, 𝑗) nên PA ang xét là PATƯ của bài toán VT (M): 40 40 0 𝑥∗ = ( 0 20 100) 60 0 0
X21=0, X32= 0 với ô (2,1); (3,2) l ô cấm nên bài toán VT ban ầu có PATƯ là: 40 40 0 𝑥∗ = ( 0
20 100) ; F(x)= 1.680.000 ( ồng) Câu 3: (4 iểm) a.Lập mô hình:
Gọi xij l phần thời gian trong 1 ngày phân công Mi sản xuất chi tiết Cj (xij ≥0) lOMoAR cPSD| 58794847
Các máy phải hoạt ộng liên tục trong suốt quỹ thời gian sản xuất. Do ó, iều kiện về thời
gian hoạt ộng của các máy là:
M1 : x11 + x12 +x13 =1 (giờ)
M2 : x21 + x22 +x23 =1 (giờ) 0. 5đ
Số sản phẩm các loại ược sản xuất trong 1 ngày:
Quần : z1 = 2*30*x11 +30*x21 Áo : z2 = 2*40*x12 +80*x22
Găng tay : z3 = 2*100/2*x13 +120/2*x23
Gọi z là số bộ ồ bảo hộ sản xuất ra trong 1 ngày z ≥ 0
Để tạo ra z bộ ồ bảo hộ thì số sản phẩm quần, áo, găng tay phải có ít nhất là z chi tiết : z ≤ z1 ; : z ≤ z2 ; z ≤ z3
Vấn ề ặt ra là: Tìm (xij) sao cho z cực ại? Mô hình bài toán: Tìm (xij) sao cho : z → max x11 + x12 +x13 =1 (ngày) x21 + x22 +x23 =1 (ngày) z ≤ 60*x11 +30*x21 z ≤ 80*x12 +80*x22 z ≤ 100*x13 +60*x23 z ≥0 ; xij ≥0 (i=1,2; j=1,2, 3) M/C C1: 1 C2: 1 C3: 1 U i M1: 1 60* 80* 100* 100 + M2: 1 30 80* 60 100 - Vj 1.67 + 1.25 - 1 + Z = = 51.06 1.67+1.25+1 0.75đ
Lập hệ phương trình và giải phương trình
Ta có X12 = -0.36 nên giả phương án này chưa phải là PATƯ → Ô ưa ra là ô (1,2) Lượng iều chỉnh: 1.67 Ô ưa ra: (1 ,2) Ô ưa vào: (2,3) lOMoAR cPSD| 58794847 M/C 0.75đ C1: 1 C2: 1 C3: 1 U i M1: 2 60* 80 100* 166.67 M2: 1 30 80* 60* 100 Vj 2.78 1.25 1.67 Z = 166,67+100 = 46.8̅̅̅̅3 2,78̅̅̅̅+1,25=1,67
Lập hệ phương trình và giải phương trình
Do mọi giá trị x ều >= 0 nên phương án tìm ược là tối ưu. M/C C1: 1 C2: 1 C3: 1 M1: 1 0.78 0 0.22 M2: 1 0 0.59 0.41
 Như vậy theo bảng trên nhà máy cần bố trí các máy làm việc trong một ngày như sau:
+ Bố trí máy M1 dành 0,78 thời gian sản xuất chi tiết C1 và 0,22 thời gian sản xuất chi tiết C3.
+ Bố trí máy M2 dành 0,59 thời gian sản xuất chi tiết C2 và 0,41 thời gian sản xuất chi tiết C3.
 Khi ó số lượng sản phẩm sản xuất ược là z = 46,83 Thời gian trung bình 0.5đ
ể hoàn thành hợp ồng là:
T= 1000/ 46,83 = 21.35 ngày (22 ngày)
Phân công trình tự sản xuất ể hoàn thành hợp ồng sớm nhất:
+ Bố trí máy M1 dành 0,78* 22= 17 thời gian sản xuất Quần trước và 0,22* 22= 5 thời gian
sản xuất Găng tay sau
+ Bố trí máy M2 dành 0,59* 22= 13 thời gian sản xuất Áo trước và 0,41 *22= 9 thời gian
sản xuất Găng tay sau 0.5đ lOMoAR cPSD| 58794847
ĐÁP ÁN ĐỀ SỐ 2 Câu 1: (3,5 iểm)
a. Bài toán ối ngẫu: G(y) = 8y1
+ 8y2 + 12y3 => MAX y1 + 2y2
+ y3 <= 2 y1 + 2y2 + 2y3 <= 6 -3y1 + y2 + 2y3 <= 10 1 đ y1 + 2y2 + y3 <= -1
y1 <=0, y2 ty ý, y3 <=0
b. Giải bài toán ơn giản hơn: giải bài toán (P) F(x) =
2x1 + 6x2 + 10x3 - x4 + Mx7 => MIN 0. 25đ x1 + x2 -3x3 + x4 + x5 = 8 2x1 + 2x2 + x3 + 2x4 + x7 = 8 x1 + 2x2 + 2x3 + x4 + x6 = 12
x1 >=0, x2 >=0, x3 >=0, x4 >=0, x5 >=0, x6 >=0, x7 >=0 C X X X X X Lamda 0. 5đ i Xi Yi X1 2 3 4 5 6 2 6 10 -1 0 0 0 X5 8 1 1 -3 1 1 0 8 M X7 8 2 2 1 2 0 0 4 0 X6 12 1 2 2 1 0 1 12 8M 2M-2 2M-6 M-10 2M+1 0 0 Ci Xi Yi X1 X2 X3 X4 X5 X6 Lamda 0. 5đ 0 X5 4 0 0 -7/2 0 1 0 - -1 X4 4 1 1 1/2 1 0 0 - 0 X6 8 0 1 3/2 0 0 1 - lOMoAR cPSD| 58794847 F(x) -4 -3 -7 -21/2 0 0 0
Ta có ∆𝑗≤ 0∀ 𝑗 nên PA ang xét là PATƯ của bài toán dạng chuẩn : x*=(0,0,0,4,4,8,0); F(x*) = -4
0. 25đ X7=0 với X7 là ẩn giả nên bài toán gốc ban ầu có PATƯ là: x*=(0,0,0,4); F(x*) = -4
Tìm PATƯ của bài toán ối ngẫu (D): x4 = 1đ
4 >0 => y1 + 2y2 + y3 = -1 (1) Thay X*
vào các ràng buộc ta có:
x1 + x2 -3x3 + x4 = 4 < 8 => y1 = 0 (2) x1
+ 2x2 + 2x3 + x4 = 4 < 12 => y3 = 0 (3) Từ (1), (2) và (3) ta có: Y* = (0,-1/2, 0) G(Y*) = -4 Câu 2: (3 iểm) c. Mô hình bài toán:
Tổng hàng phát ra = 300 > tổng thu = 240, ặt trạm thu giả B3=60 1 đ
Gọi xij là lượng hàng vận chuyển từ nhà máy Ai ến cửa hàng Bj (i=1,2,3; j=1,2,3) Tìm xij sao cho:
F(x)= 12*x11+11*x12+ 9*x21+8*x22+11*x31+6*x32 →Max
x11+x12+x13 =100 x21+x22+x23 =120 x31+x32+x33 =80
x11+x21+x31 =90 x12+x22+x32 =150 x13+x23+x33 =60 xij>=0, (i=1,2,3; j=1,2,3)
(Hoặc Sv có thể không thêm trạm thu giả thì dấu<= ở ràng buộc 1,2,3 thì vẫn ược trọn iểm) d. Giải bài toán
𝐴1 + A2 + A3 = 300; B1 + B2 = 240 ⇒Thêm trạm phát giả: B3=60. 0.25đ
Do ban giám ốc yêu cầu A1 phải sản xuất hết công suất nên c13= - M (M>0, rất lớn)