Đề thi HK1 lớp 10 ban cơ bản trường Chu Văn An – Hà Nội 2014 – 2015

Giới thiệu đến thầy, cô và các em học sinh Đề thi HK1 lớp 10 ban cơ bản trường Chu Văn An – Hà Nội năm học 2014 – 2015 có lời giải và thang điểm, mời bạn đọc đón xem

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

4 trang 7 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT CHU VĂN AN
ĐỀ SỐ 1
ĐỀ THI HỌC KÌ I NĂM HỌC 2013-2014
Môn: Toán lớp 10 (Khối A)
Dành cho các lớp A, Toán, Lý, Hóa, Sinh, Tin
Thời gian là bài: 120 phút, không kể thời gian phát đề
_____________________________________
Câu 1 (3,0 điểm). Cho hàm số
2
2 3.y x x
1. Khảo sát sự biến thiên và vẽ đồ thị
P
của hàm số trên.
2. Tìm
m
để đường thẳng
y x m
cắt đồ thị
P
tại hai điểm
,AB
sao cho
Câu 2 (2,0 điểm). Giải các phương trình sau
1.
2
3 3 3 1;x x x
2.
22
3 5 7 3 .x x x x
Câu 3 (1,0 điểm). Giải hệ phương trình
2
2
2 1 0
5 2 12 11 0.
y x y
y x y
Câu 4 (2,0 điểm). Trong mặt phẳng tọa độ
,Oxy
cho các điểm
2; 1 ,A
4; 3 .B
1. Tìm tọa độ điểm
C
sao cho tam giác
ABC
vuông cân tại
.A
Tính diện tích của
tam giác
.ABC
2. Tìm tọa độ điểm
M
trên trục
Oy
sao cho
2 . 8,AM OM BM
(điểm
O
là gốc tọa
độ).
Câu 5 (1,5 điểm). Cho hình bình hành
ABCD
có hai cạnh
10, 5,AB AD
góc
0
120 .BAD
Trên cạnh
CD
lấy điểm
E
sao cho
4.DE
1. Tính
.AB AD
và biểu diễn véc tơ
AE
theo hai véc tơ
,.AB AD
2. Chứng minh
.BD AE
Câu 6 (0,5 điểm). Tìm các giá trị của
m
để phương trình
2
44x x m x x
có
nghiệm.
--------------------HẾT------------------------
Thí sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
Họ và tên:…………………………….Số báo danh:………………
ĐÁP ÁN ĐỀ THI HỌC KÌ I MÔN TOÁN LỚP 10– NĂM HỌC 2013-2014
BAN A – ĐỀ SỐ 1
(Gồm 2 trang)
Câu
Sơ lược đáp án
Điể
m
Tổng số
1
1
+) Khảo sát sự biến thiên của hàm số
2
23xyx
TXĐ:
0.25
2,0 điểm
Bảng biến thiên
1 0; 1
2
b
a
a
0.50
Kết luận: Hàm số nghịch biến trên khoảng
1; ,
đồng
biến trên khoảng
;1 .
0.25
+) Đồ thị:
Xác định tọa độ đỉnh (P), giao trục tung, giao trục hoành.
0,50
Vẽ đúng đồ thị (có tọa độ các điểm đã xác định)
Kết luận: Đồ thị là parabol có truc đối xứng là đường thẳng
1x
( * Nếu không kết luận châm trước không trừ điểm)
0,50
2
Xét phương trình hoành độ giao điểm:
2
23xx xm
2
3 0, 1xmx
P
cắt đường thẳng
y x m
tại hai điểm
,AB
13
0
4
m
0.25
1 điểm
Gọi
AB
; , ;
AB
A x x m B x x m
1, 3
A B A B
x x x x m
0.25
2
AB
22
2 2 4 2 13 4
A B A B A B
x x x x x x m


0.25
10 2 13 4 10 2AB m m
0.25
2
1
22
3 3 3 1 3 3 1 3 , 1x x x x x x
Điều kiện có nghiệm:
1
1 3 0
3
xx
0.25
1
,
3
x
22
22
2
3 3 1 3 4
1 3 11
3 3 3 1 6 2 0
3 11
x
x x x x
x
x x x x x
x






0.50
Kết hợp với
1
,
3
x
nghiệm của pt
1
là
2; 3 11xx
0.25
2
22
2 3 5 3 5 12 0x x x x
0.25
1 diểm
2
3 5 4x x a
hoặc
2
3 5 3x x b
0.25
a
vô nghiệm,
1; 4b x x
0.50
3
2
2
21
10 9 0
x y y
hpt
yy
0.25
1 điểm
2
21
1
x y y
y

hoặc
2
21
9
x y y
y

0.50
2
1
x
y


hoặc
0,25
4
1
Gọi
; 2; 1 , 2; 2C x y AC x y AB
1 điểm
2 2 2 1 0 3, 1AC AB x y x y
0.25
22
2 1 8, 2AC AB x y
0.25
0
1 , 2
3
x
y

hoặc
4
0; 3
1
x
C
y

hoặc
4;1C
0.25
Diện tích tam giác
ABC
là
2
1
4
2
AB
(đvdt)
0.25
2
0; 2 2;3 1 , 4; 3M Oy M y AM OM y BM y
0.50
1 điểm
2 . 8 8 1 3 3 8AM OM BM y y
0.25
3y
hoặc
1
3
y
0; 3M
hoặc
1
0;
3
M



0.25
5
1
0
. . .cos120 25;AB AD AB AD
0.25
0,5 điểm
2
5
AE AD DE AD AB
0.25
2
.0BD AE BD AE BD AE
0.25
1 điểm
2
.0
5
AD AB AD AB



0.25
22
22
. . 0
55
AD AB AD AB AD AB
0.25
00
Đúng
0.25
6
ĐK:
22
0;4 . 4 2 4 4x PT x x x x m
0,5 điểm
Đặt
2
4,t x x
điều kiện
0;2t
0.25
PT ban đầu có nghiệm
2
24PT t t m
có nghiệm
0;2t
Lập bảng biến thiên suy ra
4;5m
0.25
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI HỌC KÌ I NĂM HỌC 2013-2014
TRƯỜNG THPT CHU VĂN AN
Môn: Toán lớp 10 (Khối A)
Dành cho các lớp A, Toán, Lý, Hóa, Sinh, Tin ĐỀ SỐ 1
Thời gian là bài: 120 phút, không kể thời gian phát đề
_____________________________________
Câu 1 (3,0 điểm). Cho hàm số 2
y  x  2x  3.
1. Khảo sát sự biến thiên và vẽ đồ thị  P của hàm số trên.
2. Tìm m để đường thẳng y x m cắt đồ thị  P tại hai điểm , A B sao cho AB  10.
Câu 2 (2,0 điểm). Giải các phương trình sau 1. 2
x  3x  3  3x  1; 2. 2 2
x x  3x  5  7  3 . x
Câu 3 (1,0 điểm). Giải hệ phương trình 2
2y x y 1 0  2 5
 y  2x 12y 11 0.
Câu 4 (2,0 điểm). Trong mặt phẳng tọa độ Oxy, cho các điểm A2;  1 , B 4; 3  .
1. Tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại .
A Tính diện tích của tam giác ABC.
2. Tìm tọa độ điểm M trên trục Oy sao cho  AM  2OM .BM  8, (điểm O là gốc tọa độ).
Câu 5 (1,5 điểm). Cho hình bình hành ABCD có hai cạnh AB 10, AD  5, góc 0
BAD  120 . Trên cạnh CD lấy điểm E sao cho DE  4. 1. Tính A .
B AD và biểu diễn véc tơ AE theo hai véc tơ A , B A . D
2. Chứng minh BD A . E
Câu 6 (0,5 điểm). Tìm các giá trị của m để phương trình 2
x  4  x m  4x x có nghiệm.
--------------------HẾT------------------------
Thí sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
Họ và tên:…………………………….Số báo danh:………………
ĐÁP ÁN ĐỀ THI HỌC KÌ I MÔN TOÁN LỚP 10– NĂM HỌC 2013-2014 BAN A – ĐỀ SỐ 1 (Gồm 2 trang) Câu Sơ lược đáp án Điể Tổng số m
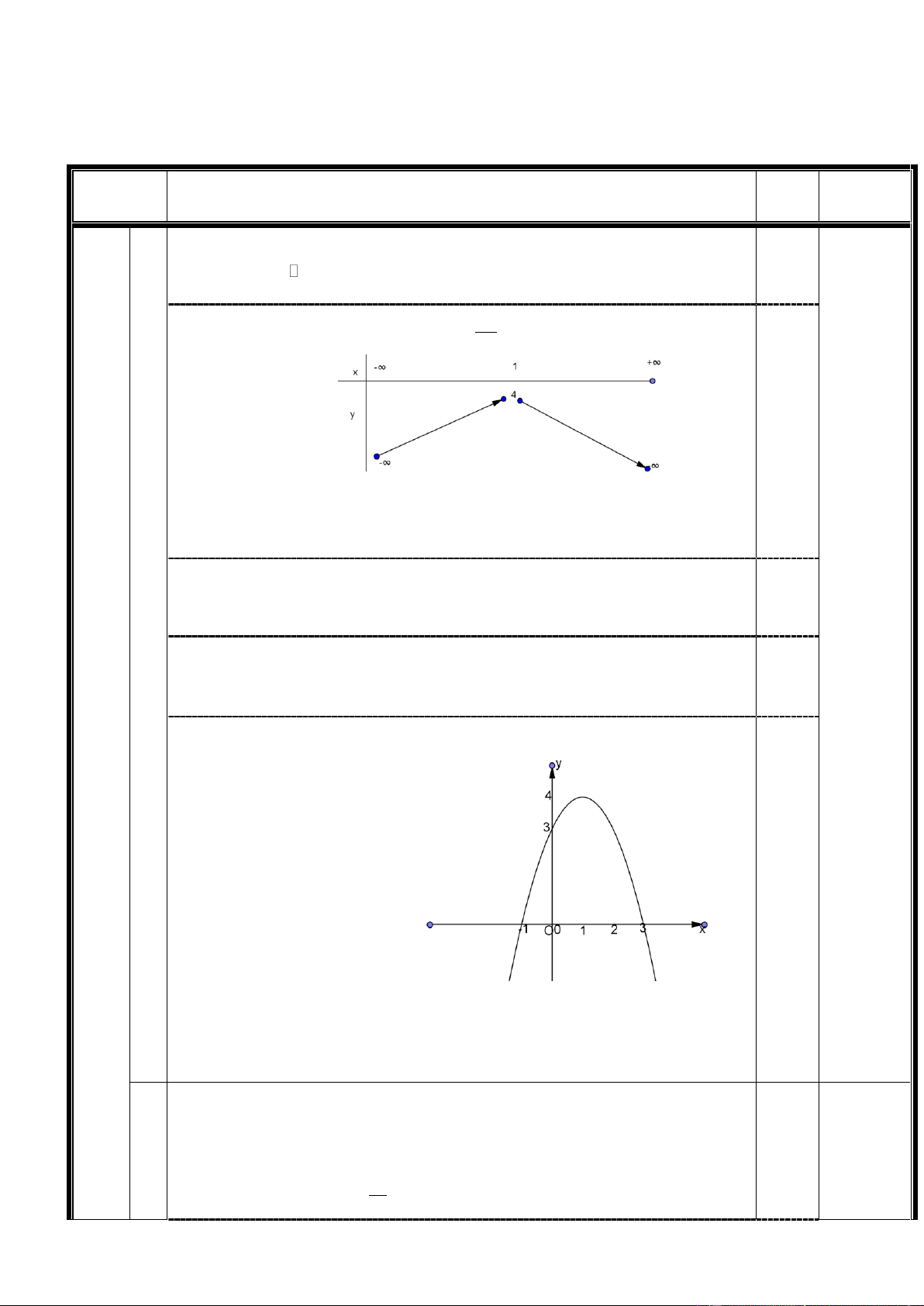
1 +) Khảo sát sự biến thiên của hàm số 2
y  x  2x  3  TXĐ: 0.25 b      Bảng biến thiên a 1 0; 1 2,0 điểm 2a 0.50 1
 Kết luận: Hàm số nghịch biến trên khoảng 1;, đồng biến trên khoảng  0.25 ;   1 . +) Đồ thị:
 Xác định tọa độ đỉnh (P), giao trục tung, giao trục hoành. 0,50 0,50
Vẽ đúng đồ thị (có tọa độ các điểm đã xác định)
Kết luận: Đồ thị là parabol có truc đối xứng là đường thẳng x 1
( * Nếu không kết luận châm trước không trừ điểm) 2
Xét phương trình hoành độ giao điểm: 1 điểm  2
x  2x  3  x m 2
x x m  3  0,  1 
P  cắt đường thẳng y x m tại hai điểm 0.25 , A B  13   0  m  4
 Gọi Ax ;x m ,B x ;x m x x 1, x x m 3 0.25 A A   B B  A B A B  2 2 2
AB  2 x x   2 
x x  4x x   2134m A B A B A B    0.25
AB  10  2134m 10  m  2 0.25 2 1 2 2
x  3x  3  3x  1  x  3x  3  1 3x,   1 0.25 1
 Điều kiện có nghiệm: 13x  0  x  3 x  2  0.50 2 2 
  x 3x 3 13x x  4         1 x  , 1 x 3 11  3 2 2
x 3x 3  3x 1
x  6x  2  0  x  3  11   Kết hợp với 1 0.25 x  , nghiệm của pt   1 là     x 2; x 3 11 3 2    2 2 1 diểm
2  x  3x  5  x  3x  5 12  0 0.25  2
x  3x  5  4  a hoặc 2
x  3x  5  3b 0.25     
a vô nghiệm, bx 1; x 4 0.50 3 2  x  2  y y 1 0.25 1 điểm hpt   2
y 10y  9  0 2 2 
x  2y y 1 x  2  y y 1 0.50   hoặc  y  1  y  9   x  2  x   0,25   hoặc 154  y  1   y  9 4 1
 Gọi C ;x y  ACx 2; y   1 , AB 2; 2   1 điểm
AC AB  2 x  2  2 y  
1  0  x y  3,  1 0.25
AC AB  x  2   y  2 2 1  8,2 0.25  x  x  4 0.25     0 1 , 2   hoặc   C 0; 3
  hoặc C 4;  1 y  3   y  1  1 Diện tích tam giác 0.25 ABC là 2 AB  4 (đvdt) 2 2
M Oy M 0; y  AM  2OM   2  ;3y   1 , BM  4  ; y  3 0.50 1 điểm
 AM 2OM .BM 8 813y3 y 8 0.25    0.25 y  3  hoặc 1 y    M 0; 3   hoặc 1 M 0;    3  3  5 1  0 A . B AD A . B A . D cos120  2  5;
0.25 0,5 điểm  2 0.25
AE AD DE AD AB 5 2
BD AE BD AE B . D AE  0 0.25 1 điểm    0.25
  AD AB 2 . AD AB  0    5   2 2   0.25 AD 2 2  A . B AD A . B AD  AB 0 5 5   0  0 Đúng 0.25 6  ĐK: x  2 2 0; 4 .
PT  4x x  2 4x x  4  m 0,5 điểm Đặt 2
t  4x x , điều kiện t 0; 2 0.25
 PT ban đầu có nghiệm 2
PT t  2t  4  m có nghiệm t 0; 2
Lập bảng biến thiên suy ra m4;5 0.25