Đề thi HK1 Toán 10 năm 2019 – 2020 trường Lương Thế Vinh – Hà Nội

Đề thi HK1 Toán 10 năm học 2019 – 2020 trường THCS&THPT Lương Thế Vinh – Hà Nội mã đề 281 gồm 06 trang với 50 câu trắc nghiệm, thời gian làm bài 90 phút, mời các bạn đón xem

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

26 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 1
ĐỀ THI HỌC KÌ I NĂM HỌC 2019 - 2020
Môn thi: TOÁN - Khối: 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
----------------------------
Câu 1: Số các giá trị nguyên của
m
để phương trình
2
30x x m− − =
có bốn nghiệm phân biệt là
A. vô số. B.
0
. C.
2
. D.
4
.
Câu 2: Cho parabol
( )
2
:4P y ax bx= + +
đi qua điểm
( )
1;7A
và có trục đối xứng
1x =−
. Tích
ab
nhận
giá trị bằng
A.
. B.
4
. C.
18−
. D.
2
.
Câu 3: Nghiệm của hệ phương trình
22
2 3 10
xy
xy
− = −
+=
là
A.
( ) ( )
; 2;2xy=
. B.
( ) ( )
; 3;6xy=
. C.
( ) ( )
; 2; 2xy= − −
. D.
( ) ( )
; 1; 2xy=−
.
Câu 4: Cho đoạn thẳng
6AB =
. Tập hợp các điểm
M
thỏa mãn
22
18MA MB+=
là
A. một đoạn thẳng. B. một điểm. C. một đường tròn. D. một đường thẳng.
Câu 5: Trong mặt phẳng tọa độ
Oxy
,
cho tam giác
ABC
vuông tại
( )
2;2A
. Biết
( )
4; 2C −
và
B Oy
. Tìm
tọa độ điểm
B
.
A.
( )
0;3B
. B.
( )
0; 3B −
. C.
( )
0;1B
. D.
( )
0; 1 .B −
Câu 6: Lớp
10D
có
37
học sinh, trong đó có
17
học sinh thích môn Văn,
19
học sinh thích môn Toán,
9
em không thích môn nào. Số học sinh thích cả hai môn là
A.
2
học sinh. B.
6
học sinh. C.
13
học sinh. D.
8
học sinh.
Câu 7: Phương trình
4
4
22
x
x
xx
−
−
=
−−
có tất cả bao nhiêu nghiệm nguyên?
A.
1
. B. Vô số. C.
2
. D.
0
.
Câu 8: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
2yx=−
cắt parabol
( )
2
:2P y x mx= − +
tại đúng một điểm.
A.
3
5
m
m
=
=−
. B.
3m =
. C.
5m =−
. D.
m
.
Câu 9: Cho các vectơ
a
,
b
có độ dài bằng
1
và
3 4 13ab−=
. Tính
( )
cos ,ab
.
A.
1
2
. B.
1
. C.
1
4
. D.
3
2
.
Câu 10: Cho tam giác
ABC
nhọn có
3BC a=
và bán kính đường tròn ngoại tiếp tam giác
ABC
là
3Ra=
.
Tính số đo góc
A
.
TRƯỜNG LƯƠNG THẾ VINH - HÀ NỘI
--------------------------------------
MÃ ĐỀ THI: 281
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 2
A.
120=A
. B.
45=A
. C.
30=A
. D.
60=A
.
Câu 11: Số nghiệm của hệ phương trình
22
5
5
xy x y
xy
+ + =
+=
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 12: Cho tam giác
ABC
là tam giác đều,
O
là tâm đường tròn ngoại tiếp tam giác
ABC
. Tìm mệnh đề
đúng trong các mệnh đề sau.
A.
OA OB OC+=
. B.
2OA OB OC+=
. C.
OA OB CO+=
. D.
2OA OB CO+=
.
Câu 13: Cho Parabol
( )
2
:2P y x bx c= − + +
có điểm
( )
2;10M
là điểm có tung độ lớn nhất. Tính giá trị của
c
.
A.
22
. B.
6.
C.
12.
D.
10.
Câu 14: Trong các hàm số sau đâu là hàm số bậc nhất?
A.
( )( )
2
1 1 2 .y x x x x= − + + +
B.
( )
2
1
2 1 .yx
x
= − −
C.
2
1.yx=−
D.
62
.
x
y
x
+
=
Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.
:3 3
n
nn +
. B.
1 2 6 7
.
C.
6 4 10 7
. D.
( )
2
2
:2x x x −
.
Câu 16: Số nghiệm của phương trình
( )
2
3 9 20 0x x x− − + =
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 17: Cho ba điểm bất kỳ
,,M N P
. Đẳng thức nào sau đây sai?
A.
PM NM NP=−
. B.
MN NP PM+ = −
. C.
MN MP PN=−
. D.
NP MP NM=+
.
Câu 18: Trong mặt phẳng tọa độ
Oxy
, cho
( ) ( )
1;3 ; 1; 8AB−−
. Tìm điều kiện của
a
để điểm
( )
;0Ma
thỏa
mãn góc
AMB
là một góc tù.
A.
5;5a−
. B.
( )
5;a +
. C.
( )
;5a − −
. D.
( )
5
5;5 \ .
11
a

−


Câu 19: Một học sinh giải phương trình
( )
2
2 4 2x x *+=
như sau:
Bước 1: Điều kiện xác định là
¡
.
Bước 2:
( )
22
2 4 4* x xÛ + =
Bước 3:
2
2xÛ=
. Vậy phương trình có nghiệm
2x=
và
2x =-
Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào?
A. Lời giải đúng. B. Lời giải sai từ bước 1.
C. Lời giải sai từ bước 2. D. Lời giải sai từ bước 3.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 3
Câu 20: Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng?
A.
3
3y x x=+
. B.
33y x x= + + −
. C.
( )
2
1yx=+
. D.
1x
y
x
−
=
.
Câu 21: Phương trình
22
7 6 2 4x x x x− + = − +
có bao nhiêu nghiệm nguyên âm?
A. 2. B. 0. C. 1. D. 3.
Câu 22: Có bao nhiêu giá trị của tham số
m
để hai đường thẳng
( )
1
: 1 3 2d y m x m= − + −
và
( )
2
2
: 1 2 1d y m x m= − + −
song song với nhau?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 23: Cho tam giác
ABC
có
4cmAB =
;
12cmAC =
và góc
120BAC =
. Tính diện tích tam giác
ABC
.
A.
12 3
(
2
cm
). B.
24 3
(
2
cm
). C.
12
(
2
cm
). D.
24
(
2
cm
).
Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của a?
A.
3aa
. B.
22
2aa−
. C.
23aa− −
. D.
1
3
aa−
.
Câu 25: Cho tam giác
ABC
thỏa mãn
2 2 2
2 . 0BC AC AB BC AC+ − − =
. Khi đó, góc
C
có số đo là
A.
150C =
. B.
60C =
. C.
45C =
. D.
30C =
.
Câu 26: Cho hình bình hành
ABCD
có
1, 2, 60AB AD DAB= = =
. Tính độ dài cạnh
AC
.
A.
3
. B.
7
3
. C.
7
. D.
5
.
Câu 27: Cho hàm số
2
( 0)y ax bx c a= + +
có bảng biến thiên như hình vẽ dưới đây
Xác định dấu của
,,abc
A.
0, 0, 0abc
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
D.
0, 0, 0a b c
.
Câu 28: Cho hàm số
2
( ) 4 2y f x x x= = − +
trong các mệnh đề dưới đây mệnh đề nào đúng?
A.
( ) ( )
2019 2019
23ff− −
.
B.
( ) ( )
2019 2019
23ff
.
C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
D. Đồ thị hàm số nhận đường thẳng
2x =−
làm trục đối xứng.
Câu 29: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
5;3 , 2; 1 , 1;5A B C−−
. Tìm tọa độ điểm
H
là trực tâm tam giác
ABC
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 4
A.
( )
3;2H
. B.
( )
3; 2H −
. C.
7
2;
3
H



. D.
7
2;
3
H

−−


.
Câu 30: Cho
,ab
là hai số thực tùy ý. Mệnh đề nào sau đây đúng?
A. Nếu
22
ab
thì
ab
. B. Nếu
ab
thì
22
ab
.
C. Nếu
ab
và
0a
thì
22
ab
. D. Nếu
ab
và
0b
thì
22
ab
.
Câu 31: Tổng các nghiệm của phương trình
( ) ( )
42
3 2 4 3 2 0xx− − − − =
là
A.
1−
. B.
4
32−
. C.
0
. D.
2
32−
.
Câu 32: Trong mặt phẳng tọa độ
Oxy
, cho hình bình hành
ABCD
có
( )
1;2A
,
( )
2;4B −
,
( )
0;3C
. Tìm tọa
độ điểm
D
.
A.
( )
3;1−
. B.
( )
3;1
. C.
( )
3; 1−
. D.
( )
3; 1−−
.
Câu 33: Giá trị lớn nhất của hàm số
2
3 2 5y x x= − + +
trên
2
;1
3

−


là
A.
16
3
. B.
5
. C.
1
. D.
7
3
.
Câu 34: Cho tam giác
ABC
có
..AB BC BC AC=−
. Tam giác
ABC
có tính chất gì?
A.
ABC
vuông tại
A
. B.
ABC
cân tại
B
.
C.
ABC
vuông tại
B
. D.
ABC
cân tại
A
.
Câu 35: Cho tam giác
ABC
có
10AB =
,
17AC =
,
15BC =
. Tính
.AB AC
uuur uuur
.
A.
164
. B.
164−
. C.
82−
. D.
82
.
Câu 36: Tập xác định của hàm số
2
42
12
xx
y
xx
− + +
=
−−
là
A.
2;4−
. B.
( ) ( )
3; 2 2;4− − −
. C.
( )
2;4−
. D.
)
2;4−
.
Câu 37: Tìm giá trị của tham số
m
để đỉnh
I
của đồ thị hàm số
2
6y x x m= − + +
thuộc đường thẳng
2019yx=+
.
A.
2020m =
. B.
2000m =
. C.
2036m =
. D.
2013m =
.
Câu 38: Cho tam giác
ABC
vuông cân tại
A
có
2BC a=
. Tính độ dài
BA BC+
.
A.
25a
. B.
5a
. C.
3a
. D.
23a
.
Câu 39: Biết đường thẳng
:4d y x= − +
cắt parabol
( )
2
:2P y x x=−
tại hai điểm phân biệt
A
và
B
. Tìm tọa
độ trọng tâm
G
của tam giác
OAB
.
A.
17
;
33
G



. B.
( )
1; 2G −
.
C.
1 17 9 17
;
33
G

−−



. D.
17
;
22
G



.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 5
Câu 40:
Cho hệ phương trình
21
2 2 1
mx y m
x my m
+ = +
+ = −
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hệ
phương trình đã cho vô nghiệm.
A.
2.m =−
B.
2.m −
C.
2.m
D.
2.m =
Câu 41: Giá trị nhỏ nhất của hàm số
6
()
22
x
fx
x
=+
−
với
2x
là số có dạng
3ab+
(
,ab
là các số nguyên).
Tính
22
.ab+
A.
5.
B.
6.
C.
3.
D.
4.
Câu 42: Số các giá trị thực của tham số
m
để phương trình
( )( )
21
0
1
x mx
x
−+
=
+
có nghiệm duy nhất là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 43: Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
21x x m− + =
có hai nghiệm phân biệt.
A.
0m
. B.
0m
. C.
1m
hoặc
0m =
. D.
01m
.
Câu 44: Tìm tất cả các giá trị thực của tham số
m
để phương trình
32
0x mx x m− − + =
có ba nghiệm thực
phân biệt.
A.
1m −
. B.
1m 
. C.
1m
hoặc
0m =
. D.
01m
.
Câu 45: Cho phương trình
2
10x mx m− + + + =
với
m
là tham số thực. Tính tổng
S
tất cả các giá trị thực
của tham số
m
để phương trình có hai nghiệm phân biệt
12
,xx
thỏa mãn
12
4xx+=
.
A.
2S =
B.
2S =−
. C.
4S =−
D.
5S =
.
Câu 46: Cho phương trình
2
10 2x x m x− + = −
. Tìm tất cả các giá trị thực của tham số
m
để phương trình
đã cho vô nghiệm.
A.
16 20m
. B.
3 16m−
C.
m
. D.
16m
.
Câu 47: Tập tất cả các giá trị của tham số
m
để phương trình
22
1x x m+ − =
có tập nghiệm là
;ab
. Tính
S a b=+
?
A.
0.
B.
9
.
4
C.
1.
D.
1
.
4
Câu 48: Cho hàm số
2
2y x x=−
có đồ thị như hình vẽ. Gọi
S
là tập các giá trị nguyên của
m
đề phương
trình
2
21x x m− + =
có hai nghiệm phân biệt. Tính tổng các phần tử của tập
S
.
A.
1−
. B.
2
. C.
4
. D.
0
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 6
Câu 49: Trong hệ tọa độ
Oxy
cho ba điểm
( )
1; 4A −
,
( )
4;5B
và
( )
0; 9C −
. Điểm
M
di chuyển trên trục
Ox
. Đặt
2 2 3Q MA MB MB MC= + + +
. Biết giá trị nhỏ nhất của
Q
có dạng
ab
trong đó
a
,
b
là
các số nguyên dương và
a
,
20b
. Tính
ab−
.
A.
15−
. B.
17−
. C.
14−
. D.
11−
.
Câu 50: Cho
,xy
thoả mãn
22
x y a+=
. Xác định
a
, biết rằng giá trị lớn nhất của
23P x y=+
với
,0xy
là
117
.
A.
9a =
. B.
13a =
. C.
5a =
. D.
33a =
.
---------- HẾT ----------
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 7
BẢNG ĐÁP ÁN
1.C
2.D
3.A
4.B
5.C
6.D
7.C
8.A
9.A
10.D
11.A
12.C
13.B
14.A
15.D
16.B
17.C
18.D
19.C
20.B
21.B
22.C
23.A
24.C
25.C
26.C
27.B
28.B
29.A
30.C
31.C
32.B
33.A
34.D
35.D
36.D
37.D
38.B
39.A
40.A
41.A
42.A
43.C
44.B
45.B
46.D
47.B
48.B
49.D
50.A
GIẢI CHI TIẾT ĐỀ HỌC KỲ I LỚP 10 MÔN TOÁN
THPT LƯƠNG THẾ VINH-HÀ NỘI
NĂM HỌC 2019 - 2020
Câu 1. Số các giá trị nguyên của
m
để phương trình
2
30x x m− − =
có bốn nghiệm phân biệt là
A. vô số. B.
0
. C.
2
. D.
4
.
Lời giải.
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai
Chọn C
22
3 0 3x x m x x m− − = − =
(*)
Xét hàm số
( )
2
3f x x x=−
, ta có bảng biến thiên của hàm số
( )
y f x=
như sau:
Từ đó ta suy ra bảng biến thiên của hàm số
( )
y f x=
như sau:
Yêu cầu bài toán
phương trình (*) có 4 nghiệm phân biệt
đường thẳng
ym=
cắt đồ thị hàm số
( )
y f x=
tại 4 điểm phân biệt
9
0
4
m
(dựa vào BBT của hàm số
( )
y f x=
).
Do
m
nên
1;2m
.
Câu 2. Cho parabol
( )
2
:4P y ax bx= + +
đi qua điểm
( )
1;7A
và có trục đối xứng
1x =−
. Tích
ab
nhận giá trị
bằng
A.
. B.
4
. C.
18−
. D.
2
.
Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 8
Chọn D
Đồ thị hàm số
2
y ax bx c= + +
là parabol nên
0a
.
Parabol đi qua điểm
( )
1;7A
nên ta có
2
7 .1 .1 4 3a b a b= + + + =
.
Trục đối xứng của parabol là đường thẳng
1x =−
nên
12
2
b
ba
a
−
= − =
.
Vậy ta có hệ:
3
20
ab
ab
+=
−=
1
1.2 2
2
a
ab
b
=
= =
=
.
Câu 3. Nghiệm của hệ phương trình
22
2 3 10
xy
xy
− = −
+=
là
A.
( ) ( )
; 2;2xy=
. B.
( ) ( )
; 3;6xy=
. C.
( ) ( )
; 2; 2xy= − −
. D.
( ) ( )
; 1; 2xy=−
.
Lời giải.
Tác giả: Trần Thanh Hà ; Fb: Hà Trần
Phản biện: Đồng Anh Tú; FB: Anh Tú
Chọn A
Ta có:
( )
22
2 2 2 2 2
2 2 2 3 10
2 3 10 7 14 2
xy
x y x y x
yy
x y y y
=−
− = − = − =
− + =
+ = = =
.
Vậy hệ phương trình đã cho có nghiệm là:
( ) ( )
; 2;2xy=
.
Câu 4. Cho đoạn thẳng
6AB =
. Tập hợp các điểm
M
thỏa mãn
22
18MA MB+=
là
A. một đoạn thẳng. B. một điểm. C. một đường tròn. D. một đường thẳng.
Lời giải
Tác giả: Trần kim Nhung ; Fb:Nhung trần thị Kim
Chọn B
Gọi
I
là trung điểm của
AB
0IA IB + =
và
3IA IB==
.
Giả sử
M
là điểm thỏa mãn bài toán.
Ta có:
22
22
18 18MA MB MA MB+ = + =
( ) ( )
22
18MI IA MI IB + + + =
( )
2 2 2
2 2 . 18MI MI IA IB IA IB + + + + =
2 2 2 2
2 18 0MI IA IB MI + + = =
.
Do đó:
M
trùng
I
.
Vậy tập hợp các điểm
M
thỏa mãn bài toán là một điểm.
Câu 5. Trong mặt phẳng tọa độ
Oxy
,
cho tam giác
ABC
vuông tại
( )
2;2A
. Biết
( )
4; 2C −
và
B Oy
. Tìm tọa
độ điểm
B
.
A.
( )
0;3B
. B.
( )
0; 3B −
. C.
( )
0;1B
. D.
( )
0; 1 .B −
Lời giải
Tác giả: Trần Quang Đạt; Fb: Quang Đạt
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 9
Chọn C
Do
B Oy
nên
B
có tọa độ
( )
0;y
,
y
.
Khi đó
( )
2; 2AB y= − −
;
( )
2; 4AC =−
.
Tam giác
ABC
vuông tại
A
nên
.0AB AC =
( ) ( ) ( )
2 .2 2 . 4 0y − + − − =
1y=
.
Vậy
( )
0;1B
.
Câu 6. Lớp
10D
có
37
học sinh, trong đó có
17
học sinh thích môn Văn,
19
học sinh thích môn Toán,
9
em
không thích môn nào. Số học sinh thích cả hai môn là
A.
2
học sinh. B.
6
học sinh. C.
13
học sinh. D.
8
học sinh.
Lời giải
Tác giả: Trịnh Duy Thanh; FB: Trịnh Duy Thanh
Chọn D
Gọi số học sinh thích cả hai môn là
x
(
0 17x
). Khi đó số học sinh chỉ thích môn Văn là
17 x−
,
số học sinh chỉ thích môn Toán là
19 x−
.
Ta có:
( ) ( )
9 17 19 37 8x x x x+ − + − + = =
.
Câu 7. Phương trình
4
4
22
x
x
xx
−
−
=
−−
có tất cả bao nhiêu nghiệm nguyên?
A.
1
. B. Vô số. C.
2
. D.
0
.
Lời giải
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen
Chọn C
Điều kiện xác định:
2x
.
Khi đó phương trình đã cho tương đương với
4 4 4 0 4x x x x− = − −
.
Kết hợp với điều kiện xác định ta có nghiệm của phương trình là
24x
.
Do
x
nên
3;4x
. Vậy phương trình có 2 nghiệm nguyên.
Câu 8. Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
2yx=−
cắt parabol
( )
2
:2P y x mx= − +
tại
đúng một điểm.
A.
3
5
m
m
=
=−
. B.
3m =
. C.
5m =−
. D.
m
.
Lời giải
Tác giả: Nguyễn Thị Hồng Hợp ; Fb: Nguyễn Thị Hồng Hợp
Chọn A
Phương trình hoành độ giao điểm của đường thẳng
d
:
2yx=−
và pararabol
( )
P
là:
( )
22
2 2 1 4 0x x mx x m x− = − + − + + =
(1)
Đường thẳng
d
cắt parabol
( )
P
tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép. Điều này
tương đương với
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 10
( )
2
2
3
1 4.4 2 15 0
5
m
m m m
m
=
= + − = + − =
=−
.
Câu 9. Cho các vectơ
a
,
b
có độ dài bằng
1
và
3 4 13ab−=
. Tính
( )
cos ,ab
.
A.
1
2
. B.
1
. C.
1
4
. D.
3
2
.
Lời giải
Tác giả: Nguyễn Thị Tnh ; Fb: Ngọc Tnh
Chọn A
Ta có:
3 4 13ab−=
2
3 4 13ab − =
( )
2
3 4 13ab − =
22
9 24 . 16 13a ab b − + =
.
( )
22
9 24 os , 16 13a a b c a b b − + =
( )
9.1 24.1.1. os , 16.1 13c a b − + =
.
( )
1
os ,
2
c a b=
.
Câu 10. Cho tam giác
ABC
nhọn có
3BC a=
và bán kính đường tròn ngoại tiếp tam giác
ABC
là
3Ra=
. Tính
số đo góc
A
.
A.
120=A
. B.
45=A
. C.
30=A
. D.
60=A
.
Lời giải
Tác giả: Thân Thế Luân ; Fb: Luan Vu
Chọn D
Áp dụng định lý sin trong tam giác
ABC
, ta có
33
2 sin
sin 2 2
23
= = = =
BC BC a
RA
AR
a
.
Suy ra
60=A
(do tam giác
ABC
nhọn).
Câu 11: Số nghiệm của hệ phương trình
22
5
5
xy x y
xy
+ + =
+=
là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Tác giả: Đồng Anh Tú; Fb: Anh tu
Chọn A
Đặt
=+
=
S x y
P xy
( Điều kiện:
2
4SP
)
Ta được hệ phương trình
2
5
25
+=
−=
SP
SP
( )
2
2
5
5
2 5 5
2 15 0
=−
=−


− − =
+ − =
PS
PS
SS
SS
5
5 10
=−
= − =
S
PS
hoặc
3
52
=
= − =
S
PS
.
Với
5; 10= − =SP
thì
2
4 25 40 15 0− = − = − SP
nên ta loại trường hợp này.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 11
Với
5; 10= − =SP
thì
2
4 9 8 1 0− = − = SP
nên khi đó
,xy
là nghiệm của phương trình
2
1
3 2 0
2
X
XX
X
=
− + =
=
Ta có nghiệm hệ phương trình là
( ; ) (1;2)xy=
hoặc
( ; ) (2;1)xy=
.
Câu 12. Cho tam giác
ABC
là tam giác đều,
O
là tâm đường tròn ngoại tiếp tam giác
ABC
. Tìm mệnh đề đúng
trong các mệnh đề sau.
A.
OA OB OC+=
. B.
2OA OB OC+=
. C.
OA OB CO+=
. D.
2OA OB CO+=
.
Lời giải
Tác giả: Thân Thế Luân; Fb: Luan Vu
Chọn C
Do
ABC
đều nên
O
cũng là trọng tâm của
ABC
.
Khi đó
0OA OB OC OA OB CO+ + = + =
.
Câu 13. Cho Parabol
( )
2
:2P y x bx c= − + +
có điểm
( )
2;10M
là điểm có tung độ lớn nhất. Tính giá trị của
c
.
A.
22
. B.
6.
C.
12.
D.
10.
Lời giải
Tác giả: Lê Văn Kỳ ; Fb: Lê Văn Kỳ
Chọn B
Từ đề bài suy ra
1.a =−
Ta có: điểm
( )
2;10M
là điểm có tung độ lớn nhất
( )
2;10M
là tọa độ đỉnh của
( )
P
.
( ) ( )
2
2
2
2
2
2
6
10 2 4
2;10
b
b
b
c
bc
MP
−
=
=
=
−
=
= − + +
.
Câu 14. Trong các hàm số sau đâu là hàm số bậc nhất?
A.
( )( )
2
1 1 2 .y x x x x= − + + +
B.
( )
2
1
2 1 .yx
x
= − −
C.
2
1.yx=−
D.
62
.
x
y
x
+
=
Lời giải
Tác giả: Lê Văn Kỳ ; Fb: Lê Văn Kỳ
Chọn A
Ta có
( )( )
2 2 2
1 1 2 1 2 2 1y x x x x x x x x= − + + + = − + + = +
là hàm số bậc nhất.
Câu 15. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.
:3 3
n
nn +
. B.
1 2 6 7
.
C.
6 4 10 7
. D.
( )
2
2
:2x x x −
.
Lời giải
Tác giả: Lê Thị Phương; Fb: Plus kính gửi
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 12
Chọn D
• Với
1n =
thì
3 3; 3 4
n
n= + =
nên đáp án A là đúng.
• Ta có mệnh đề
:"1 2"P
và mệnh đề
:"6 7"Q
là mệnh đề sai nên mệnh đề
PQ
hay mệnh
đề
1 2 6 7
là mệnh đề đúng. Đáp án B đúng.
• Ta có mệnh đề
:"6 4"P
là mệnh đề sai và mệnh đề
:"10 7"Q
là mệnh đề đúng nên mệnh đề
PQ
hay mệnh đề
6 4 10 7
là mệnh đề đúng. Đáp án C đúng.
• Với
1x = −
thì
( )
2
29x −=
;
2
1x =
nên mệnh đề
( )
2
2
:2x x x −
là mệnh đề sai.
Câu 16. Số nghiệm của phương trình
( )
2
3 9 20 0x x x− − + =
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Tác giả: Trần Văn Trưởng; FB: Trần Văn Trưởng
Chọn B
Điều kiện xác định:
3.x
Khi đó phương trình
=
− =
=
− + =
=
2
3
30
4 (loại) .
9 20 0
5 (loại)
x
x
x
xx
x
Vậy phương trình đã cho có 1 nghiệm.
Câu 17. Cho ba điểm bất kỳ
,,M N P
. Đẳng thức nào sau đây sai?
A.
PM NM NP=−
. B.
MN NP PM+ = −
. C.
MN MP PN=−
. D.
NP MP NM=+
.
Lời giải
Tác giả: Lê Xuân Sơn; Fb: Lê Xuân Sơn
Chọn C
Đẳng thức
MN MP PN=−
sai. (Đẳng thức
MN MP PN=−
chỉ đúng trong trường hợp đặc biệt
PN
).
Câu 18. Trong mặt phẳng tọa độ
Oxy
, cho
( ) ( )
1;3 ; 1; 8AB−−
. Tìm điều kiện của
a
để điểm
( )
;0Ma
thỏa mãn góc
AMB
là một góc tù.
A.
5;5a−
. B.
( )
5;a +
. C.
( )
;5a − −
. D.
( )
5
5;5 \ .
11
a

−


Lời giải
Tác giả và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình
Chọn D
Ta có:
( ) ( )
1 ;3 ; 1 ; 8 ;MA a MB a− − − −
( )
( )( )
( )
( )
22
1 1 24
cos ;
1 9 1 64
aa
MA MB
aa
− − − −
=
− + − − +
.
Góc
AMB
là một góc tù
( )
;MA MB
là một góc tù
( )
cos ; 0MA MB
và
;MA MB
không ngược
hướng.
+)
;MA MB
cùng phương
( )
85
1 1 8 8 3 3
3 11
a a a a a − − = − − − + = − − =
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 13
Khi đó
6 16
;3 ; ; 8
11 11
MA MB
−
−
nên
;MA MB
ngược hướng. Do đó
5
11
a
(1)
+)
( )
cos ; 0MA MB
( )( )
( )
( )
2
22
1 1 24
0 25 0 5 5 (2)
1 9. 1 64
aa
aa
aa
− − − −
− −
− + − − +
Từ (1) và (2),
( )
5
5;5 \
11
a

−


.
Câu này ở đáp D nguyên văn trong đề gốc là: D.
( )
5;5a−
.
Chúng tôi nghĩ đề ra sai và đã sửa lại thành D.
( )
5
5;5 \ .
11
a

−


Câu 19: Một học sinh giải phương trình
( )
2
2 4 2x x *+=
như sau:
Bước 1: Điều kiện xác định là
¡
.
Bước 2:
( )
22
2 4 4* x xÛ + =
Bước 3:
2
2xÛ=
. Vậy phương trình có nghiệm
2x =
và
2x =-
Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào?
A. Lời giải đúng. B. Lời giải sai từ bước 1.
C. Lời giải sai từ bước 2. D. Lời giải sai từ bước 3.
Lời giải
Tác giả: Trần Thị Thủy; Fb: Thủy Trần
Chọn C
2
2 2 2
0
2 0 0
2 4 2 2
2 4 4 2
2
x
xx
x x x
x x x
x
ì
ìì
³
³³
ï
ïï
ï ï ï
+ = Û Û Û Û =
í í í
ï ï ï
+ = =
=±
ï ï ï
îî
î
.
Chọn C.
Câu 20. Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng?
A.
3
3y x x=+
. B.
33y x x= + + −
. C.
( )
2
1yx=+
. D.
1x
y
x
−
=
.
Lời giải
Tác giả :Trần Thị Phượng Uyên, FB: UyenTran
Chọn B
Đồ thị hàm số nhận trục tung làm trục đối xứng khi hàm số là hàm chẵn
Xét hàm số
33y x x= + + −
, ta có:
( ) ( )
3 3 3 3f x x x x x f x− = − + + − − = − + + =
Suy ra hàm số trên là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
Câu 21. Phương trình
22
7 6 2 4x x x x− + = − +
có bao nhiêu nghiệm nguyên âm?
A. 2. B. 0. C. 1. D. 3.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 14
Tác giả : Chu Quốc Hùng, FB: Chu Quốc Hùng Edu
Chọn B
Ta có:
22
22
22
2
2
2
5
7 6 2 4
7 6 2 4 2
5
7 6 2 4
2 9 10 0
5
2
x
x
x x x x
x x x x x
x x x x
xx
x
=
=
− + = − +
− + = − + =
− + = − + −
− + =
=
.
Vậy phương trình không có nghiệm nguyên âm.
Câu 22. Có bao nhiêu giá trị của tham số
m
để hai đường thẳng
( )
1
: 1 3 2d y m x m= − + −
và
( )
2
2
: 1 2 1d y m x m= − + −
song song với nhau ?
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải:
Chọn C.
( )
1
: 1 3 2d y m x m= − + −
có hệ số
1
1am=−
,
1
32bm=−
( )
2
2
: 1 2 1d y m x m= − + −
có hệ số
2
2
1am=−
,
1
21bm=−
1
d
và
2
d
song song
12
12
aa
bb
=
2
11
3 2 2 1
mm
mm
− = −
− −
0
1
1
m
m
m
=
=
0m =
.
Câu 23. Cho tam giác
ABC
có
4cmAB =
;
12cmAC =
và góc
120BAC =
. Tính diện tích tam giác
ABC
.
A.
12 3
(
2
cm
). B.
24 3
(
2
cm
). C.
12
(
2
cm
). D.
24
(
2
cm
).
Lời giải
Chọn A
Diện tích tam giác
ABC
là
1
. .sin
2
S AB AC BAC=
1
.4.12.sin120
2
=
12 3=
(
2
cm
)
Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của a?
A.
3aa
. B.
22
2aa−
. C.
23aa− −
. D.
1
3
aa−
.
Lời giải
Chọn C
A.
3 2 0 0a a a a
B.
2 2 2
2 3 0 0a a a a −
C.
2 3 2 3aa− −
(luôn đúng với mọi a).
D.
14
00
33
a a a a −
Câu 25. Cho tam giác
ABC
thỏa mãn
2 2 2
2 . 0BC AC AB BC AC+ − − =
. Khi đó, góc
C
có số đo là
A.
150C =
. B.
60C =
. C.
45C =
. D.
30C =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 15
Lời giải
Tác giả:ThanhLoan ; Fb: ThanhLoan
Chọn C
Theo đề ra ta có:
2 2 2
2 . 0BC AC AB BC AC+ − − =
2 2 2
2.BC AC AB BC AC + − =
2 2 2
2
.
BC AC AB
BC AC
+−
=
2cos 2 0C − =
2
cos
2
C=
45C =
.
Câu 26. Cho hình bình hành
ABCD
có
1, 2, 60AB AD DAB= = =
. Tính độ dài cạnh
AC
.
A.
3
. B.
7
3
. C.
7
. D.
5
.
Lời giải
Tác giả: Nguyễn Thị Huệ ; Fb: Nguyễn Thị Huệ
Chọn C
Gọi
O
là tâm của hình bình hành
ABCD
. Xét tam giác
ABD
, áp dụng định lý cosin ta có,
222
1
2. . .cos60 1 4 2.1.2. 3
2
BD AB AD AB AD= + − = + − =
.
Mặt khác , áp dụng công thức tính độ dài đường trung tuyến
AO
trong tam giác
ABD
, ta có,
2 2 2
2
1 4 3 7
2 4 2 4 4
AB AD BD
AO
++
= − = − =
. Suy ra
7
2
AO =
27AC AO = =
.
Vậy
7AC =
.
Câu 27. Cho hàm số
2
( 0)y ax bx c a= + +
có bảng biến thiên như hình vẽ dưới đây
Xác định dấu của
,,abc
A.
0, 0, 0abc
. B.
0, 0, 0a b c
. C.
0, 0, 0abc
D.
0, 0, 0a b c
.
Lời giải
Tác giả:Huỳnh Hữu Hùng ; Fb:Huuhung Huynh
Chọn B
Từ bảng biến thiên ta thấy đồ thị hàm số có bề lõm quay xuống nên
0a
.
Vì
0
2
b
a
−
nên
0b
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 16
Giao điểm của đồ thị hàm số với trục
Oy
là điểm
(0; 1)−
nên
10c = −
.
Câu 28. Cho hàm số
2
( ) 4 2y f x x x= = − +
trong các mệnh đề dưới đây mệnh đề nào đúng ?
A.
( ) ( )
2019 2019
23ff− −
.
B.
( ) ( )
2019 2019
23ff
.
C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
D. Đồ thị hàm số nhận đường thẳng
2x =−
làm trục đối xứng.
Lời giải
Tác giả:Huỳnh Hữu Hùng ; Fb:Huuhung Huynh
Chọn B
+) Hàm số đã cho là hàm số bậc
2
chỉ có đúng một trục đối xứng là đường thẳng
2
2
b
x
a
= − =
làm trục đối xứng
D sai.
+)
( )
2 2 0f = −
C sai.
+) Hệ số
10a =
và
2
2
b
a
−=
nên hàm số đồng biến trên khoảng
( )
2;+
, nghịch biến trên khoảng
( )
;2−
. Từ
đó, vì
2019 2019
2 2 3 − −
nên
( ) ( )
2019 2019
23ff− −
A sai.
Ta cũng có
2019 2019
322
nên
2019 2019
(2 ) (3 )ff
B đúng.
Câu 29. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
5;3 , 2; 1 , 1;5A B C−−
. Tìm tọa độ điểm
H
là
trực tâm tam giác
ABC
.
A.
( )
3;2H
. B.
( )
3; 2H −
. C.
7
2;
3
H



. D.
7
2;
3
H

−−


.
Lời giải
Tác giả: Hà Minh Yên ; Fb:Hà Minh Yên
Chọn A
H
C
B
A
Gọi
( )
;H x y
là trực tâm của tam giác
ABC
. Khi đó
.0
.0
AH BC
BH AC
=
=
(*).
( ) ( )
5; 3 ; 3;6AH x y BC= − − = −
;
( ) ( )
2; 1 ; 6;2BH x y AC= − + = −
.
(*)
( ) ( )
( ) ( )
3 5 6 3 0
6 2 2 1 0
xy
xy
− − + − =
− − + + =
2 1 3
3 7 2
x y x
x y y
− = − =



− = =

.
Vậy :
( )
3;2H
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 17
Câu 30. Tổng các nghiệm của phương trình
( ) ( )
42
3 2 4 3 2 0xx− − − − =
là
A.
1−
. B.
4
32−
. C.
0
. D.
2
32−
.
Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp
Chọn C
Đặt
2
tx=
, điều kiện:
0t
.
Khi đó phương trình
( ) ( )
42
3 2 4 3 2 0xx− − − − =
( )
1
trở thành:
( ) ( )
( )
2
3 2 4 3 2 0 *tt− − − − =
.
Nhận thấy phương trình
( )
*
có
( )
2
. 3 2 0ac= − −
nên phương trình
( )
*
có hai nghiệm phân biệt:
1
0t
(loại)
2
,0t
(nhận).
Suy ra phương trình
( )
1
có 2 nghiệm là:
1 2 2 2
,x t x t= − =
.
Vậy
1 2 2 2
0x x t t+ = − + =
.
Câu 31. Cho
,ab
là hai số thực tùy ý. Mệnh đề nào sau đây đúng?
A. Nếu
22
ab
thì
ab
. B. Nếu
ab
thì
22
ab
.
C. Nếu
ab
và
0a
thì
22
ab
. D. Nếu
ab
và
0b
thì
22
ab
.
Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp
Chọn C
Đáp án A sai với
2, 1ab= − = −
.
Đáp án B sai với
1, 0ab= − =
.
Đáp án C đúng vì
22
0
0
ab
a b a b
a
.
Đáp án D sai với
1, 1ab= − =
.
Câu 32. Trong mặt phẳng tọa độ
Oxy
, cho hình bình hành
ABCD
có
( )
1;2A
,
( )
2;4B −
,
( )
0;3C
. Tìm tọa độ
điểm
D
.
A.
( )
3;1−
. B.
( )
3;1
. C.
( )
3; 1−
. D.
( )
3; 1−−
.
Lời giải
Tác giả: Phạm Văn Tuân; Fb: mr.vtuan.
Chọn B
Vì
ABCD
là hình bình hành nên
AB DC=
.
Ta có:
( )
3;2AB =−
;
( )
;3
DD
DC x y= − −
.
Do
AB DC=
, suy ra
33
3 2 1
DD
DD
xx
yy
− = − =


− = =

.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 18
Vậy tọa độ điểm
D
là
( )
3;1
.
Câu 33. Giá trị lớn nhất của hàm số
2
3 2 5y x x= − + +
trên
2
;1
3

−


là
A.
16
3
. B.
5
. C.
1
. D.
7
3
.
Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh
Chọn A
Cách 1: Hàm số
2
3 2 5y x x= − + +
là hàm số bậc hai có hệ số
30a = −
và hoành độ đỉnh là
12
;1
33
I
x

= −


.
Bảng biến thiên của hàm số trên đoạn
2
;1
3

−


là:
Vậy giá trị lớn nhất của hàm số trên
2
;1
3

−


là
16
3
.
Cách 2: Ta có:
62yx
= − +
;
1
0
3
yx
= =
.
Vì
27
33
y

−=


;
( )
14y =
;
1 16
33
y

=


nên
2
;1
3
16
max
3
y

−


=
.
Cách 3: Sử dụng chức năng MODE 7:
Câu 34. Cho tam giác
ABC
có
..AB BC BC AC=−
. Tam giác
ABC
có tính chất gì?
A.
ABC
vuông tại
A
. B.
ABC
cân tại
B
.
C.
ABC
vuông tại
B
. D.
ABC
cân tại
A
.
Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh
Chọn D
Cách 1:
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 19
Gọi
M
là trung điểm của
BC
2AB AC AM + =
.
Ta có:
( )
. . . 0AB BC BC AC BC AB AC= − + =
.2 0BC AM BC AM = ⊥
.
Vậy
ABC
cân tại
A
.
Cách 2:
Ta có:
. . . .AB BC BC AC BABC CBCA= − − = −
. .cos . .cosBABC B CBCA C=
.cos .cosAB B AC C=
2 2 2 2 2 2
..
2. . 2. .
BC BA AC CA CB AB
AB AC
BC BA CACB
+ − + −
=
2 2 2 2 2 2
BC BA AC CA CB AB + − = + −
22
2A 2.B AC=
AB AC=
Vậy
ABC
cân tại
A
.
Câu 35. Cho tam giác
ABC
có
10AB =
,
17AC =
,
15BC =
. Tính
.AB AC
uuur uuur
.
A.
164
. B.
164−
. C.
82−
. D.
82
.
Lời giải
Tác giả:Trần Minh; Fb: Tran Minh
Chọn D
Ta có:
( )
2
2
2
BC BC AC AB= = −
22
2.AB AB AC AC= − +
22
2.AB AB AC AC= − +
Vậy
2 2 2
.
2
AB AC BC
AB AC
+−
=
uuur uuur
2 2 2
10 17 15
. 82
2
AB AC
+−
= =
uuur uuur
.
Câu 36. Tập xác định của hàm số
2
42
12
xx
y
xx
− + +
=
−−
là
A.
2;4−
. B.
( ) ( )
3; 2 2;4− − −
. C.
( )
2;4−
. D.
)
2;4−
.
Lời giải
Tác giả: Bùi Văn Khánh; Fb:Khánh Bùi Văn
Chọn D
ĐKXĐ:
2
4
40
2
2 0 2 4
3
12 0
4
x
x
x
xx
x
xx
x
−
−

+ −

−

− −
.
Vậy, tập xác định của hàm số là
)
2;4D =−
.
Câu 37. Tìm giá trị của tham số
m
để đỉnh
I
của đồ thị hàm số
2
6y x x m= − + +
thuộc đường thẳng
2019yx=+
.
A.
2020m =
. B.
2000m =
. C.
2036m =
. D.
2013m =
.
Lời giải
Tác giả: Bùi Văn Khánh ; Fb:Khánh Bùi Văn
Chọn D
Đồ thị hàm số
2
6y x x m= − + +
là parabol có đỉnh
( )
3;9Im+
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 20
Đỉnh
( )
3;9Im+
thuộc đường thẳng
2019 9 3 2019 2013y x m m= + + = + =
.
Câu 38. Cho tam giác
ABC
vuông cân tại
A
có
2BC a=
. Tính độ dài
BA BC+
.
A.
25a
. B.
5a
. C.
3a
. D.
23a
.
Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ
Chọn B
ABC
vuông cân tại
A
có
2BC a=
nên
AB AC a==
Gọi
M
là trung điểm
AC
Ta có
2BA BC BM+=
2BM=
22
2 AB AM=+
2
2
25
2
a
aa

= + =


Câu 39. Biết đường thẳng
:4d y x= − +
cắt parabol
( )
2
:2P y x x=−
tại hai điểm phân biệt
A
và
B
. Tìm tọa độ
trọng tâm
G
của tam giác
OAB
.
A.
17
;
33
G



. B.
( )
1; 2G −
.
C.
1 17 9 17
;
33
G

−−



. D.
17
;
22
G



.
Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ
Chọn A
Xét phương trình hoành độ giao điểm của
d
và
( )
P
:
2
24x x x− = − +
( )
2
4 0 *xx − − =
( )
*
có hai nghiệm phân biệt
12
;xx
thỏa mãn:
12
1xx+=
. Khi đó giao điểm của
d
và
( )
P
lần lượt là
( ) ( )
1 1 2 2
; 4 , ; 4A x x B x x− + − +
Tọa độ trọng tâm
G
của tam giác
OAB
là
1 2 1 2
8
;
33
x x x x
G
+ − − +



hay
17
;
33
G



Câu 40. Cho hệ phương trình
21
2 2 1
mx y m
x my m
+ = +
+ = −
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hệ phương
trình đã cho vô nghiệm.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 21
A.
2.m =−
B.
2.m −
C.
2.m
D.
2.m =
Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta
Chọn A
Ta có các định thức
2 2 2
4; 3 2; 2 3 2
xy
D m D m m D m m= − = − + = − −
.
Hệ vô nghiệm thì
2
0
2
m
D
m
=
=
=−
+ Khi
2: 0; 0.
xy
m D D= = =
( Hệ vô số nghiệm).
+ Khi
2: 12; 12.
xy
m D D= − = =
( Hệ vô nghiệm).
Câu 41. Giá trị nhỏ nhất của hàm số
6
()
22
x
fx
x
=+
−
với
2x
là số có dạng
3ab+
(
,ab
là các số nguyên).
Tính
22
.ab+
A.
5.
B.
6.
C.
3.
D.
4.
Lời giải
Tác giả: Tạ Tiên Thanh ; Fb: Thanh Ta
Chọn A
Với
2x
thì
20x−
nên
6 2 6 2 6
( ) 1 2 . 1 2 3 1
2 2 2 2 2 2
x x x
fx
x x x
−−
= + = + + + = +
− − −
.
Dấu bằng xảy ra khi và chỉ khi
( )
26
2 2 3 vì 2
22
x
xx
x
−
= = +
−
Vậy giá trị nhỏ nhất của hàm số
()fx
là
22
2 3 1 2; 1 5.a b a b+ = = + =
Chú ý: Trong đề gốc thiếu giả thiết
,ab
là các số nguyên, chúng tôi đã phải thêm điều kiện này vào trong đề ra để
bài toán có thể giải được.
Câu 42. Số các giá trị thực của tham số
m
để phương trình
( )( )
21
0
1
x mx
x
−+
=
+
có nghiệm duy nhất là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang
Chọn A
( )( )
( )
21
01
1
x mx
x
−+
=
+
Điều kiện xác định :
1x −
.
Với điều kiện trên, phương trình
( )
1
( )( )
20
2 1 0
10
x
x mx
mx
−=
− + =
+=
( )
2
12
x
mx
=
=−
Phương trình
( )
1
có nghiệm duy nhất
( )
2
vô nghiệm hoặc
( )
2
có nghiệm
2x =
hoặc
( )
2
có nghiệm
1x =−
.
(2) vô nghiệm khi
0m =
; (2) có nghiệm
2x =
khi
1
2
m =−
; (2) có nghiệm
1x =−
khi
1m =
.
Vậy có 3 giá trị của
m
thỏa mãn yêu cầu bài toán.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 22
Câu 43. Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
21x x m− + =
có hai nghiệm phân biệt.
A.
0m
. B.
0m
. C.
1m
hoặc
0m =
. D.
01m
.
Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang
Chọn C
42
21x x m− + =
(1)
Đặt
2
tx=
(
0t
).
Khi đó phương trình (1) trở thành:
2
21t t m− + =
2
2 1 0t t m − + − =
. (2)
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt trái dấu hoặc có
nghiệm kép dương
0
'0
0
ac
S
=
10
0
20
m
m
−
=
1
0
m
m
=
.
Câu 44. Tìm tất cả các giá trị thực của tham số
m
để phương trình
32
0x mx x m− − + =
có ba nghiệm thực phân
biệt.
A.
1m −
. B.
1m 
. C.
1m
hoặc
0m =
. D.
01m
.
Lời giải
Tác giả: ; Fb:
Chọn B
( ) ( )
( )
3 2 2 2 2
1
0 ( 1) 1 0 1 0
x
x mx x m x x m x x x m
xm
=
− − + = − − − = − − =
=
.
ycbt
1m
.
Câu 45. Cho phương trình
2
10x mx m− + + + =
với
m
là tham số thực. Tính tổng
S
tất cả các giá trị thực của tham
số
m
để phương trình có hai nghiệm phân biệt
12
,xx
thỏa mãn
12
4xx+=
.
A.
2S =
B.
2S =−
. C.
4S =−
D.
5S =
.
Lời giải
Tác giả: ; Fb:
Chọn B
Phương trình có hai nghiệm phân biệt
12
;0xxÛ D >
( ) ( )
2
2
4 1 0 2 0 2m m m mÛ + + > Û + > Û ¹ -
.
Khi đó phương trình có hai nghiệm phân biệt:
( ) ( )
12
22
1, 1
22
m m m m
x x m
− + + − − +
= = − = = +
−−
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 23
Ta có
12
1 3 2
4 1 1 4 1 3 ( )
1 3 4
mm
x x m m tm
mm
+ = =
+ = + + = + =
+ = − = −
.
Suy ra
2S =−
.
Câu 46: Cho phương trình
2
10 2x x m x− + = −
. Tìm tất cả các giá trị thực của tham số
m
để phương trình đã cho
vô nghiệm .
A.
16 20m
. B.
3 16m−
C.
m
. D.
16m
.
Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh
Chọn D.
2
10 2x x m x− + = −
( )
2
2
20
10 2
x
x x m x
−
− + = −
22
2
10 4 4
x
x x m x x
− + = − +
2
64
x
xm
=−
2
4
6
x
m
x
−
=
Để phương trình vô nghiệm thì
4
2 4 12 16
6
m
mm
−
−
.
Câu 47: Tập tất cả các giá trị của tham số
m
để phương trình
22
1x x m+ − =
có tập nghiệm là
;ab
. Tính
S a b=+
?
A.
0.
B.
9
.
4
C.
1.
D.
1
.
4
Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh.
Chọn B
22
1x x m+ − =
2
22
10
(1 ) 1 1 0
x
x x m
−
− − + − + − =
22
11
(1 ) 1 1 0
x
x x m
−
− − + − + − =
Đặt
2
1 xt−=
. Điều kiện
0;1t
. Phương trình
(*)
trở thành :
2
1t t m− + + =
(**)
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số
2
( ) 1f t t t= − + +
trên
0;1
và đường
thẳng
ym=
vuông góc với trục
Oy
.
Xét đồ thị hàm số
2
( ) 1f t t t= − + +
là đường parabol có đỉnh là điểm
15
;
24
I



, vì
10a = −
nên bề
lõm quay xuống dưới. Ta có bảng biến thiên sau :
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 24
Dựa vào bảng biến thiên, ta có: Phương trình (**) có nghiệm
5
1;
4
m



.
Vậy
5
1;
4
ab==
59
1
44
S a b = + = + =
.
Câu 48: Cho hàm số
2
2y x x=−
có đồ thị như hình vẽ. Gọi
S
là tập các giá trị nguyên của
m
đề phương trình
2
21x x m− + =
có hai nghiệm phân biệt. Tính tổng các phần tử của tập
S
.
A.
1−
. B.
2
. C.
4
. D.
0
.
Lời giải
Tác giả: Trần Thảo; Facebook: Trần Thảo
Chọn B
( )
( )
22
2
22
2 1 2 1 1
21
2 1 2 1 2
x x m x x m
x x m
x x m x x m

− + = − = −
− + =

− + = − − = − −


Xét phương trình
2
2x x k−=
(3). Số nghiệm của phương trình này là số giao điểm của đồ thị hàm số
2
2y x x=−
và đường thẳng
yk=
.
Từ đồ thị hàm số
2
2y x x=−
ta có kết luận sau:
k
Số giao điểm
Kết luận về số nghiệm của PT (3)
1k −
0
Phương trình vô nghiệm
1k =−
2
Phương trình có 2 nghiệm phân biệt
10k−
4
Phương trình có 4 nghiệm phân biệt
0k =
3
Phương trình có 3 nghiệm phân biệt
0k
2
Phương trình có 2 nghiệm phân biệt
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 25
Do
( )
11m m m− − −
nên để phương trình đã cho có hai nghiệm phân biệt thì phương trình
( )
1
có
hai nghiệm phân biệt và phương trình
( )
2
vô nghiệm.
Điều đó tương đương với :
1 1 0
2
1 1 2
01
1 0 1
mm
m
mm
m
mm
− − −

=


− = − =





−


.
Do
m
nên
2m =
. Vậy
2S =
. Tổng các phần tử của tập
S
là
2
.
Câu 49. Trong hệ tọa độ
Oxy
cho ba điểm
( )
1; 4A −
,
( )
4;5B
và
( )
0; 9C −
. Điểm
M
di chuyển trên trục
Ox
. Đặt
2 2 3Q MA MB MB MC= + + +
. Biết giá trị nhỏ nhất của
Q
có dạng
ab
trong đó
a
,
b
là các số nguyên
dương và
a
,
20b
. Tính
ab−
.
A.
15−
. B.
17−
. C.
14−
. D.
11−
.
Lời giải
Tác giả: Nguyễn Thị Thanh Mai; Fb: Thanh Mai Nguyen
Chọn D
Giả sử
( )
;0M x Ox
. Ta có:
( )
1 ; 4MA x= − −
,
( )
4 ;5MB x=−
,
( )
;9MC x= − −
.
( )
2 9 3 ;6MA MB x + = −
,
( )
4 2 ; 4MB MC x+ = − −
.
Do đó
( ) ( ) ( )
2 2 2
2
2 9 3 6 3 4 2 4Q x x= − + + − + −
( ) ( )
22
22
6 3 2 6 2 ( 2)xx= − + + − + −
( )
6 ME MF=+
.
Trong đó
( )
3;2E
,
( )
2; 2F −
.
Ta có
17ME MF EF+ =
6 17Q
Dấu “ = “ xảy ra
M
là giao điểm của đoạn
EF
và trục
Ox
5
( ;0)
2
M
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 26
Suy ra
Q
đạt giá trị nhỏ nhất là
6 17
. Do đó theo giả thiết ta có
6
17
a
b
=
=
.Vậy
11ab− = −
.
Câu 50. Cho
,xy
thoả mãn
22
x y a+=
. Xác định
a
, biết rằng giá trị lớn nhất của
23P x y=+
với
,0xy
là
117
.
A.
9a =
. B.
13a =
. C.
5a =
. D.
33a =
.
Lời giải
Tác giả: Vũ Thị Thu Huyền; Fb: HuyenVu
Chọn A.
Ta có :
22
0a x y= +
( )
( )( )
2
2 2 2 2 2 2
2 3 2 3 13P x y x y P a= + + +
.
22
2
13
13 ( 0, 0)
23
3
13
a
x
xy
P a do x y
a
x y a
y
=
=

=


+=
=
Vậy
13MaxP a=
. Theo giả thiết, ta có:
13 117 9aa= =
.
---------- HẾT ----------
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
TRƯỜNG LƯƠNG THẾ VINH - HÀ NỘI
ĐỀ THI HỌC KÌ I NĂM HỌC 2019 - 2020
--------------------------------------
Môn thi: TOÁN - Khối: 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
---------------------------- MÃ ĐỀ THI: 281 Câu 1:
Số các giá trị nguyên của m để phương trình 2
x − 3x − m = 0 có bốn nghiệm phân biệt là A. vô số. B. 0 . C. 2 . D. 4 . Câu 2: Cho parabol (P) 2
: y = ax + bx + 4 đi qua điểm A(1;7) và có trục đối xứng x = 1 − . Tích ab nhận giá trị bằng A. 6 − . B. 4 . C. 18 − . D. 2 . x − 2y = 2 − Câu 3:
Nghiệm của hệ phương trình  là 2x + 3y = 10
A. ( x; y) = (2;2) .
B. ( x; y) = (3;6).
C. ( x; y) = ( 2
− ;− 2) . D. (x; y) = (1;− 2) . Câu 4:
Cho đoạn thẳng AB = 6. Tập hợp các điểm M thỏa mãn 2 2
MA + MB = 18 là
A. một đoạn thẳng. B. một điểm.
C. một đường tròn.
D. một đường thẳng. Câu 5:
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC vuông tại A(2;2) . Biết C (4;− 2) và B Oy . Tìm
tọa độ điểm B . A. B (0;3) . B. B (0; 3 − ) . C. B (0; ) 1 . D. B (0; − ) 1 . Câu 6:
Lớp 10D có 37 học sinh, trong đó có 17 học sinh thích môn Văn, 19 học sinh thích môn Toán, 9
em không thích môn nào. Số học sinh thích cả hai môn là A. 2 học sinh. B. 6 học sinh. C. 13 học sinh. D. 8 học sinh. 4 − x 4 − x Câu 7: Phương trình =
có tất cả bao nhiêu nghiệm nguyên? x − 2 x − 2
A. 1. B. Vô số. C. 2 . D. 0 . Câu 8:
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = x − 2 cắt parabol (P) 2
: y = x − mx + 2
tại đúng một điểm. m = 3 A.  . B. m = 3 . C. m = 5 − . D. m . m = 5 − Câu 9:
Cho các vectơ a , b có độ dài bằng 1 và 3a − 4b = 13 . Tính cos(a,b) . 1 1 3 A. . B. 1. C. . D. . 2 4 2
Câu 10: Cho tam giác ABC nhọn có BC = 3a và bán kính đường tròn ngoại tiếp tam giác ABC là R = a 3 .
Tính số đo góc A .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 A. A =120 . B. A = 45 . C. A = 30 . D. A = 60 .
xy + x + y = 5
Câu 11: Số nghiệm của hệ phương trình  là 2 2 x + y = 5
A. 2 . B. 0 . C. 1. D. 3 .
Câu 12: Cho tam giác ABC là tam giác đều, O là tâm đường tròn ngoại tiếp tam giác ABC . Tìm mệnh đề
đúng trong các mệnh đề sau.
A. OA + OB = OC .
B. OA + OB = 2OC .
C. OA + OB = CO.
D. OA + OB = 2CO .
Câu 13: Cho Parabol (P) 2
: y = −x + 2bx + c có điểm M (2;10) là điểm có tung độ lớn nhất. Tính giá trị của c . A. 22 . B. 6. C. 12. D. 10.
Câu 14: Trong các hàm số sau đâu là hàm số bậc nhất?
A. y = ( − x)( + x) 2 1 1 + x + 2 . x B. y = ( − )2 1 2 1 x − . x 6 + 2x C. 2 y = 1− x . D. y = . x
Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A.   : 3n nn + 3 .
B. 1  2  6  7 .
C. 6  4 10  7 . D. x   (x − )2 2 : 2  x .
Câu 16: Số nghiệm của phương trình − x ( 2 3
x − 9x + 20) = 0 là: A. 0 . B. 1. C. 2 . D. 3 .
Câu 17: Cho ba điểm bất kỳ M , N , P . Đẳng thức nào sau đây sai?
A. PM = NM − NP .
B. MN + NP = −PM . C. MN = MP − PN . D. NP = MP + NM .
Câu 18: Trong mặt phẳng tọa độ Oxy , cho A(1; ) 3 ; B( 1 − ; 8
− ). Tìm điều kiện của a để điểm M ( ;0 a ) thỏa
mãn góc AMB là một góc tù.   A. a  5 − ;  5 .
B. a (5;+) . C. a (− ;  5 − ) . D. a  (− ) 5 5;5 \  . 11  
Câu 19: Một học sinh giải phương trình 2
2x + 4 = 2x (*) như sau:
Bước 1: Điều kiện xác định là ¡ . Bước 2: (*) 2 2 Û 2x + 4 = 4x Bước 3: 2
Û x = 2 . Vậy phương trình có nghiệm x = 2 và x = - 2
Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào? A. Lời giải đúng.
B. Lời giải sai từ bước 1.
C. Lời giải sai từ bước 2.
D. Lời giải sai từ bước 3.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 2
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Câu 20: Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng? x −1 A. 3
y = x + 3x .
B. y = x + 3 + x − 3 . C. y = ( x + )2 1 . D. y = . x
Câu 21: Phương trình 2 2
x − 7x + 6 = x − 2x + 4 có bao nhiêu nghiệm nguyên âm? A. 2. B. 0. C. 1. D. 3.
Câu 22: Có bao nhiêu giá trị của tham số m để hai đường thẳng d : y = m −1 x + 3m − 2 và 1 ( ) d : y = ( 2
m −1 x + 2m −1 song song với nhau? 2 ) A. 3 . B. 2 . C. 1. D. 0 .
Câu 23: Cho tam giác ABC có AB = 4cm; AC =12cm và góc BAC = 120 . Tính diện tích tam giác ABC . A. 12 3 ( 2 cm ). B. 24 3 ( 2 cm ). C. 12 ( 2 cm ). D. 24 ( 2 cm ).
Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của a? 1
A. a  3a . B. 2 2 a  −2a .
C. 2 − a  3− a .
D. a  −a . 3
Câu 25: Cho tam giác ABC thỏa mãn 2 2 2
BC + AC − AB − 2B .
C AC = 0 . Khi đó, góc C có số đo là A. C = 150 .
B. C = 60 . C. C = 45 . D. C = 30 .
Câu 26: Cho hình bình hành ABCD có AB =1, AD = 2, DAB = 60 . Tính độ dài cạnh AC . 7 A. 3 . B. . C. 7 . D. 5 . 3 Câu 27: Cho hàm số 2
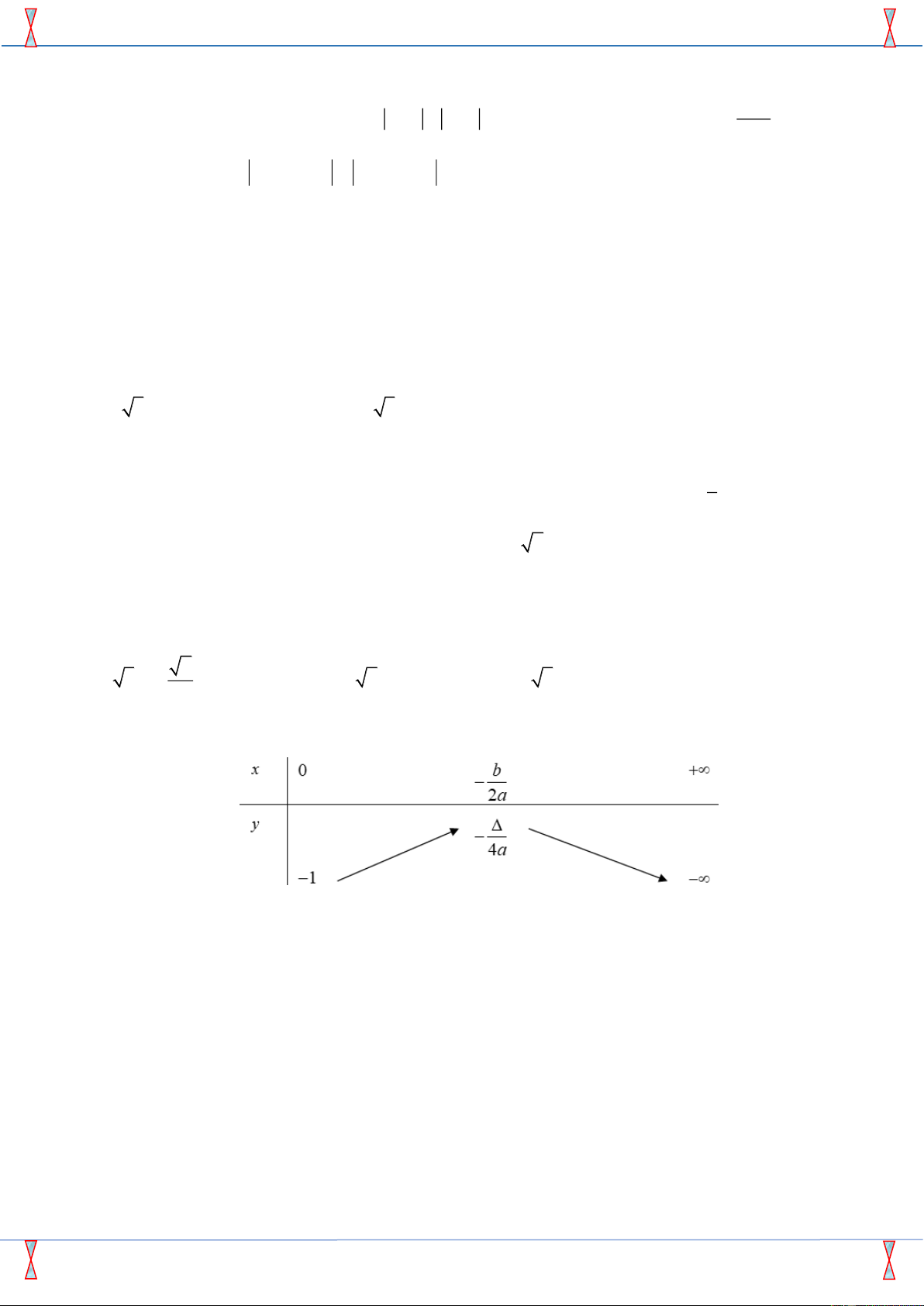
y = ax + bx + c (a  0) có bảng biến thiên như hình vẽ dưới đây
Xác định dấu của a,b, c
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 . C. a  0, b  0, c  0
D. a  0, b  0, c  0 . Câu 28: Cho hàm số 2
y = f (x) = x − 4x + 2 trong các mệnh đề dưới đây mệnh đề nào đúng? A. f ( 2019 − )  f ( 2019 2 −3 ).
B. f ( 2019 )  f ( 2019 2 3 ).
C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
D. Đồ thị hàm số nhận đường thẳng x = 2 − làm trục đối xứng.
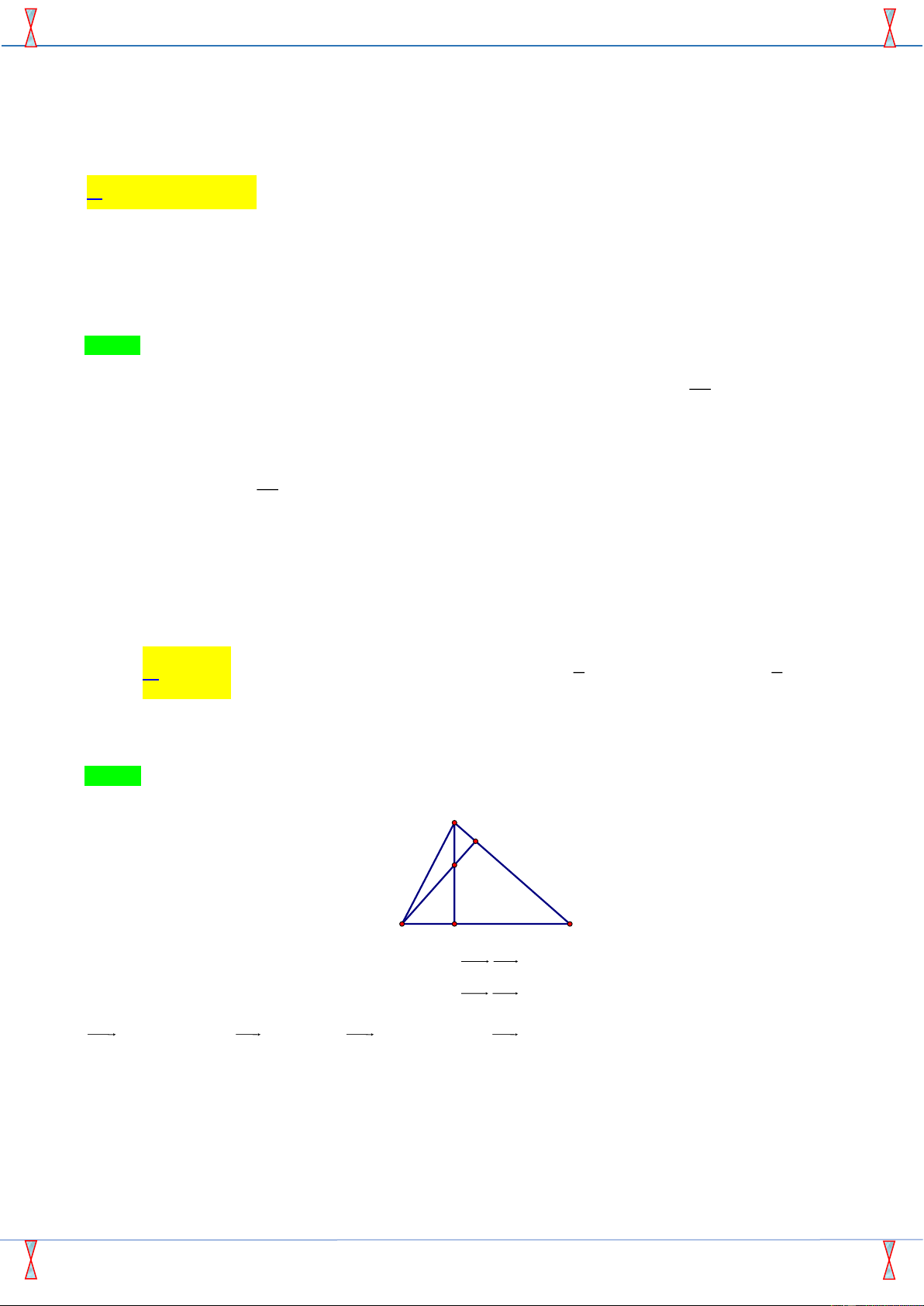
Câu 29: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(5; ) 3 , B(2;− ) 1 , C ( 1
− ;5). Tìm tọa độ điểm
H là trực tâm tam giác ABC .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 3
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020  7   7  A. H (3;2) . B. H (3; 2 − ). C. H 2;   . D. H 2; − −   .  3   3 
Câu 30: Cho a, b là hai số thực tùy ý. Mệnh đề nào sau đây đúng? A. Nếu 2 2
a b thì a b .
B. Nếu a b thì 2 2 a b .
C. Nếu a b và a  0 thì 2 2 a b .
D. Nếu a b và b  0 thì 2 2 a b .
Câu 31: Tổng các nghiệm của phương trình ( − ) 4 2 3
2 x − 4x − ( 3 − 2) = 0 là 4 2 A. −1. B. . C. 0 . D. . 3 − 2 3 − 2
Câu 32: Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có A(1;2) , B( 2 − ;4) , C(0; ) 3 . Tìm tọa độ điểm D . A. ( 3 − ; ) 1 . B. (3; ) 1 . C. (3;− ) 1 . D. ( 3 − ;− ) 1 .  2 
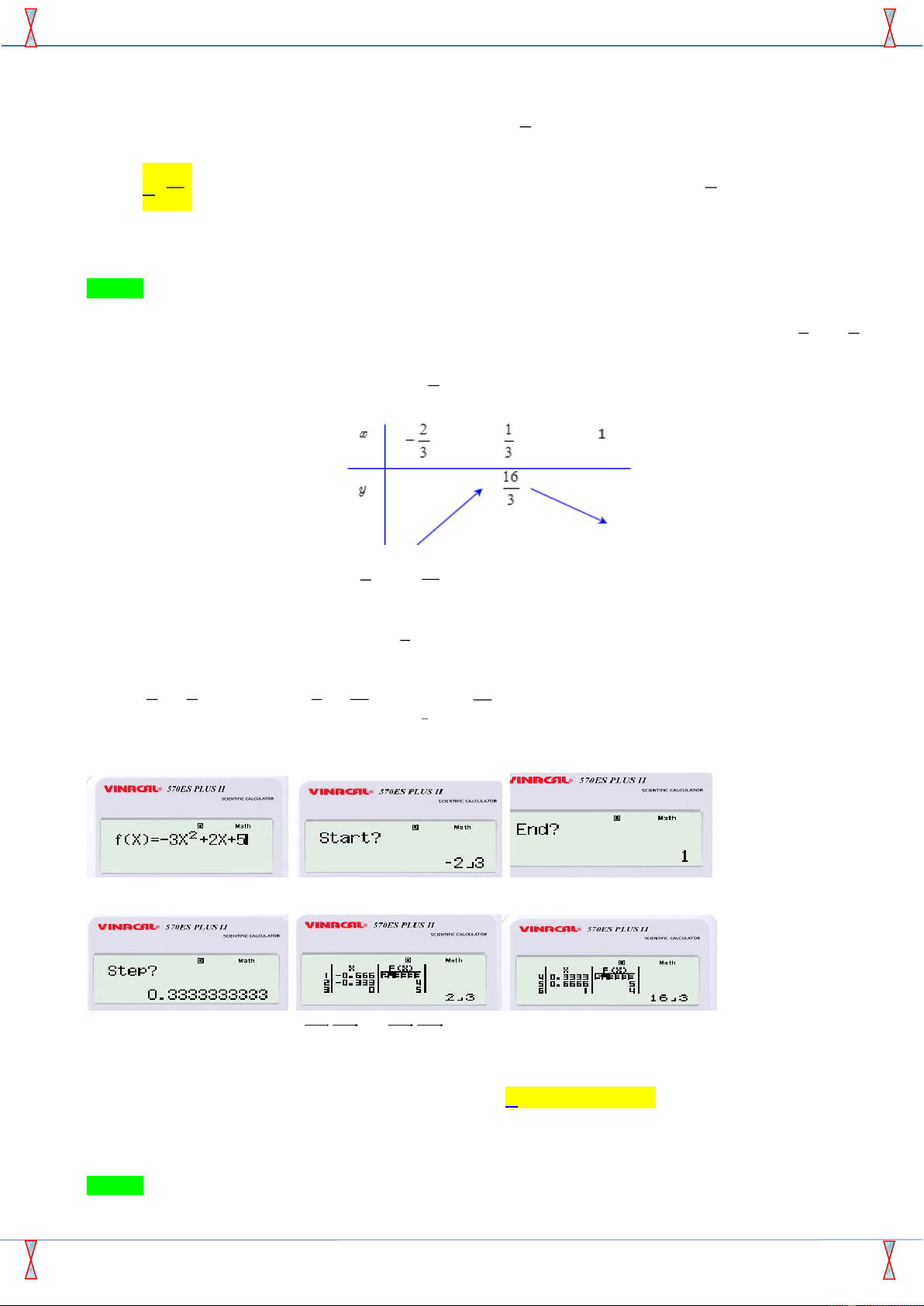
Câu 33: Giá trị lớn nhất của hàm số 2 y = 3
− x + 2x + 5 trên − ;1   là  3  16 7 A. . B. 5 . C. 1. D. . 3 3
Câu 34: Cho tam giác ABC có A . B BC = −B .
C AC . Tam giác ABC có tính chất gì? A. ABC  vuông tại A . B. ABC  cân tại B . C. ABC  vuông tại B . D. ABC  cân tại A . uuur uuur
Câu 35: Cho tam giác ABC có AB =10, AC =17 , BC =15 . Tính A . B AC . A. 164. B. 164 − . C. 82 − . D. 82 . 4 − x + x + 2
Câu 36: Tập xác định của hàm số y = 2 x − x − là 12 A.  2 − ;  4 . B. ( 3 − ; 2 − )( 2 − ;4) . C. ( 2 − ;4) . D.  2 − ;4).
Câu 37: Tìm giá trị của tham số m để đỉnh I của đồ thị hàm số 2
y = −x + 6x + m thuộc đường thẳng y = x + 2019 . A. m = 2020 . B. m = 2000 . C. m = 2036 . D. m = 2013.
Câu 38: Cho tam giác ABC vuông cân tại A có BC = a 2 . Tính độ dài BA + BC . A. 2a 5 . B. a 5 . C. a 3 . D. 2a 3 .
Câu 39: Biết đường thẳng d : y = −x + 4 cắt parabol (P) 2
: y = x − 2x tại hai điểm phân biệt A và B . Tìm tọa
độ trọng tâm G của tam giác OAB .  1 7  A. G ;   . B. G (1; 2 − ) .  3 3  1− 17 9 − 17   1 7  C. G  ;    . D. G ;   . 3 3    2 2 
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 4
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
mx + 2y = m +1
Câu 40: Cho hệ phương trình 
với m là tham số thực. Tìm tất cả các giá trị của m để hệ
2x + my = 2m −1
phương trình đã cho vô nghiệm. A. m = 2. − B. m  2. − C. m  2. D. m = 2. x 6
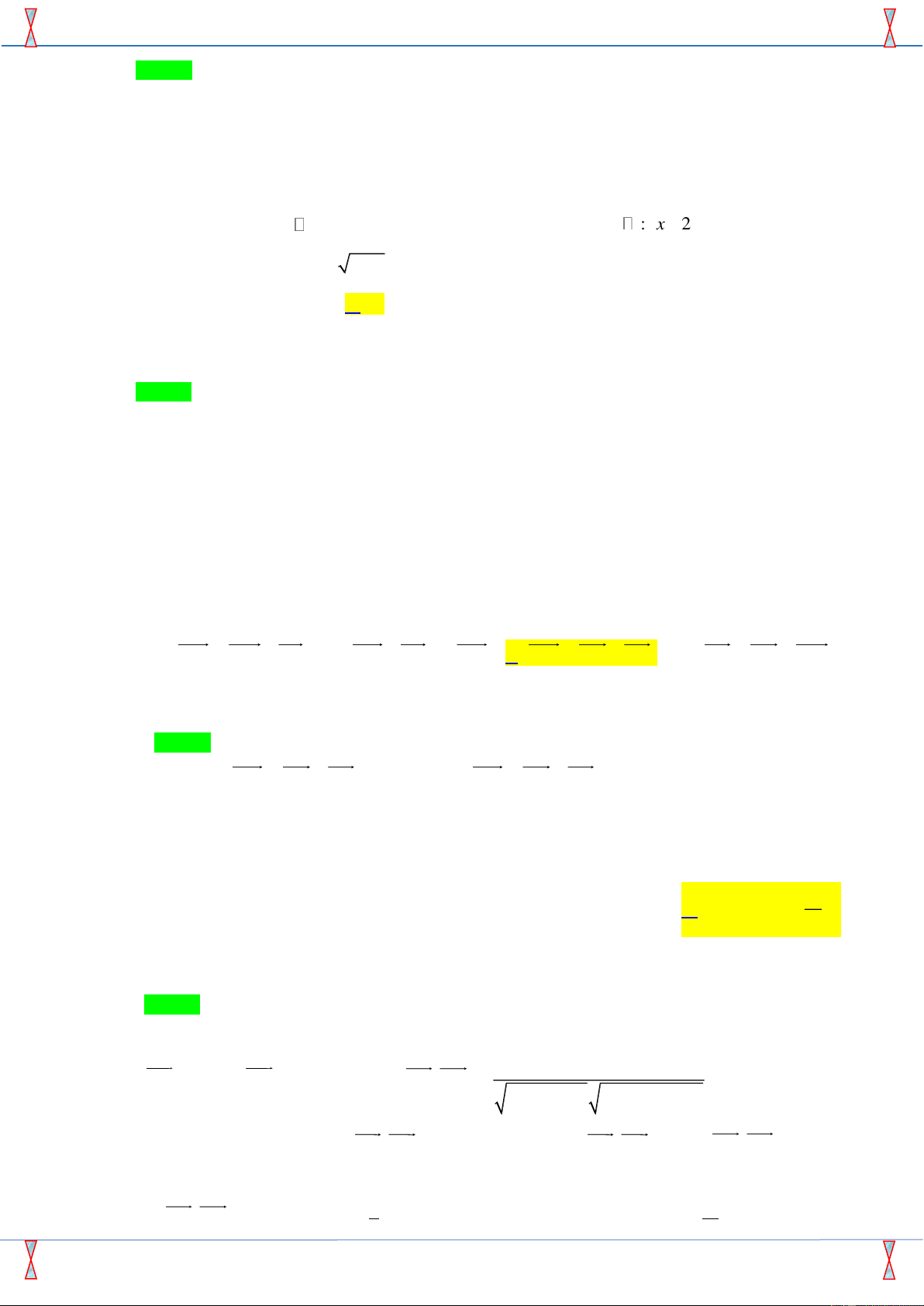
Câu 41: Giá trị nhỏ nhất của hàm số f (x) = +
với x  2 là số có dạng a 3 + b ( a, b là các số nguyên). 2 x − 2 Tính 2 2 a + b . A. 5. B. 6. C. 3. D. 4. (x − 2)(mx + ) 1
Câu 42: Số các giá trị thực của tham số m để phương trình
= 0 có nghiệm duy nhất là x +1 A. 3 . B. 2 . C. 0 . D. 1.
Câu 43: Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x − 2x +1 = m có hai nghiệm phân biệt. A. m  0 . B. m  0 .
C. m 1 hoặc m = 0 . D. 0  m 1.
Câu 44: Tìm tất cả các giá trị thực của tham số m để phương trình 3 2
x − mx − x + m = 0 có ba nghiệm thực phân biệt. A. m  1 − . B. m  1  .
C. m  1 hoặc m = 0 . D. 0  m  1.
Câu 45: Cho phương trình 2
−x + mx + m +1 = 0 với m là tham số thực. Tính tổng S tất cả các giá trị thực
của tham số m để phương trình có hai nghiệm phân biệt x , x thỏa mãn x + x = 4. 1 2 1 2 A. S = 2 B. S = 2 − . C. S = 4 − D. S = 5.
Câu 46: Cho phương trình 2
x −10x + m = 2 − x . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho vô nghiệm.
A. 16  m  20 . B. 3 −  m 16 C. m . D. m  16.
Câu 47: Tập tất cả các giá trị của tham số m để phương trình 2 2
x + 1− x = m có tập nghiệm là  ; a b . Tính
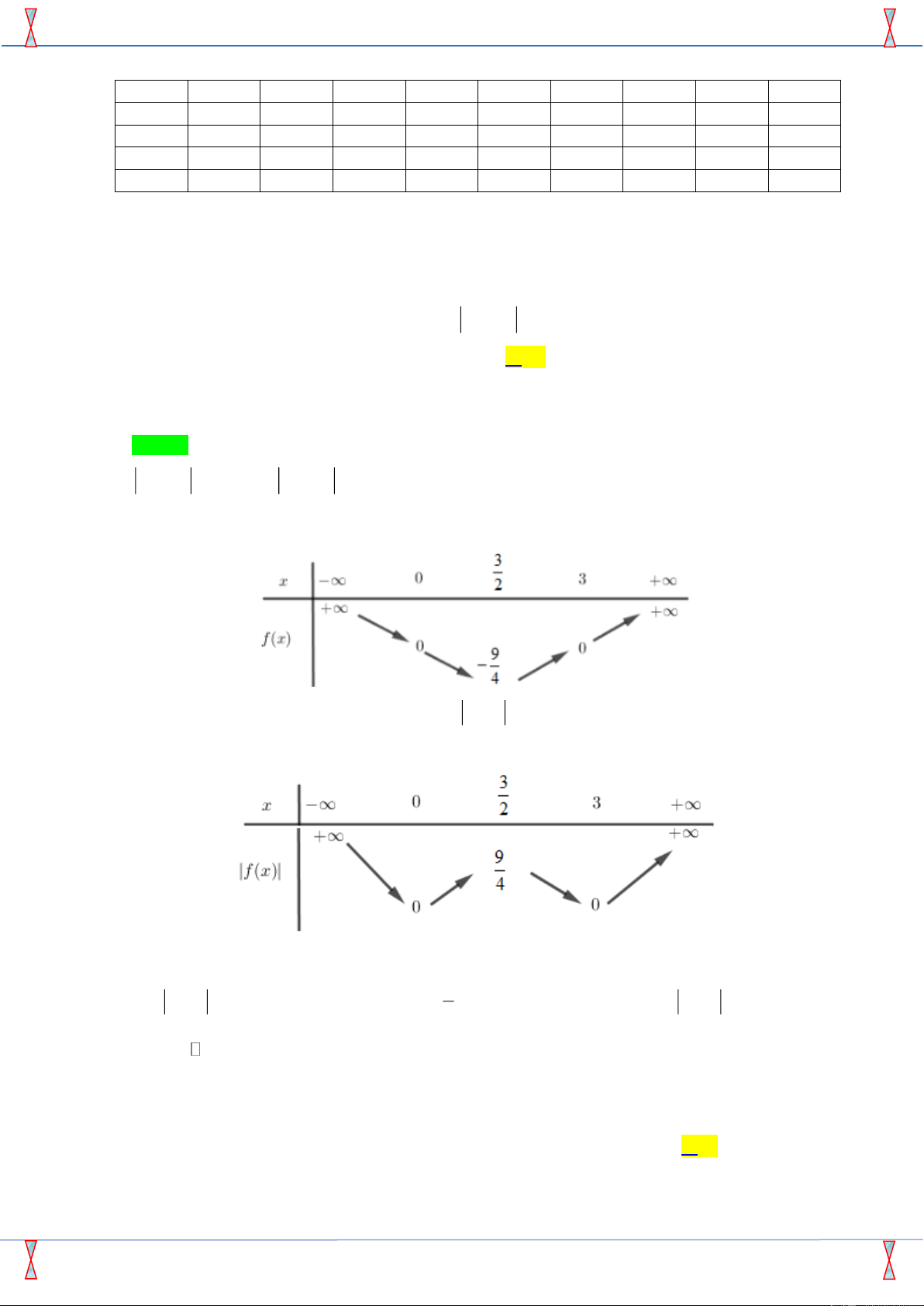
S = a + b ? 9 1 A. 0. B. . C. 1. D. . 4 4 Câu 48: Cho hàm số 2
y = x − 2 x có đồ thị như hình vẽ. Gọi S là tập các giá trị nguyên của m đề phương trình 2
x − 2 x + m = 1 có hai nghiệm phân biệt. Tính tổng các phần tử của tập S . A. 1 − . B. 2 . C. 4 . D. 0 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 5
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Câu 49: Trong hệ tọa độ Oxy cho ba điểm A(1; 4
− ) , B(4;5) và C(0; 9
− ) . Điểm M di chuyển trên trục Ox
. Đặt Q = 2 MA + 2MB + 3 MB + MC . Biết giá trị nhỏ nhất của Q có dạng a b trong đó a , b là
các số nguyên dương và a , b  20 . Tính a − b . A. 15 − . B. 17 − . C. 14 − . D. −11.
Câu 50: Cho x, y thoả mãn 2 2
x + y = a . Xác định a , biết rằng giá trị lớn nhất của P = 2x + 3y với x, y  0 là 117 . A. a = 9 . B. a = 13 . C. a = 5 .
D. a = 3 3 .
---------- HẾT ----------
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 6
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.B 5.C 6.D 7.C 8.A 9.A 10.D 11.A 12.C 13.B 14.A 15.D 16.B 17.C 18.D 19.C 20.B 21.B 22.C 23.A 24.C 25.C 26.C 27.B 28.B 29.A 30.C 31.C 32.B 33.A 34.D 35.D 36.D 37.D 38.B 39.A 40.A 41.A 42.A 43.C 44.B 45.B 46.D 47.B 48.B 49.D 50.A
GIẢI CHI TIẾT ĐỀ HỌC KỲ I LỚP 10 MÔN TOÁN
THPT LƯƠNG THẾ VINH-HÀ NỘI NĂM HỌC 2019 - 2020 Câu 1.
Số các giá trị nguyên của m để phương trình 2
x − 3x − m = 0 có bốn nghiệm phân biệt là A. vô số. B. 0 . C. 2 . D. 4 . Lời giải.
Tác giả: Mai Quỳnh Vân ; Fb: Vân Mai Chọn C 2 2
x − 3x − m = 0  x − 3x = m (*)
Xét hàm số f ( x) 2
= x −3x, ta có bảng biến thiên của hàm số y = f (x) như sau:
Từ đó ta suy ra bảng biến thiên của hàm số y = f ( x) như sau:
Yêu cầu bài toán  phương trình (*) có 4 nghiệm phân biệt  đường thẳng y = m cắt đồ thị hàm số 9
y = f ( x) tại 4 điểm phân biệt  0  m
(dựa vào BBT của hàm số y = f ( x) ). 4 Do m  nên m 1;  2 . Câu 2. Cho parabol (P) 2
: y = ax + bx + 4 đi qua điểm A(1;7) và có trục đối xứng x = 1
− . Tích ab nhận giá trị bằng A. 6 − . B. 4 . C. 18 − . D. 2 . Lời giải
Tác giả: Nguyễn Thị Xuyến; Fb: Nguyen Xuyen
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 7
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Chọn D Đồ thị hàm số 2
y = ax + bx + c là parabol nên a  0 .
Parabol đi qua điểm A(1;7) nên ta có 2 7 = .1 a + .1
b + 4  a + b = 3 . b −
Trục đối xứng của parabol là đường thẳng x = 1 − nên = 1
−  b = 2a . 2aa + b = 3 a = 1 Vậy ta có hệ:     ab = 1.2 = 2. 2a − b = 0 b  = 2 x − 2y = 2 − Câu 3.
Nghiệm của hệ phương trình  là 2x + 3y = 10
A. ( x; y) = (2;2) .
B. ( x; y) = (3;6) .
C. ( x; y) = ( 2
− ;− 2) . D. (x; y) = (1;− 2) . Lời giải.
Tác giả: Trần Thanh Hà ; Fb: Hà Trần
Phản biện: Đồng Anh Tú; FB: Anh Tú Chọn A x − 2y = 2 − x = 2y − 2  x = 2y − 2 x = 2 Ta có:        . 2x + 3y =10 2
 (2y − 2) + 3y =10 7 y =14 y = 2
Vậy hệ phương trình đã cho có nghiệm là: ( x; y) = (2;2) . Câu 4.
Cho đoạn thẳng AB = 6. Tập hợp các điểm M thỏa mãn 2 2
MA + MB = 18 là
A. một đoạn thẳng. B. một điểm.
C. một đường tròn.
D. một đường thẳng. Lời giải
Tác giả: Trần kim Nhung ; Fb:Nhung trần thị Kim Chọn B
Gọi I là trung điểm của AB IA + IB = 0 và IA = IB = 3.
Giả sử M là điểm thỏa mãn bài toán. 2 2 Ta có: 2 2
MA + MB = 18  MA + MB = 18 2 2
 (MI + IA) + (MI + IB) =18 2 2 2
 2MI + 2MI.(IA+ IB) + IA + IB =18 2 2 2 2
 2MI + IA + IB =18  MI = 0.
Do đó: M trùng I .
Vậy tập hợp các điểm M thỏa mãn bài toán là một điểm. Câu 5.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC vuông tại A(2;2) . Biết C (4;− 2) và B Oy . Tìm tọa độ điểm B . A. B (0;3) . B. B (0; 3 − ) . C. B (0; ) 1 . D. B (0; − ) 1 . Lời giải
Tác giả: Trần Quang Đạt; Fb: Quang Đạt
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 8
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Chọn C
Do B Oy nên B có tọa độ (0; y) , y  . Khi đó AB = ( 2
− ; y − 2) AC = (2;− 4) ; .
Tam giác ABC vuông tại A nên A . B AC = 0  ( 2 − ).2+( y − 2).( 4 − ) = 0  y =1. Vậy B (0; ) 1 . Câu 6.
Lớp 10D có 37 học sinh, trong đó có 17 học sinh thích môn Văn, 19 học sinh thích môn Toán, 9 em
không thích môn nào. Số học sinh thích cả hai môn là A. 2 học sinh. B. 6 học sinh. C. 13 học sinh. D. 8 học sinh. Lời giải
Tác giả: Trịnh Duy Thanh; FB: Trịnh Duy Thanh Chọn D
Gọi số học sinh thích cả hai môn là x ( 0  x  17 ). Khi đó số học sinh chỉ thích môn Văn là 17 − x ,
số học sinh chỉ thích môn Toán là 19 − x .
Ta có: 9 + (17 − x) + (19 − x) + x = 37  x = 8. 4 − x 4 − x Câu 7. Phương trình =
có tất cả bao nhiêu nghiệm nguyên? x − 2 x − 2 A. 1. B. Vô số. C. 2 . D. 0 . Lời giải
Tác giả:Nguyễn Ngọc Hà ; Fb:Hangocnguyen Chọn C
Điều kiện xác định: x  2 .
Khi đó phương trình đã cho tương đương với 4 − x = 4 − x  4 − x  0  x  4 .
Kết hợp với điều kiện xác định ta có nghiệm của phương trình là 2  x  4 . Do x  nên x 3; 
4 . Vậy phương trình có 2 nghiệm nguyên. Câu 8.
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = x − 2 cắt parabol (P) 2
: y = x − mx + 2 tại đúng một điểm. m = 3 A.  . B. m = 3 . C. m = 5 − . D. m . m = 5 − Lời giải
Tác giả: Nguyễn Thị Hồng Hợp ; Fb: Nguyễn Thị Hồng Hợp Chọn A
Phương trình hoành độ giao điểm của đường thẳng d : y = x − 2 và pararabol (P) là: 2 2
x − 2 = x − mx + 2  x − (m + ) 1 x + 4 = 0 (1)
Đường thẳng d cắt parabol (P) tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép. Điều này tương đương với
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 9
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020  = (  = m + )2 m 3 2
1 − 4.4 = m + 2m −15 = 0   . m = 5 −
Câu 9. Cho các vectơ a , b có độ dài bằng 1 và 3a − 4b = 13 . Tính cos (a,b) . 1 1 3 A. . B. 1. C. . D. . 2 4 2 Lời giải
Tác giả: Nguyễn Thị Tỉnh ; Fb: Ngọc Tỉnh Chọn A
Ta có: 3a − 4b = 2
13  3a − 4b = 13  ( a − b)2 3 4 = 2 2 13  9a − 24 . a b +16b = 13. 2  a − a b c (a b) 2 9 24 os ,
+16 b =13  9.1− 24.1.1. o c s ( , a b) +16.1 =13 .  c (a b) 1 os , = . 2 Câu 10.
Cho tam giác ABC nhọn có BC = 3a và bán kính đường tròn ngoại tiếp tam giác ABC là R = a 3 . Tính số đo góc A . A. A =120 . B. A = 45 . C. A = 30 . D. A = 60 . Lời giải
Tác giả: Thân Thế Luân ; Fb: Luan Vu Chọn D BC BC 3a 3
Áp dụng định lý sin trong tam giác ABC , ta có = 2R  sin A = = = . sin A 2R 2a 3 2
Suy ra A = 60 (do tam giác ABC nhọn).
xy + x + y = 5
Câu 11: Số nghiệm của hệ phương trình  là 2 2 x + y = 5 A. 2 . B. 0 . C. 1. D. 3 . Lời giải
Tác giả: Đồng Anh Tú; Fb: Anh tu Chọn A
S = x + y Đặt  ( Điều kiện: 2 S  4P ) P = xy
Ta được hệ phương trình S + P = 5 P = 5 −  SP = 5 − S      2 S − 2P = 5 2 S − 2  (5− S) 2 = 5
S + 2S −15 = 0 S = 5 − S =  3  hoặc  .
P = 5 − S =10
P = 5 − S = 2 Với S = 5 − ; P =10 thì 2
S − 4P = 25 − 40 = 1
− 5  0 nên ta loại trường hợp này.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 10
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Với S = 5 − ; P =10 thì 2
S − 4P = 9 − 8 = 1  0 nên khi đó x, y là nghiệm của phương trình X =1 2
X − 3X + 2 = 0  X = 2
Ta có nghiệm hệ phương trình là ( ;
x y) = (1; 2) hoặc ( ; x y) = (2;1) . Câu 12.
Cho tam giác ABC là tam giác đều, O là tâm đường tròn ngoại tiếp tam giác ABC . Tìm mệnh đề đúng trong các mệnh đề sau.
A. OA + OB = OC .
B. OA + OB = 2OC .
C. OA + OB = CO .
D. OA + OB = 2CO . Lời giải
Tác giả: Thân Thế Luân; Fb: Luan Vu Chọn C Do ABC
đều nên O cũng là trọng tâm của ABC  .
Khi đó OA+ OB + OC = 0  OA+ OB = CO . Câu 13. Cho Parabol (P) 2
: y = −x + 2bx + c có điểm M (2;10) là điểm có tung độ lớn nhất. Tính giá trị của c . A. 22 . B. 6. C. 12. D. 10. Lời giải
Tác giả: Lê Văn Kỳ ; Fb: Lê Văn Kỳ
Chọn B
Từ đề bài suy ra a = 1. −
Ta có: điểm M (2;10) là điểm có tung độ lớn nhất  M (2;10) là tọa độ đỉnh của (P) .  2 − b 2 = b  = 2 b  = 2   2 −     .   = − + +  = M ( b c c 2;10)   (P) 2 10 2 4 6
Câu 14. Trong các hàm số sau đâu là hàm số bậc nhất?
A. y = ( − x)( + x) 2 1 1 + x + 2 . x B. y = ( − )2 1 2 1 x − . x 6 + 2x C. 2 y = 1− x . D. y = . x Lời giải
Tác giả: Lê Văn Kỳ ; Fb: Lê Văn Kỳ Chọn A
Ta có y = ( − x)( + x) 2 2 2 1 1
+ x + 2x =1− x + x + 2x = 2x +1 là hàm số bậc nhất.
Câu 15. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A.   : 3n nn + 3 .
B.1  2  6  7 .
C. 6  4 10  7 . D. x   (x − )2 2 : 2  x . Lời giải
Tác giả: Lê Thị Phương; Fb: Plus kính gửi
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 11
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Chọn D
• Với n =1 thì 3n = 3;n + 3 = 4 nên đáp án A là đúng.
• Ta có mệnh đề P :"1 2" và mệnh đề Q :"6  7" là mệnh đề sai nên mệnh đề P Q hay mệnh
đề 1 2  6  7 là mệnh đề đúng. Đáp án B đúng.
• Ta có mệnh đề P :"6  4" là mệnh đề sai và mệnh đề Q :"10  7" là mệnh đề đúng nên mệnh đề
P Q hay mệnh đề 6  4 10  7 là mệnh đề đúng. Đáp án C đúng. • Với x = 1 −  thì (x − )2 2 = 9 ; 2 x = 1 nên mệnh đề x   (x − )2 2 : 2
x là mệnh đề sai.
Câu 16. Số nghiệm của phương trình − x ( 2 3
x − 9x + 20) = 0 là: A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Tác giả: Trần Văn Trưởng; FB: Trần Văn Trưởng Chọn B
Điều kiện xác định: x  3. x = 3 3− x = 0 
Khi đó phương trình    x = 4 (loại) .  2
x − 9x + 20 = 0 x =  5 (loại)
Vậy phương trình đã cho có 1 nghiệm.
Câu 17. Cho ba điểm bất kỳ M , N , P . Đẳng thức nào sau đây sai?
A. PM = NM − NP . B. MN + NP = −PM . C. MN = MP − PN .
D. NP = MP + NM . Lời giải
Tác giả: Lê Xuân Sơn; Fb: Lê Xuân Sơn Chọn C
Đẳng thức MN = MP − PN sai. (Đẳng thức MN = MP − PN chỉ đúng trong trường hợp đặc biệt P N ).
Câu 18. Trong mặt phẳng tọa độ Oxy , cho A(1; ) 3 ; B( 1 − ; 8
− ). Tìm điều kiện của a để điểm M ( ;0
a ) thỏa mãn góc AMB là một góc tù.   A. a  5 − ;  5 .
B. a (5; +) . C. a (− ;  5 − ) . D. a  (− ) 5 5;5 \  . 11   Lời giải
Tác giả và giải: Nguyễn Văn Bình ; Fb: Nguyễn Văn Bình Chọn D Ta có: 1− a 1 − − a − 24 MA(1− ; a 3); MB( 1 − − ; a 8 − ); cos(M ; A MB) ( )( ) = . (1− a)2 +9 ( 1 − − a)2 + 64
Góc AMB là một góc tù  (M ;
A MB) là một góc tù  cos(M ;
A MB)  0 và M ; A MB không ngược hướng. 8 5 +) M ;
A MB cùng phương  − (1− a) = 1 − − a  8 − + 8a = 3
− − 3a a = 3 11
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 12
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020  6   16 −  5 Khi đó MA ;3 ; MB ; 8 −     nên M ;
A MB ngược hướng. Do đó a  (1) 11   11  11 (1− a)( 1 − − a) − 24 +) cos (M ; A MB)  0 2 
 0  a − 25  0  5 −  a  5 (2) (1− a)2 +9. ( 1 − − a)2 + 64  
Từ (1) và (2), a  (− ) 5 5;5 \   . 11  
Câu này ở đáp D nguyên văn trong đề gốc là: D. a ( 5 − ;5).  
Chúng tôi nghĩ đề ra sai và đã sửa lại thành D. a (− ) 5 5;5 \  . 11  
Câu 19: Một học sinh giải phương trình 2
2x + 4 = 2x (*) như sau:
Bước 1: Điều kiện xác định là ¡ . Bước 2: (*) 2 2 Û 2x + 4 = 4x Bước 3: 2
Û x = 2 . Vậy phương trình có nghiệm x = 2 và x = - 2
Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào? A. Lời giải đúng.
B. Lời giải sai từ bước 1.
C. Lời giải sai từ bước 2.
D. Lời giải sai từ bước 3. Lời giải
Tác giả: Trần Thị Thủy; Fb: Thủy Trần Chọn C ìï 2x ³ 0 ìï x ³ 0 ìï x ³ 0 2 ï ï ï
2x + 4 = 2x Û í Û í Û í Û x = 2 . 2 2 2 ï 2x + 4 = 4x ï x = 2 ï ïî ïî ï x = ± 2 î Chọn C.
Câu 20. Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng? x −1 A. 3
y = x + 3x .
B. y = x + 3 + x − 3 .
C. y = ( x + )2 1 . D. y = . x Lời giải
Tác giả :Trần Thị Phượng Uyên, FB: UyenTran Chọn B
Đồ thị hàm số nhận trục tung làm trục đối xứng khi hàm số là hàm chẵn
Xét hàm số y = x + 3 + x − 3 , ta có:
f (−x) = −x + 3 + −x − 3 = x − 3 + x + 3 = f ( x)
Suy ra hàm số trên là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
Câu 21. Phương trình 2 2
x − 7x + 6 = x − 2x + 4 có bao nhiêu nghiệm nguyên âm? A. 2. B. 0. C. 1. D. 3. Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 13
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Tác giả : Chu Quốc Hùng, FB: Chu Quốc Hùng Edu Chọn B  2 x = 2   2 2 5
x − 7x + 6 = x − 2x + 4 x =  2 2 
Ta có: x − 7x + 6 = x − 2x + 4    5  x = 2  2 2 
x − 7x + 6 = −x + 2x − 4 . 2
2x −9x +10 = 0  5 x =  2
Vậy phương trình không có nghiệm nguyên âm.
Câu 22. Có bao nhiêu giá trị của tham số m để hai đường thẳng d : y = m −1 x + 3m − 2 và 1 ( ) d : y = ( 2
m −1 x + 2m −1 song song với nhau ? 2 ) A. 3 . B. 2 . C. 1. D. 0 . Lời giải: Chọn C.
d : y = m −1 x + 3m − 2 có hệ số a = m −1, b = 3m − 2 1 ( ) 1 1 d : y = ( 2
m −1 x + 2m −1 có hệ số 2
a = m −1 , b = 2m −1 2 ) 2 1 m = 0 a = a 2
m −1 = m −1  d 1 2 và d song song    
 m =1  m = 0. 1 2 b b  3
m − 2  2m −1 1 2  m  1
Câu 23. Cho tam giác ABC có AB = 4cm ; AC =12cm và góc BAC = 120 . Tính diện tích tam giác ABC . A. 12 3 ( 2 cm ). B. 24 3 ( 2 cm ). C. 12 ( 2 cm ). D. 24 ( 2 cm ). Lời giải Chọn A 1 1
Diện tích tam giác ABC là S = . AB AC.sin BAC = .4.12.sin120 = 12 3 ( 2 cm ) 2 2
Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của a? 1
A. a  3a . B. 2 2 a  −2a .
C. 2 − a  3− a . D. a  −a . 3 Lời giải Chọn C
A. a  3a  2a  0  a  0 B. 2 2 2 a  2
− a  3a  0  a  0
C. 2 − a  3− a  2  3 (luôn đúng với mọi a). 1 4 D. a  −a
a  0  a  0 3 3
Câu 25. Cho tam giác ABC thỏa mãn 2 2 2
BC + AC − AB − 2B .
C AC = 0 . Khi đó, góc C có số đo là A. C = 150 .
B. C = 60 . C. C = 45 . D. C = 30 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 14
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Lời giải
Tác giả:ThanhLoan ; Fb: ThanhLoan Chọn C Theo đề ra ta có: 2 2 2
BC + AC − AB − 2B . C AC = 0 2 2 2
BC + AC − AB = 2B . C AC 2 2 2
BC + AC − AB  = 2 BC.AC  2cosC − 2 = 2 0  cos C =  C = 45 . 2
Câu 26. Cho hình bình hành ABCD có AB = 1, AD = 2, DAB = 60 . Tính độ dài cạnh AC . 7 A. 3 . B. . C. 7 . D. 5 . 3 Lời giải
Tác giả: Nguyễn Thị Huệ ; Fb: Nguyễn Thị Huệ Chọn C
Gọi O là tâm của hình bình hành ABCD . Xét tam giác ABD , áp dụng định lý cosin ta có, 1 2 2 2
BD = AB + AD − 2.A . B A .
D cos 60 = 1+ 4 − 2.1.2. = 3. 2
Mặt khác , áp dụng công thức tính độ dài đường trung tuyến AO trong tam giác ABD , ta có, 2 2 2 AB + AD BD 1+ 4 3 7 7 2 AO = − = − = . Suy ra AO =
AC = 2AO = 7 . 2 4 2 4 4 2 Vậy AC = 7 . Câu 27. Cho hàm số 2
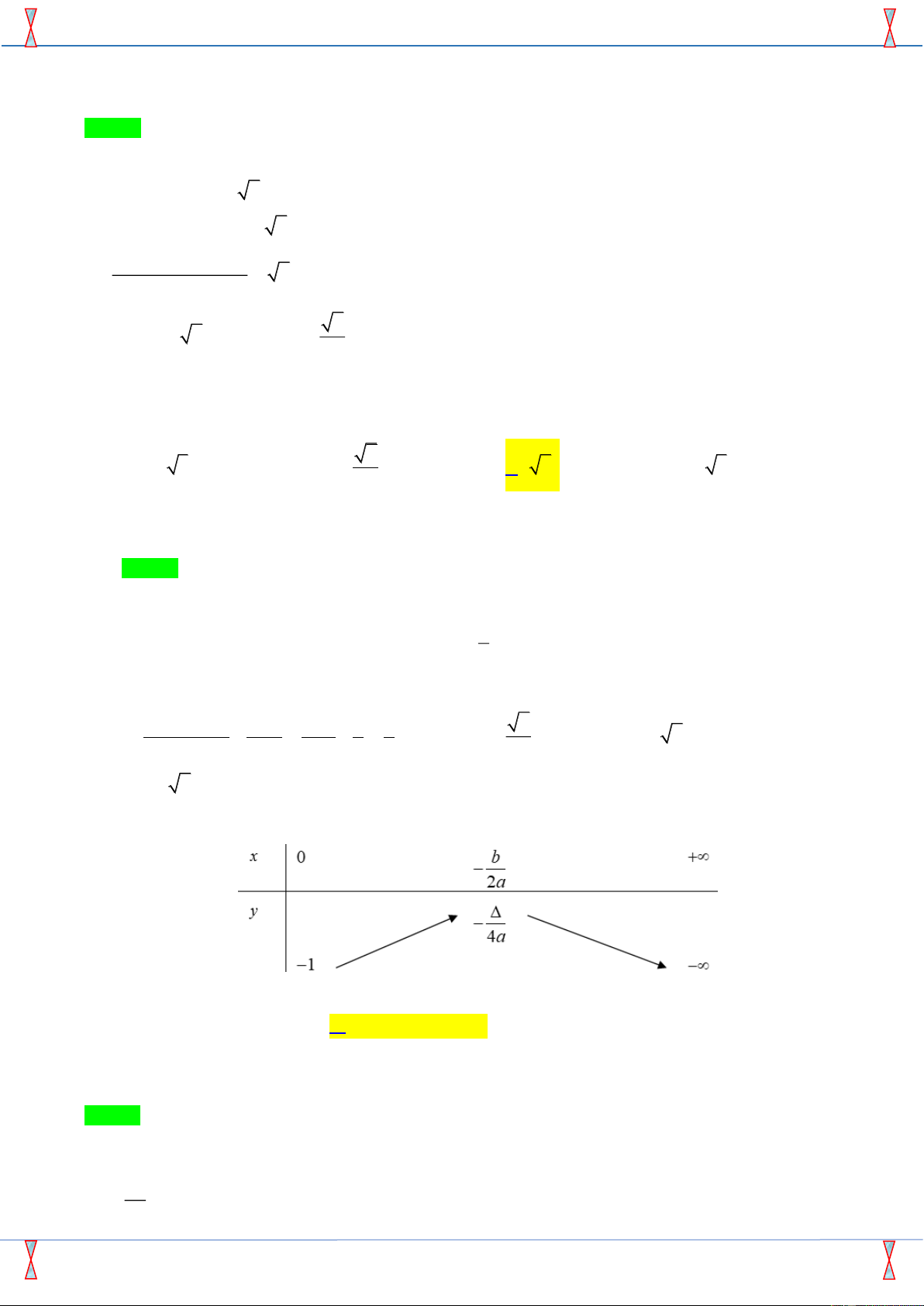
y = ax + bx + c (a  0) có bảng biến thiên như hình vẽ dưới đây
Xác định dấu của a,b, c
A. a  0, b  0, c  0 .
B. a  0, b  0, c  0 . C. a  0, b  0, c  0
D. a  0, b  0, c  0 . Lời giải
Tác giả:Huỳnh Hữu Hùng ; Fb:Huuhung Huynh Chọn B
Từ bảng biến thiên ta thấy đồ thị hàm số có bề lõm quay xuống nên a  0 . b Vì −  0 nên b  0. 2a
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 15
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Giao điểm của đồ thị hàm số với trục Oy là điểm (0; 1 − ) nên c = 1 −  0 . Câu 28. Cho hàm số 2
y = f (x) = x − 4x + 2 trong các mệnh đề dưới đây mệnh đề nào đúng ? A. f ( 2019 − )  f ( 2019 2 −3 ) .
B. f ( 2019 )  f ( 2019 2 3 ) .
C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
D. Đồ thị hàm số nhận đường thẳng x = 2 − làm trục đối xứng. Lời giải
Tác giả:Huỳnh Hữu Hùng ; Fb:Huuhung Huynh Chọn B b
+) Hàm số đã cho là hàm số bậc 2 chỉ có đúng một trục đối xứng là đường thẳng x = − = 2 làm trục đối xứng 2aD sai. +) f (2) = 2 −  0  C sai. b
+) Hệ số a = 1  0 và −
= 2 nên hàm số đồng biến trên khoảng (2;+) , nghịch biến trên khoảng (−;2) . Từ 2a đó, vì 2019 2019 2  2 −  3 − nên f ( 2019 − )  f ( 2019 2 3 − ) A sai. Ta cũng có 2019 2019 3  2  2 nên 2019 2019 f (2 )  f (3 )  B đúng.
Câu 29. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(5; ) 3 , B(2;− ) 1 , C ( 1
− ;5). Tìm tọa độ điểm H là
trực tâm tam giác ABC .  7   7  A. H (3; 2) . B. H (3; 2 − ). C. H 2;   . D. H 2; − −   .  3   3  Lời giải
Tác giả: Hà Minh Yên ; Fb:Hà Minh Yên Chọn A A H C B AH.BC = 0 Gọi H ( ;
x y) là trực tâm của tam giác ABC . Khi đó  (*). BH.AC = 0
AH = ( x − 5; y − 3); BC = ( 3
− ;6) ; BH = (x − 2; y + ) 1 ; AC = ( 6 − ;2).  3 −
 ( x − 5) + 6( y − 3) = 0 x − 2y = 1 − x = 3 (*)       .  6 −
 ( x − 2) + 2( y + ) 1 = 0 3  x − y = 7 y = 2 Vậy : H (3; 2) .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 16
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Câu 30. Tổng các nghiệm của phương trình ( − ) 4 2 3
2 x − 4x − ( 3 − 2) = 0 là 4 2 A. −1. B. . C. 0 . D. . 3 − 2 3 − 2 Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn C Đặt 2
t = x , điều kiện: t  0 . Khi đó phương trình ( − ) 4 2 3
2 x − 4x − ( 3 − 2) = 0 ( ) 1 trở thành: ( − ) 2 3
2 t − 4t − ( 3 − 2) = 0 ( ) * .
Nhận thấy phương trình ( ) * có a c = − ( − )2 . 3 2  0 nên phương trình ( )
* có hai nghiệm phân biệt: t  0 (loại) 1 , t  0 (nhận). 2 Suy ra phương trình ( )
1 có 2 nghiệm là: x = − t , x = t . 1 2 2 2
Vậy x + x = − t + t = 0 . 1 2 2 2
Câu 31. Cho a, b là hai số thực tùy ý. Mệnh đề nào sau đây đúng? A. Nếu 2 2
a b thì a b .
B. Nếu a b thì 2 2 a b .
C. Nếu a b và a  0 thì 2 2 a b .
D. Nếu a b và b  0 thì 2 2 a b . Lời giải
Tác giả: Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn C
Đáp án A sai với a = 2 − , b = 1 − .
Đáp án B sai với a = 1 − , b = 0 . a b
Đáp án C đúng vì 2 2 
 0  a b a b . a  0
Đáp án D sai với a = 1 − , b =1.
Câu 32. Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có A(1; 2) , B ( 2 − ;4) , C(0; ) 3 . Tìm tọa độ điểm D . A. ( 3 − ; ) 1 . B. (3; ) 1 . C. (3; − ) 1 . D. ( 3 − ;− ) 1 . Lời giải
Tác giả: Phạm Văn Tuân; Fb: mr.vtuan. Chọn B
Vì ABCD là hình bình hành nên AB = DC . Ta có: AB = ( 3
− ;2) ; DC = (−x ;3− y . D D ) −x = 3 − x = 3 D D
Do AB = DC , suy ra    . 3 − y = 2 y = 1   D D
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 17
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Vậy tọa độ điểm D là (3; ) 1 .  2 
Câu 33. Giá trị lớn nhất của hàm số 2 y = 3
− x + 2x + 5 trên − ;1   là  3  16 7 A. . B. 5 . C. 1. D. . 3 3 Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh Chọn A 1  2  Cách 1: Hàm số 2 y = 3
− x + 2x + 5 là hàm số bậc hai có hệ số a = 3
−  0 và hoành độ đỉnh là x =  − ;1 . I   3  3   2 
Bảng biến thiên của hàm số trên đoạn − ;1   là:  3   2  16
Vậy giá trị lớn nhất của hàm số trên − ;1   là .  3  3 1
Cách 2: Ta có: y = 6
− x + 2 ; y = 0  x = . 3  2  7  1  16 16 Vì y − =   ; y ( ) 1 = 4 ; y =   nên max y = .  3  3  3  3  2  − ;1 3    3 
Cách 3: Sử dụng chức năng MODE 7:
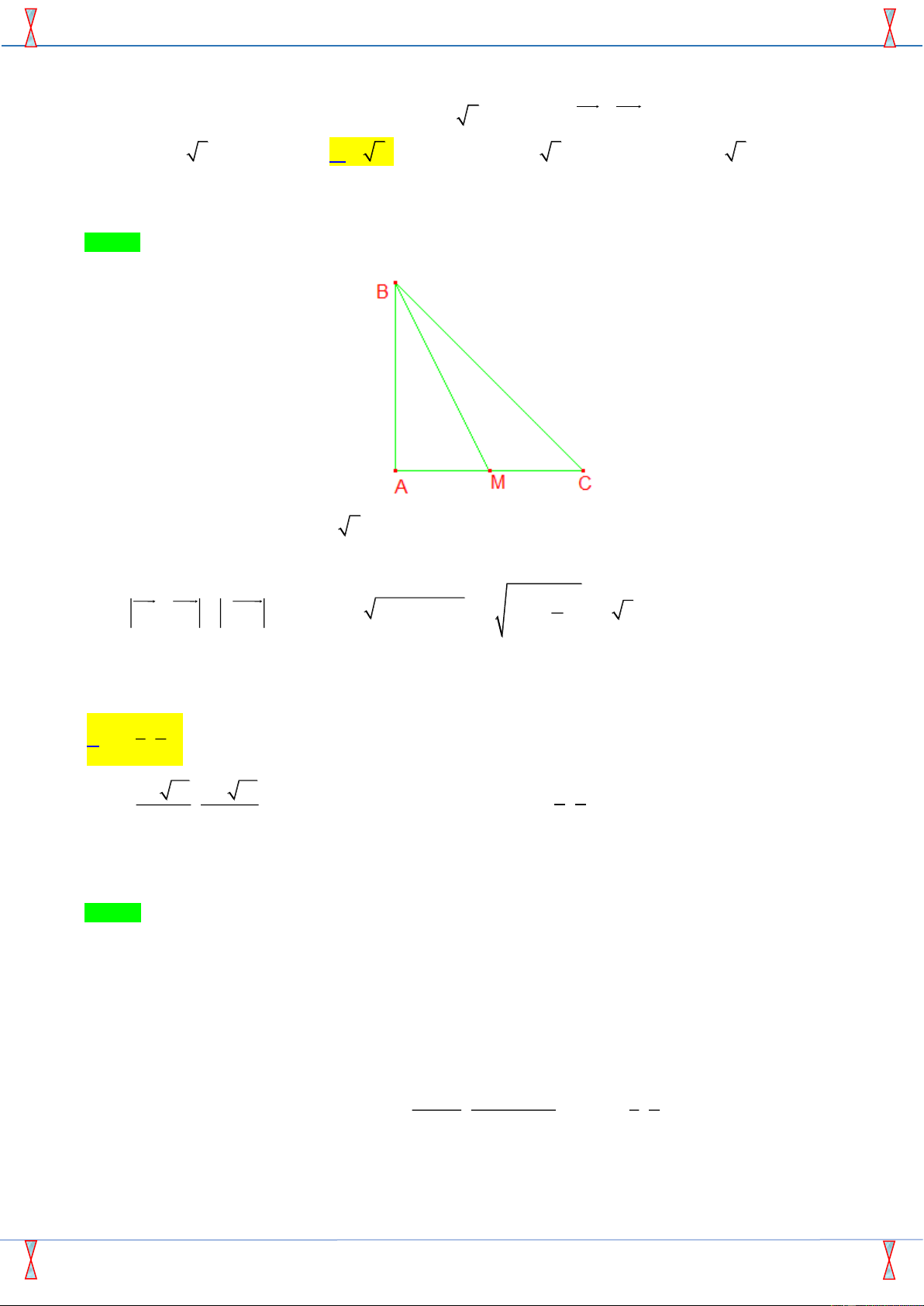
Câu 34. Cho tam giác ABC có A . B BC = −B .
C AC . Tam giác ABC có tính chất gì? A. ABC  vuông tại A . B. ABC  cân tại B . C. ABC  vuông tại B . D. ABC  cân tại A . Lời giải
Tác giả: Lê Thanh Hùng; Fb: Hung Le Thanh Chọn D Cách 1:
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 18
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Gọi M là trung điểm của BC AB + AC = 2AM . Ta có: A .
B BC = −BC.AC BC.( AB + AC) = 0  B .
C 2AM = 0  BC ⊥ AM . Vậy ABC  cân tại A . Cách 2: Ta có: A . B BC = −B . C AC  −B . A BC = C − . B CA B . A B .
C cos B = C . B C .
A cosC A .
B cos B = A . C cosC 2 2 2 2 2 2
BC + BA − AC
CA + CB − ABA . B = AC. 2.BC.BA 2.C . A CB 2 2 2 2 2 2
BC + BA − AC = CA + CB − AB 2 2
 2AB = 2.AC AB = AC Vậy ABC  cân tại A . uuur uuur
Câu 35. Cho tam giác ABC có AB =10 , AC = 17 , BC =15 . Tính A . B AC . A. 164 . B. 164 − . C. 82 − . D. 82 . Lời giải
Tác giả:Trần Minh; Fb: Tran Minh Chọn D 2 2 2 Ta có: 2
BC = BC = ( AC − AB)2 = AB − 2A . B AC + AC 2 2 = AB − 2A . B AC + AC 2 2 2 uuur uuur
AB + AC − BC 2 2 2 uuur uuur 10 +17 −15 Vậy A . B AC =  A . B AC = = 82 . 2 2 4 − x + x + 2
Câu 36. Tập xác định của hàm số y = 2 x − x − là 12 A.  2 − ;  4 . B. ( 3 − ; 2 − )( 2 − ;4) . C. ( 2 − ;4) . D.  2 − ;4). Lời giải
Tác giả: Bùi Văn Khánh; Fb:Khánh Bùi Văn Chọn D x  4 4 − x  0   x  2 − ĐKXĐ: x + 2  0    2 −  x  4 . x  3 −   2
x − x −12  0 x  4
Vậy, tập xác định của hàm số là D =  2 − ;4).
Câu 37. Tìm giá trị của tham số m để đỉnh I của đồ thị hàm số 2
y = −x + 6x + m thuộc đường thẳng y = x + 2019 . A. m = 2020 . B. m = 2000 . C. m = 2036 . D. m = 2013. Lời giải
Tác giả: Bùi Văn Khánh ; Fb:Khánh Bùi Văn Chọn D Đồ thị hàm số 2
y = −x + 6x + m là parabol có đỉnh I (3;9 + m) .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 19
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Đỉnh I (3;9 + m) thuộc đường thẳng y = x + 2019  9 + m = 3+ 2019  m = 2013.
Câu 38. Cho tam giác ABC vuông cân tại A có BC = a 2 . Tính độ dài BA + BC . A. 2a 5 . B. a 5 . C. a 3 . D. 2a 3 . Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ Chọn B ABC
vuông cân tại A có BC = a 2 nên AB = AC = a
Gọi M là trung điểm AC 2  a
Ta có BA + BC = 2BM = 2BM 2 2 = 2 AB + AM 2 = 2 a + = a 5    2 
Câu 39. Biết đường thẳng d : y = −x + 4 cắt parabol (P) 2
: y = x − 2x tại hai điểm phân biệt A và B . Tìm tọa độ
trọng tâm G của tam giác OAB .  1 7  A. G ;   . B. G (1; 2 − ) .  3 3  1− 17 9 − 17   1 7  C. G  ;    . D. G ;   . 3 3    2 2  Lời giải
Tác giả: Ngô Thị Thơ ; Fb: Ngô Thị Thơ Chọn A
Xét phương trình hoành độ giao điểm của d và (P) : 2
x − 2x = −x + 4 2
x − x − 4 = 0( ) * ( )
* có hai nghiệm phân biệt x ; x thỏa mãn: x + x = 1. Khi đó giao điểm của d và ( P) lần lượt là 1 2 1 2
A( x ;−x + 4 , B x ;−x + 4 1 1 ) ( 2 2 )
x + x −x − x + 8   1 7 
Tọa độ trọng tâm G của tam giác OAB là 1 2 1 2 G ;   hay G ;    3 3   3 3 
mx + 2y = m +1
Câu 40. Cho hệ phương trình 
với m là tham số thực. Tìm tất cả các giá trị của m để hệ phương
2x + my = 2m −1 trình đã cho vô nghiệm.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 20
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 A. m = 2. − B. m  2. − C. m  2. D. m = 2. Lời giải
Tác giả: Tạ Tiến Thanh ; Fb: Thanh Ta
Chọn A Ta có các định thức 2 2 2
D = m − 4; D = m − 3m + 2; D = 2m − 3m − 2 . x ym = 2
Hệ vô nghiệm thì D = 0  m = 2 −
+ Khi m = 2 : D = 0; D = 0.( Hệ vô số nghiệm). x y + Khi m = 2
− : D =12; D =12.( Hệ vô nghiệm). x y x 6
Câu 41. Giá trị nhỏ nhất của hàm số f (x) = + x
là số có dạng a 3 + b ( a, b là các số nguyên). 2 x − với 2 2 Tính 2 2 a + b . A. 5. B. 6. C. 3. D. 4. Lời giải
Tác giả: Tạ Tiên Thanh ; Fb: Thanh Ta Chọn A x 6 x − 2 6 x − 2 6
Với x  2 thì x − 2  0 nên f (x) = + = + +1 2 . +1= 2 3 +1 2 x − 2 2 x − 2 2 x − . 2 x − 2 6
Dấu bằng xảy ra khi và chỉ khi =
x = 2 + 2 3 (vì x  2) 2 x − 2
Vậy giá trị nhỏ nhất của hàm số f (x) là 2 2
2 3 +1  a = 2; b = 1  a + b = 5.
Chú ý: Trong đề gốc thiếu giả thiết a, b là các số nguyên, chúng tôi đã phải thêm điều kiện này vào trong đề ra để
bài toán có thể giải được. (x − 2)(mx + ) 1
Câu 42. Số các giá trị thực của tham số m để phương trình = 0 x + có nghiệm duy nhất là 1 A. 3 . B. 2 . C. 0 . D.1. Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang Chọn A (x −2)(mx + ) 1 = 0 ( )1 x +1
Điều kiện xác định : x  1 − . x − = x = 2
Với điều kiện trên, phương trình ( )
1  ( x − )(mx + ) 2 0 2 1 = 0     mx +1 = 0 mx = −1  (2) Phương trình ( )
1 có nghiệm duy nhất  (2) vô nghiệm hoặc (2) có nghiệm x = 2 hoặc (2) có nghiệm x = 1 − . 1
(2) vô nghiệm khi m = 0 ; (2) có nghiệm x = 2 khi m = −
; (2) có nghiệm x = 1 − khi m =1 . 2
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 21
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020
Câu 43. Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x − 2x +1 = m có hai nghiệm phân biệt. A. m  0 . B. m  0 .
C. m 1 hoặc m = 0 .
D. 0  m 1. Lời giải
Tác giả:Đặng Thị Phương Huyền; Fb: Phuong Huyen Dang Chọn C 4 2
x − 2x +1 = m (1) Đặt 2
t = x ( t  0 ).
Khi đó phương trình (1) trở thành: 2
t − 2t +1 = m 2
t − 2t +1− m = 0 . (2)
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt trái dấu hoặc có nghiệm kép dương ac  0 1  − m  0      m 1  ' = 0   m = 0   .    =   m 0 S  0 2  0
Câu 44. Tìm tất cả các giá trị thực của tham số m để phương trình 3 2
x − mx − x + m = 0 có ba nghiệm thực phân biệt. A. m  1 − . B. m  1  .
C. m  1 hoặc m = 0 . D. 0  m  1 . Lời giải
Tác giả: ; Fb: Chọn Bx = 1  3 2 2
x − mx − x + m = 0  x(x −1) − m ( 2 x − ) 1 = 0  ( 2 x − )
1 ( x − m) = 0   .  x = m ycbt  m  1  .
Câu 45. Cho phương trình 2
−x + mx + m +1 = 0 với m là tham số thực. Tính tổng S tất cả các giá trị thực của tham
số m để phương trình có hai nghiệm phân biệt x , x thỏa mãn x + x = 4 . 1 2 1 2 A. S = 2 B. S = 2 − . C. S = 4 − D. S = 5. Lời giải
Tác giả: ; Fb: Chọn B
Phương trình có hai nghiệm phân biệt x ; x Û D > 0 1 2
Û m + (m + ) > Û (m + )2 2 4 1 0 2 > 0 Û m ¹ - 2.
Khi đó phương trình có hai nghiệm phân biệt: −m + (m + 2) −m − (m + 2) x = = 1 − , x = = m +1 1 2 2 − 2 − .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 22
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 m +1 = 3  m = 2
Ta có x + x = 4  1 + m + 1 = 4  m + 1 = 3    (t ) m . 1 2  m +1 = 3 −  m = 4 − Suy ra S = 2 − .
Câu 46: Cho phương trình 2
x −10x + m = 2 − x . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho vô nghiệm .
A.16  m  20 . B. 3 −  m 16 C. m . D. m  16 . Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh Chọn D. 2 − x  0  x  2 2
x −10x + m = 2 − x    
x −10x + m =  (2− x)2 2 2 2
x −10x + m = 4 − 4x + x    x 2 x  2      m − 4 6x = m − 4 x =  6 m − 4
Để phương trình vô nghiệm thì
 2  m − 4  12  m  16 . 6
Câu 47: Tập tất cả các giá trị của tham số m để phương trình 2 2
x + 1− x = m có tập nghiệm là  ;ab. Tính
S = a + b ? 9 1 A. 0. B. . C.1. D. . 4 4 Lời giải
Tác giả: Trịnh Xuân Mạnh ; Fb:Trịnh Xuân Mạnh. Chọn B 2 1  − x  0   1 −  x 1  2 2
x + 1− x = m     2 2
−(1− x ) + 1− x +1− m = 0 2 2  (
− 1− x ) + 1− x +1− m = 0 Đặt 2
1− x = t . Điều kiện t 0; 
1 . Phương trình (*) trở thành : 2 t
− + t +1= m (**)
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số 2 f (t) = t
− + t +1 trên 0;  1 và đường
thẳng y = m vuông góc với trục Oy .  1 5  Xét đồ 2
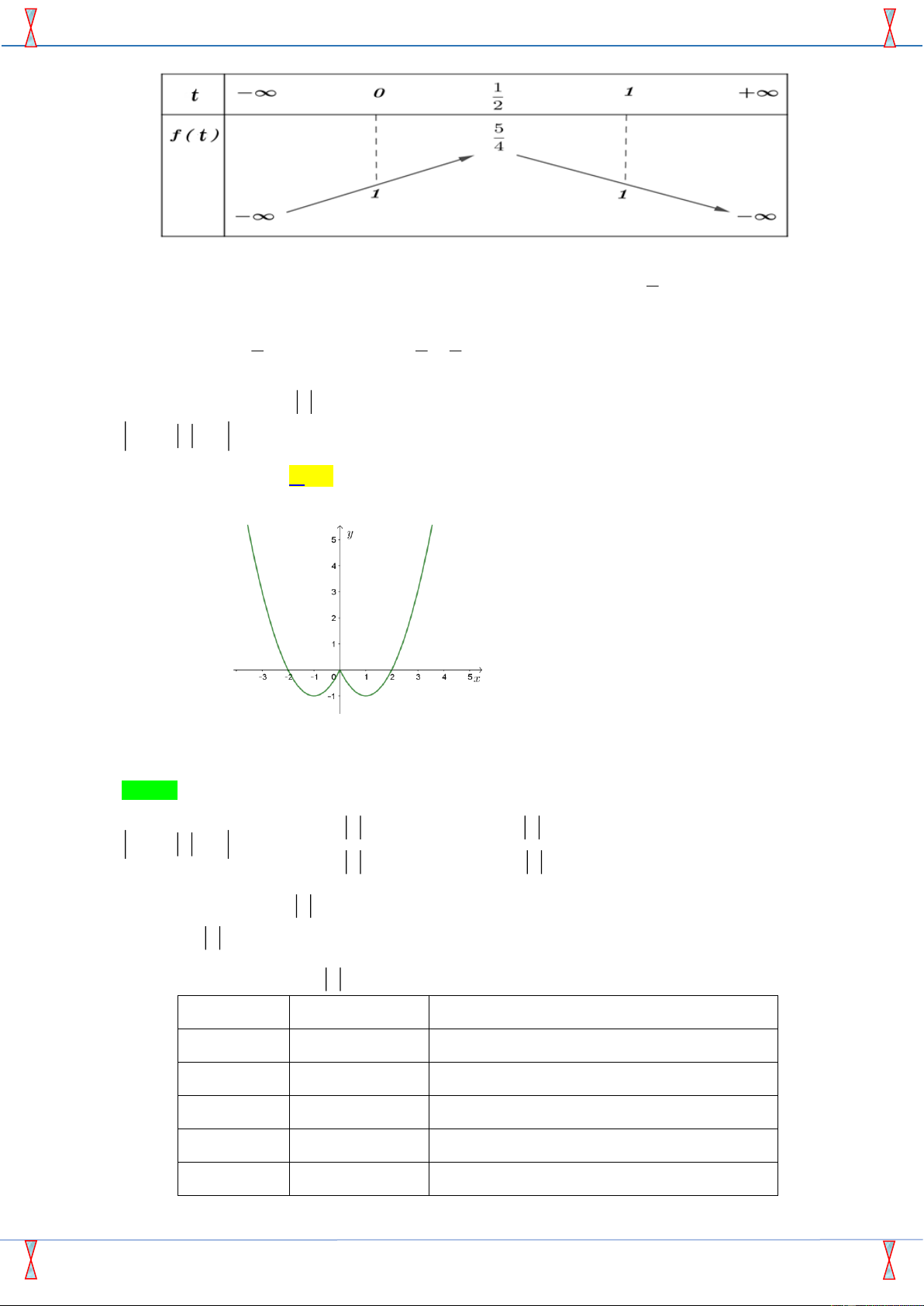
thị hàm số f (t) = t
− + t +1 là đường parabol có đỉnh là điểm I ;   , vì a = 1 −  0 nên bề  2 4 
lõm quay xuống dưới. Ta có bảng biến thiên sau :
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 23
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020  5
Dựa vào bảng biến thiên, ta có: Phương trình (**) có nghiệm  m  1;   .  4 5 5 9 Vậy a = 1;b =
S = a + b = 1 + = . 4 4 4 Câu 48: Cho hàm số 2
y = x − 2 x có đồ thị như hình vẽ. Gọi S là tập các giá trị nguyên của m đề phương trình 2
x − 2 x + m = 1 có hai nghiệm phân biệt. Tính tổng các phần tử của tập S . A. 1 − . B. 2 . C. 4 . D. 0 . Lời giải
Tác giả: Trần Thảo; Facebook: Trần Thảo Chọn B 2 2
x − 2 x + m = 1
x − 2 x = 1− m ( ) 1 2
x − 2 x + m = 1     2 2
x − 2 x + m = 1 −  x − 2 x = 1 − − m  (2) Xét phương trình 2
x − 2 x = k (3). Số nghiệm của phương trình này là số giao điểm của đồ thị hàm số 2
y = x − 2 x và đường thẳng y = k . Từ đồ thị hàm số 2
y = x − 2 x ta có kết luận sau: k Số giao điểm
Kết luận về số nghiệm của PT (3) k  1 − 0 Phương trình vô nghiệm k = 1 − 2
Phương trình có 2 nghiệm phân biệt 1 −  k  0 4
Phương trình có 4 nghiệm phân biệt k = 0 3
Phương trình có 3 nghiệm phân biệt k  0 2
Phương trình có 2 nghiệm phân biệt
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 24
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 Do 1
− − m 1− m ( m
  ) nên để phương trình đã cho có hai nghiệm phân biệt thì phương trình ( ) 1 có
hai nghiệm phân biệt và phương trình (2) vô nghiệm.  1 − − m  −1 m  0   m = 2
Điều đó tương đương với :  1
 − m = −1  m = 2   .   0  m  1 1  − m  0 m  1 Do m
nên m = 2 . Vậy S =  
2 . Tổng các phần tử của tập S là 2 .
Câu 49. Trong hệ tọa độ Oxy cho ba điểm A(1; 4
− ) , B(4;5) và C(0; 9
− ) . Điểm M di chuyển trên trục Ox . Đặt
Q = 2 MA + 2MB + 3 MB + MC . Biết giá trị nhỏ nhất của Q có dạng a b trong đó a , b là các số nguyên
dương và a , b  20. Tính a − b. A. 15 − . B. 17 − . C. 14 − . D. −11. Lời giải
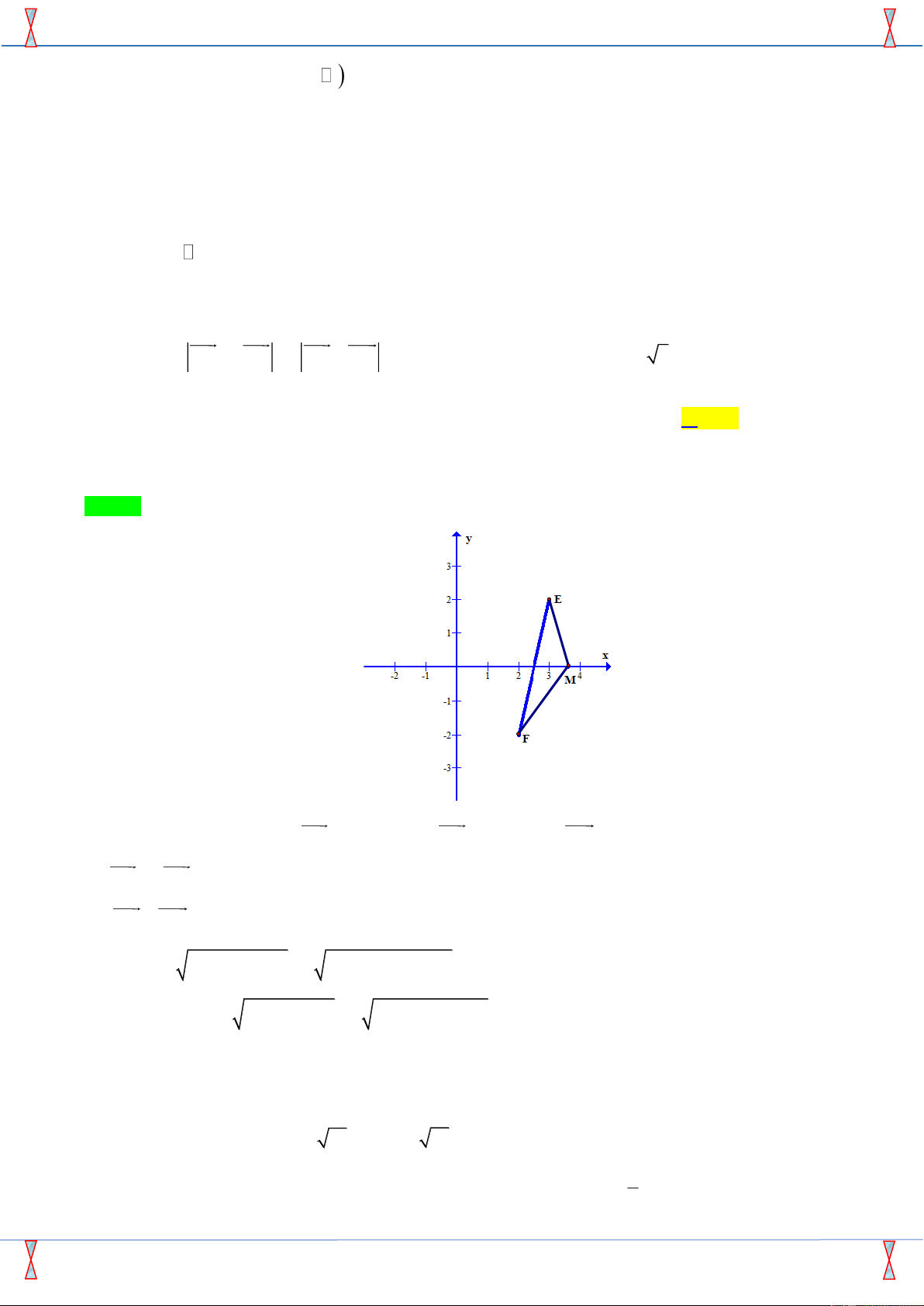
Tác giả: Nguyễn Thị Thanh Mai; Fb: Thanh Mai Nguyen Chọn D
Giả sử M ( x;0)Ox . Ta có: MA = (1− x; − 4) , MB = (4 − x;5) , MC = (−x; 9 − ) .
MA+ 2MB = (9 −3x;6) ,
MB + MC = (4 − 2x; 4 − ). Do đó Q =
( − x)2 + + ( − x)2 +(− )2 2 2 9 3 6 3 4 2 4 =
( − x)2 + + ( − x)2 2 2 6 3 2 6 2 + ( 2 − ) = 6(ME + MF).
Trong đó E (3;2) , F (2;− 2) .
Ta có ME + MF EF = 17  Q  6 17 5
Dấu “ = “ xảy ra  M là giao điểm của đoạn EF và trục Ox M ( ;0) . 2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 25
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề HK I lớp 10 Môn Toán THPT Lương Thế Vinh HN-2019-2020 a = 6
Suy ra Q đạt giá trị nhỏ nhất là 6 17 . Do đó theo giả thiết ta có 
.Vậy a − b = 11 − . b  =17
Câu 50. Cho x, y thoả mãn 2 2
x + y = a . Xác định a , biết rằng giá trị lớn nhất của P = 2x + 3y với x, y  0 là 117 . A. a = 9 . B. a = 13 . C. a = 5 .
D. a = 3 3 . Lời giải
Tác giả: Vũ Thị Thu Huyền; Fb: HuyenVu Chọn A. Ta có : 2 2
a = x + y  0
P = ( x + y)2 2  ( 2 2 + )( 2 2 x + y ) 2 2 3 2 3  P 13a .  2 ax yx =  =  13
P = 13a   2 3  
(do x  0, y  0)  2 2  3 a
x + y = a y =  13
Vậy MaxP = 13a . Theo giả thiết, ta có: 13a = 117  a = 9 .
---------- HẾT ----------
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 26