Đề thi HK1 Toán 10 năm 2019 – 2020 trường THPT Lương Thế Vinh – TP HCM

Nhằm giúp các em học sinh lớp 10 có tư liệu ôn tập để chuẩn bị cho kỳ thi học kì 1 môn Toán 10, xin giới thiệu đến các em nội dung đề thi HK1 Toán 10 năm học 2019 – 2020 trường THPT Lương Thế Vinh, thành phố Hồ Chí Minh, mời bạn đọc đón xem

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
Trường THPT Lương Thế Vinh
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
Môn: TOÁN 10 – Thời gian: 90 phút
Câu 1 (2 điểm): Khảo sát sự biến thiên và vẽ đồ thị hàm số
2
2 1
y x x
.
Câu 2 (1 điểm): Định tham số
m
để phương trình
2
2 2 3 1 0
m x m x m
có hai
nghiệm phân biệt
1 2
,
x x
thỏa mãn
2 2
1 2 1 2
3 1
x x x x
.
Câu 3 (3 điểm): Giải các phương trình và hệ phương trình sau
a)
2 2
2 4 5 3 3 6
x x x x
b)
2
2
3 2
3 2
x x y
y y x
Câu 4 (1 điểm): Trong hệ trục tọa độ
Oxy
, cho tam giác
ABC
với
1; 2 ; 1;2 ; 4; 1
A B C
. Xác định tọa độ trực tâm
H
của tam giác
ABC
.
Câu 5 (2 điểm): Cho tam giác
ABC
có
5; 8
AB AC
, góc
60
A
.
a) Tính độ dài cạnh
BC
, trung tuyến
AM
.
b) Trên cạnh
BC
lấy điểm
N
sao cho
3
BN
, tính độ dài đoạn thẳng
AN
.
Câu 6 (1 điểm): Một người ném một quả bóng với quỹ
đạo là một phần đường Parabol
P
:
2
0
y ax bx c a
. Chọn hệ trục tọa độ
Oxy
sao cho
gốc tọa độ
O
tại vị trí chân người ném bóng, trục Ox
nằm trên mặt đất (
,
x y
được tính bằng mét) (xem hình
bên). Quả bóng được ném lên từ độ cao
2,5
mét so với
mặt đất, Parabol có đỉnh
9
2;
2
I
. Hỏi vị trí bóng chạm
mặt đất cách chân người đó bao nhiêu mét?
- HẾT -
Lưu ý: Học sinh ghi “ĐỀ LẺ” vào bài làm của mình.
Đ
Ề
L
Ẻ
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
Trường THPT Lương Thế Vinh
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
Môn: TOÁN 10 – Thời gian: 90 phút
Câu 1 (2 điểm): Khảo sát sự biến thiên và vẽ đồ thị hàm số
2
2 1
y x x
.
Câu 2 (1 điểm): Định tham số
m
để phương trình
2
3 2 5 2 0
m x m x m
có hai
nghiệm phân biệt
1 2
,
x x
thỏa mãn
2 2
1 2 1 2
3 1
x x x x
.
Câu 3 (3 điểm): Giải các phương trình và hệ phương trình sau
a)
2 2
2 4 2 7 3 6
x x x x
b)
2
2
3 2
3 2
x x y
y y x
Câu 4 (1 điểm): Trong hệ trục tọa độ
Oxy
, cho tam giác
ABC
với
1; 1 ; 1;3 ; 4;0
A B C
. Xác định tọa độ trực tâm
H
của tam giác
ABC
.
Câu 5 (2 điểm): Cho tam giác
ABC
có
8; 5
AB AC
, góc
60
A
.
a) Tính độ dài cạnh
BC
, trung tuyến
AM
b) Trên cạnh
BC
lấy điểm
N
sao cho
4
CN
, tính độ dài đoạn thẳng
AN
.
Câu 6 (1 điểm): Một người ném một quả bóng với quỹ
đạo là một phần đường Parabol
P
:
2
0
y ax bx c a
. Chọn hệ trục tọa độ
Oxy
sao cho
gốc tọa độ
O
tại vị trí chân người ném bóng, trục Ox nằm
trên mặt đất (
,
x y
được tính bằng mét) (xem hình bên).
Quả bóng được ném lên từ độ cao
2,5
mét so với mặt đất,
Parabol có đỉnh
9
2;
2
I
. Hỏi vị trí bóng chạm mặt đất
cách chân người ném bóng bao nhiêu mét?
- HẾT -
Lưu ý: Học sinh ghi “ĐỀ CHẴN” vào bài làm của mình.
Đ
Ề
CH
Ẵ
N
ĐÁP ÁN VÀ THANG ĐIỂM TOÁN 10 – HKI/1920
Câu
Đ
ề
l
ẻ
Đi
ể
m
Đ
ề
ch
ẵ
n
1 TXĐ: D=R
Sự biến thiên
Đồng biến:
1;

, nghịch biến
;1

Đồ thị:
Đỉnh
1; 2
I
, trục đx: x=1
Bảng giá trị
1;2 ; 0; 1 ; 1; 2 ; 2; 1 ; 3;2
TXĐ: D=R
Sự biến thiên
Đồng biến:
1;

, nghịch biến
; 1

Đồ thị:
Đỉnh
1; 2
I
, trục đx: x=-1
Bảng giá trị
3;2 ; 2; 1 ; 1; 2 ; 0; 1 ; 1;2
2
12 1
m
Pt có hai nghiệm pb khi
0
0
1
0
12
m
a
m
Theo Viete
1 2
1 2
2 1
2
m
S x x
m
m
P x x
m
Ta có
2
2 2
1 2 1 2
3 2 1 5 2
x x x x m m m
2
14 1 0
m m
7 5 2 7 5 2
m m (nhận cả
2)
12 1
m
Pt có hai nghiệm pb khi
0
0
1
0
12
m
a
m
Theo Viete
1 2
1 2
2 1
2
m
S x x
m
m
P x x
m
Ta có
2
2 2
1 2 1 2
3 2 1 5 2
x x x x m m m
2
14 1 0
m m
7 5 2 7 5 2
m m (nhận cả 2)
3
a)
2 2
2 4 5 3 3 6
x x x x
Đặt
2
2
t x x
, pt trở thành
2
2 5 3 3
3 3 0
2 5 3 3
t t
t
t t
1
2( )
2
( )
9
t
t n
t l
Ta có
2
2 2 1 3 1 3
x x x x
2 2
2 4 5 7 3 6
x x x x
Đặt
2
2
t x x
, pt trở thành
2
2 2 3 7
3 7 0
2 2 3 7
t t
t
t t
7
3
3( )
17
( )
9
t
t n
t l
Ta có
2
2 3 1 3
x x x x
3 b)
2
2
3 2 1
3 2 2
x x y
y y x
Lấy (1) trừ (2) theo vế
1 0
x y x y
2
2
4 3 1
4 3 2
x x y
y y x
Lấy (1) trừ (2) theo vế
1 0
x y x y
TH1:
x y
, thay vào (1)
2
0
5 0
5
x
x x
x
0 0
5 5
x y
x y
TH2:
1
y x
, thay vào (1)
2
2 0 1 2
x x x x
1 2
2 1
x y
x y
Kết luận: hệ pt có 4 nghiệm
0;0 ; 5;5 ; 1;2 ; 2; 1
TH1:
x y
, thay vào (1)
2
0
7 0
7
x
x x
x
0 0
7 7
x y
x y
TH2:
1
y x
, thay vào (1)
2
1 13 1 13
3 0
2 2
x x x x
1 13 1 13
2 2
1 13 1 13
2 2
x y
x y
Kết luận: hệ pt có 4 nghiệm
1 13 1 13 1 13 1 13
0;0 ; 7;7 ; ; ; ;
2 2 2 2
4
Gọi
,
H x y
1, 2 , 1, 2
3, 3 ; 5,1
AH x y BH x y
BC AC
Ta có
4
0 3 3 3
3
5 7 1
0
3
x
AH BC x y
x y
BH AC
y
Vậy
4 1
;
3 3
H
Gọi
,
H x y
1, 1 , 1, 3
3, 3 ; 5,1
AH x y BH x y
BC AC
Ta có
4
0 3 3 0
3
5 8 4
0
3
x
AH BC x y
x y
BH AC
y
Vậy
4 4
;
3 3
H
5a)
b)
2 2 2
2 cos 49
7
BC AB AC AB AC A
BC
2 2 2
2
2 2 129
4 4
129
2
AB AC BC
AM
AM
2 2 2
1
cos
2 7
AB BC AC
B
AB BC
2 2 2
208
2 cos
7
4 91
7
AN AB BN AB BN B
AN
2 2 2
2 cos 49
7
BC AB AC AB AC A
BC
2 2 2
2
2 2 129
4 4
129
2
AB AC BC
AM
AM
2 2 2
1
cosC
2 7
AC BC AB
AC BC
2 2 2
247
2 cosC
7
247
7
AN AC CN AC CN
AN
6 Từ đề bài ta có các pt
2,5
c
4 2 4.5
a b c
4 0
a b
Từ đề bài ta có các pt
2,5
c
4 2 4.5
a b c
4 0
a b
Giải hệ phương trình ta được
1
; 2; 2,5
2
a b c
Suy ra pt
2
1
: 2 2,5
2
P y x x
Cho
2
1
2 2,5 0
2
x x
giải được
1(1) 5( )
x x n
Vậy khi bóng chạm đất thì cách chân
ngư
ờ
i đó 5m
Giải hệ phương trình ta được
1
; 2; 2,5
2
a b c
Suy ra pt
2
1
: 2 2,5
2
P y x x
Cho
2
1
2 2,5 0
2
x x
giải được
1(1) 5( )
x x n
Vậy khi bóng chạm đất thì cách chân người đó
5m
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
Trường THPT Lương Thế Vinh
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
Môn: TOÁN 10 – Thời gian: 90 phút ĐỀ LẺ
Câu 1 (2 điểm): Khảo sát sự biến thiên và vẽ đồ thị hàm số 2 y  x  2x 1.
Câu 2 (1 điểm): Định tham số m để phương trình m   2
2 x  2m 3 x  m 1  0 có hai
nghiệm phân biệt x , x thỏa mãn 2 2 x  x  3x x 1. 1 2 1 2 1 2
Câu 3 (3 điểm): Giải các phương trình và hệ phương trình sau 2 x  3x  2y a) 2 2
2x  4x  5  3  3x  6x b)  2 y  3y  2x
Câu 4 (1 điểm): Trong hệ trục tọa độ Oxy , cho tam giác ABC với A 1  ; 2
 ; B1;2;C 4; 
1 . Xác định tọa độ trực tâm H của tam giác ABC .
Câu 5 (2 điểm): Cho tam giác ABC có AB  5; AC  8 , góc A  60 .
a) Tính độ dài cạnh BC , trung tuyến AM .
b) Trên cạnh BC lấy điểm N sao cho BN  3, tính độ dài đoạn thẳng AN .
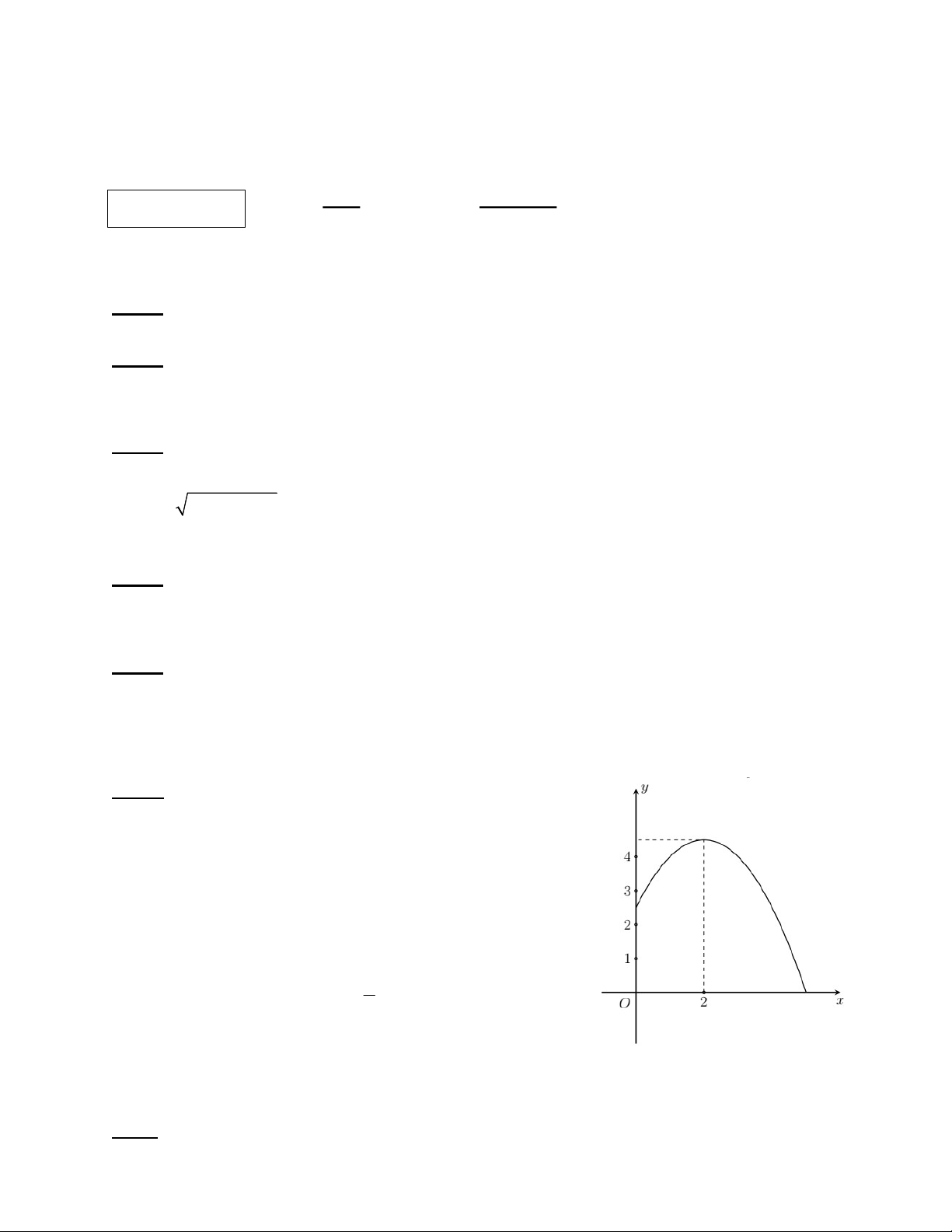
Câu 6 (1 điểm): Một người ném một quả bóng với quỹ đạo là một phần đường Parabol P: 2
y  ax  bx  c a  0 . Chọn hệ trục tọa độ Oxy sao cho
gốc tọa độ O tại vị trí chân người ném bóng, trục Ox
nằm trên mặt đất ( x, y được tính bằng mét) (xem hình
bên). Quả bóng được ném lên từ độ cao 2,5 mét so với  9 
mặt đất, Parabol có đỉnh I 2; 
 . Hỏi vị trí bóng chạm  2 
mặt đất cách chân người đó bao nhiêu mét? - HẾT -
Lưu ý: Học sinh ghi “ĐỀ LẺ” vào bài làm của mình.
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
Trường THPT Lương Thế Vinh
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
Môn: TOÁN 10 – Thời gian: 90 phút ĐỀ CHẴN
Câu 1 (2 điểm): Khảo sát sự biến thiên và vẽ đồ thị hàm số 2 y  x  2x 1.
Câu 2 (1 điểm): Định tham số m để phương trình m   2
3 x  2m  5 x  m  2  0 có hai
nghiệm phân biệt x , x thỏa mãn 2 2 x  x  3x x 1. 1 2 1 2 1 2
Câu 3 (3 điểm): Giải các phương trình và hệ phương trình sau 2 x  3x  2y a) 2 2
2x  4x  2  7  3x  6x b)  2 y  3y  2x
Câu 4 (1 điểm): Trong hệ trục tọa độ Oxy , cho tam giác ABC với A 1  ; 
1 ; B 1;3;C 4;0 . Xác định tọa độ trực tâm H của tam giác ABC .
Câu 5 (2 điểm): Cho tam giác ABC có AB  8; AC  5 , góc A  60 .
a) Tính độ dài cạnh BC , trung tuyến AM
b) Trên cạnh BC lấy điểm N sao cho CN  4 , tính độ dài đoạn thẳng AN .
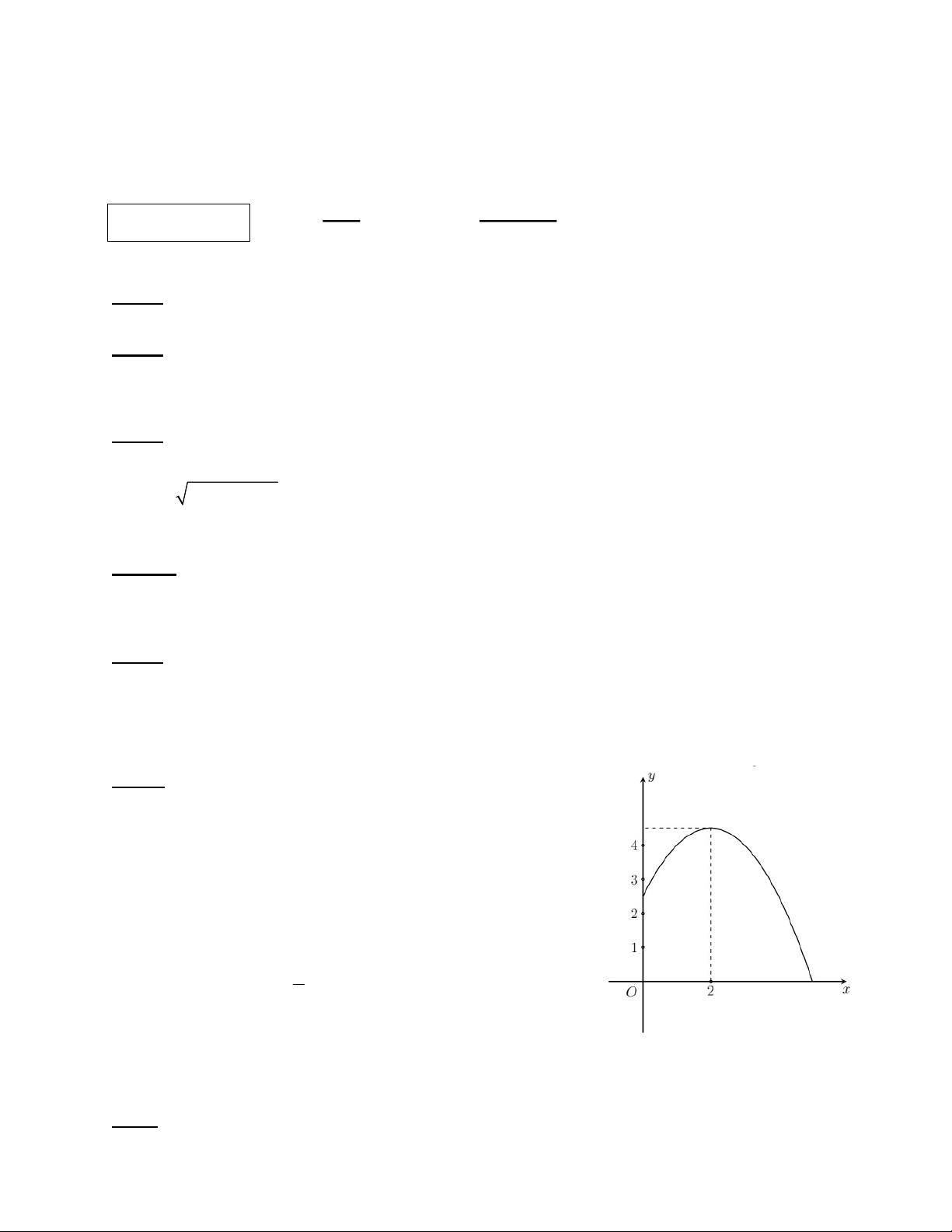
Câu 6 (1 điểm): Một người ném một quả bóng với quỹ đạo là một phần đường Parabol P: 2
y  ax  bx  c a  0 . Chọn hệ trục tọa độ Oxy sao cho
gốc tọa độ O tại vị trí chân người ném bóng, trục Ox nằm
trên mặt đất ( x, y được tính bằng mét) (xem hình bên).
Quả bóng được ném lên từ độ cao 2,5 mét so với mặt đất,  9  Parabol có đỉnh I 2; 
 . Hỏi vị trí bóng chạm mặt đất  2 
cách chân người ném bóng bao nhiêu mét? - HẾT -
Lưu ý: Học sinh ghi “ĐỀ CHẴN” vào bài làm của mình.
ĐÁP ÁN VÀ THANG ĐIỂM TOÁN 10 – HKI/1920 Câu Đề lẻ Điểm Đề chẵn 1 TXĐ: D=R TXĐ: D=R Sự biến thiên Sự biến thiên
Đồng biến: 1; , nghịch biến  ;   1 Đồng biến:  1
 ; , nghịch biến  ;    1 Đồ thị: Đồ thị: Đỉnh I 1; 2   , trục đx: x=1 Đỉnh I  1  ; 2   , trục đx: x=-1 Bảng giá trị Bảng giá trị  1  ;2;0;  1 ;1; 2  ;2;  1 ;3;2  3  ;2; 2  ;  1 ; 1  ; 2  ;0;  1 ;1;2 2   1  2m 1  12m 1 Pt có hai nghiệm pb khi Pt có hai nghiệm pb khi m  0    m 0 a  0  a  0     1    1    0 m     0 m   12  12 Theo Viete Theo Viete  2m 1  2m 1 S  x  x   S  x  x  1 2  m  1 2  m   m  2  m  2 P  x x  P  x x  1 2  m 1 2  m Ta có
Ta có x  x  3x x  2m  2 2 2 1  5m m  2 1 2 1 2  
x  x  3x x  2m  2 2 2 1  5m m  2 1 2 1 2   2  m 14m 1  0 2  m 14m 1  0
 m  7  5 2  m  7  5 2 (nhận cả 2)
 m  7  5 2  m  7  5 2 (nhận cả 2) 3 2 2
2x  4x  5  3  3x  6x 2 2
2x  4x  5  7  3x  6x a) Đặt 2
t  x  2x , pt trở thành Đặt 2
t  x  2x , pt trở thành 2t  5  3t  3 t  1  7  2t  2  3t  7 t   3 3  t  3  0 t  2(n)            2 3t 7 0   t  3(n) 2t  5    3t 32 t  (l)      9 2t  2   3t 72 17 t  (l) Ta có  9 2
x  2x  2  x  1 3  x  1 3 Ta có 2
x  2x  3  x  1 x  3 3 b) 2 x  3x  2y   1 2 x  4x  3y   1   2  y  3y  2x  2 2  y  4y  3x  2 Lấy (1) trừ (2) theo vế Lấy (1) trừ (2) theo vế
x  yx  y  1  0
x  yx  y  1  0 TH1: x  y , thay vào (1) TH1: x  y , thay vào (1) x  0 x  0 2 x  5x  0   2 x  7x  0   x  5 x  7 x  0  y  0 x  0  y  0 x  5  y  5 x  7  y  7
TH2: y  1 x , thay vào (1)
TH2: y  1 x , thay vào (1) 2
x  x  2  0  x  1 x  2 1 13 1 13 2 x  1 y  2 x  x  3  0  x   x  2 2 x  2  y  1 1 13 1 13
Kết luận: hệ pt có 4 nghiệm x   y  2 2  0;0;5;5; 1  ;2;2;  1 1 13 1 13    x y 2 2
Kết luận: hệ pt có 4 nghiệm
    1 13 1 13  1 13 1 13  0;0 ; 7;7 ; ; ; ;   2 2   2 2      4 Gọi H  x, y Gọi H  x, y    
AH   x 1, y  2, BH   x 1, y  2 AH   x 1, y  
1 , BH   x 1, y  3    
BC  3, 3; AC  5,  1
BC  3,3; AC  5,  1 Ta có Ta có  4    4 x     x  AH  BC  0 3  x  3y  3  3 AH  BC  0 3  x  3y  0  3             BH  AC  0 5  x  y  7 1  BH  AC  0 5  x  y  8 4 y     y  3  3 Vậy  4 1    H ;   Vậy 4 4 H ;    3 3   3 3  5a) 2 2 2
BC  AB  AC  2AB  AC  cos A  49 2 2 2
BC  AB  AC  2AB  AC  cos A  49  BC  7  BC  7 2 2 2 2AB  2AC  BC 129 2 2 2 2AB  2AC  BC 129 2 AM   2 AM   4 4 4 4 129  129 AM   AM  2 2 2 2 2 AB  BC  AC 1 2 2 2 AC  BC  AB 1 cos B   cosC   2AB  BC 7 2AC  BC 7 b) 208 2 2 2 247
AN  AB  BN  2AB  BN  cos B  2 2 2
AN  AC  CN  2AC CN cosC  7 7 4 91  247 AN   AN  7 7 6
Từ đề bài ta có các pt
Từ đề bài ta có các pt c  2,5 c  2,5 4a  2b  c  4.5 4a  2b  c  4.5 4a  b  0 4a  b  0
Giải hệ phương trình ta được
Giải hệ phương trình ta được 1  1  a  ;b  2;c  2,5 a  ;b  2;c  2,5 2 2   Suy ra pt  1 P 1 2 : y  x  2x  2,5 Suy ra pt P 2 : y  x  2x  2,5 2 2   Cho 1 1 2
x  2x  2,5  0 giải được Cho 2
x  2x  2,5  0 giải được 2 2 x  1(1)  x  5(n) x  1(1)  x  5(n)
Vậy khi bóng chạm đất thì cách chân
Vậy khi bóng chạm đất thì cách chân người đó người đó 5m 5m