


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019-2020 THÀNH PHỐ HỒ CHÍ MINH
Môn: Toán - KHỐI: 10
TRƯỜNG THPT TÂN PHONG
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Họ và tên HS: .................................................................................... SBD .................................... ……….
Câu 1: (1,0 điểm) Cho A = (−∞;−2];B = (−3;−2) ; tìm A∩ ; B A ∪ ; B A \ ; B C A .
Câu 2: (1,0 điểm) Tìm tập xác định của hàm số
3 + x − 3 − x y = . x ( 2 4x + x − 5) Câu 3: (2,0 điểm)
a) Khảo sát và vẽ đồ thị hàm số 2
y 2x 2 . b) Cho P 2
: y ax bx ca 0, tìm a,b,c biết (P) có hoành độ đỉnh là -2 và đi qua hai điểm A(2;− ) 1 ;B(−4;3) .
Câu 4: (3,0 điểm) Giải các phương trình sau: a) 2
x − 2x + 4 = 2 + x
b) 2 − 2 x + 5 = −x
c) 3x + 7 − x +1 = 2 Câu 5: (3,0 điểm)
a) Cho ∆ABC có trung tuyến CM. Trên đường thẳng AC lấy điểm N sao cho NA = 2NC . Gọi K là
trung điểm MN. Phân tích vecto AK theo AB, AC .
b) Trong mặt phẳng Oxy , cho tam giác ∆ABC có A(−1;2);B(3;7);C(0;3) . Tìm D sao cho ABCD là hình bình hành.
c) Trong mặt phẳng Oxy cho E(−2;−3);F(3;7);G(0;3);H (−4;−5) , chứng minh rằng hai đường thẳng
EF và GH song song với nhau. HẾT
HƯỚNG DẪN CHẤM TOÁN 10 CÂU ĐÁP ÁN ĐIỂM
Câu 1 cho A = (−∞;−2];B = (−3;−2). Tìm A∩ ; B A∪ ; B A \ ; B C A .
A∩ B = (−3;−2) (1,0 0,25
điểm) A∪ B = (−∞;−2] 0,25
A \ B = (−∞;− ] 3 ∪{− } 2 0,25 C A = (−2;+∞ 0,25 ) Câu 2 (1,0 3+ x − 3− x điểm) y = x ( 2 4x + x − 5) x ≥ −3 3 + x ≥ 0 x ≤ 3 0,5+0.25 3 − x ≥ 0 Hàm số xác định khi: ⇔ x ≠ 0 x ≠ 0 x ≠1 2
4x + x −5 ≠ 0 −5 x ≠ 4 0,25 Vậy D [ ] 5 3;3 \ ;0;1 = − − . 4 Câu 3
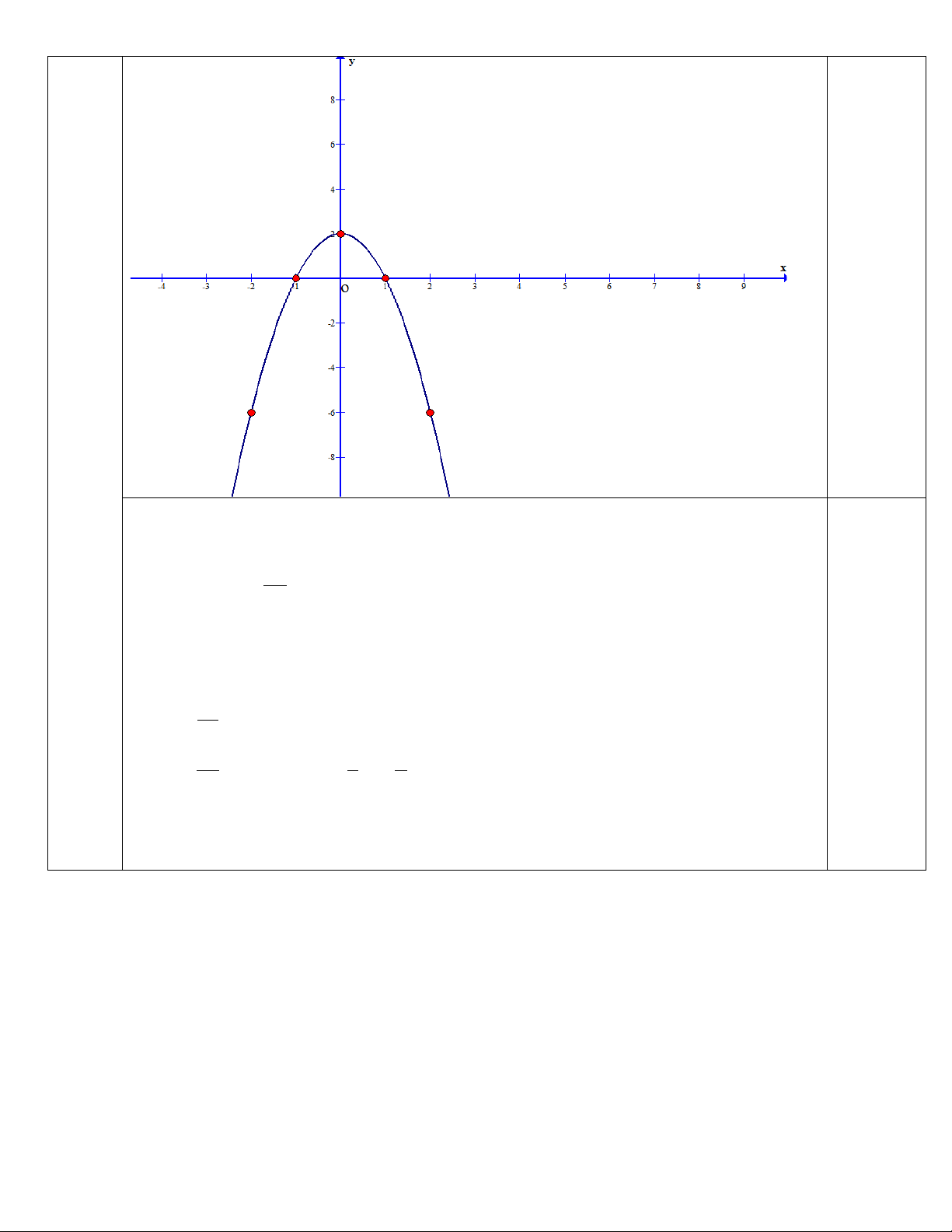
a) Khảo sát và vẽ đồ thị hàm số 2
y 2x 2 (2,0 D = điểm)
Tọa độ đỉnh: I (0;2)
Trục đối xứng x = 0 0,25
Bảng biến thiên: a = −2 < 0 x −∞ 0 +∞ y 2 0,25 −∞ −∞ Bảng giá trị: x -2 -1 0 1 2 y 0,25 -6 0 2 0 -6 0,25 b) Cho P 2
: y ax bx ca 0, tìm a,b,c biết (P) có hoành độ đỉnh là −2
và đi qua hai điểm A(2;− ) 1 ; B(−4;3) −b = −2 2a −4a + b = 0 Theo đề ta có: A(2;− )
1 ∈(P) ⇔ 4a + 2b + c = −1 0,25*3
B(−4;3)∈(P) 16
a − 4b + c = 3 −1 a = 3 −4 ⇔ 1 4 b = vậy (P) 2
: y = − x − x + 3 3 3 3 0,25 c = 3 Câu 4 a) 2
x − 2x + 4 = 2 + x (3,0 2 + x ≥ 0 điểm) ⇔ 0,25 2
x − 2x + 4 = 2 + x x ≥ −2 ⇔ 2
x − 3x + 2 = 0 0,25 x ≥ −2 ⇔
x = 1( Nhan) 0,25
x = 2( Nhan) Vậy 0,25 S = {1; } 2 . b)
2 − 2 x + 5 = −x
⇔ 2 x + 5 = 2 + x 0,25 2 + x ≥ 0 x ≥ −2 ⇔ ⇔ 0,25 4( x + 5) 2 = 4 + 4x + x 2 x −16 = 0 x ≥ −2 ⇔ 0,25+0.25
x = 4(nhan) vậy S = { } 4 .
x = −4(loai) c)
3x + 7 − x +1 = 2(*) 7 3x + 7 ≥ 0 x ≥ − 0,25 Điều kiện: ⇔ 3 ⇔ x ≥ −1 x +1 ≥ 0 x ≥ −1
(*) ⇔ 3x + 7 = 2+ x +1
⇔ 3x + 7 = 4 + 4 x +1 + x +1
⇔ 2x + 2 = 4 x +1 0,25 2x + 2 ≥ 0 ⇔ 2
4x + 8x + 4 = 16( x + ) 1 0,25 x ≥ −1 ⇔ 2
4x − 8x −12 = 0 x ≥ −1 ⇔ x = −1 x = 3
So với điều kiện, nhận cả hai nghiệm Vậy S = {−1; } 3 0,25 . Câu 5 (3,0
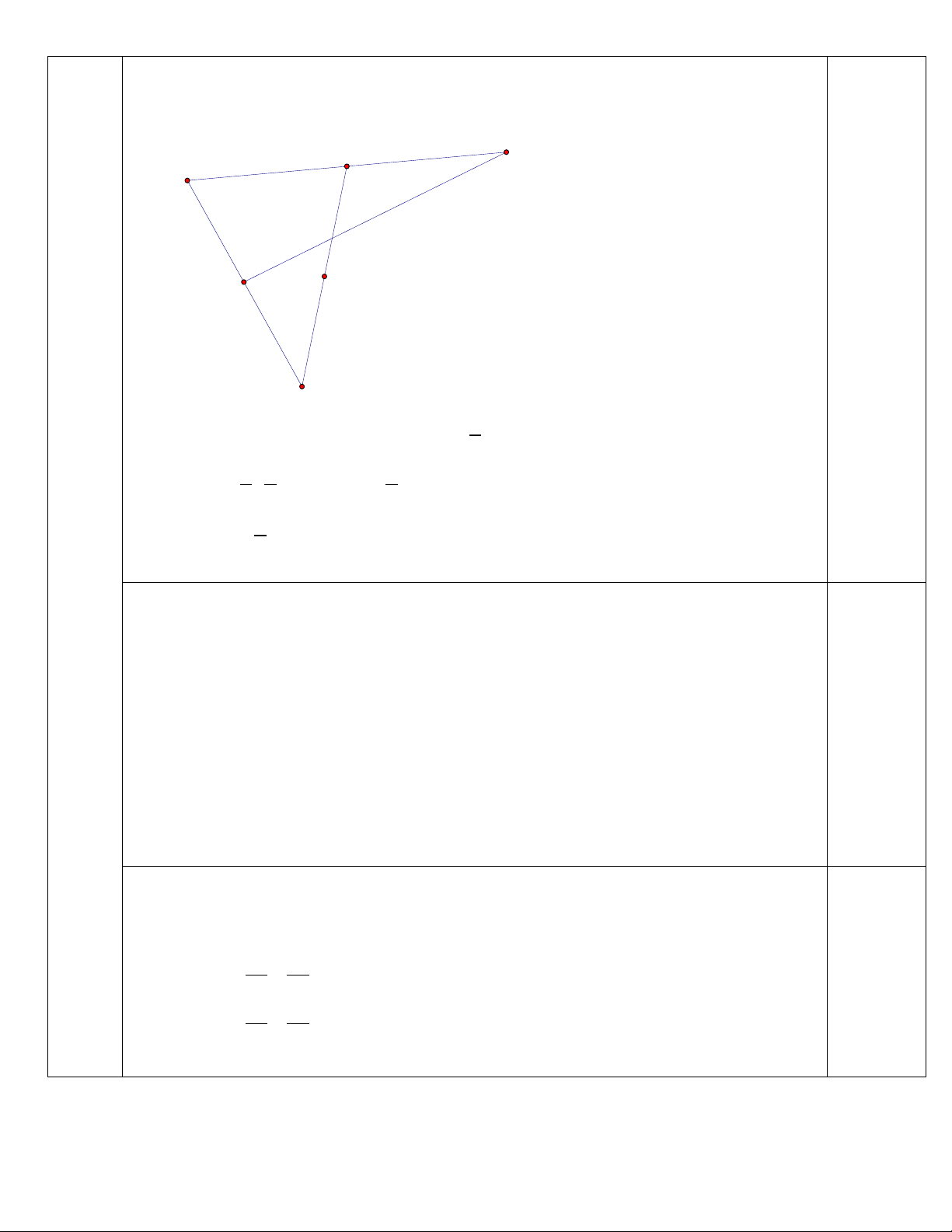
a) Cho ∆ABC có trung tuyến CM. Trên đường thẳng AC lấy điểm N sao cho điểm)
NA = 2NC . Gọi K là trung điểm MN. Phân tích vecto AK theo AB, AC . M B A K C N
K là trung điểm MN nên ta có: 1
AK = ( AM + AN ) 2 0,25
1 1
1 ⇔ AK =
AB + 2AC = AB + AC 2 0,25*3 2 4 Vậy 1
AK = AB + AC 4
b) Trong mặt phẳng Oxy, cho tam giác ∆ABC có A(−1;2);B(3;7);C(0;3).
Tìm D sao cho ABCD là hình bình hành.
Ta có: AB = (4;5);DC = (−x − D ; 3
yD )
ABCD là hình bình hành nên ta có AB = DC 0,25 −x = D 4 ⇒ 3− y = 0,25 D 5 x = − D 4 ⇔ 0,25 y = − D 2 Vậy D(−4;−2) . 0,25
c) Trong mặt phẳng Oxy , cho E (−2;−3);F(3;7);G(0;3);H (−4;−5) , chứng minh
rằng hai đường thẳng EF và GH song song với nhau.
Ta có: EF = (5;10);FG = (−3;−4);GH = (−4;−8) 0.25 5 10 • ≠
⇒ EF ≠ k FG k ∈ 1 ( 1 ) −3 −4 0,25 5 10 • =
⇒ EF = k GH k ∈ 0,25 2 ( 2 ) −4 −8 0.25 Vậy EF//GH.
Document Outline
- ĐỀ TOAN K10 - THPT TÂN PHONG Tp. Hồ Chí Minh
- ĐÁP ÁN TOAN 10 - THPT TÂN PHONG Tp. Hồ Chí Minh




