Đề thi HK1 Toán 10 năm 2019 – 2020 trường THPT Thủ Khoa Huân – TP HCM

Nhằm giúp các em học sinh lớp 10 có tư liệu ôn tập để chuẩn bị cho kỳ thi học kì 1 môn Toán 10, xin chia sẻ đến các em nội dung đề thi HK1 Toán 10 năm học 2019 – 2020 trường THPT Thủ Khoa Huân, thành phố Hồ Chí Minh, mời các bạn đón xem

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD – ĐT TP. HỒ CHÍ MINH
TRƯỜNG THPT THỦ KHOA HUÂN
ĐỀ THI HỌC KỲ I NĂM HỌC 2019 – 2020
Môn: Toán - lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian giao đề)
Đề thi gồm 01 trang
----------------------
Câu 1 (1.0đ) Tìm tập xác định của các hàm số sau đây:
a. (0.5đ )
2 1
.
3 2
x
y
x
b. (0.5đ)
2 5 .
y x x
Câu 2 (1.0đ) Xác định parabol
2
P y ax bx
biết
( )
P
đi qua điểm
(2;4)
A và
( )
P
nhận đường
thẳng
5
6
x
làm trục đối xứng.
Câu 3 (3.0đ) Giải các phương trình sau
a.(1đ)
2
2
1 4 3 3
3 3 9
x
x x x
b.(1đ)
2 5 4 0
x x
c.(1đ)
2
3 4 5 3 7
x x x
Câu 4 (1.0đ) Tìm
m
để phương trình
2
2(3 4) 1 0
x m x m
có hai nghiệm phân biệt
1 2
,
x x
sao
cho
1 2
1 2
1 1
3
x x
x x
.
Câu 5 (2.5đ) Trong mặt phẳng tọa độ
,
Oxy
cho
(1;3),B(2; 4), C(4;0).
A
a.(0.5đ) Chứng minh ba điểm
, ,
A B C
tạo thành một tam giác.
b.(0.75đ) Tìm tọa độ điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
c.(0.75đ) Tính độ dài đường trung tuyến
AM
của tam giác
.
ABC
d.(0.5đ) Tìm điểm
N
trên trục hoành sao cho tam giác
NAB
cân tại
N.
Câu 6 (1.0đ)
a. (0.5đ) Cho tam giác
ABC
có
6,
BC
ACB
= 45
, ABC
= 105
. Tính độ dài các cạnh
, .
AB AC
b.(0.5đ) Tính diện tích tam giác
MNP
trong hình vẽ sau (biết
G
là trọng tâm của tam giác).
Câu 7 (0.5đ) Bạn Nhi dùng
60
m lưới B40 rào thành một mảnh vườn hình chữ nhật để trồng hoa tết.
Biết rằng một cạnh của vườn là bờ sông nên Nhi chỉ cần rào 3 cạnh còn lại của mảnh vườn hình chữ
nhật. Theo em, bạn Nhi nên tính toán các kích thước của mảnh vườn như thế nào để diện tích trồng
hoa là lớn nhất? Tính diện tích lớn nhất đó.
- HẾT -
(Giám thị không giải thích gì thêm)
10
12
18
G
M
P
N
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM
CÂU Ý NỘI DUNG ĐIỂM
1
a
2 1
.
3 2
x
y
x
Hàm số xác định khi và chỉ khi
2
3 2 0 .
3
x x
0.25
Tập xác định
2
\ .
3
D
0.25
b
2 5 .
y x x
Hàm số xác định khi và chỉ khi
2 0 2
2 5.
5 0 5
x x
x
x x
0.25
Tập xác định
[2; 5].
D
0.25
2
( )
P
đi qua điểm
(2;4)
A nên ta có
2
4 .2 .2 2 4a 2 2 (1)
a b b
0.25
( )
P
nhận đường thẳng
5
6
x
làm trục đối xứng nên
5
5 3 0 (2)
2 6
b
a b
a
0.5
Từ (1) và (2) ta có hệ phương trình
4 2 2 3
.
5 3 0 5
a b a
a b b
Vậy
2
( ) : 3 5 2.
P y x x
0.25
3 a
Điều kiện:
2
3 0
3 0 3.
9 0
x
x x
x
0.25
Với điều kiện trên, PT
2
2
( 3) 4(x 3) 3 3
( 3)( 3) 9
x x
x x x
2
2 2
3 15 3 3
9 9
x x
x x
0.25
2
2
3 15 3 3
3 3 18 0
x x
x x
0.25
3 ( )
2 ( )
x
x
lo¹i
tháa®k
Vậy tập nghiệm của phương trình là
2 .
S
0.25
b
2
2 5 4 0
2 5 4
4 0
2 5 ( 4)
x x
x x
x
x x
0.25
2 2
4 4
2 5 8 16 10 21 0
x x
x x x x x
0.25
4
3
7
x
x
x
0.25
7.
x
0.25
Vậy tập nghiệm của phương trình là
7 .
S
c
2
2
2
2
3 4 5 3 7
3 4 5 3 7
3 7 0
3 4 5 3 7
3 4 5 3 7
x x x
x x x
x
x x x
x x x
0.25
2
2
7
3
3 7 2 0
3 12 0
x
x x
x x
0.25
7
3
1
1
3
2
3
2
1 145
1 145
6
6
1 145
1 145
6
6
x
x
x
x
x
x
x
x
x


Vậy tập nghiệm của phương trình là
1 1 145 1 145
; 2; ; .
3 6 6
S
0.5
4
Tìm
m
để phương trình
2
2(3 4) 1 0
x m x m
có hai nghiệm phân biệt
1 2
,
x x
sao cho
1 2
1 2
1 1
3
x x
x x
.
Giả sử phương trình
2
2(3 4) 1 0
x m x m
có hai nghiệm phân biệt
1 2
,
x x
.
Khi đó theo định lý Viet ta có
1 2
1 2
2(3m 4) 6m 8
1
x x
x x m
0.25
Ta có
1 2 1 2 1 2
1 2 1 2
1 1
3 3
6 8 6 8
1 3
1 1
(6m 8) 0
1 3
6 8 0
4
3
1 1
0
2
1 3
x x x x x x
x x x x
m m
m
m
m
m
m
m
0.5
Thử lại:
+ Khi
4
,
3
m
phương trình trở thành
2
7
0
3
x
(vô nghiệm).
+ Khi
2,
m
phương trình trờ thành
2
4 3.
x x
Do
' 1 0
nên phương
trình có hai nghi
ệ
m phân bi
ệ
t.
0.25
Vậy
2
m
là giá trị cần tìm.
5 a
Ta có
(1; 7)
AB

(3; 3)
AC

0.25
Vì
3 3
1 7
nên
AB

và
AC

không cùng phương. Do đó ba điểm
, ,
A B C
không
thẳng hàng. Hay
, ,
A B C
tạo thành tam giác.
0.25
b
Giả sử
(a;b)
D
Do
, ,
A B C
không thẳng hàng nên tứ giác
ABCD
là hình bình hành
DC AB
 
(*)
0.25
Mặt khác
(4 a; )
DC b

nên
4 1 3
(*)
7 7
a a
b b
Vậy
(3;7).
D
0.5
c
Trung điểm
M
của
BC
có tọa độ
2 4
3
2 2
4 0
2
2 2
B C
M
B C
M
x x
x
y y
y
Hay
(3; 2)
M
.
0.25
Độ dài trung tuyến
AM
2 2
2 2
( ) ( )
(3 1) ( 2 3) 29.
M A M A
AM x x y y
0.5
d
Gọi
N
là điểm thuộc
Ox
sao cho
.
AN BN
Giả sử
( ;0).
N a
Ta có
2 2
AN BN AN BN
0.25
2 2 2 2
(a 1) (0 3) (a 2) (0 4)
2 10 4 20
5.
a a
a
Khi đó
(5;0).
N
Ta kiểm tra được
, ,
A B N
là ba điểm không thẳng hàng nên chúng tạo thành
một tam giác. Vậy
(5;0)
N thì tam giác
NAB
cân tại
.
N
0.25
6 a
Ta có
𝐵𝐴𝐶
=
180
−
𝐴𝐵𝐶
−
𝐴𝐶𝐵
=
180
−
105
−
45
=
30
.
Áp dụng định lý sin trong tam giác
ABC
ta có
sin sin sinA
AB AC BC
C B
Suy ra
.sin 6.sin 45
6 2.
sin sin30
BC C
AB
A
0.25
.sinB 6.sin105
11.59
sin sin 30
BC
AC
A
0.25
b
Gọi
E
là trung điểm
.
NP
F
là điểm đối xứng với
G
qua
.
E
Khi đó tứ giác
NGPF
có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình
hành.
Ta có
3 3
MNP GNP GFP
S S S
(
GNP GFP
S S
vì cùng bằng nửa diện tích hình bình
hành).
Mặt khác
GPF
:
2 10,
GF GE GM
18
12
GP
PF NG
có nửa chu vi
20
p
nên
20(20 10)(20 18)(20 12) 40 2.
GPF
S
Vậy
3 3.40 2 120 2.
MNP GPF
S S
0.5
7
Gọi
x
(m) là kích thức đối diện bờ sông của mảnh vườn thì kích thước còn lại
của mảnh vườn là
60
30
2 2
x x
(m).
Diện tích của mảnh vườn:
2
1
30 30 .
2 2
x
y x x x
0.25
Vì
y
là hàm số bậc hai có
1
0
2
a
nên
y
lớn nhất khi
30
30.
1
2
2.
2
b
x
a
Khi đó các kích thước của mảnh vườn là
30
x
(m),
30 15
2
x
(m).
Và diện tích lớn nhất
max
(30) 450
y y
(
2
m
).
0.25
10
12
18
E
F
G
M
P
N
x
Bờ sông
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD – ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ I NĂM HỌC 2019 – 2020
TRƯỜNG THPT THỦ KHOA HUÂN Môn: Toán - lớp 10
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
(không kể thời gian giao đề) Đề thi gồm 01 trang ----------------------
Câu 1 (1.0đ) Tìm tập xác định của các hàm số sau đây: a. (0.5đ ) 2x 1 y  .
b. (0.5đ) y  x 2  5 x. 3x  2
Câu 2 (1.0đ) Xác định parabol 2
(P) : y  ax  bx  2 biết (P) đi qua điểm (
A 2;4) và (P) nhận đường thẳng 5
x  làm trục đối xứng. 6
Câu 3 (3.0đ) Giải các phương trình sau 2 a.(1đ) 1 4 3x 3  
b.(1đ) 2x 5  x  4  0 c.(1đ) 2 x 3 x  3 x 9 2
3x  4x  5 3x  7
Câu 4 (1.0đ) Tìm m để phương trình 2
x  2(3m  4)x  m 1 0 có hai nghiệm phân biệt x , x sao 1 2 cho 1 1 x  x 1 2   . x x 3 1 2
Câu 5 (2.5đ) Trong mặt phẳng tọa độ Oxy, cho ( A 1;3),B(2; 4  ), C(4;0).
a.(0.5đ) Chứng minh ba điểm ,
A B,C tạo thành một tam giác.
b.(0.75đ) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
c.(0.75đ) Tính độ dài đường trung tuyến AM của tam giác ABC.
d.(0.5đ) Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N . Câu 6 (1.0đ)
a. (0.5đ) Cho tam giác ABC có BC  6, ACB = 45 , ABC = 105 . Tính độ dài các cạnh AB, AC.
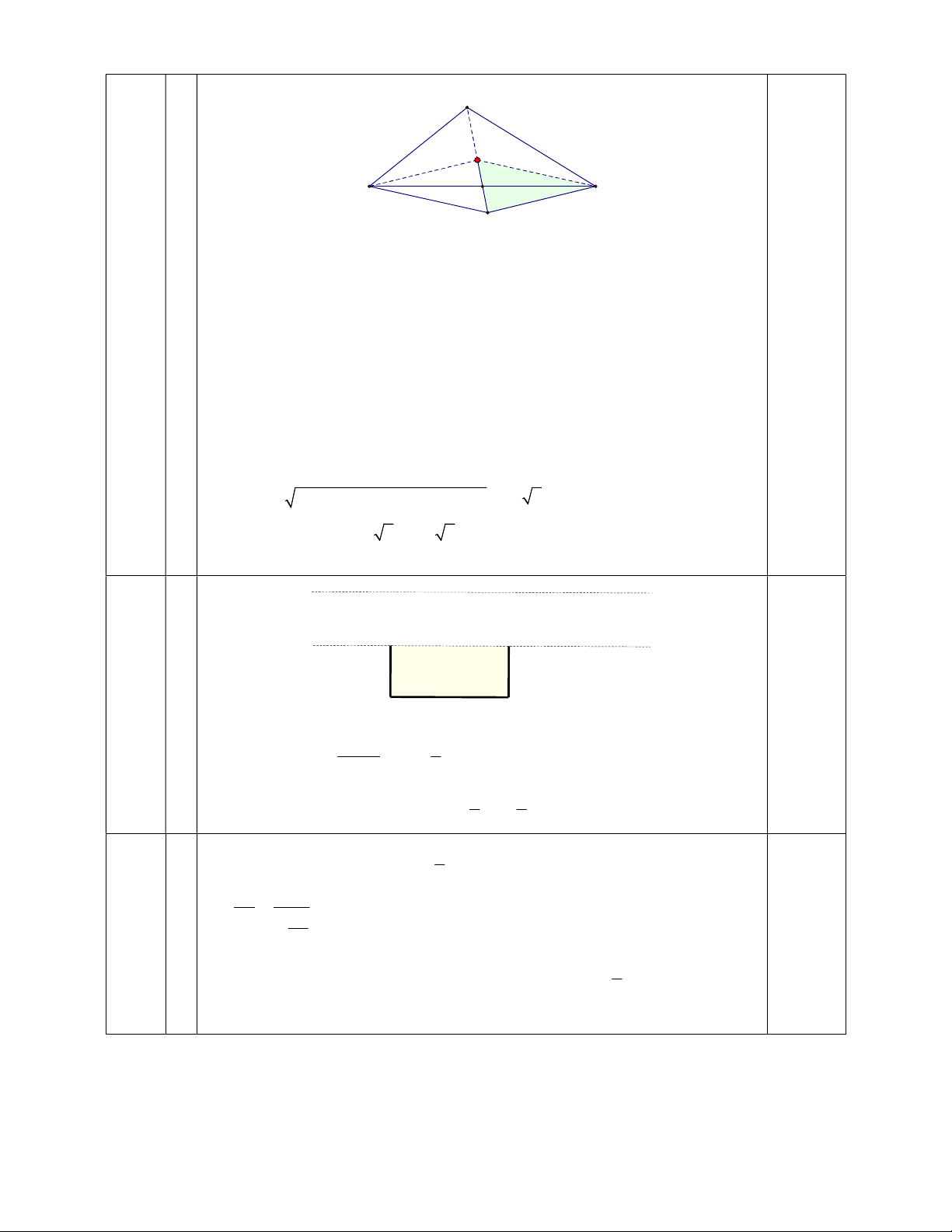
b.(0.5đ) Tính diện tích tam giác MNP trong hình vẽ sau (biết G là trọng tâm của tam giác). M 10 G 12 18 P N
Câu 7 (0.5đ) Bạn Nhi dùng 60 m lưới B40 rào thành một mảnh vườn hình chữ nhật để trồng hoa tết.
Biết rằng một cạnh của vườn là bờ sông nên Nhi chỉ cần rào 3 cạnh còn lại của mảnh vườn hình chữ
nhật. Theo em, bạn Nhi nên tính toán các kích thước của mảnh vườn như thế nào để diện tích trồng
hoa là lớn nhất? Tính diện tích lớn nhất đó. - HẾT -
(Giám thị không giải thích gì thêm) HƯỚNG DẪN CHẤM CÂU Ý NỘI DUNG ĐIỂM a 2x 1 y  . 3x  2 0.25
Hàm số xác định khi và chỉ khi 2 3x  2  0  x  . 3     0.25 1 Tập xác định 2 D  \    .    3   b y  x2  5 x. 0.25 x20   x  2
Hàm số xác định khi và chỉ khi      2  x 5. 5   x 0 x 5  
Tập xác định D [2; 5]. 0.25 (P) đi qua điểm ( A 2;4) nên ta có 2 4  . a 2  .
b 2  2  4a 2b  2 (1) 0.25 (P) nhận đường thẳng 5
x  làm trục đối xứng nên 6 b  5 2   5a 3b  0 (2) 2a 6 0.5 4a  2b  2   a  3
Từ (1) và (2) ta có hệ phương trình    .  5  a  3b  0 b    5  0.25 Vậy 2 (P) : y  3x 5x  2. 3 a x3 0   Điều kiện: x  3 0  x  3  . 0.25   2 x  9  0  2 (x  3) 4(x3) 3x 3
Với điều kiện trên, PT   2 (x 3)(x 3) x 9 2 3x 15 3x 3   0.25 2 2 x 9 x 9 2  3x 15  3x 3 2  3x 3x18  0 0.25 x  3  (lo¹ )i   x  2 (tháa®k)  0.25
Vậy tập nghiệm của phương trình là S  2. b 2x 5  x  4  0  2x 5  x  4 x4 0    2 2x  5  (x  4)  0.25 x  4 x  4   0.25     2 2 2  x
 5  x 8x 16 x   10x  21 0 x4    x  3 0.25  x7   x  7. 0.25
Vậy tập nghiệm của phương trình là S  7. c 2 3x  4x 5 3x  7 2
 3x  4x  5  3x  7 3  x  7  0   2 
 3x 4x 5  3x  7  0.25 2  3x  4x 5  3x 7  7  x    3     2  3x  7x  2  0  0.25 2 3x   x120  7  x    3  1   x   1  3  x    3 x 2     x 2   1   145   x    1   145  6 x     6  1    145  x   1 145      6 x    6        
Vậy tập nghiệm của phương trình là 1 1 145 1 145 S ; 2; ;      .  0.5  3 6 6    4
Tìm m để phương trình 2
x  2(3m  4)x  m 1 0 có hai nghiệm phân biệt 1 1 x  x x , x sao cho 1 2   . 1 2 x x 3 1 2 Giả sử phương trình 2
x  2(3m  4)x  m 1 0 có hai nghiệm phân biệt x , x . 1 2
Khi đó theo định lý Viet ta có
x  x  2(3m4)  6m8 1 2  0.25  x x  m 1 1 2  Ta có 1 1 x  x x  x x  x 1 2 1 2 1 2     x x 3 x x 3 1 2 1 2 6m 8 6m8   m 1 3  1 1  (6m8)   0  m 1 3 6m8 0  4   m    1 1   3    0  m  1 3 m  2  0.5 Thử lại: + Khi 4 7
m  , phương trình trở thành 2 x   0 (vô nghiệm). 3 3
+ Khi m  2, phương trình trờ thành 2
x 4x 3. Do ' 1 0 nên phương
trình có hai nghiệm phân biệt. 0.25
Vậy m  2 là giá trị cần tìm.  5 a Ta có AB(1;7)  0.25 AC(3;3)   Vì 3 3 
nên AB và AC không cùng phương. Do đó ba điểm , A B,C không 1 7 0.25 thẳng hàng. Hay , A B,C tạo thành tam giác. b Giả sử D(a;b) Do , A ,
B C không thẳng hàng nên tứ giác ABCD là hình bình hành    DC  AB (*) 0.25   4a 1   a  3 Mặt khác DC(4 a; b  ) nên (*)       b   7 b   7   Vậy D(3;7). 0.5 c Trung điểm M của BC có tọa độ  x  x 2  4 B C x     3 M  2 2   y  y 4  0 B C y   2 M  2 2 0.25 Hay M (3; 2  ) . Độ dài trung tuyến AM 2 2
AM  (x  x )  (y  y ) M A M A 0.5 2 2  (31) ( 2  3)  29. d Gọi
N là điểm thuộc Ox sao cho AN  BN. Giả sử N( ; a 0). 0.25 Ta có 2 2 AN  BN  AN  BN 2 2 2 2
(a1)  (03)  (a2) (0 4)  2  a 10 4a  20  a  5. Khi đó N(5;0). Ta kiểm tra được ,
A B, N là ba điểm không thẳng hàng nên chúng tạo thành
một tam giác. Vậy N(5;0) thì tam giác NAB cân tại N. 0.25 6 a
Ta có 𝐵𝐴𝐶 = 180 − 𝐴𝐵𝐶 − 𝐴𝐶𝐵 = 180 − 105 − 45 = 30 .
Áp dụng định lý sin trong tam giác ABC ta có AB AC BC   sin C sin B sinA Suy ra BC.sin C 6.sin 45 AB    6 2. 0.25 sin A sin 30 BC.sinB 6.sin105 AC   11.59 0.25 sin A sin 30 b M 10 G 12 18 N P E F Gọi E là trung điểm N .
P F là điểm đối xứng với G qua E. Khi đó tứ giác
NGPF có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành. Ta có S  3S  3S ( S
 S vì cùng bằng nửa diện tích hình bình MNP GNP GFP GNP GFP hành). Mặt khác G
 PF : GF  2GE  GM 10, GP 18 PF  NG 12 có nửa chu vi p  20 nên S
 20(2010)(2018)(2012)  40 2. GPF Vậy S  3S  3.40 2 120 2. 0.5 MNP GPF 7 Bờ sông x
Gọi x (m) là kích thức đối diện bờ sông của mảnh vườn thì kích thước còn lại
của mảnh vườn là 60 x x  30 (m). 2 2  x 1
Diện tích của mảnh vườn: 2 y  x 3  0
   x 30 .x   0.25 2 2
Vì y là hàm số bậc hai có 1
a    0 nên y lớn nhất khi 2 b  3  0 x    30. 2a 1  2. 2
Khi đó các kích thước của mảnh vườn là x
x  30 (m), 30 15 (m). 2 0.25
Và diện tích lớn nhất y  y(30)  450 ( 2 m ). max