Đề thi HK1 Toán 10 năm 2019 – 2020 trường THPT Thủ Thiêm – TP HCM

Nhằm giúp các em học sinh lớp 10 có tư liệu ôn tập để chuẩn bị cho kỳ thi học kì 1 môn Toán 10, xin giới thiệu đến các em nội dung đề thi HK1 Toán 10 năm học 2019 – 2020 trường THPT Thủ Thiêm, thành phố Hồ Chí Minh, mời bạn đọc đón xem

 

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Đề Toán khối 10 gồm có 1 trang Page 1/1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT THỦ THIÊM
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020
MÔN TOÁN – KHỐI 10
Thời gian làm bài 90 phút
(Không kể thời gian phát đề)
Câu 1
(1 điểm):
Khảo sát sự biến thiên và vẽ đồ thị hàm số
2
2 4 3
y x x
.
Câu 2 (1 điểm):
Tìm hàm số
2
8
y ax bx
biết đồ thị của hàm số là một parabol có đỉnh
S
Câu 3 (1 điểm):
Cho phương trình
2 2
2 5 16 0
x m x m với
m
là tham số. Tìm
m
để
phương trình có 2 nghiệm
1 2
,
x x
sao cho
2 2
1 1 2 2
2 5 2 10
x x x x
.
Câu 4 (1 điểm):
Giải phương trình
2
5 2 3 1
2 2
x x
x x x x
Câu 5 (1 điểm):
Giải phương trình
2
3 7 3 9
x x x
Câu 6 (1 điểm):
Giải phương trình:
2
x 3x 5 x 0
Câu 7 (1 điểm):
Giải phương trình:
2
2 2 12 2 3
x x x x
Câu 8 (3 điểm):
Trong
( )
mf Oxy
, cho ba điểm
(2; 1)
A
;
(4;4)
B
;
( 2; 4)
C
a) Chứng minh A, B, C tạo thành tam giác. Tính chu vi tam giác ABC.
b) Tìm D sao cho tứ giác AODC là hình bình hành. Tìm tọa độ tâm I của hình bình hành.
c) Tìm tọa độ trực tâm H của tam giác ABC.
-------------------------------------------------Hết-------------------------------------------------------
Học sinh không được sử dụng tài liệu. Cán bộ coi kiểm tra không được giải thích gì thêm.
Họ và tên học sinh: ………………………………………….Lớp: …………… SBD:………..…………
Đề Toán khối 10 gồm có 1 trang Page 2/1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT THỦ THIÊM
ĐỀ CHÍNH THỨC
ĐÁP ÁN KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020
MÔN TOÁN – KHỐI 10
Thời gian làm bài 90 phút
Câu 1
(1 điểm):
Khảo sát sự biến thiên và vẽ đồ thị hàm số
2
2 4 3 y x x
(1,0đ)
TXĐ D=R
Đỉnh
1; 5S
0.25đ
BBT x

1

y


-
5
Hàm số tăng trên
1;
và giảm trên
;1
0.25đ
ng giá tr
ị
x
-
1
0
1
2
3
y
3
-
3
-
5
-
3
3
0.25đ
Đồ thị
Parabol nhận đường thẳng
1x
làm trục đối xứng
0.25đ
Câu 2 (1 điểm): Tìm hàm số
2
8 y ax bx
biết đồ thị của hàm số là một parabol có
đỉnh
3;17S
Tìm hàm số
2
8 y ax bx
biết đồ thị của hàm số là một parabol có đỉnh
3;17S
(1,0đ)
3 6 0 (1)
2
b
a b
a
0.25đ
2
3 3 8 17 9 3 9 (2)
a b a b
0.25đ
(1)(2) suy ra
1
6
a
b
0.25đ
Vậy hàm số cần tìm là
2
6 8 y x x
0.25đ
Đề Toán khối 10 gồm có 1 trang Page 3/1
Câu 3 (1 điểm): Cho phương trình
2 2
2 5 16 0
x m x m với
m
là tham số. Tìm
m
để phương trình có 2 nghiệm
1 2
,
x x
sao cho
2 2
1 1 2 2
2 5 2 10
x x x x
.
Cho phương trình
2 2
2 5 16 0
x m x m , (
m
là tham số).
Tìm
m
để phương trình có 2 nghiệm
1 2
,
x x
sao cho
2 2
1 1 2 2
2 5 2 10
x x x x
.
(1,0đ)
20 89
m
0.25đ
Phương trình có 2 nghiệm
89
20
m
0.25đ
Định lý Viet:
2 5
S m
và
2
16
P m
2 2
1 1 2 2
2 5 2 10
x x x x
2
2 2 5 10
S P P
0.25đ
2
9 40 44 0
2
22
9
m m
m N
m N
0.25đ
Câu 4 (1 điểm): Giải phương trình
2
5 2 3 1
2 2
x x
x x x x
ĐK:
0
0, 25
2
x
x
PT
2
0
5 2 3 2 0, 25 7 0 0, 25 0, 25
7
x l
x x x x x x
x n
Câu 5 (1 điểm): Giải phương trình
2
3 7 3 9
x x x
2
2
2
2
33
3x-9 0
2
2 0
0,5 : 0,25
x +3x-7=3x-9
0,25
8
x +3x-7=-3x+9
6 16
xx
x l
x vn
TN S
x l
x x
Câu 6 (1 điểm): Giải phương trình:
2
x 3x 5 x 0
2
2
2
x 3x 5 x 0
x 3x 5 x
5 x 0
x 3x 5 x
x 5
x 1 N
x 5 N
Đề Toán khối 10 gồm có 1 trang Page 4/1
Câu 7 (1 điểm): Giải phương trình:
2
2 2 12 2 3
x x x x
2
2 2
2 2 12 2 3
2 12 6
x x x x
x x x x
Câu 8 (3 điểm): Trong
( )
mf Oxy
, cho ba điểm
(2; 1)
A
;
(4;4)
B
;
( 2; 4)
C
a) Chứng minh A, B, C tạo thành tam giác. Tính chu vi tam giác ABC.
b) Tìm D sao cho tứ giác AODC là hình bình hành. Tìm tọa độ tâm I của hình bình hành.
c) Tìm tọa độ trực tâm H của tam giác ABC.
a)
(2;5)
( 4; 3)
( 6; 8)
AB
AC
BC
29
5
10
AB
AC
BC
Thấy
2 5
,
4 3
AB AC
không cùng phương
, ,
A B C
tạo thành tam giác
Chu vi:
15 29
b)
(2; 1) ( 2 ; 4 )
2 2 4
4 1 1
( 4; 3)
D D
D D
D D
OA DC
x y
x x
y y
D
Tâm
I
của hình bình hành là trung điểm
OC
. Ta có:
( 1; 2)
I
c)
H
là trực tâm
ABC
. 0
. 0
106
3 4 2
7
4 3 28 76
7
106 76
( ; )
7 7
H
H H
H H
H
AH BC AH BC
BH AC
BH AC
x
x y
x y
y
H
-------------------------------------------------Hết-------------------------------------------------------
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020 THÀNH PHỐ HỒ CHÍ MINH MÔN TOÁN – KHỐI 10 TRƯỜNG THPT THỦ THIÊM
Thời gian làm bài 90 phút
(Không kể thời gian phát đề) ĐỀ CHÍNH THỨC Câu 1 (1 điểm):
Khảo sát sự biến thiên và vẽ đồ thị hàm số 2 y  2x  4x  3 . Câu 2 (1 điểm): Tìm hàm số 2
y  ax  bx  8 biết đồ thị của hàm số là một parabol có đỉnh S  3  ;17 Câu 3 (1 điểm): Cho phương trình 2 x   m   2 2
5 x  m 16  0 với m là tham số. Tìm m để
phương trình có 2 nghiệm x , x sao cho 2 2
2x  5x x  2x  10 . 1 2 1 1 2 2 Câu 4 (1 điểm):
Giải phương trình 5x  2 x  3 1   2 x  2x x  2 x Câu 5 (1 điểm): Giải phương trình 2 x  3x  7  3x  9 Câu 6 (1 điểm): Giải phương trình: 2 x  3x  5  x  0 Câu 7 (1 điểm): Giải phương trình: 2
2x  2x 12  x  2x 3 Câu 8 (3 điểm):
Trong mf (Oxy) , cho ba điểm ( A 2;1) ; B(4; 4) ; C( 2  ; 4  )
a) Chứng minh A, B, C tạo thành tam giác. Tính chu vi tam giác ABC.
b) Tìm D sao cho tứ giác AODC là hình bình hành. Tìm tọa độ tâm I của hình bình hành.
c) Tìm tọa độ trực tâm H của tam giác ABC.
-------------------------------------------------Hết-------------------------------------------------------
Học sinh không được sử dụng tài liệu. Cán bộ coi kiểm tra không được giải thích gì thêm.
Họ và tên học sinh: ………………………………………….Lớp: …………… SBD:………..…………
Đề Toán khối 10 gồm có 1 trang Page 1/1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020 THÀNH PHỐ HỒ CHÍ MINH MÔN TOÁN – KHỐI 10 TRƯỜNG THPT THỦ THIÊM
Thời gian làm bài 90 phút ĐỀ CHÍNH THỨC Câu 1 (1 điểm):
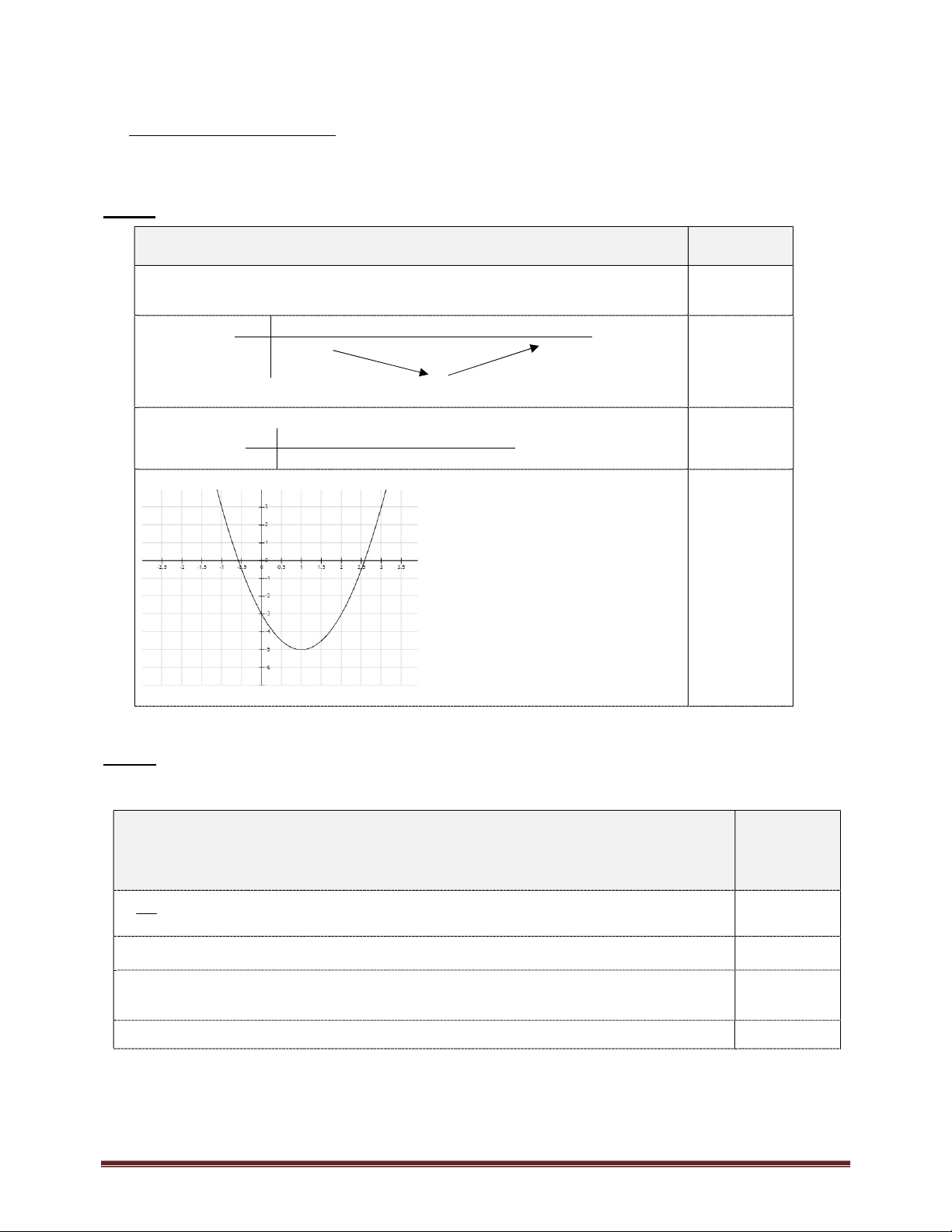
Khảo sát sự biến thiên và vẽ đồ thị hàm số 2 y  2x  4x  3 (1,0đ) TXĐ D=R Đỉnh S 1;5 0.25đ BBT x  1  y   -5 0.25đ
Hàm số tăng trên 1; và giảm trên  ;   1 ng giá trị x -1 0 1 2 3 0.25đ y 3 -3 -5 -3 3 Đồ thị 0.25đ
Parabol nhận đường thẳng x  1 làm trục đối xứng
Câu 2 (1 điểm): Tìm hàm số 2
y  ax  bx  8 biết đồ thị của hàm số là một parabol có đỉnh S 3;17 Tìm hàm số 2
y  ax  bx  8 biết đồ thị của hàm số là một parabol có đỉnh (1,0đ) S  3  ;17  b  3   6a  b  0 (1) 0.25đ 2a a  2
3  b 3  8  17  9a  3b  9 (2) 0.25đ a   (1)(2) suy ra  1 b  6 0.25đ
Vậy hàm số cần tìm là 2 y  x  6x  8 0.25đ
Đề Toán khối 10 gồm có 1 trang Page 2/1
Câu 3 (1 điểm): Cho phương trình 2 x   m   2 2
5 x  m 16  0 với m là tham số. Tìm m
để phương trình có 2 nghiệm x , x sao cho 2 2
2x  5x x  2x  10 . 1 2 1 1 2 2 Cho phương trình 2 x   m   2 2
5 x  m 16  0 , ( m là tham số).
Tìm m để phương trình có 2 nghiệm x , x sao cho 1 2 (1,0đ) 2 2 2x  5x x  2x  1  0. 1 1 2 2   20m  89 0.25đ 89
Phương trình có 2 nghiệm  m  0.25đ 20
Định lý Viet: S  2m  5 và 2 P  m 16 2 2 2x  5x x  2x  1  0 1 1 2 2 0.25đ   2 2 S  2P  5P  1  0 2  9m  40m  44  0 m  2  N    0.25đ 22 m  N   9
Câu 4 (1 điểm): Giải phương trình 5x  2 x  3 1   2 x  2x x  2 x x  0 ĐK:  0,25 x  2 x  0 l
PT  5x  2 x  x  3  x  2 0, 25 2
 x  7x  0 0, 25   0,25 x  7  n
Câu 5 (1 điểm): Giải phương trình 2 x  3x  7  3x  9 3x-9  0 x  3 x  3    2 x +3x-7=3x-9 0,5 2    x  2  0 vn  x  2  l      TN S   0, 25 :  0,25  2 2  x +3x-7=-3x+9  x  6x 16  x  8  l
Câu 6 (1 điểm): Giải phương trình: 2 x  3x  5  x  0 2 x  3x  5  x  0  2 x  3x  5  x 5  x  0
  2x 3x 5x x  5   x   1N  x    5N
Đề Toán khối 10 gồm có 1 trang Page 3/1
Câu 7 (1 điểm): Giải phương trình: 2
2x  2x 12  x  2x 3 2
2x  2x 12  x  2x 3  2 2
x  x 12  2x  x 6
Câu 8 (3 điểm): Trong mf (Oxy) , cho ba điểm ( A 2;1) ; B(4;4) ; C( 2  ; 4  )
a) Chứng minh A, B, C tạo thành tam giác. Tính chu vi tam giác ABC.
b) Tìm D sao cho tứ giác AODC là hình bình hành. Tìm tọa độ tâm I của hình bình hành.
c) Tìm tọa độ trực tâm H của tam giác ABC. a)  AB  (2;5)  AB  29 AC  (4; 3) AC  5  BC  (6; 8  ) BC 10 2 5   Thấy 
 AB, AC không cùng phương  , A B,C tạo thành tam giác 4  3 Chu vi: 15  29 b)   OA  DC
 (2;1)  (2  x ; 4   y ) D D 2  x  2 x  4  D D     4  y  1  y  1   D  D  D(4;3)
Tâm I của hình bình hành là trung điểm OC . Ta có: I (1;2) c) H là trực tâmABC   AH  BC AH.BC  0  
   BH  AC BH.AC  0  106  3  x  4y  2 x  H H H  7     4x  3y  28 76  H H  y   H  7 106 76  H ( ;  ) 7 7
-------------------------------------------------Hết-------------------------------------------------------
Đề Toán khối 10 gồm có 1 trang Page 4/1