Đề thi HK1 Toán 10 năm học 2017 – 2018 trường THPT Hậu Lộc 4 – Thanh Hóa

Đề thi HK1 Toán 10 năm học 2017 – 2018 trường THPT Hậu Lộc 4 – Thanh Hóa gồm 12 câu hỏi trắc nghiệm và 5 bài toán tự luận, thời gian làm bài 60 phút, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trường THPT Hậu Lộc 4 ĐỀ KIỂM TRA HỌC KỲ I NĂM 2017 - 2018
Tổ: Toán - tin Môn : Toán 10
Thời gian làm bài : 60 phút
(Đề bài có 2 trang, gồm 12 câu trắc nghiệm và 5 câu tự luận)
I. Phần trắc nghiệm khách quan (3,0 điểm)
Câu 1: Mệnh đề phủ định của mệnh đề: "Î + +>
2
,50xRx x là
A. $Î + + £
2
,50xRx x B. £ 5x
C. $Î + + <
2
,50xRx x D. "Î + + <
2
,50xRx x
Câu 2: Cho
{}
= 2; 3; 5; 6; 7A ,
{}
= 6; 8B . Tập hợp ÇABlà
A.
{}
2; 8 B.
{}
2; 3; 5; 6; 7; 8 C.
{}
2; 6 D.
{}
6
Câu 3: Số tập con của tập
{}
4; 5; 3A = là:
A. 6 B. 8 C. 5 D. 7
Câu 4: Cho parabol (P) có phương trình =-+
2
24yx x . Tìm điểm mà parabol đi qua.
A. P(4;0) B. N -(3;1) C. M -(3;19) D. Q(4;2)
Câu 5: Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây.
A.
=-+
2
45yx x
. B.
=-+
2
21yx x
. C.
=- + -
2
43yx x
. D.
=--
2
45yx x
.
Câu 6: Cho hàm số =++
2
yax bxc có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
A. ><>0, 0, 0abc . B. >>>0, 0, 0abc. C. >=>0, 0, 0abc. D. <>>0, 0, 0abc.
Câu 7: Cho phương trình +=62 3.x Tính tổng tất cả các nghiệm của phương trình.
A.
9
2
-
B. 6 C.
3
2
-
D. 6-
Câu 8: Cho
1
x và
2
x là hai nghiệm của phương trình --=
22
2017 2017 1 0.xx Tính =+
12
.Sx x
A.
1
2017
S = B.
2017S =-
C.
2017S =
D.
1
2017
S =-
Câu 9: Cho hình bình hành .ABCD Đẳng thức nào đúng?
A. =+
  
AC AB AD B. +=
  
AC BC AB
C. -=
 
2AC BD CD D. -=
  
AC AD CD
Câu 10: Cho
()()
=- =-
3; 4, 1;2.ba Tọa độ của
a
+
b
là:
A.
()
-4; 6 B.
()
-2; 2 C.
()
-4; 6 D.
()
--3; 8
Câu 11: Cho hình vuông ABCD cạnh a . Tính | -

AB AC | theo a.
A. 0 B. 2a C. a D.
2
a
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(–1; 2) và B(3; –4). Tọa độ của vectơ

AB
là
A
. (–4; 6) B. (4; –6) C. (2; –3) D. (3; –2)
II. Phần tự luận (7,0 điểm)
Câu 1 ( 1,0 điểm). Tìm tập xác định của hàm số sau:
a.
21
2
x
y
x
b.
()
--
=+-
-
23 1
6
5
xx
yx
x
Câu 2 ( 1,0 điểm). Xét tính đồng biến, nghịch biến của hàm số =--
2
23yx x .
Câu 3 ( 2,0 điểm). Giải phương trình sau:
a.
3123xx
b.


4
2
13 2 70xxx
Câu 4 ( 1,0 điểm). Giải hệ phương trình:
32 2
2
2429
23 6
xxyxy y
xxy


Câu 5 ( 2,0 điểm).
a. Trong mặt phẳng với hệ tọa độ Oxy , Cho tam giác
ABC
có
-- -(2;1), ( 1; 2), ( 3;2)AB C
. Tìm tọa
độ điểm D sao cho tứ giác
ABCD
là hình bình hành.
b. Cho tam giác
ABC . Gọi M, N là các điểm thỏa mãn: ==
   
1
, 2
3
AM AB CN BC . Chứng minh
rằng :
=- +
  
7
3
3
MN AB AC .
..............................Hết.................................
Họ và Tên:................................................................................; Số báo danh:.....................
Học sinh không được sử dụng tài liệu; Cán bộ xem thi không được giải thích gì thêm!
ĐÁP ÁN ĐỀ THI HỌC KỲ I NĂM 2017 - 2018
MÔN TOÁN 10
I. Phần trắc nghiệm khách quan( 3.0 điểm)
(HS Làm đúng mỗi câu được 0.25 điểm)
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6
A D B C A A
Câu 7 Câu 8 Câu 9 Câu 10 Câu 11 Câu 12
D C A B C B
II. Phần tự luận (7.0 điểm)
Câu Ý Nội Dun
g
Điểm
1 1.0
a
Tìm tập xác định của hàm số sau:
21
2
x
y
x
0.5
ĐK : 20 2xx
0.25
TXĐ: DR \{2}
0.25
b
Tìm tập xác định của hàm số sau:
()
--
=+-
-
23 1
6
5
xx
yx
x
0.5
ĐK:
10
60
50
x
x
x



1
16
6
5
5
x
x
x
x
x



0.25
TXĐ:
1; 6D \{5}
0.25
2
Xét tính đồng biến, nghịch biến của hàm số
=--
2
23yx x
1.0
Tập xác định = D .
Tọa độ đỉnh:
ì
ï
ï
=-
ì
ï
ï
=
ï
ï
ï
íí
ïï
D=-
ïï
î
=-
ï
ï
ï
î
1
2
4
4
b
x
x
a
y
y
a
()
-1; 4I .
0.5
Bảng biến thiên
0.25
Hàm số đồng biến trên khoảng
()
+¥1; ; nghịch biến trên khoảng
()
-¥;1 .
0.25
x

1


4

3 Giải phươn
g
t
r
ình sau: 2,0
a
3123xx
1.0
Ta có pt
3123
31 23
xx
x
x


0.5
2
4
5
x
x

. Vậy phương trình đã cho có hai nghiệm phân biệt là
4
2;
5
xx
0.5
b


4
2
13 2 70xxx
1.0
pt


4
2
13 2140xxx

42
13 140xx
0.25
đặt

2
1tx
( đk
0t ). Ta có phương trình:
2
340tt
0.25
1
4
t
t

, đối chiếu với đk ta được
4t
0.25
Với

2
12 3
414
12 1
xx
tx
xx






KL: phương trình đã cho có hai nghiệm phân biệt 3; 1xx
0.25
4
Giải hệ phương trình:
32 2
2
2429
23 6
xxyxy y
xxy


1.0
Ta có hpt




2
2
22 9
22 6
xyxy
xy xy


0.25

2
2
23 2 3
23
23
32
xx
xy
xy
yx






2
430
32
xx
yx


0.5
1
1
x
y
hoặc
3
3
x
y

.
KL: Hệ phương trình đã cho có nghiệm là:
1
1
x
y
;
3
3
x
y

0.25
5 a Trong mặt phẳng với hệ tọa độ Oxy , Cho tam giác ABC có
-- -(2;1), ( 1; 2), ( 3;2)AB C . Tìm tọa độ điểm D sao cho tứ giác ABCD là
hình bình hành.
1.0
Gọi =---

(;) (3;2)Dxy DC x y
Ta có: ABCD là hình bình hành =
 
AB DC .
0.5
ìì
ïï
-- =- =
ïï

íí
ïï
-=- =
ïï
îî
33 0
(0;5)
23 5
xx
D
yy
0.5
b Cho tam giác ABC . Gọi M, N là các điểm thỏa mãn:
1.0
==
   
1
, 2
3
AM AB CN BC . Chứng minh rằng : =- +
  
7
3
3
MN AB AC .
Từ giả thiết ta có:
()
=-= -=-
        
22 32CN BC AN AC AC AB AN AC AB
0.5
Khi đó
=- = - -
     
1
32
3
MN AN AM AC AB AB =- +
  
7
3
3
MN AB AC
(ĐPCM)
0.5
A
B
C
N
M
.
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Hậu Lộc 4 ĐỀ KIỂM TRA HỌC KỲ I NĂM 2017 - 2018
Tổ: Toán - tin Môn : Toán 10
Thời gian làm bài : 60 phút
(Đề bài có 2 trang, gồm 12 câu trắc nghiệm và 5 câu tự luận)
I. Phần trắc nghiệm khách quan (3,0 điểm)
Câu 1: Mệnh đề phủ định của mệnh đề: "x Î 2 ,
R x + x + 5 > 0 là A. $x Î 2 ,
R x + x + 5 £ 0 B. x £ 5 C. $x Î 2 ,
R x + x + 5 < 0 D. "x Î 2 ,
R x + x + 5 < 0
Câu 2: Cho A = {2;3;5;6;7} , B = {6;8}. Tập hợp A Ç B là A. {2;8} B. {2;3;5;6;7;8} C. {2; } 6 D. { } 6
Câu 3: Số tập con của tập A = {4;5; } 3 là:
A. 6 B. 8 C. 5 D. 7
Câu 4: Cho parabol (P) có phương trình y = 2
x - 2x + 4 . Tìm điểm mà parabol đi qua. A. P(4;0) B. N - ( 3;1) C. M - ( 3;19) D. Q(4;2)
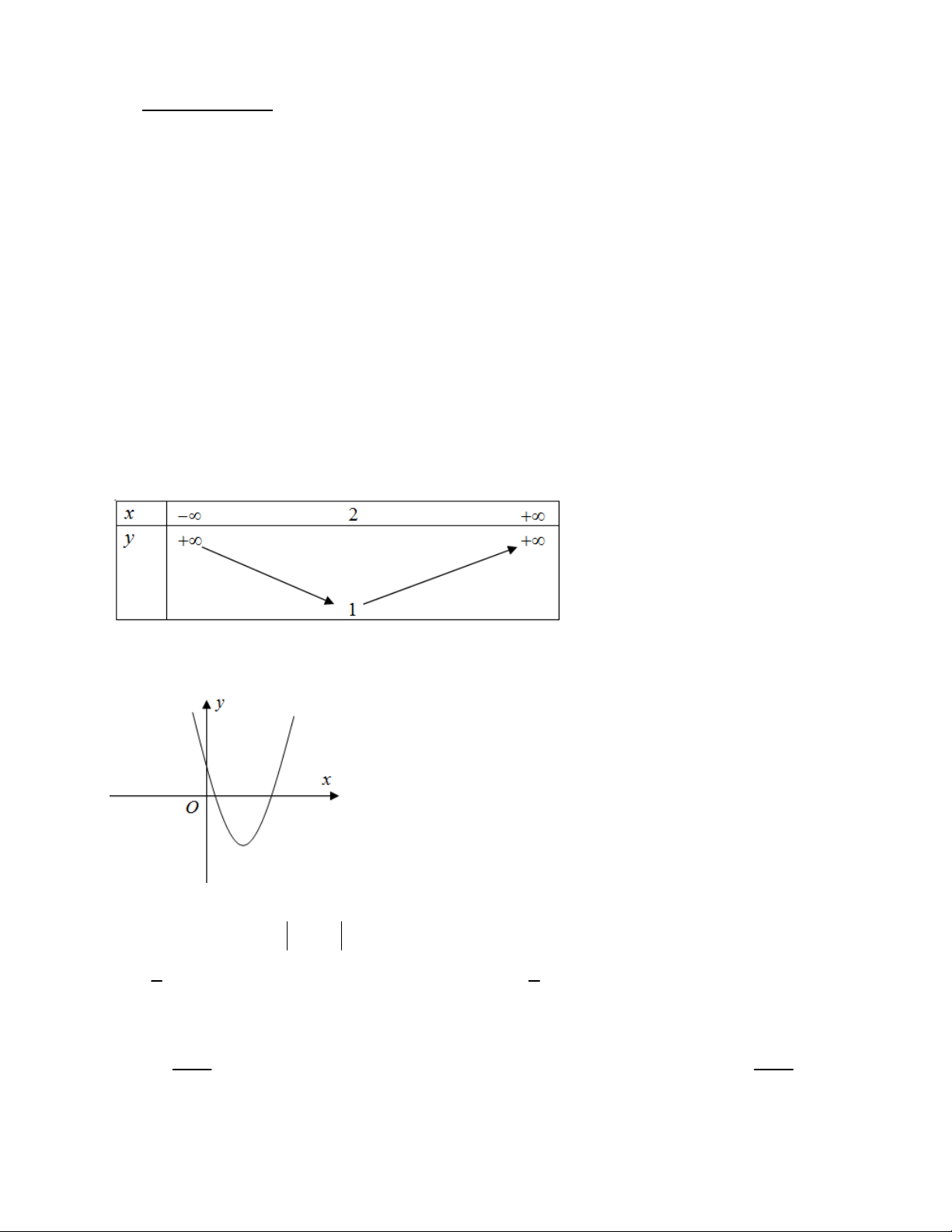
Câu 5: Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây. A. y = 2 x - 4x + 5 . B. y = 2 x - 2x + 1. C. y = - 2
x + 4x - 3 . D. y = 2 x - 4x - 5 . Câu 6: Cho hàm số = 2 y
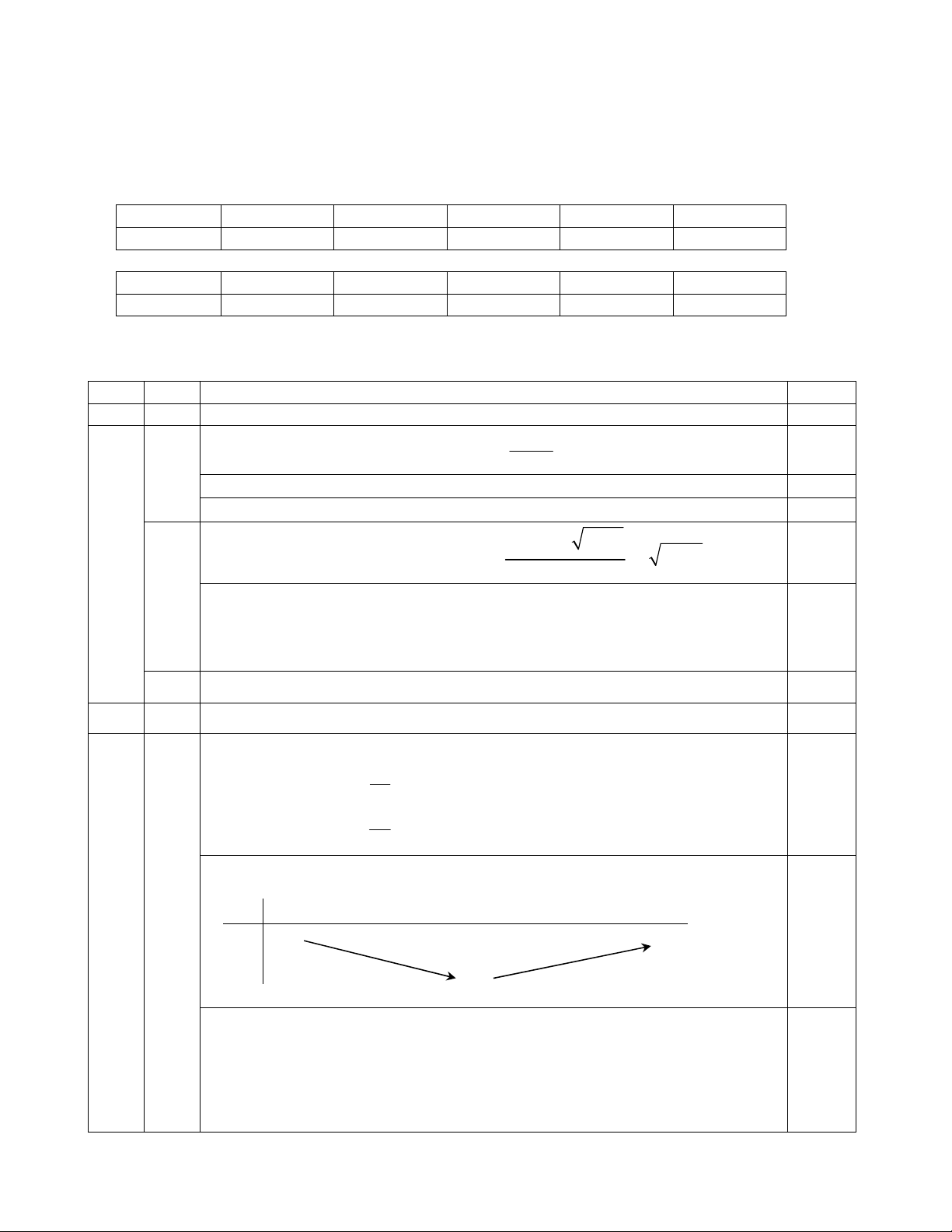
ax + bx + c có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
A. a > 0,b < 0,c > 0 . B. a > 0,b > 0,c > 0 . C. a > 0,b = 0,c > 0 . D. a < 0,b > 0,c > 0 .
Câu 7: Cho phương trình 6 + 2x = 3. Tính tổng tất cả các nghiệm của phương trình. 9 3 A. - B. 6 C. - D. -6 2 2
Câu 8: Cho x và x là hai nghiệm của phương trình 2 x - 2 2017
2017 x - 1 = 0. Tính S = x + x . 1 2 1 2 1 1 A. S = B. S = -2017 C. S = 2017 D. S = - 2017 2017
Câu 9: Cho hình bình hành ABCD. Đẳng thức nào đúng?      
A. AC = AB + AD
B. AC + BC = AB      
C. AC - BD = 2CD
D. AC - AD = CD    
Câu 10: Cho a = (3;-4),b = (-
1;2). Tọa độ của a +b là: A. (-4;6) B. (2;-2) C. (4;-6) D. (-3;-8)  
Câu 11: Cho hình vuông ABCD cạnh a . Tính |AB - AC | theo a. A. 0 B. 2 a a C. a D. 2 
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(–1; 2) và B(3; –4). Tọa độ của vectơ AB là
A. (–4; 6) B. (4; –6) C. (2; –3) D. (3; –2)
II. Phần tự luận (7,0 điểm)
Câu 1 ( 1,0 điểm). Tìm tập xác định của hàm số sau: 2x 1 a. y x  2 (2x - 3) x -1 b. y = + 6 - x x - 5
Câu 2 ( 1,0 điểm). Xét tính đồng biến, nghịch biến của hàm số y = 2 x - 2x - 3 .
Câu 3 ( 2,0 điểm). Giải phương trình sau:
a. 3x 1  2x  3
b.  x  4   2 1
3 x  2x  7  0 3 2 2
2x x y  4xy  2y  9
Câu 4 ( 1,0 điểm). Giải hệ phương trình:  2
x  2x  3y  6 Câu 5 ( 2,0 điểm).
a. Trong mặt phẳng với hệ tọa độ Oxy , Cho tam giác ABC có ( A 2;1),B - ( 1;-2),C - ( 3;2) . Tìm tọa
độ điểm D sao cho tứ giác ABCD là hình bình hành.     1
b. Cho tam giác ABC . Gọi M, N là các điểm thỏa mãn: AM = AB, CN = 2BC . Chứng minh 3    7
rằng :MN = - AB + 3AC . 3
..............................Hết.................................
Họ và Tên:................................................................................; Số báo danh:.....................
Học sinh không được sử dụng tài liệu; Cán bộ xem thi không được giải thích gì thêm!
ĐÁP ÁN ĐỀ THI HỌC KỲ I NĂM 2017 - 2018 MÔN TOÁN 10
I. Phần trắc nghiệm khách quan( 3.0 điểm)
(HS Làm đúng mỗi câu được 0.25 điểm) Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 A D B C A A Câu 7 Câu 8 Câu 9 Câu 10 Câu 11 Câu 12 D C A B C B
II. Phần tự luận (7.0 điểm) Câu Ý Nội Dung Điểm 1 1.0 a 2x 1
Tìm tập xác định của hàm số sau: y x  2 0.5
ĐK : x  2  0  x  2 0.25
 TXĐ: D R \{2} 0.25 b (2x - 3) x -1
Tìm tập xác định của hàm số sau: y = + 6 - x 0.5 x - 5 x 1  0 x  1   1   x  6 ĐK:
6  x  0  x  6     x  5 0.25 x  5  0  x  5 
 TXĐ: D  1;6 \{5} 0.25 2
Xét tính đồng biến, nghịch biến của hàm số y = 2 x - 2x - 3 1.0
Tập xác định D =  . ìï ï b ïx = - ìïx = 1 Tọa độ đỉnh: ï 2a ï í  í  I (1; - 4). ï D ïy = - ï ï 4 ïy = - î ï 0.5 ïî 4a Bảng biến thiên x  1    y 4  0.25
Hàm số đồng biến trên khoảng (1; + )
¥ ; nghịch biến trên khoảng (-¥; )1. 0.25 3 Giải phương trình sau: 2,0 a
3x 1  2x  3 1.0
3x 1  2x  3 Ta có pt   3 0.5 x 1  2  x  3 x  2    4
. Vậy phương trình đã cho có hai nghiệm phân biệt là x  5 4 0.5 x  2;  x  5 b
x  4   2 1
3 x  2x  7  0 1.0 pt   4 2 x  4   2 1
3 x  2x  
1  4  0   x   1  3 x   1  4  0 0.25
đặt t   x  2
1 ( đk t  0 ). Ta có phương trình: 2
t  3t  4  0 0.25 t  1   
, đối chiếu với đk ta được t  4  0.25 t  4 x   x
Với t    x  2 1 2 3 4 1  4      x 1  2  x  1  0.25
KL: phương trình đã cho có hai nghiệm phân biệt x  3; x  1 4 3 2 2
2x x y  4xy  2y  9
Giải hệ phương trình:  1.0 2
x  2x  3y  6  2  x  2y
2xy  9 Ta có hpt  0.25  2  x  2y
2xy  6 2 2
x  2y  3
x  23 2x  3 2
x  4x  3  0       0.5
2x y  3
y  3 2x
y  3  2xx 1 x  3   hoặc  .  y  1 y  3 
x  1 x  3
KL: Hệ phương trình đã cho có nghiệm là:  ;  0.25
y 1 y  3  5 a
Trong mặt phẳng với hệ tọa độ Oxy , Cho tam giác ABC có ( A 2;1),B - ( 1;-2),C -
( 3;2) . Tìm tọa độ điểm D sao cho tứ giác ABCD là 1.0
hình bình hành. 
Gọi D(x;y)  DC = - ( 3 - x;2 - y)   0.5
Ta có: ABCD là hình bình hành  AB = DC . ìï ì -3 - x = -3 ïx = ï ï 0  í  í  D(0;5) ï 0.5 2 - y = -3 ïy = ïî ïî 5 b
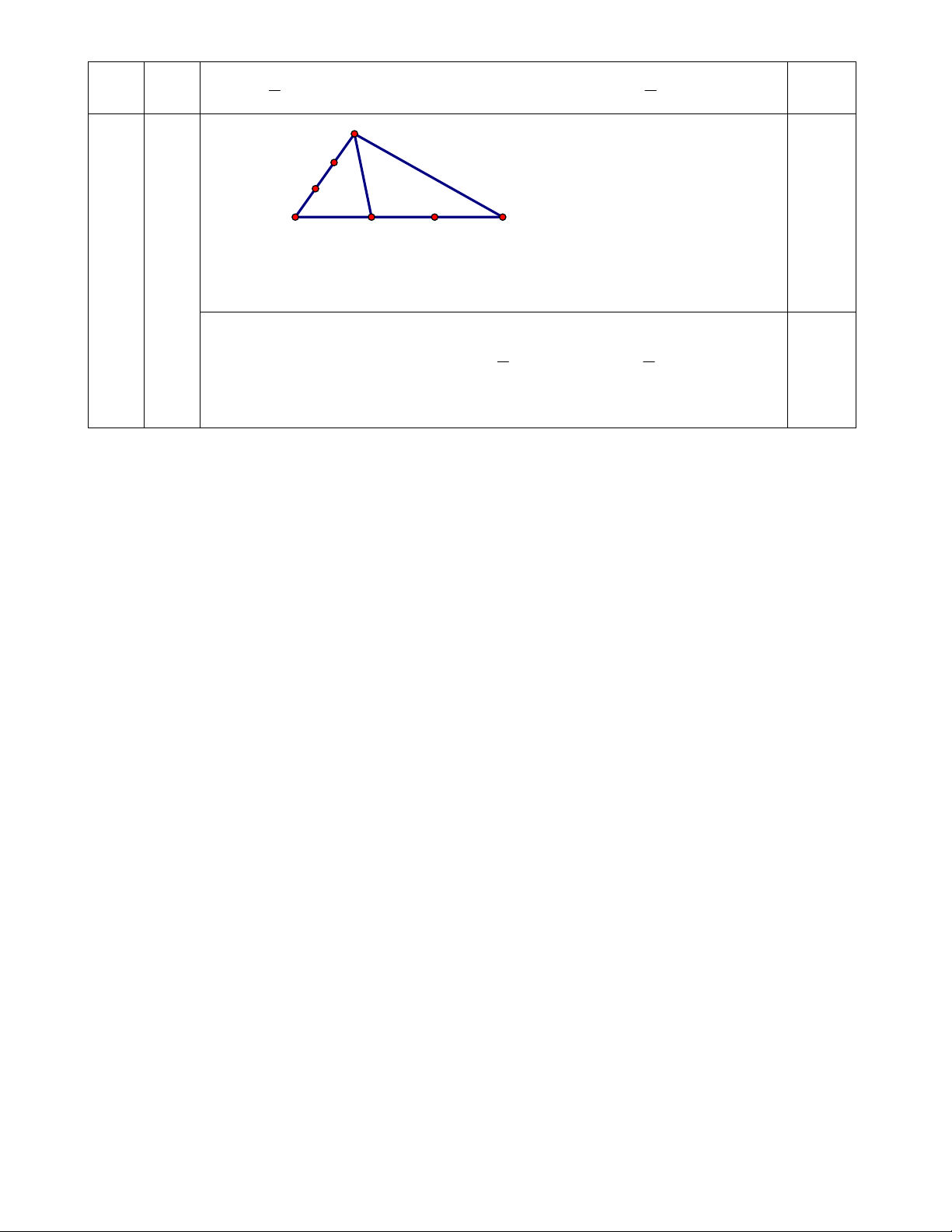
Cho tam giác ABC . Gọi M, N là các điểm thỏa mãn: 1.0     1    7
AM = AB, CN =
2BC . Chứng minh rằng :MN = - AB + 3AC . 3 3 A M B C N 0.5 Từ giả thiết ta có:         
CN = 2BC AN - AC = 2(AC - AB)  AN = 3AC - 2AB Khi đó       1    7
MN = AN - AM = 3AC - 2AB - AB MN = - AB + 3AC  3 3 (ĐPCM) 0.5 .