SỞ GD&ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán 10 (Nâng cao)
Thời gian làm bài: 90 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC ĐỀ: 1
Câu 1: (2,0 điểm). Giải các phương trình sau:
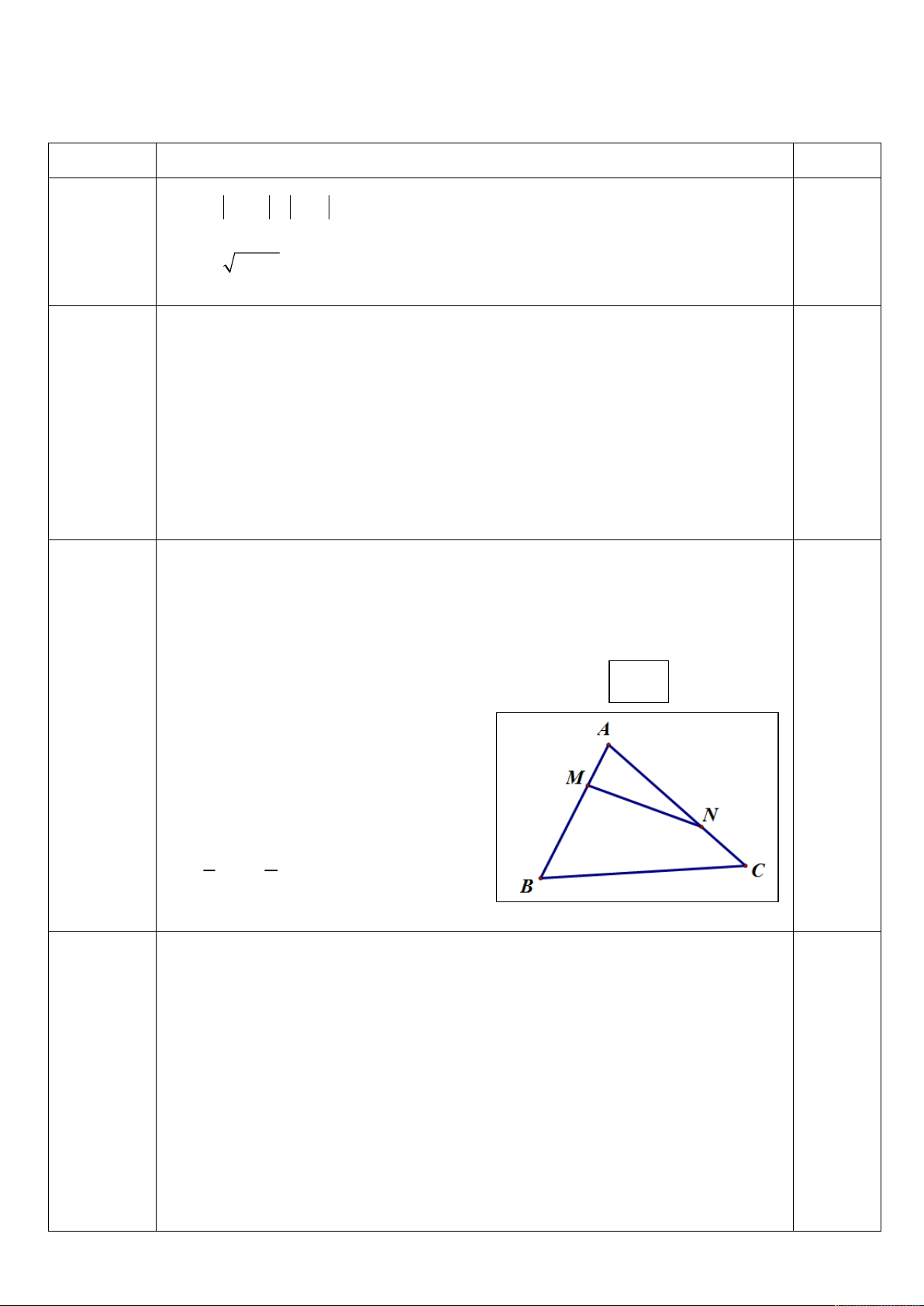
a) 2x 1  x  2
b) 4x  3  x
Câu 2: (2,0 điểm). Cho phương trình 2
x  2 x  m  5  0 (m là tham số).
a) Giải phương trình khi m = 2.
b) Tìm tất cả các giá trị của tham số m để phương có hai nghiệm phân biệt x , x thỏa 1 2 mãn 2 2
x  x  20 . 1 2 Câu 3: (2,0 điểm) x  y  3
a) Giải hệ phương trình  2 2
x  y  xy  3     
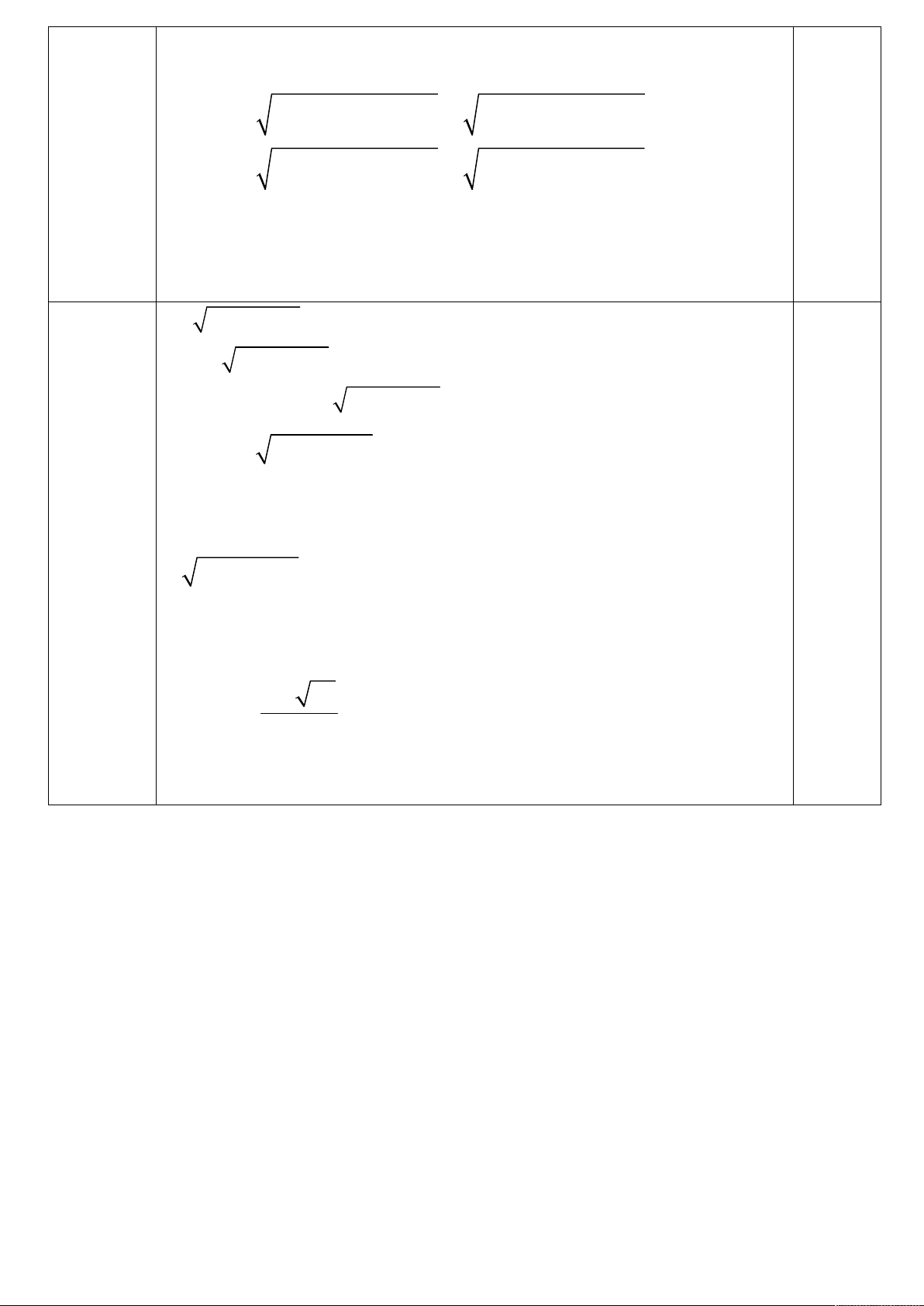
b) Cho tam giác ABC. Gọi M và N là hai điểm thỏa mãn AB  3AM , AN  2NC .   
Hãy biểu thị MN theo hai vectơ AB, AC .
Câu 4: (3,0 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;4), B(4;1), C(0;1).
a) Xác định tọa độ điểm D để tứ giác ABCD là hình bình hành.
b) Xác định tọa độ trực tâm H của tam giác ABC.
c) Xác định tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.
Câu 5: (1,0 điểm) Giải phương trình 3 2 3 2
2 x  3x  3  8x 13x  7 . x
-----------------HẾT---------------------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh:…………………………..Lớp:………….Số báo danh:……………….
Chữ ký của giám thị:………………………………….
SỞ GD&ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán 10 (Nâng cao)
Thời gian làm bài: 90 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC ĐỀ: 2
Câu 1: (2,0 điểm). Giải các phương trình sau:
a) 2x 1  x  2
b) 3x  2  x
Câu 2: (2,0 điểm). Cho phương trình 2
x  2 x  m  5  0 (m là tham số).
a) Giải phương trình khi m = -8.
b) Tìm tất cả các giá trị của tham số m để phương có hai nghiệm phân biệt x , x thỏa 1 2 mãn 2 2
x  x  20 . 1 2 Câu 3: (2,0 điểm) x  y  3
a) Giải hệ phương trình  2 2
x  y  xy  7     
b) Cho tam giác ABC. Gọi M và N là hai điểm thỏa mãn AM  3MB, AC  2 AN .   
Hãy biểu thị MN theo hai vectơ AB, AC .
Câu 4: (3,0 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4;1), B(0;1), C(1;4).
a) Xác định tọa độ điểm D để tứ giác ABCD là hình bình hành.
b) Xác định tọa độ trực tâm H của tam giác ABC.
c) Xác định tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.
Câu 5: (1,0 điểm) Giải phương trình 3 2 3 2
2 x  3x  3  8x 13x  7 . x
-----------------HẾT---------------------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh:…………………………..Lớp:………….Số báo danh:……………….
Chữ ký của giám thị:…………………………………. HƯỚNG DẪN CHẤM ĐỀ 1 Câu NỘI DUNG ĐIỂM 1a: 1đ
2x 1  x  2 x  1  0,5+0,5
a) 2x 1  x  2     1b: 1đ
2x 1  2  x x  1   x  0 x  1
b) 4x  3  x    0,5+0,5 2 
x  4x  3  0 x  3   Câu 2 a) Thay m = 2, ta có pt 2
x  2 x  3  0 0,5 2a: 1  x   1 điểm   x  0,5  3 2b: 1 điểm
b) Đk có hai nghiệm ∆ = 6 − ≥ 0 <=> ≤ 6 0,25 Theo định lí Viet: + = 2; = − 5 0,25
Ycbt  (x1+x2)2 – 2x1x2 = 20  4 – 2(m – 5 ) =20 m = - 3 (TM) 0,5 Câu 3 x  y  3
 y  3  x a)    a) 1 điểm 2 2 2 2
x  y  xy  3
x  (3  x)  x(3  x)  3   0,25
 y  3  x   2
3x  9x  6  0 0,25  A x  1 x  2   v  0,5 y  2 y  1      
b) AB  3AM , AN  2NC .
  
MN  MA  AN 0,5 1  2    AB  AC 3 3 0,5 Câu 4
a) A(1;4), B(4;1), C(0;1). Tứ giác ABCD là hbh khi và chỉ khi
x  x  x  x x  3  A C B D D 0,5     D( 3  ; 4) 4a: 1
y  y  y  y y  4 +0,5  A C B D  D điểm  
b) Gọi H(x;y) => AH   x 1; y  4 , BH   x  4; y   1   4b: 1 AC   1  ; 3  , BC   4  ; 0   điểm   AH.BC  0 x  1 0,5  
H là trực tâm khi và chỉ khi     H (1; 2) y  2 BH.AC  0   0,5
c) Gọi I(a;b) là tâm đường tròn ngoại tiếp tam giác ABC Ta có IA =IB =IC 0,25 4c: 1đ
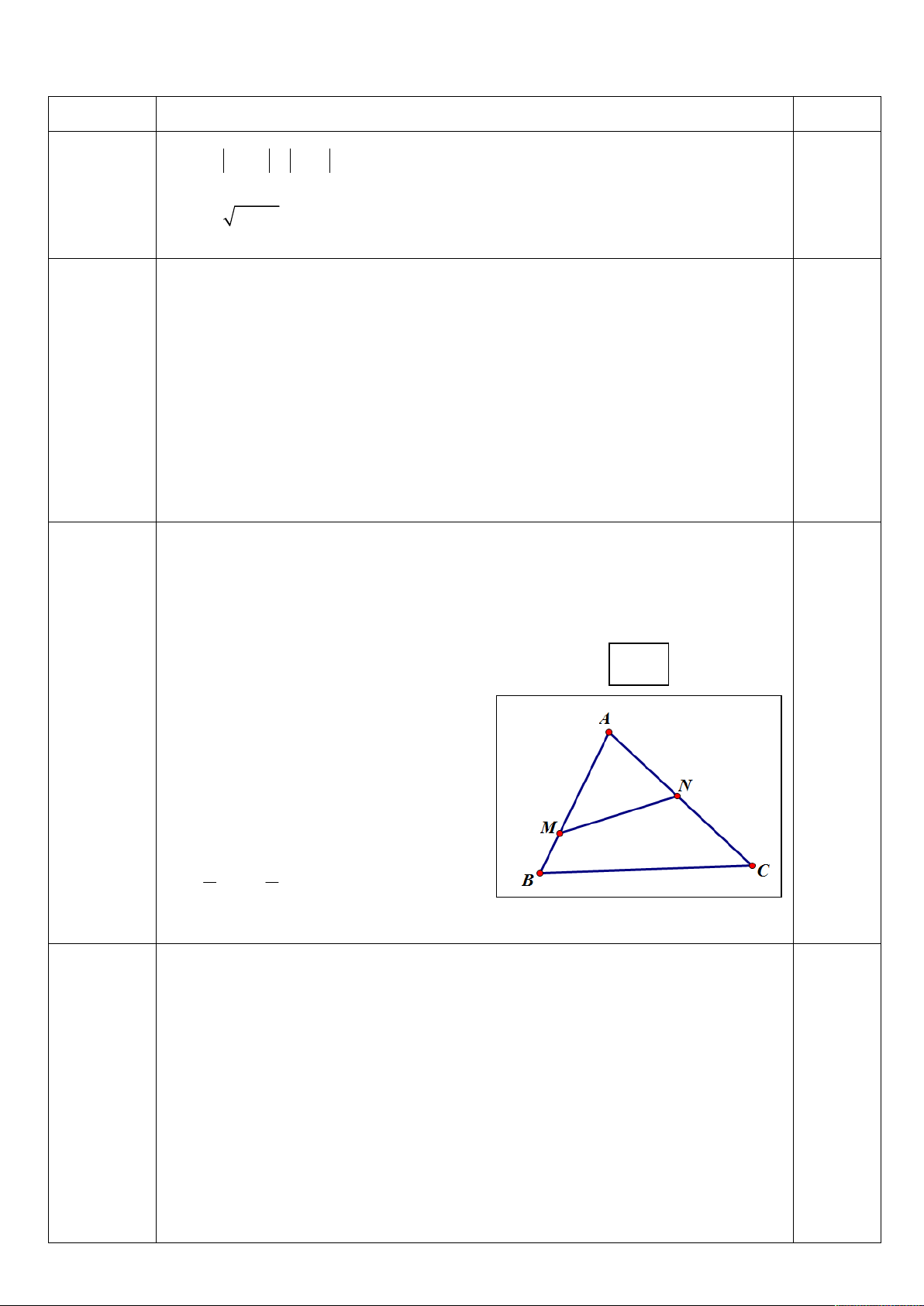
 (a 1)  b  42  (a  4) b  2 2 2 1   
 (a 1)  b  42  (a  0)  b  2 2 2 1  0,25
6a  6b  0  
 a  b  2  I (2; 2) 2a  6b  16  0,5 Câu 5 3 2 3 2
2 x  3x  3  8x 13x  7 x 1 điểm 3 2 3 2
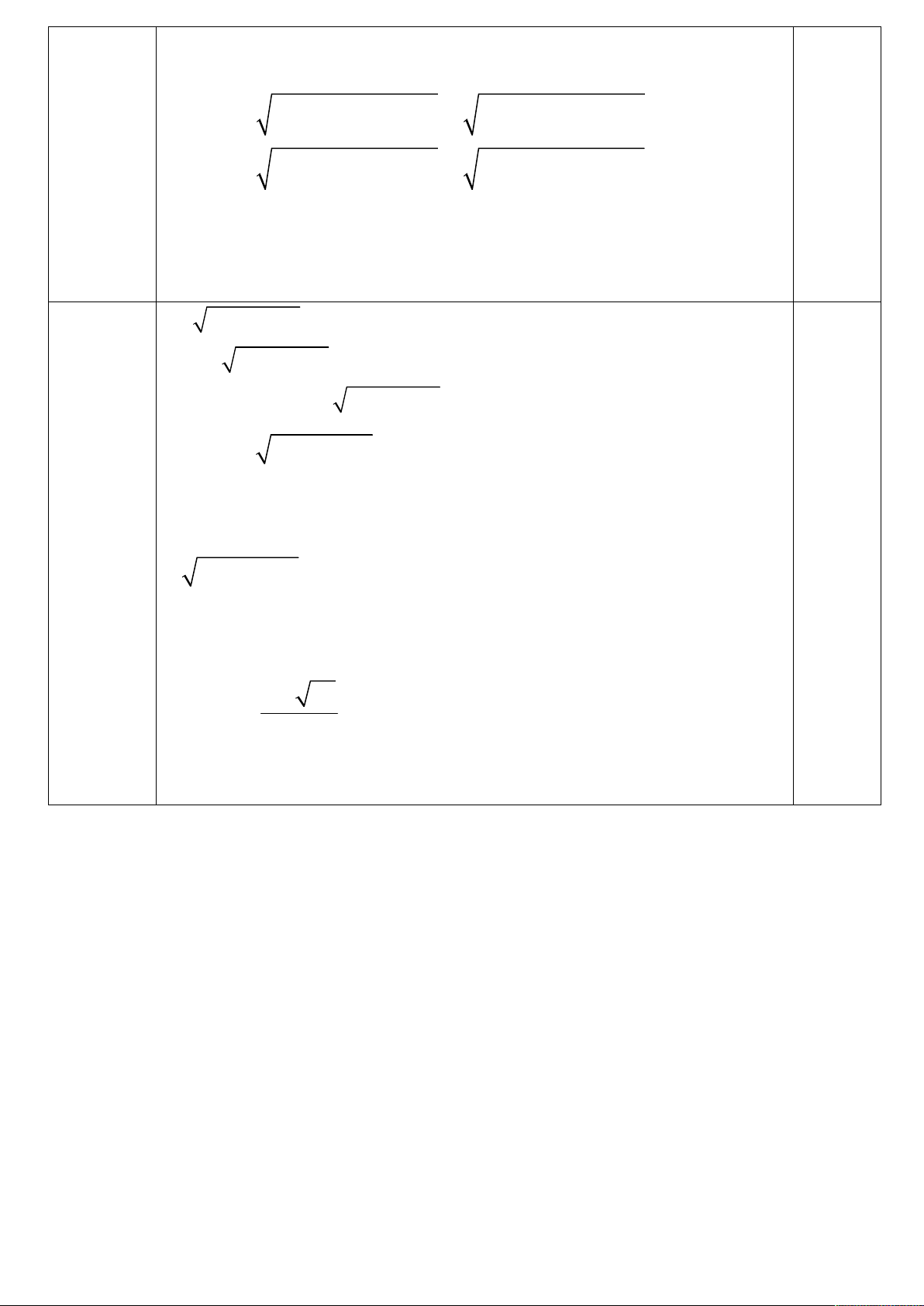
 2 x  3x  3  (2x 1)  x  x  1 2 3 2 3
 x  3x  3  2 x  3x  3  (2x 1)  2(2x 1) 3 2 Đặt a 
x  3x  3, b  2x 1 0,5
Ta có a3+2a =b3+2b  (a-b)(a2 +ab +b2+2) = 0  a = b
(do phương trình a2 +ab +b2+2 = 0 theo ẩn a có delta âm) 3 2 3 2
x  3x  3  2x 1  8x 13x  3x  2  0 2
 (x 1)(8x  5x  2)  0 x  1   5  89 0,5 x   16
(nếu giải cách khác và chỉ tìm được nghiệm bằng 1thì không cho điểm) HƯỚNG DẪN CHẤM ĐỀ 2 Câu NỘI DUNG ĐIỂM 1a: 1đ
2x 1  x  2 x  1 0,5+0,5
a) 2x 1  x  2     1b: 1đ 2x 1  2   x x  1    x  0 x  1
b) 3x  2  x    0,5+0,5 2 
x  3x  2  0 x  2   Câu 2 a) Thay m = -8, ta có pt 2
x  2 x  3  0 0,5 2a: 1  x   1 điểm   x  0,5  3 2b: 1 điểm
b) Đk có hai nghiệm ∆ = −4 − ≥ 0 <=> ≤ −4 0,25 Theo định lí Viet: + = 2; = + 5 0,25
Ycbt  (x1+x2)2 – 2x1x2 = 20  4 – 2(m + 5 )=20m = -13 (TM) 0,5 Câu 3 x  y  3
 y  3  x a)    a) 1 điểm 2 2 2 2
x  y  xy  7
x  (3  x)  x(3  x)  7   0,25
 y  3  x   2
x  3x  2  0 0,25  A x  1 x  2   v  0,5 y  2 y  1      
b) AM  3MB, AC  2 AN . 0,5
  
MN  MA  AN 2  1  0,5   AB  AC 3 2 Câu 4
a) A(4;1), B(0;1), C(1;4). Tứ giác ABCD là hbh khi và chỉ khi
x  x  x  x x  5 A C B D D 0,5     D(5; 4) 4a: 1
y  y  y  y y  4 +0,5  A C B D  D điểm  
b) Gọi H(x;y) => AH   x  4; y   1 , BH   ; x y   1   4b: 1 AC   3
 ;3, BC  1;3   điểm   AH.BC  0 x  1 0,5  
H là trực tâm khi và chỉ khi     H (1; 2) y  2 BH.AC  0   0,5
c) Gọi I(a;b) là tâm đường tròn ngoại tiếp tam giác ABC Ta có IA =IB =IC 0,25 4c: 1đ
 (a 1)  b  42  (a  4) b  2 2 2 1   
 (a 1)  b  42  (a  0)  b  2 2 2 1  0,25
6a  6b  0  
 a  b  2  I (2; 2) 2a  6b  16  0,5 Câu 5 3 2 3 2
2 x  3x  3  8x 13x  7 x 1 điểm 3 2 3 2
 2 x  3x  3  (2x 1)  x  x  1 2 3 2 3
 x  3x  3  2 x  3x  3  (2x 1)  2(2x 1) 3 2 Đặt a 
x  3x  3, b  2x 1 0,5
Ta có a3+2a =b3+2b  (a-b)(a2 +ab +b2+2) = 0  a = b
(do phương trình a2 +ab +b2+2 = 0 theo ẩn a có delta âm) 3 2 3 2
x  3x  3  2x 1  8x 13x  3x  2  0 2
 (x 1)(8x  5x  2)  0 x  1   5  89 0,5 x   16
(nếu giải cách khác và chỉ tìm được nghiệm bằng 1thì không cho điểm)