

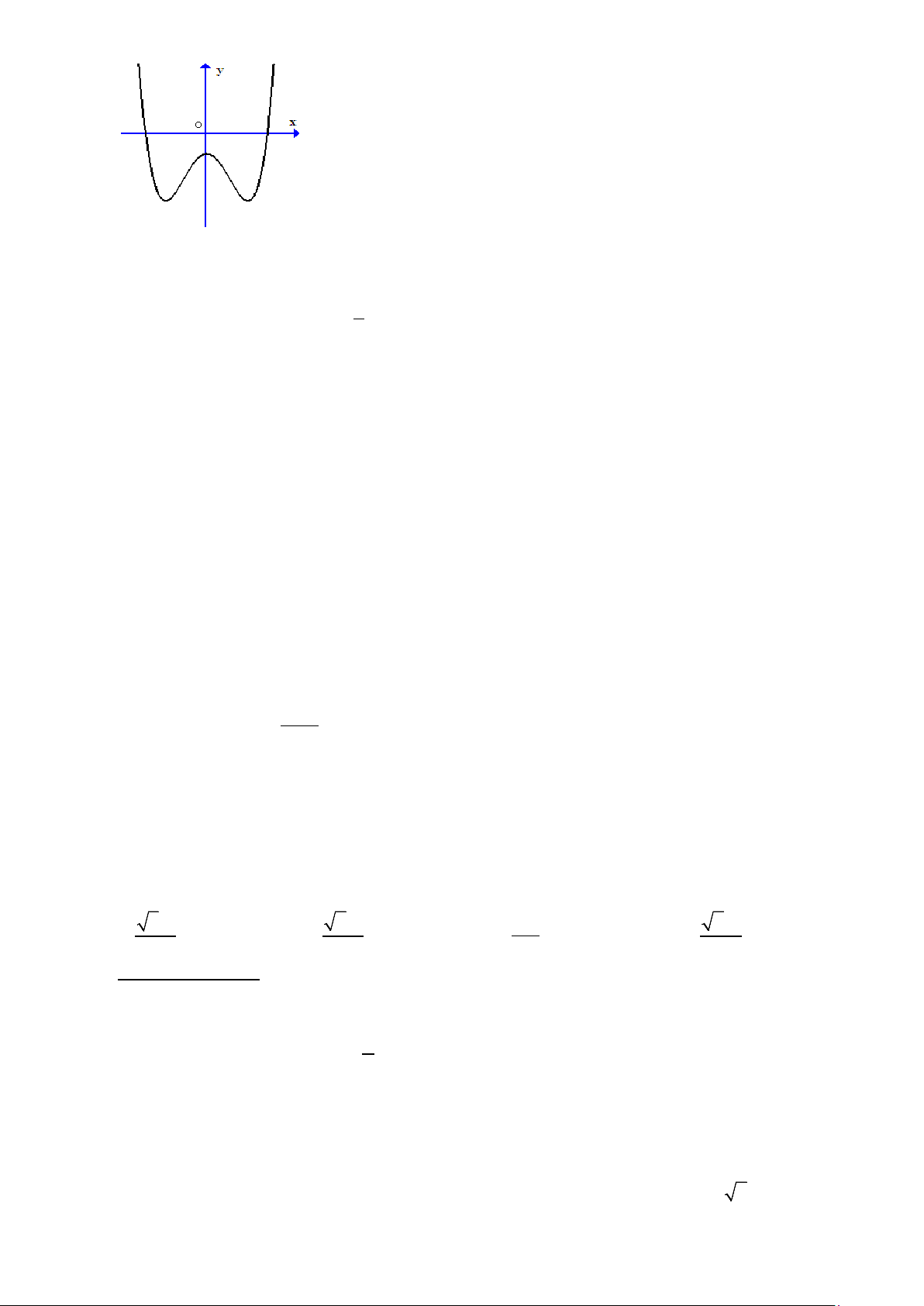


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2019 – 2020
THÀNH PHỐ HỒ CHÍ MINH
Môn : TOÁN – KHỐI 12
Trường THPT Tân Phong
Thời gian làm bài: 90 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC
(30 câu trắc nghiệm và 6 câu tự luận)
I) PHẦN TRẮC NGHIỆM: (6 điểm) Mã đề thi 132
Câu 1: Tất cả các giá trị của m để hàm số y = (m + ) 4 x + (m − ) 2 1 2
2 x +1 có ba cực trị là : A. 1 − ≤ m ≤ 2 . B. m < 1 − . C. m > 2 . D. 1 − < m < 2 .
Câu 2: Cho tam giác ABC vuông tại A , AB = 3a , AC = 4a . Gọi M là trung điểm của AC . Khi quay
quanh AB, các đường gấp khúc AMB , ACB sinh ra các hình nón có diện tích xung quanh lần lượt là S , 1 S S . Tỉ số 1 là: 2 S2 A. S 2 S 1 S 13 S 1 1 = . B. 1 = . C. 1 = . D. 1 = . S 5 S 2 S 10 S 4 2 2 2 2
Câu 3: Cho hình trụ có bán kính đáy bằng 5cm và khoảng cách giữa hai đáy là 7cm . Cắt khối trụ bởi
một mặt phẳng song song với trục và cách trục 3cm . Diện tích S của thiết diện được tạo thành bằng: A. 2 53cm . B. 2 56cm . C. 2 46cm . D. 2 55cm . Câu 4: Cho hàm số 3 2
y = −x − mx + (4m + 9) x + 5, với m là tham số. Có bao nhiêu giá trị nguyên của m
để hàm số nghịch biến trên ( ; −∞ +∞) ? A. 7. B. 5. C. 6. D. 4.
Câu 5: Cho hình chóp SABC có đáy ABC là tam giác vuông cân, AB = AC = a , SC ⊥ ( ABC) và
SC = a . Mặt phẳng qua C và vuông góc với SB cắt ,
SA SB lần lượt tại E và F . Thể tích khối chóp
S.CEF tính theo a là: 3 3 3 3 A. 2 a a = a V . B. V = . C. V = . D. 2 = a V . SCEF 36 SCEF 18 SCEF 36 SCEF 12
Câu 6: Cho khối nón có bán kính r = 5 và chiều cao h = 3. Thể tích V của khối nón là: A. V = 9π 5 . B. V = 3π 5 . C. V = π 5 . D. V = 5π . x −
Câu 7: Cho hàm số f (x) 2
= e . Mệnh đề nào sau đây đúng ? x x A. f ∫ (x) 1 − − 2 dx = e + C . B. f ∫ (x) 2 dx = 2e − + C . 2 x x C. f ∫ (x) − 1 − 2 dx = 2e + C . D. f ∫ (x) 2
dx = − e + C . 2
Câu 8: Phương trình 2x x+2
2 − 3.2 + 32 = 0 có tổng các nghiệm là: A. 2 − . B. 12. C. 6 . D. 5.
Câu 9: Đạo hàm của hàm số = 3x y + log x là : A. x 1 y′ = 3 ln3+ . B. 1 y′ = log x +
. C. y′ = log x + ln3. D. 1 ln x y − ′ = . x ln10 3 x ln3 3 ln3 11 3 7 3 m
Câu 10: Rút gọn biểu thức a .a A =
với a > 0 ta được kết quả n
A = a , trong đó m , n∈* và m 4 7 5 a . a− n
là phân số tối giản. Khẳng định nào sau đây là đúng ? A. 2 2 m − n = 312 − . B. 2 2 m − n = 312 . C. 2 2 m + n = 543. D. 2 2 m + n = 409 .
Trang 1/4 - Mã đề thi 132
Câu 11: Cho hình chóp S.ABC có SA ⊥ ( ABC), A
∆ BC vuông cân tại A, SA = BC = .
a Thể tích V của
khối chóp S.ABC tính theo a là: 3 3 3 A. a a a 3 V = 2a . B. V = . C. V = . D. V = . 2 4 12 2 x −4x
Câu 12: Tập nghiệm S của bất phương trình 1 < 8 là: 2 A. S = ( ; −∞ 3) .
B. S = (1;+∞) . C. S = ( ; −∞ ) 1 ∪(3;+∞) . D. S = (1;3) . 2
Câu 13: Gọi (C) là đồ thị của hàm số x y =
. Phương trình tiếp tuyến của (C) vuông góc với đường 2 − x thẳng 4 y = x +1 là: 3 A. (d ) 3 9 3 1
: y = x − , y = x − . B. (d ) 3 9 3 1
: y = − x − , y = − x − . 4 2 4 2 4 2 4 2 C. (d ) 3 7 3 1
: y = − x − , y = − x − . D. (d ) 3 3
: y = − x, y = − x −1. 4 2 4 2 4 4
Câu 14: Tích hai nghiệm của phương trình 2
log x − 6log x + 8 = 0 bằng: 3 3 A. 8 . B. 6 . C. 729 . D. 90. Câu 15: Cho hàm số 2x −1 y =
(C) và đường thẳng d : y = x + m . Với giá trị nào của tham số m thì 1− x
đường thẳng cắt đồ thị (C) tại hai điểm phân biệt? A. 5 − < m < 1 − . B. m < 5 − . C. m∈( ; −∞ 5 − )∪( 1; − +∞). D. m > 1 − .
Câu 16: Phương trình 2 x−3 x −5x+6 2 = 3
có hai nghiệm x , x trong đó x < x .Hãy chọn phát biểu đúng? 1 2 1 2
A. 3x − 2x = log 8 . B. 2x −3x = log 8 .
C. 2x + 3x = log 54. D. 3x + 2x = log 54. 1 2 3 1 2 3 1 2 3 1 2 3
Câu 17: Tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số 3
y = −x + 3x + 2
tại 3 điểm phân biệt là: A.0 ≤ m < 4 . B.0 < m ≤ 4 .
C. 0 < m < 4 .
D. m < 0;m > 4.
Câu 18: Cho các số thực dương a , b thỏa mãn 3log a + 2logb =1. Mệnh đề nào sau đây đúng? A. 3 2 a + b =1. B. 3 2 a + b =10
C. 3a + 2b =10 . D. 3 2 a b =10 .
Câu 19: Cho khối tứ diện ABCD . Lấy điểm M nằm giữa A và B , điểm N nằm giữa C và D . Bằng
hai mặt phẳng (CDM ) và ( ABN ) , ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
A. MANC , BCMN , AMND , MBND .
B. MANC , BCDN , AMND , ABND .
C. ABCN , ABND , AMND , MBND .
D. NACB , BCMN , ABND , MBND .
Câu 20: Cho hàm số f có đạo hàm là 5
f (x) x x 2 1 x 3
3 . Số điểm cực trị của hàm số f là : A. 1. B. 2 . C. 0 . D. 3.
Câu 21: Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số ( ) 2 3 e x f x − = trên
đoạn [0;2] . Mối liên hệ giữa M và m là :
A. M − m = e. B. M 2 = e .
C. m + M =1. D. 1 . m M = . m 2 e
Câu 22: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 ; SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Thể tích khối chóp S.ABCD tính theo a là: A. 3 3 2a . B. 3 3a . C. 3 6a . D. 3 2a .
Trang 2/4 - Mã đề thi 132 Câu 23: Cho hàm số 4 2
y = ax + bx + c(a ≠ 0) có đồ thị như hình sau.Xác định dấu của a,b,c ? .
A. a > 0,b < 0,c < 0 .
B. a > 0,b > 0,c < 0.
C. a < 0,b < 0,c < 0 .
D. a > 0,b < 0,c > 0.
Câu 24: Cho khối hộp chữ nhật ABC . D A′B C ′ D
′ ′ có thể tích V . Mệnh đề nào sau đây đúng? 1
A. V = A . B BC.AA′.
B. V = A .
B BC.AA′ . C. V = A . B AC.AA′ .
D. V = A . B AC.AD . 3
Câu 25: Tập xác định của hàm số y xπ = + (x − )e 2 1 là: A. (1;+∞). B. ( ; −∞ − )
1 ∪(1;+∞) . C. (0;+∞). D. \{ 1; − } 1 .
Câu 26: Số nghiệm của phương trình log x + log x −1 = 2 là: 2 2 ( ) A. 1. B. 2 . C. 0 . D. 3.
Câu 27: Cho hàm số y = f (x) có lim f (x) = −∞ và lim f (x) = +∞ . Khẳng định nào sau đây là khẳng x 1+ → x 1− →− định đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x =1 và x = 1 − .
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y =1 và y = 1 − .
D. Đồ thị hàm số đã cho không có tiệm cận đứng.
Câu 28: Cho hình chữ nhật ABCD có AB = 4 và AD = 3. Thể tích của khối trụ được tạo thành khi quay
hình chữ nhật ABCD quanh cạnh AB là: A. 48π . B. 36π . C. 12π . D. 24π . Câu 29: Cho hàm số x − 2 y =
. Mệnh đề nào sau đây đúng? x + 3
A. Hàm số nghịch biến trên từng khoảng xác định.
B. Hàm số đồng biến trên từng khoảng xác định.
C. Hàm số nghịch biến trên khoảng ( ; −∞ +∞ ).
D. Hàm số đồng biến trên khoảng ( ; −∞ +∞ ).
Câu 30: Cho lăng trụ đứng tam giác MN . P M N ′ P
′ ′ có đáy MNP là tam giác đều cạnh a , đường chéo
MP′ tạo với mặt phẳng đáy một góc bằng 60°. Thể tích của khối lăng trụ MN . P M N ′ P
′ ′ tính theo a là : 3 3 3 3 A. 3a . B. 2a . C. 3a . D. 2a . 2 3 4 4
II) PHẦN TỰ LUẬN: (4 điểm)
Câu 1: Giải phương trình sau: log x + log x −1 = 2 2 2 ( ) 2 x −4x
Câu 2: Giải bất phương trình sau: 1 < 8 2 Câu 3: Cho hàm số 3 2
y = −x − mx + (4m + 9) x + 5, với m là tham số. Xác định m để hàm số nghịch biến trên tập xác định.
Câu 4: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số ( ) 2 3 e x f x − = trên đoạn [0;2] .
Câu 5: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 ; SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng 60°. Tính thể tích khối chóp S.ABCD theo a .
Trang 3/4 - Mã đề thi 132
Câu 6: Cho tam giác ABC vuông tại A , AB = 3a , AC = 4a . Gọi M là trung điểm của AC . Khi quay
quanh AB, các đường gấp khúc AMB , ACB sinh ra các hình nón có diện tích xung quanh lần lượt là S , 1 S
S . Tính tỉ số 1 . 2 S2 ----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ................................................. Số báo danh:...........................
Chữ kí của giám thị 1: ................................ Chữ kí của giám thị 2: ................................
-----------------------------------------------
Trang 4/4 - Mã đề thi 132
ĐÁP ÁN MÔN TOÁN HKI KHỐI 12 NĂM 2019-2020
I) PHẦN TRẮC NGHIỆM: (6 điểm)
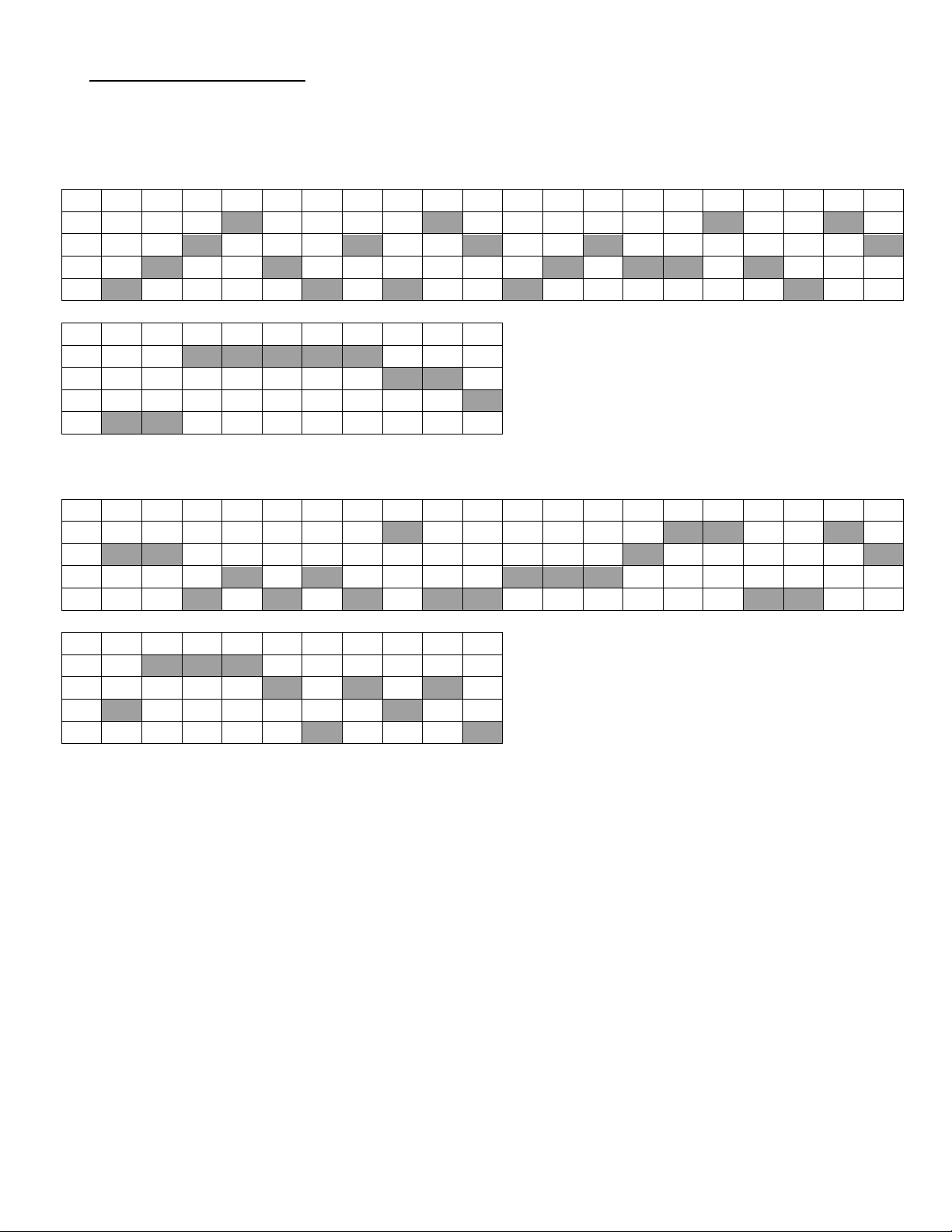
PHIẾU ĐÁP ÁN TRẮC NGHIỆM Mã đề: 132 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 A B C D Mã đề: 209 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 A B C D Mã đề: 357 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 A B C D Mã đề: 485 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 A B C D
II) PHẦN TỰ LUẬN: (4 điểm)
Câu 1: Giải phương trình sau: log x + log x −1 = 2 2 2 ( ) 2 x −4x
Câu 2: Giải bất phương trình sau: 1 < 8 2 Câu 3: Cho hàm số 3 2
y = −x − mx + (4m + 9) x + 5, với m là tham số. Xác định m để hàm số nghịch biến trên tập xác định.
Câu 4: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số ( ) 2 3 e x f x − = trên đoạn [0;2] .
Câu 5: Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a , AD = a 2 ; SA ⊥ ( ABCD) , góc
giữa SC và đáy bằng 60°. Tính thể tích khối chóp S.ABCD theo a .
Câu 6: Cho tam giác ABC vuông tại A , AB = 3a , AC = 4a . Gọi M là trung điểm của AC . Khi quay
quanh AB, các đường gấp khúc AMB , ACB sinh ra các hình nón có diện tích xung quanh lần lượt là S , S . 1 2 Tính tỉ số S1 . S2
Câu 1: Giải phương trình Điều kiện x >1. 0.25 đ sau: 1+ 17 x = log
x + log x −1 = 2 2 2 2 ( ) log x x −1 = 2 2
⇔ x − x − 4 = 0 ⇔ 2 ( ) . 0.25 đ+0.25đ 1− 17 x = (L) 2
Câu 2: Giải bất phương 2 x −4 2 1 x x −4x 3 1 1 − 0.25đ 2 2 x −4x Ta có < 8 ⇔ <
⇔ x − 4x > 3 − trình sau: 1 < 2 2 2 8 2 2
⇔ x − 4x + 3 > 0 ⇔ x <1∨ x > 3 0.25đ Câu 3: Cho hàm số Ta có:TXĐ D=R 3 2
y = −x − mx + (4m + 9) x + 5 2 y′ = 3
− x − 2mx + 4m + 9 . 0.25đ
, với m là tham số. Xác
Hàm số nghịch biến trên ( ;
−∞ +∞) ⇔ y′ ≤ 0,
định m để hàm số nghịch x ∀ ∈( ; −∞ +∞) .
biến trên tập xác định. 3 − < 0 ⇔ 2
⇔ m +12m + 27 ≤ 0 0.25đ ∆′ = (−m)2 −( 3 − ).(4m + 9) ≤ 0 ⇔ m∈[ 9; − − ] 3 . 0.25đ
Câu 4: Tìm giá trị nhỏ nhất Hàm số ( ) 2 3 e x f x − =
xác định và liên tục trên đoạn [0;2] .
và giá trị lớn nhất của hàm f ′(x) 2−3x = − < số ( ) 2 3 e x 3e 0 x ∀ ∈ 0;2 f x − = trên đoạn , [ ]. 0.25đ [0;2]. f ( ) 2 0 = e ; f ( ) 1 2 = . 4 e Do đó 1 m = (GTNN) và 2 M = e (GTLN) 0.25đ 4 e
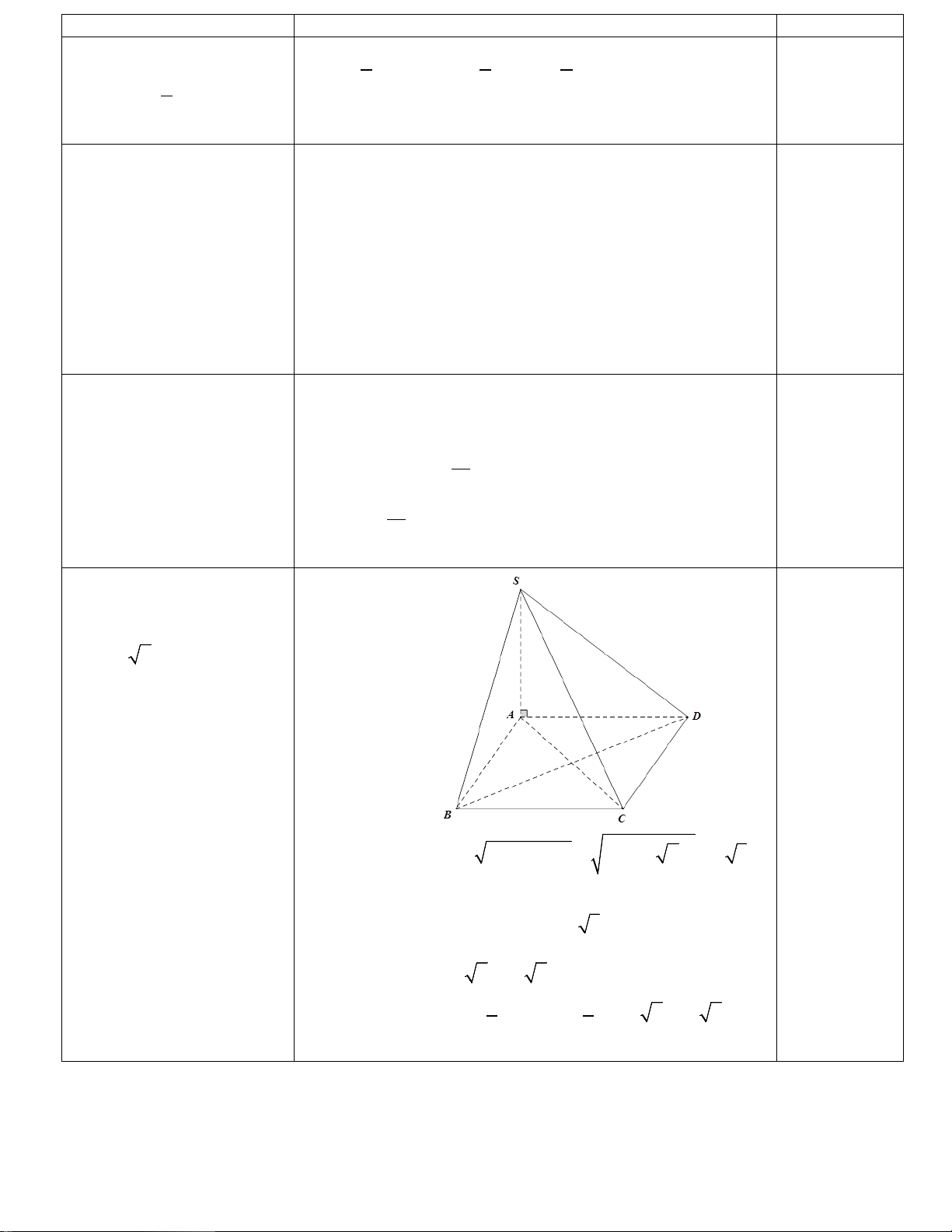
Câu 5: Hình chóp tứ giác
S.ABCD có đáy là hình chữ nhật cạnh AB = a ,
AD = a 2 ; SA ⊥ ( ABCD) ,
góc giữa SC và đáy bằng
60°. Tính thể tích khối chóp
S.ABCD tính theo a .
Ta có AC = AB + BC = a + (a )2 2 2 2 2 = a 3 0.25đ =
SCA (SC,(ABCD)) = 60° Vậy =
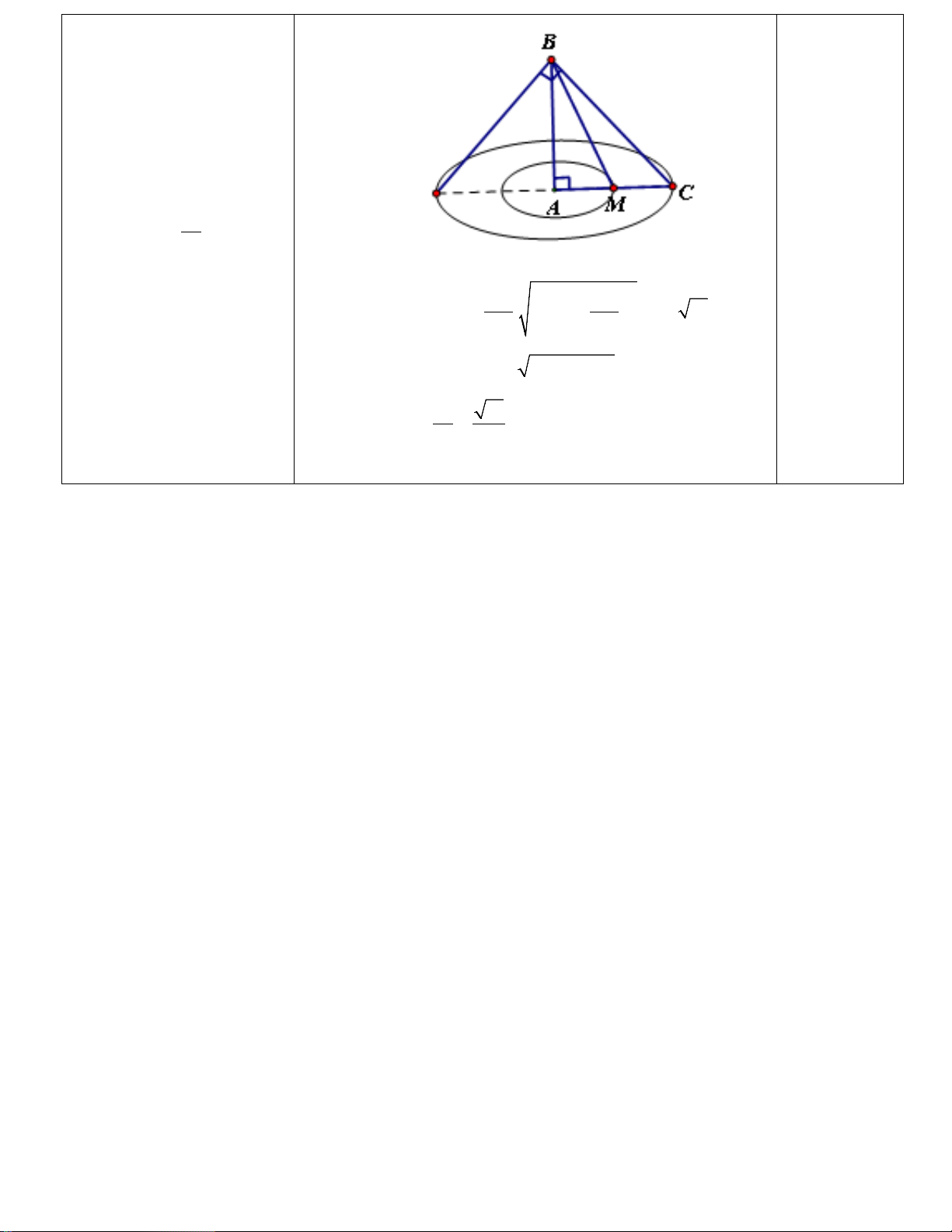
SA AC.tan SCA = a 3.tan 60° = 3a . Ngoài ra 2 S = a a = a ABCD . 2 2 0.25đ Nên 1 1 2 3 V = SA S = a a = a . S ABCD . ABCD .3 . 2 2 . 3 3 0.25đ Câu 6: Cho tam giác ABC vuông tại A ,
AB = 3a , AC = 4a . Gọi M
là trung điểm của AC . Khi
quay quanh AB, các đường
gấp khúc AMB , ACB sinh
ra các hình nón có diện tích
xung quanh lần lượt là S , 1 S
S . Tính tỉ số 1 . 2 S 2 2 AC 2 AC 2 S = π rl = π. . AB + = 2π 13 a ; 1 1 1 2 2 0.25đ 2 2 2
S = π r l = π.AC. AB + AC = 20π a . 0.25đ 2 2 2 Do đó S 13 1 = . S 10 0.25đ 2
Document Outline
- ĐỀ TOAN K12_132 - THPT TÂN PHONG Tp. Hồ Chí Minh
- ĐÁP ÁN TOAN K12 - THPT TÂN PHONG Tp. Hồ Chí Minh




