Đề thi học kì 1 môn Toán 10 năm 2023 - 2024 sách Chân trời sáng tạo đề 5

ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT ………..
Môn: TOÁN 10 SÁCH CTST
Năm học 2023 – 2024
PHẦN I. TRẮC NGHIỆM (7,0 điểm)
Câu 1. Cho tam giác ABC có B =135. Khẳng định nào sau đây là đúng? 1 2 2 A. S = ca . B. S = ab . C. S = bc . D. 2 4 4 2 S = ca . 4
Câu 2. Cho ba điểm phân biệt ,
A B,C . Nếu AB = −3AC thì đẳng thức nào dưới đây đúng? A. BC = 4 − AC , B. BC = 2 − AC ,
C. BC = 2AC , D. BC = 4 AC .
Câu 3. Cho 0º    90º . Mệnh đề nào sau đây là mệnh đề đúng? A. cot (90º  − ) = − tan . B. cos (90º  − ) = sin . C. sin (90º  − ) = −cos . D. tan (90º  − ) = −cot .
Câu 4. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình
2x + y + 5  0  ? x + y +1 0 A. (0;0) . B. (1;0) . C. (0; 2 − ) . D. (0;2).
Câu 5. Trên trục số Ox , gọi A là điểm biểu diễn số 1 và đặt OA = i . Gọi M là
điểm biểu diễn số 4 .
Biểu thị vec tơ OM theo vec tơ i ta được. A M O 1 4 x i 5
A. OM = 3i .
B. OM = 5i . C. OM = i . D. 2
OM = 4i .
Câu 6. Cho ba điểm phân biệt ,
A B,C . Trong các khẳng định sau, khẳng định nào sai?
A. AB + BC = AC .
B. AC + CB = AB .
C. CA + BC = BA .
D. CB + AC = BA .
Câu 7. Cho ba điểm ,
A B,C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. AB = AC . B. k
  0 : AB = k.AC .
C. AC − AB = BC . D.
MA + MB = 3MC, điểm M .
Câu 8. Điểm kiểm tra học kì môn Toán của các bạn Tổ 1, Tổ 2 lớp 10A được cho như sau: Tổ 1 7 8 8 9 8 8 8 Tổ 2 1 0 6 8 9 9 7 8 7 8
Điểm kiểm tra trung bình của 2 tổ là A. 9 . B. 10 . C. 7 . D. 8 .
Câu 9. Lập mệnh đề phủ định của mệnh đề 2 " x
  : x + x + 2022  0" . A. 2 x
  : x + x + 2022  0 . B. 2 x
  : x + x + 2022  0 . C. 2 x
  : x + x + 2022  0 . D. 2 x
  : x + x + 2022  0 .
Câu 10. Trong mặt phẳng tọa độ Oxy, cho các điểm M (4; 3 − ) và N ( 2 − ;0) . Tọa độ
của vectơ MN là. A. (2; 3 − ). B. (6; 3 − ). C. ( 6 − ;3) . D. ( 2 − ;3) .
Câu 11. Cặp số (2;3) là nghiệm của bất phương trình nào sau đây?
A. 2x − 3y −1  0 .
B. x − y  0 .
C. 4x  3y . D.
x − 3y + 7  0 .
Câu 12. Giá trị gần đúng của 5 với độ chính xác 0,002 là A. 2, 237 . B. 2, 236 . C. 2, 24 . D. 2, 23 .
Câu 13. Cho tập hợp A = x  x  
5 . Tập hợp A viết dưới dạng liệt kê các
phần tử là
A. A = 1; 2;3; 4;  5 .
B. A = 0;1; 2;3; 4;  5 .
C. A = 0;1; 2;3;  4 .
D. A = 1; 2;3;  4 .
Câu 14. Cho ba vectơ a , b và c khác vectơ-không. Trong các khẳng định sau,
khẳng định nào sai?
A. a + b = b + a ,
B. (a + b ) + c = a + (b + c ) ,
C. a + 0 = a , D. 0 + a = 0 .
Câu 15. Trong một đợt khảo sát về tốc độ viết của học sinh lớp 3, người ta cho hai
nhóm học sinh chép một đoạn văn trong 15 phút. Bảng dưới đây thống kê số
chữ mỗi bạn viết được.
Số chữ trung bình mỗi học sinh nhóm 1 viết được là: A. 75. B. 74 . C. 73 . D. 72 .
Câu 16. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa
mãn hệ thức MA + MB + 2MC = 0 .
A. M là trung điểm của BC ,
B. M là trung điểm của IC ,
C. M là trung điểm của IA ,
D. M là điểm trên cạnh IC sao cho IM = 2MC .
Câu 17. Cho tam giác ABC vuông tại A có AB = a và 0
B = 60 . Tích vô hướng
của hai vec tơ AC và BC bằng A. 2 a 3 . B. 2 3a . C. 2 −a 3 . D. 2 3 − a .
Câu 18. Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày: 7822201518191311.
khoảng tứ phân vị cho mẫu số liệu là A. 10 . B. 20 . C. 8 . D. 18 .
Câu 19. Cho tam giác ABC đều có cạnh bằng a . Góc của hai vec-tơ A B và BC bằng. A. ( AB BC) 0 , = 30 . B. ( AB BC) 0 ,
= 60 . C. (AB BC) 0 , = 45 . D. (AB BC) 0 , =120 .
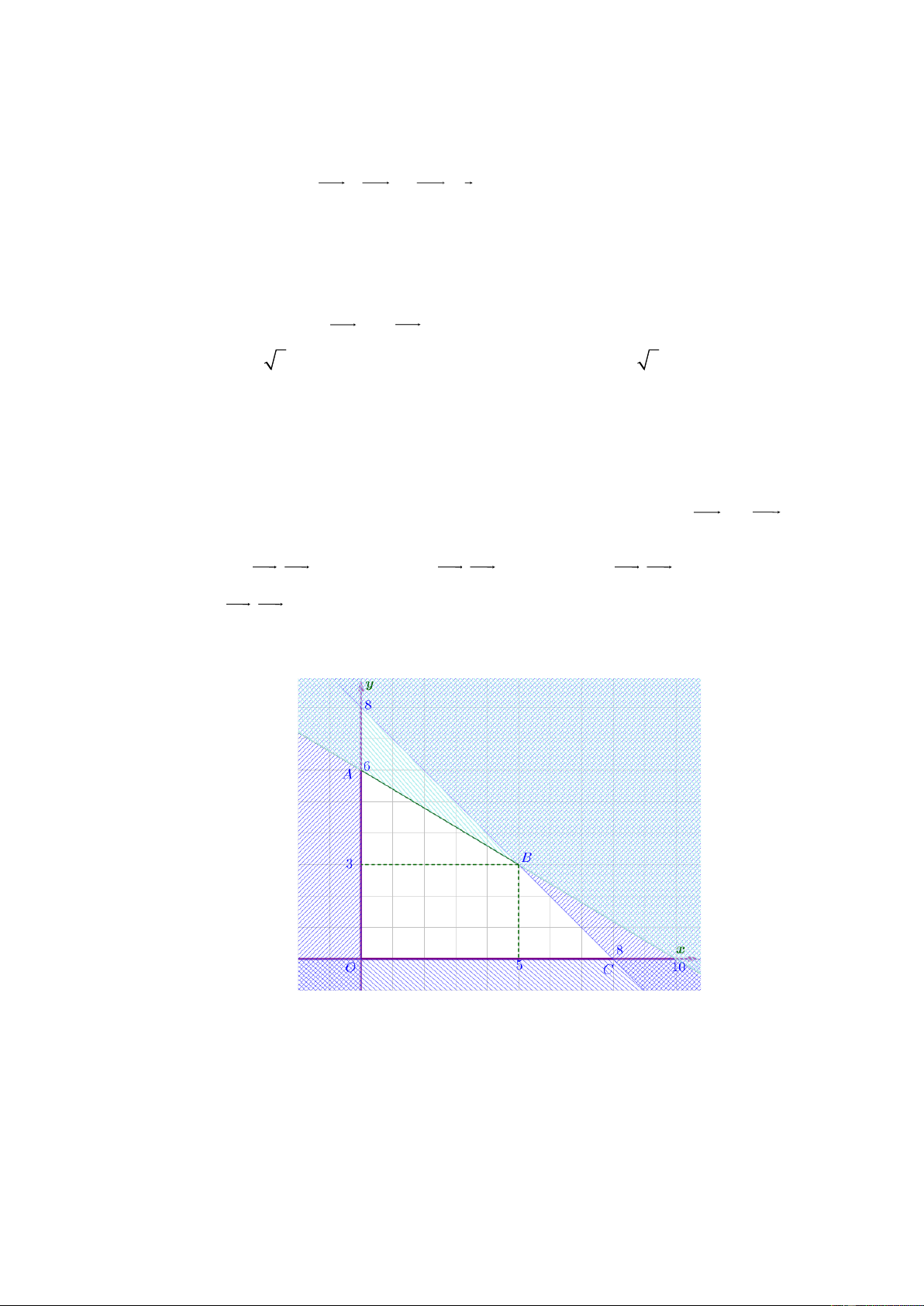
Câu 20. Phần không bị gạch, kể cả các cạnh của tứ giác ABCO là miền nghiệm
của hệ bất phương trình nào sau đây? x + y  8 x + y  8 x + y  8    3
 x + 5y  30 3
 x + 5y  30 3
 x + 5y  30    A. x  0  . B. x  0  . C. x  0  . D. y  0 y  0 y  0 x + y  8 3
 x + 5y  30 x  0  . y  0
Câu 21. Số nhân khẩu trong các hộ gia đình ở một xóm được thống kê ở bảng sau:
Mốt của mẫu số liệu trên là A. 1. B. 4 . C. 2 . D. 5 .
Câu 22. Cho lục giác đều ABCDEF có tâm O . Trong các khẳng định sau, khẳng định nào sai?
A. OA + OB + OC + OD + OE + OF = 0 ,
B. OA + AB + BO = 0 ,
C. OA + ED + FA = 0 ,
D. OA + FE = 0 .
Câu 23. Số quy tròn của số gần đúng 5, 4857216  0,001 là A. 5, 486 . B. 5, 48 . C. 5, 49 . D. 5, 485 .
Câu 24. Cho tam giác ABC có
= 4, = 45o, = 75o AB A C . Tính độ dài cạnh
BC của tam giác ABC . A. 4 3 . B. 4 3 − 4 . C. 4 3 − 8 . D. 4 3 + 4 .
Câu 25. Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu: 9 8 15 8 20
Số trung vị của mẫu số liệu trên là A. 8 . B. 15 . C. 20 . D. 9 .
Câu 26. Trong một cuộc điều tra dân số, người ta viết dân số của một thành phố là
8053663 người  10000 người. Sai số tương đối của số liệu điều tra trên là A.   0,12% . B.  = 0,12% . C.   1, 2% . D. a a a  =1,2%. a
Câu 27. Điều kiện của a và b sao cho (a −b)2 = 0 là
A. a và b đối nhau.
B. a và b ngược hướng.
C. a và b bằng nhau.
D. a và b cùng hướng.
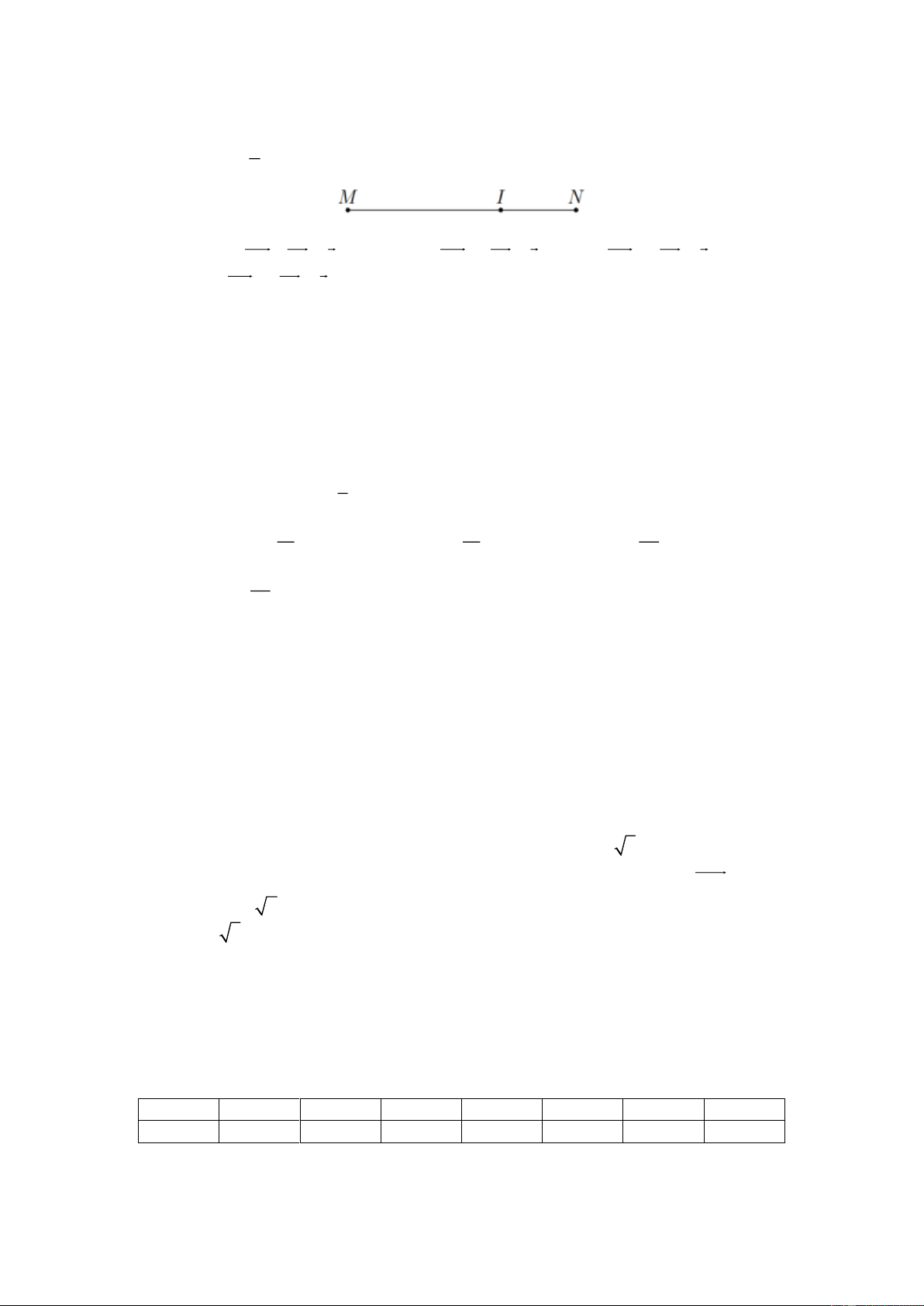
Câu 28. Cho hai điểm phân biệt M và N , gọi I là điểm thuộc đoạn thẳng MN 2 sao cho MI = MN . 3
Mệnh đề nào dưới đây đúng?
A. IM + IN = 0 .
B. 2IM + 3IN = 0 .
C. IM + 2IN = 0 . D. 3IM + 2IN = 0 .
Câu 29. Hàm lượng Natri (đơn vị mg) trong 100 g một số loại ngũ cốc được cho như sau: 0 340 70 140 200 180 210 150 100 130 140 180 190 160 290 50 220 180 200 210.
Tìm giá trị bất thường trong mẫu số liệu trên là A. 310; 340 . B. 0; 310 . C. 0; 340 . D. 300; 310 . 1
Câu 30. Cho sin = . Tính giá trị của 2 2
P = 3sin  + cos  . 3 11 9 25 A. P = . B. P = . C. P = . D. 9 11 9 9 P = . 25
Câu 31. Trong mặt phẳng tọa độ Oxy, cho các điểm A(2;7) và B( 5 − ;2). Tọa độ
điểm C để tứ giác OACB là hình bình hành là. A. ( 3 − ;9) . B. (7;5) . C. (3; 9 − ) . D. ( 7 − ; 5 − ).
Câu 32. Cho tam giác ABC có điểm A(1; 2
− ), B(5;2),C (8; 2
− ) . Số đo góc A của tam giác ABC là A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Câu 33. Trong mặt phẳng tọa độ Oxy, gọi E ( 2
− ;0) , F (0;2 3) lần lượt là hình
chiếu của điểm M lên các trục tọa độ Ox, Oy. Độ dài của vectơ OM là. A. 2 2 . B. 4 . C. 2 . D. 3 .
Câu 34. Số ca nhiễm mới Covid 19 trong một tuần của một thành phố như sau
7122 7310 7308 5549 7539 5629 6158
Số ca nhiễm mới trung bình trong một tuần của thành phố đó khoảng A. 7308 . B. 6660 . C. 6659 . D. 6158 .
Câu 35. Điểm kiểm tra học kì môn Toán của các bạn Tổ 1, Tổ 2 lớp 10A được cho như sau: Tổ 1 7 8 8 9 8 8 8 Tổ 2 10 6 8 9 9 7 8
Gọi R , R lần lượt là các khoảng biến thiên của tổ 1 và tổ 2. R − R bằng 1 2 1 2 A. 2 − . B. 6 . C. 2 . D. 6 − .
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. Trong mặt phẳng tọa độ Oxy cho A(5;2) , B(2;5) . Tìm tọa độ điểm M nằm trên
đoạn thẳng AB sao cho MA = 2MB .
Bài 2. Cho hình chữ nhật ABCD có cạnh AB = 4, BC = 6 , M là trung điểm của
BC , N là điểm trên cạnh CD sao cho ND = 3NC . Tính bán kính đường
tròn ngoại tiếp tam giác AMN .
Bài 3. Điểm số của hai vận động viên bắn cung trong 10 lần bắn thử để chuẩn bị cho
Olympic Tokyo 2020 được ghi lại như sau: Vận động viên A 10 9 8 10 9 9 9 10 9 8 Vận động viên B 7 10 10 10 10 7 8 10 10 10
Tìm khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mỗi dãy số liệu
trên. Từ đó hãy cho biết vận động viên nào có thành tích bắn thử ổn định hơn?
Bài 4. Hai người cùng kéo một con thuyền với hai lực F = O ,
A F = OB có độ lớn lần 1 2
lượt là 400 N, 600 N (hình vẽ). Cho biết góc giữa hai véc-tơ là 60 . Tìm độ
lớn của véc-tơ hợp lực F là tổng của hai lực F và F . 1 2
------------------ Hết ------------------ BẢNG ĐÁP ÁN 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
D D B C D D B C D C B C B D A B B A D C B C C B D 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5
6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 A C C C A A C B C A