Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường Diên Hồng – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THCS&THPT Diên Hồng, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HỒ CHÍ MINH
TRƯỜNG THCS-THPT DIÊN HỒNG
KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
MÔN TOÁN – LỚP 10
Th
ời gian l
àm bài: 90
phút (không k
Câu 1. (0.5 điểm) Tìm tập xác định của hàm số:
3
1 2
x
y
x x
.
Câu 2. (1.0 điểm) Xác định Parabol
2
( ) :
P y ax bx c
có đồ thị hàm số như hình vẽ sau:
y
3
x
0
1
2
3
4
-1
Câu 3. (3.0 điểm) Giải các phương trình và hệ phương trình sau:
a)
2
3 10 44 8
x x x
. b)
2 2
3 2 3 4
x x x x
.
c)
2 2
13
2
x xy y
x y
.
Câu 4. (1.0 điểm) Cho phương trình
2
2 2 1 0
m x m x m
. Tìm
m
để phương trình có 2
nghiệm phân biệt
1 2
,
x x
thỏa mãn
2 2
1 2 1 2
5 2
x x x x
.
Câu 5. (1.0 điểm) Tìm tất cả các giá trị thực của tham số m để phương trình:
2 2
5 6 2
m m x m m
vô nghiệm.
Câu 6. (0.5 điểm) Tìm giá trị nhỏ nhất của hàm số:
2
2 1
y x
x
với
1
2
x
.
Câu 7. (2.5 điểm) Trong mặt phẳng Oxy, cho 3 điểm
2;5 , 3; 2 , 5; 1
A B C
.
a) Chứng minh
, ,
A B C
là ba đỉnh của một tam giác. Tìm tọa độ trọng tâm của tam giác
ABC
.
b) Tìm tọa độ trực tâm H của tam giác
ABC
.
Câu 8. (0.5điểm) Cho hình chữ nhật
ABCD
có
, 2
AB a AD a
. Gọi
K
là trung điểm của
AD
.
Chứng minh
BK AC
 
.
----------- HẾT -----------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh:……………..…………………………Số báo danh:………………………………
ĐỀ CHÍNH THỨC
Đề có 01 trang
SỞ GD&ĐT TP. HỒ CHÍ MINH KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
TRƯỜNG THCS - THPT DIÊN HỒNG MÔN TOÁN – LỚP 10
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM
CÂU NỘI DUNG TRẢ LỜI ĐIỂM
Câu 1
(0.5
đi
ể
m)
Hàm số xác định khi và chỉ khi:
3 0
1 0
2 0
x
x
x
3
1
2
x
x
x
. Vậy TXĐ:
( ;3] \ 2;1
D

.
0,25
0,25
Câu 2 (1 điểm)
(P) có đỉnh
2; 1
I
đi qua điểm
4;3
A
4 2 1
4 0
16 4 3
a b c
a b
a b c
1
4
3
a
b
c
. Vậy
2
: y 4 3
P x x
0,5
0,5
Câu 3 (3 điểm)
a
2
2
2
8 0
3 10 44 8
3 10 44 8
x
x x x
x x x
2
8
8
6( )
2 6 108 0
9( )
x
x
x n
x x
x n
.
Vậy phương trình có tập nghiệm
9;6
S
.
0,25
0,5
0,25
b
2 2
3 2 3 4
x x x x
Đặt
2
3 2 0
t x x t
. Khi đó,
2 2
3 2
x x t
.
Phương trình đã cho trở thành:
2 2
3( )
2 4 6 0
2( )
t n
t t t t
t l
.
Với
3
t
ta có:
2
2
3 0
3 2 3
3 2 9
x x
x x
0,25
0,25
0,25
3 37
2
3 37
2
x
x
. Vậy tập nghiệm
3 37
2
S
0,25
c
2 2
2
2
2
2
13
2
2 2 13
2
2
1
3 6 9 0
3
1; 3
3; 1
x y
x xy y
x y
y y y y
x y
x y
y
y y
y
y x
y x
Vậy hệ phương trình có 2 nghiệm:
3;1 , 1; 3
.
0,25
0,5
0,25
Câu 4 (1 điểm)
Câu 5. (1 điểm)
2
2 1 4 2 4 1.
m m m m
Phương trình có 2 nghiệm phân biệt
0
0
a
2
2 0
1
4 1 0
4
m
m
m
m
.
2
2 2
1 2 1 2 1 2 1 2
5 2 3 2
x x x x x x x x
2
(2 1) 3
2 0
2 2
m m
m m
2 2
4 4 1 3 ( 2) 2( 2) 0
m m m m m
2
1( )
5 2 7 0
7
( )
5
m l
m m
m n
. Vậy
7
5
m
.
Tìm tất cả các giá trị thực của tham số m để phương trình:
2 2
5 6 2
m m x m m
vô nghiệm.
PT đã cho vô nghiệm khi:
2
2
2
3
5 6 0
3
0
2 0
2
m
m
m m
m
m
m m
m
0,25
0,25
0,25
0,25
Câu 6 (1.0 điểm)
Với
1
2
x
ta có:
1
0
2
x
. Khi đó:
2 1 1 1
1
2 1 2 2
2
y x x
x
x
1 1 1 1 5
2 . 2
1
2 2 2 2
2
x
x
Vậy với
1
2
x
hàm số đã cho có GTNN là
5
2
.
0,25
0,25
Câu 7 (2.5 điểm)
a
5; 7 , 3; 6
AB AC

.
Ta có:
5 7
3 6
.
Do đó
,
AB AC
 
không cùng phương => A, B, C không
thẳng hàng => A, B ,C là ba đỉnh của một tam giác.
Gọi G là trọng tâm của tam giác ABC, ta có:
2 3 5 4
3 3 3
5 2 1 2
3 3 3
A B C
G
A B C
G
x x x
x
y y y
y
. Vậy
4 2
;
3 3
G
.
0,25
0,25
0,25
0,25
b
2; 5
8;1
H H
AH x y
BC


3; 2
3; 6
H H
BH x y
AC


Vì H là trực tâm của tam giác ABC nên ta có:
. 0
. 0
AH BC AH BC
BH AC BH AC
  
   
8 2 5 0
8 21
3 6 3
3 3 6 2 0
H H
H H
H H
H H
x y
x y
x y
x y
43
16
1
2
H
H
x
y
. Vậy
43 1
;
16 2
H
.
0,5
0,25
0,5
0,25
HẾT
Câu 8 (0.5điểm)
. .
. . . .
BK AC BA AK AD DC
BA AD BA DC AK AD AK DC
 
 
2 2
1
0 0
2
BA AD
(Vì
,
BA AD AK DC

)
2 2
0
Suy ra .
a a
BK AC
 
0,25
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HỒ CHÍ MINH KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
TRƯỜNG THCS-THPT DIÊN HỒNG MÔN TOÁN – LỚP 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC Đề có 01 trang 3  x
Câu 1. (0.5 điểm) Tìm tập xác định của hàm số: y   . x   1 x  2
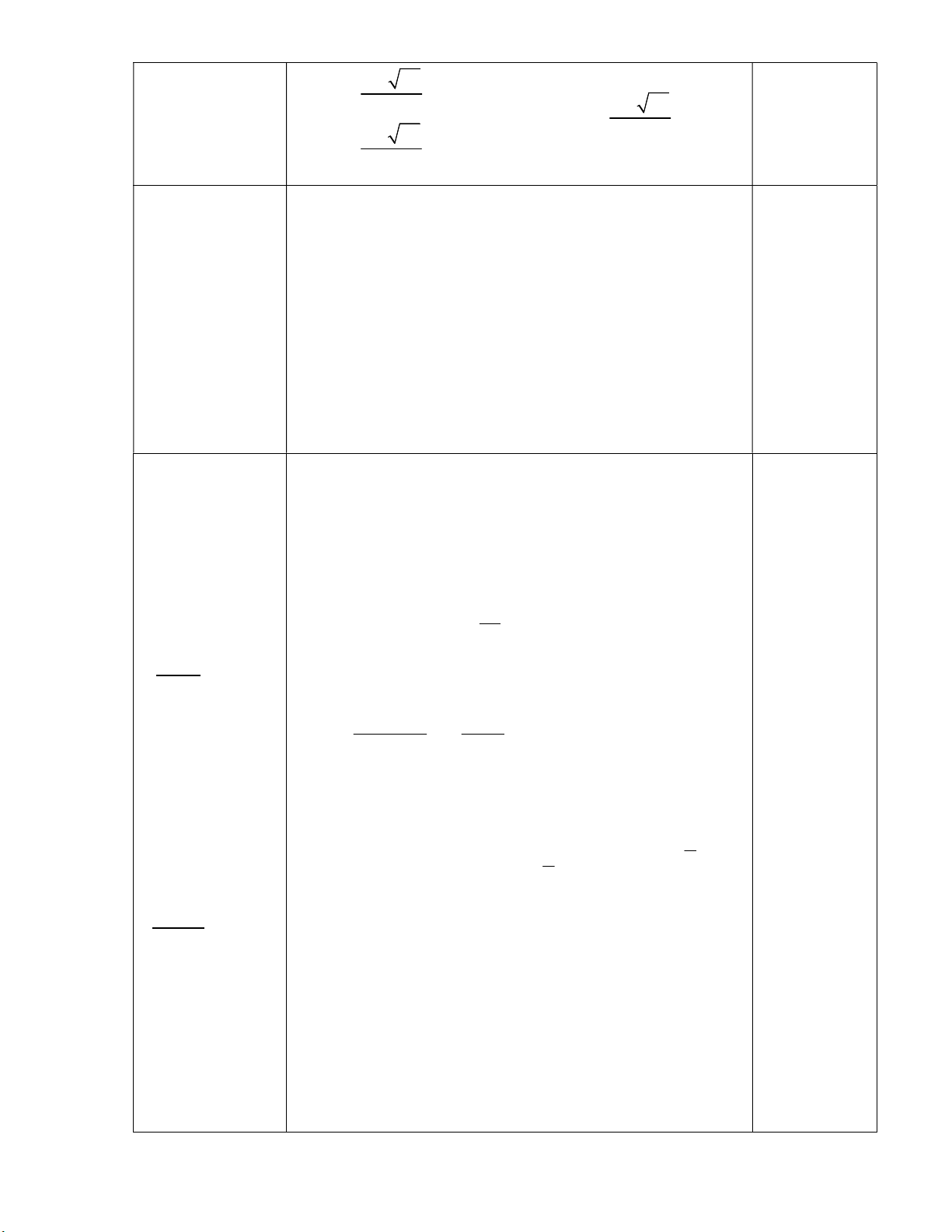
Câu 2. (1.0 điểm) Xác định Parabol 2
(P) : y  ax  bx  c có đồ thị hàm số như hình vẽ sau: y 3 x 0 1 2 3 4 -1
Câu 3. (3.0 điểm) Giải các phương trình và hệ phương trình sau: a) 2
3x 10x  44  8  x . b) 2 2
x  3x  2  x  3x  4 . 2 2 x  xy  y 13 c)  . x  y  2 
Câu 4. (1.0 điểm) Cho phương trình m   2 2 x  2m  
1 x  m  0 . Tìm m để phương trình có 2
nghiệm phân biệt x , x thỏa mãn 2 2 x  x  5x x  2 . 1 2 1 2 1 2
Câu 5. (1.0 điểm) Tìm tất cả các giá trị thực của tham số m để phương trình:  2 m  m   2 5
6 x  m  2m vô nghiệm. 2 1
Câu 6. (0.5 điểm) Tìm giá trị nhỏ nhất của hàm số: y  x  với x  . 2x 1 2
Câu 7. (2.5 điểm) Trong mặt phẳng Oxy, cho 3 điểm A2;5, B 3  ;2,C 5;  1 . a) Chứng minh ,
A B,C là ba đỉnh của một tam giác. Tìm tọa độ trọng tâm của tam giác ABC .
b) Tìm tọa độ trực tâm H của tam giác ABC .
Câu 8. (0.5điểm) Cho hình chữ nhật ABCD có AB  a, AD  a 2 . Gọi K là trung điểm của AD .   Chứng minh BK  AC .
-----------  HẾT  -----------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh:……………..…………………………Số báo danh:………………………………
SỞ GD&ĐT TP. HỒ CHÍ MINH KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
TRƯỜNG THCS - THPT DIÊN HỒNG MÔN TOÁN – LỚP 10
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM CÂU NỘI DUNG TRẢ LỜI ĐIỂM Câu 1 (0.5 điểm) 3   x  0 
Hàm số xác định khi và chỉ khi: x 1  0  0,25 x  2  0  x  3 
 x  1 . Vậy TXĐ: D  ( ;  3] \ 2  ;  1 . 0,25 x  2  (P) có đỉnh I 2;  1 đi qua điểm A4;3 4a  2b  c  1   0,5 4a  b  0 Câu 2 (1 điểm) 1  6a  4b  c  3  a  1 0,5   b   4 . Vậy P 2 : y  x  4x  3 c  3  Câu 3 (3 điểm) 8   x  0  2
3x 10x  44  8  x   0,25 3  x 10x  44   8 x2 2   a x 8 x  8     x  6(n) . 0,5 2 2x  6x 108  0  x  9(n)
Vậy phương trình có tập nghiệm S   9  ;  6 . 0,25 2 2
x  3x  2  x  3x  4 Đặt 2
t  x  3x  2 t  0. Khi đó, 2 2 x  3x  t  2 . 0,25
Phương trình đã cho trở thành: t  3(n) b 2 2
t  t  2  4  t  t  6  0   . 0,25 t  2  (l) 3   0 Với t  3 ta có: 2 x  3x  2  3   2 x  3x  2  9 0,25  3  37 0,25 x   2     3 37  
. Vậy tập nghiệm S     3  37  2   x   2 2 2     x  2 13   y x xy y     x  y  2    2  y  2  2   y 2 y  y  13 0,25 x  2  y x  2   y     y 1 2 3  y  6y  9  0  c  y  3   y  1; x  3    0,5  y  3; x  1
Vậy hệ phương trình có 2 nghiệm: 3;  1 ,1;3 . 0,25    m  2 2
1  4mm  2  4m 1. a  0
 Phương trình có 2 nghiệm phân biệt   0,25   0 m  2 m  2  0      1  . 0,25 4m 1  0 m   4 Câu 4 (1 điểm)
 x  x  5x x  2  x  x  3x x  2 1 2 1 2  1 22 2 2 1 2 2 0,25 (2m 1)  3m    2  0  m 2    m  2 2 2
 4m  4m 1 3m(m  2)  2(m  2)  0 m  1(l) 7 0,25 2 5m 2m 7 0       7 . Vậy m  .   5 m (n)  5 Câu 5. (1 điểm)
Tìm tất cả các giá trị thực của tham số m để phương trình:  2 m  m   2 5
6 x  m  2m vô nghiệm. PT đã cho vô nghiệm khi: m  2  2  m  5m  6  0 m  3      m  3 2 m  2m  0 m  0  m  2 1 1
Với x  ta có: x   0 . Khi đó: 2 2 2  1  1 1 y  x   x      2x 1  2 1  2 0,25 x  2 Câu 6 (1.0 điểm)  1  1 1 1 5  2 x  .   2      2 1  2 2 2 x  2 1 5
Vậy với x  hàm số đã cho có GTNN là . 0,25 2 2 Câu 7 (2.5 điểm)    AB  5; 7
 , AC  3;6 . 0,25 5 7 Ta có:  . 0,25 3 6  
Do đó AB, AC không cùng phương => A, B, C không 0,25 a
thẳng hàng => A, B ,C là ba đỉnh của một tam giác.
 Gọi G là trọng tâm của tam giác ABC, ta có:  x  x  x 2  3  5 4 A B C x     G  3 3 3  4 2   . Vậy G ; 0,25   . y  y  y 5  2 1 2   3 3  A B C y    G  3 3 3   AH   x  2; y  5 BH   x  3; y  2 H H  H H    BC  8;  1 AC  3;6 0,5
Vì H là trực tâm của tam giác ABC nên ta có:     AH  BC AH.BC  0 0,25
     BH  AC BH.AC  0 b 8    x  2  y      H  5 0 H 8x y 21 H H     0,5 3
 x  3  y   x  y  H  6 2 H  0 3 6 3  H H  43 x   H  16    43 1  . Vậy H ;   . 0,25 1    16 2  y  H  2
     
BK.AC  BA  AK . AD  DC
         B . A AD  B . A DC  AK.AD  AK.DC 0,25  
     0   2 BA  1 2
 AD  0 (Vì BA  AD, AK  DC ) Câu 8 (0.5điểm) 2 2 2  a  a  0   0,25 Suy ra BK  AC. HẾT