Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường Lý Thái Tổ – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Lý Thái Tổ, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Bài 1 (1.0 điểm). Tìm tập xác định của các hàm số:
a)
2
4 1
5
x
y
x x
b)
4 4
y x x
Bài 2 (1.5 điểm). Giải các phương trình sau:
a)
2 2
2 3 1 7 6
x x x x
b)
2
x x x
Bài 3 (2.0 điểm).
a) Xét sự biến thiên và vẽ đồ thị của hàm số:
2
2 4 2
y x x
b) Xác định
a
,
b
để Parabol
2
( ) : 2
P y ax bx
qua
1;0
A
và có trục đối xứng
3
2
x
.
Bài 4 (1.5 điểm). Tìm
m
để phương trình:
2 2
2 2 2 0
x m x m
có hai nghiệm
1 2
,
x x
thỏa điều kiện
2 2
1 2 1 2
46
x x x x
.
Bài 5 (1.0 điểm). Giải phương trình:
√
x
−2x+9+
√
x
−2x+4 = 5
Bài 6 (3.0 điểm). Trong mặt phẳng tọa độ cho 3 điểm
1; 3
A
,
2;1
B ,
6;7
C .
a) Chứng minh rằng tam giác
ABC
vuông. Tính diện tích và chu vi tam giác
ABC
.
b) Tìm tọa độ trọng tâm, tâm đường tròn ngoại tiếp tam giác
ABC
.
c) Tính
cos ;
AB OC
với
O
là gốc tọa độ.
------------------HẾT-----------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
TRƯỜNG THPT LÝ THÁI TỔ MÔN : TOÁN – KHỐI 10
THỜI GIAN: 90 PHÚT
(Không kể thời gian phát đề)
ĐÁP ÁN MÔN TOÁN - KHỐI 10
HỌC KỲ 1, NĂM HỌC 2019-2020
II. PHẦN TỰ LUẬN
BÀI NỘI DUNG ĐIỂM
1
Bài 1 (1.0 điểm). Tìm tập xác định của các hàm số:
a)
2
4 1
5
x
y
x x
b)
4 4
y x x
1.0
a) ĐKXĐ:
2
4 0
5 0
x
x x
0.25
4
0; 5
x
x x
Vậy TXĐ của hàm số là:
4; \ 0;5
D 
0.25
b) ĐKXĐ:
4 0
4 0
x
x
0.25
4
4
x
x
Vậy TXĐ của hàm số là:
4;4
D
0.25
2
Bài 2 (1.5 điểm). Giải các phương trình sau:
a)
2 2
2 3 1 7 6
x x x x
b)
2
x x x
1.0
a)
2 2
2 2
2 2
2 3 1 7 6
2 3 1 7 6
2 3 1 7 6
x x x x
x x x x
x x x x
0.5
2
2
1; 5
4 5 0
7
1;
3 10 7 0
3
x x
x x
x x
x x
Vậy tập nghiệm của pt đã cho là:
7
1; 5;
3
S
0.25
b)
2
2
2
2 0
5 21 8 2
5 21 8 2
x
x x x
x x x
0.25
2
2
4 17 4 0
x
x x
2
4
1
4;
4
x
x
x x
Vậy tập nghiệm của pt đã cho là:
4
S
0.5
3
Bài 3 (2.0 điểm).
a) Xét sự biến thiên và vẽ đồ thị của hàm số:
2
2 4 2
y x x
2.0
b) Xác định
a
,
b
để Parabol
2
( ) : 2
P y ax bx
qua
1;0
A
và có
trục đối xứng
3
2
x
.
3
a) Xét sự biến thiên và vẽ đồ thị của hàm số:
2
2 4 2
y x x
*) TXĐ:
D
0.25
*) Sự biến thiên:
2 0; 1
2
b
a
a
Vậy: Hàm số nghịch biến trên khoảng
;1

Hàm số đồng biến trên khoảng
1;

Bảng biến thiên:
0.25
*) Đồ thị:
Đỉnh
1;0
I
; Trục đối xứng
1
x
Bảng giá trị tương ứng:
0.25
Vẽ đồ thị:
0.25
b) b) Xác định
a
,
b
để Parabol
2
( ) : 2
P y ax bx
qua
1;0
A
và có trục
đối xứng
3
2
x
.
Parabol
( )
P
qua
1;0 2 0 2 1
A a b a b
0.25
Parabol
( )
P
có trục đối xứng
3 3
3 0 2
2 2 2
b
x a b
a
.
0.25
Từ (1) và (2), ta có:
2 1
3 0 3
a b a
a b b
0.5
4
Bài 4 (1.5 điểm). Tìm
m
để phương trình:
2 2
2 2 2 0
x m x m
có hai
nghiệm
1 2
,
x x
thỏa điều kiện
2 2
1 2 1 2
46
x x x x
.
1.5
Ta có:
2
' 2
2 2 4 2
m m m
Để PT đã cho có hai nghiệm
1 2
,
x x
thì:
'
1
0 4 2 0 1
2
m m
.
0.5
Theo Định lý Vi-ét, ta có:
1 2
2
1 2
2 2
2
x x m
x x m
0.25
Mà:
2
2 2
1 2 1 2 1 2 1 2
46 3 46
x x x x x x x x
2
2 2
2 2 3 2 46 16 36 0
m m m m
2
18
m
m
0.5
Kết hợp với (1), ta có:
2
m
0.25
5
Bài 5 (1.0 điểm). Giải phương trình:
√
x
−
2x
+
9
+
√
x
−
2x
+
4
=
5
1.0
Đặt t =
√
x
−
2x
+
4
(t ≥
√
3
)
Phương trình trở thành:
√
t
+5+t = 5
5
−
t
≥
0
t
+
5
=
(
5
−
t
)
󰇥
t ≤ 5
t
=
2
Với t = 2 => x = 0 hay x = 2
0.75
0.25
6
Bài 6 (3.0 điểm). Trong mặt phẳng tọa độ cho 3 điểm
1; 3
A
,
2;1
B ,
6;7
C .
3.0
a) Chứng minh rằng tam giác
ABC
vuông. Tính diện tích và chu vi tam
giác
ABC
.
1.0
Ta có:
2 2
3;4 3 4 25 5
AB AB

2
2
5;10 5 10 125 5 5
AC AC

2
2
8;6 8 6 100 10
BC BC

Vậy:
2 2 2
25 100 125
AB BC AC
; Hay tam giác
ABC
vuông tại
B
0.5
*) Tính diện tích tam giác:
1 1
. .5.10 25
2 2
ABC
S AB BC
.
*) Tính diện tích và chu vi tam giác:
0.5
2 5 5 5 10 5(3 5)
p AB AC BC
.
b) Tìm tọa độ trọng tâm, tâm đường tròn ngoại tiếp tam giác
ABC
.
1.0
*) Tìm tọa độ trọng tâm
G
của tam giác
ABC
là:
1 2 6 5
5 5
3 3 3
;
3 1 7 5
3 3
3 3 3
A B C
G
A B C
G
x x x
x
G
y y y
y
*) Tìm tâm
I
của
đường tròn ngoại tiếp tam giác
ABC
:
Do tam giác
ABC
vuông tại
B
nên
I
là trung điểm của
AC
:
1 6 7
7
2 2 2
;2
3 7 2
2
2 2
A C
I
A C
I
x x
x
I
y y
y
.
0.5
c) Tính
cos ;
AB OC
với
O
là gốc tọa độ.
1.0
3;4 ; 6;7
AB OC
0.5
2
2
3. 6 4.7
. 10 2 85
cos ;
85
5 85
.
5. 6 7
AB OC
AB OC
AB OC
0.5
(Mọi cách làm đúng khác đều đạt điểm tối đa)
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
TRƯỜNG THPT LÝ THÁI TỔ MÔN : TOÁN – KHỐI 10 THỜI GIAN: 90 PHÚT
(Không kể thời gian phát đề)
Bài 1 (1.0 điểm). Tìm tập xác định của các hàm số: a) x  4 1 y  b) y  4  x  x  4 2 5x  x
Bài 2 (1.5 điểm). Giải các phương trình sau: a) 2 2
2x  3x 1  x  7x  6 b) 2 5x  21x  8  x  2 Bài 3 (2.0 điểm).
a) Xét sự biến thiên và vẽ đồ thị của hàm số: 2 y  2x  4x  2
b) Xác định a ,b để Parabol 2
(P) : y  ax  bx  2 qua A1;0 và có trục đối xứng 3 x  . 2
Bài 4 (1.5 điểm). Tìm m để phương trình: 2 x  m   2 2
2 x  m  2  0 có hai nghiệm x , x 1 2 thỏa điều kiện 2 2 x  x  x x  46 1 2 1 2 .
Bài 5 (1.0 điểm). Giải phương trình: √x − 2x + 9 + √x − 2x + 4 = 5
Bài 6 (3.0 điểm). Trong mặt phẳng tọa độ cho 3 điểm A1;3 , B2;  1 , C 6;7 .
a) Chứng minh rằng tam giác ABC vuông. Tính diện tích và chu vi tam giác ABC .
b) Tìm tọa độ trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC .   c) Tính cos A ;
B OC  với O là gốc tọa độ.
------------------HẾT-----------------
ĐÁP ÁN MÔN TOÁN - KHỐI 10
HỌC KỲ 1, NĂM HỌC 2019-2020 II. PHẦN TỰ LUẬN BÀI NỘI DUNG ĐIỂM
Bài 1 (1.0 điểm). Tìm tập xác định của các hàm số:   a) x 4 1 y  b) y  4  x  x  4 1.0 2 5x  x  x  4  0 a) ĐKXĐ:  0.25 2 5x  x  0 x  4  1   x  0; x  5 0.25
Vậy TXĐ của hàm số là: D  4; \0;  5 4  x  0 b) ĐKXĐ:  0.25 4  x  0  x  4   x  4 0.25
Vậy TXĐ của hàm số là: D  4;4
Bài 2 (1.5 điểm). Giải các phương trình sau: a) 2 2
2x  3x 1  x  7x  6 b) 2 5x  21x  8  x  2 1.0 2 2
 2x  3x 1  x  7x  6 a) 2 2
2x  3x 1  x  7x  6   2 2x  3x 1     2x 7x6 0.5 x  1; x  5 2  x  4x  5  0     7 2 3x 10x  7  0  x 1; x   3 0.25 2
Vậy tập nghiệm của pt đã cho là:  7  S  1  ;5;   3   x  2  0 b)  2
5x  21x  8  x  2  5 0.25  x  21x  8   x  22 2    x 2 x  2      1  x  4 2  4x 17x  4  0 x  4; x    4 0.5
Vậy tập nghiệm của pt đã cho là: S    4 Bài 3 (2.0 điểm). 3
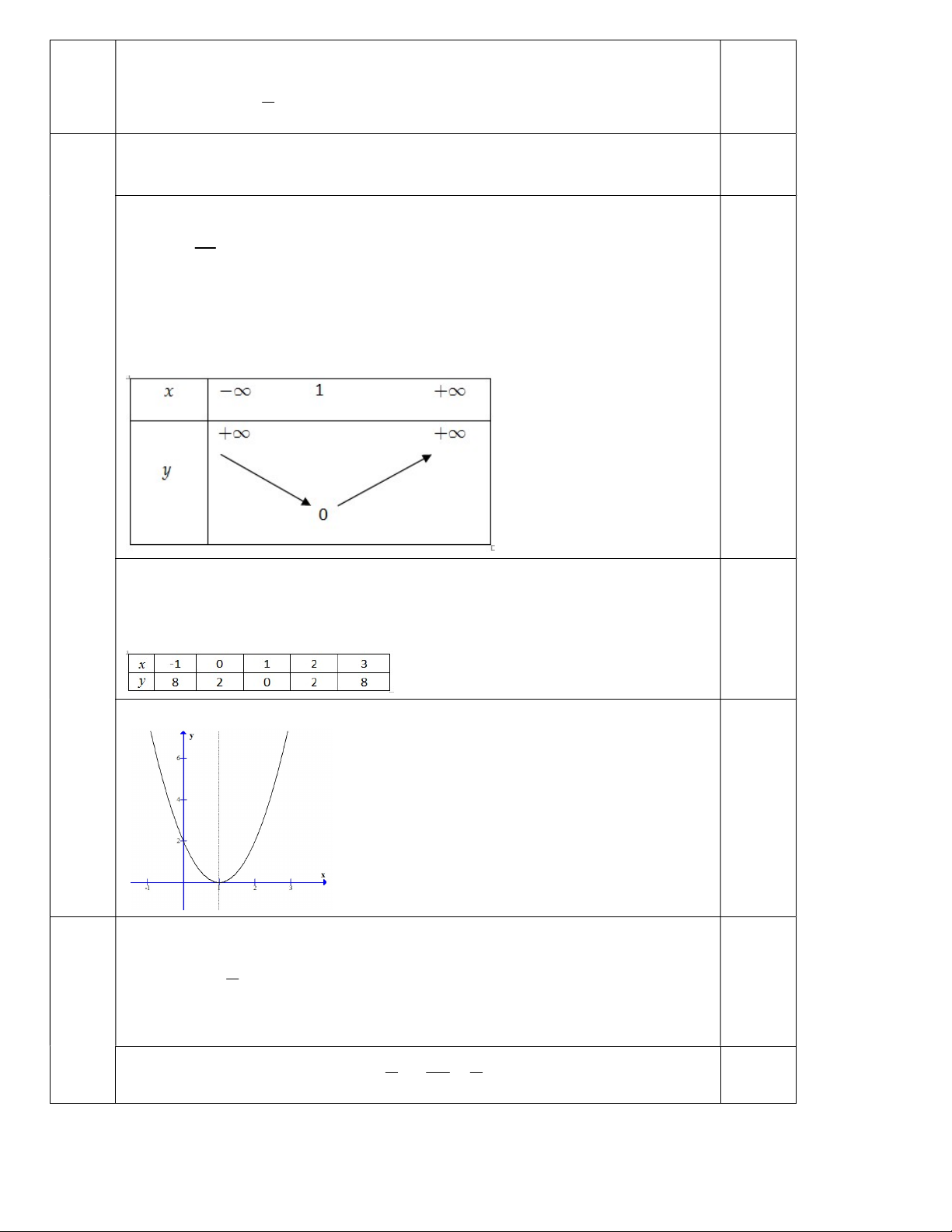
a) Xét sự biến thiên và vẽ đồ thị của hàm số: 2 2.0 y  2x  4x  2
b) Xác định a ,b để Parabol 2
(P) : y  ax  bx  2 qua A1;0 và có 3 trục đối xứng x  . 2
a) Xét sự biến thiên và vẽ đồ thị của hàm số: 2 y  2x  4x  2 0.25 *) TXĐ: D   *) Sự biến thiên: b  a  2  0; 1 2a
Vậy: Hàm số nghịch biến trên khoảng ;  1
Hàm số đồng biến trên khoảng 1; Bảng biến thiên: 0.25 3 *) Đồ thị:
Đỉnh I 1;0 ; Trục đối xứng x  1
Bảng giá trị tương ứng: 0.25 Vẽ đồ thị: 0.25
b) b) Xác định a ,b để Parabol 2
(P) : y  ax  bx  2 qua A1;0 và có trục 3 đối xứng x  . 2 0.25
Parabol (P) qua A1;0  a  b  2  0  a  b  2    1 3 b 3
Parabol (P) có trục đối xứng x  
  3a  b  0 2. 2 2a 2 0.25 a  b  2 a  1 Từ (1) và (2), ta có:    0.5 3a  b  0 b  3
Bài 4 (1.5 điểm). Tìm m để phương trình: 2 x  m   2 2 2 x  m  2  0 có hai 1.5
nghiệm x , x thỏa điều kiện 2 2 x  x  x x  46 . 1 2 1 2 1 2 Ta có:   m  2 '   2 2 m  2  4m  2
Để PT đã cho có hai nghiệm x , x thì: 1 2 0.5 1 '
  0  4m  2  0  m     1 . 2 x  x  2  m  2 1 2   4
Theo Định lý Vi-ét, ta có:  2 x x  m  2 0.25  1 2
Mà: x  x  x x  46   x  x 2 2 2  3x x  46 1 2 1 2 1 2 1 2    m   2     2 m   2 2 2 3
2  46  m 16m  36  0 0.5  m  2   m  1  8
Kết hợp với (1), ta có: m  2 0.25
Bài 5 (1.0 điểm). Giải phương trình: √x − 2x + 9 + √x − 2x + 4 = 5 1.0
Đặt t = √x − 2x + 4 (t ≥ √3) 0.75 5
Phương trình trở thành: √t + 5 + t = 5  5 − t ≥ 0  t ≤ 5 t + 5 = (5 − t) t = 2
Với t = 2 => x = 0 hay x = 2 0.25
Bài 6 (3.0 điểm). Trong mặt phẳng tọa độ cho 3 điểm A 1  ; 3   , B2;  1 , 6 3.0 C  6  ;7 .
a) Chứng minh rằng tam giác ABC
vuông. Tính diện tích và chu vi tam 1.0 giác ABC .  Ta có: AB    2 2
3; 4  AB  3  4  25  5  AC     AC   2 2 5;10 5 10  125  5 5  0.5 BC     BC   2 2 8;6 8  6  100  10 Vậy: 2 2 2
AB  BC  25 100  125  AC ; Hay tam giác ABC vuông tại B
*) Tính diện tích tam giác: 1 1 S  A . B BC  .5.10  25 . ABC 2 2 0.5
*) Tính diện tích và chu vi tam giác:
2 p  AB  AC  BC  5  5 5 10  5(3  5) .
b) Tìm tọa độ trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC . 1.0
*) Tìm tọa độ trọng tâm G của tam giác ABC là:  x  x  x 1 2  6 5 A B C x     G  3 3 3  5 5    G ;   y  y  y 3 1 7 5   3 3  A B C y    G  3 3 3
*) Tìm tâm I của đường tròn ngoại tiếp tam giác ABC : 0.5
Do tam giác ABC vuông tại B nên I là trung điểm của AC :  x  x 1 6 7 A C x     I  2 2 2  7     I ; 2   . y  y 3  7   2  A C y    2 I  2 2   c) Tính cosA ;
B OC  với O là gốc tọa độ. 1.0   AB  3;4;OC   6  ;7 0.5     A . B OC 3. 6  4.7 10 2 85 cos A ; B OC   
      0.5 AB . OC 5. 62 2 5 85 85  7
(Mọi cách làm đúng khác đều đạt điểm tối đa)