Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường Phong Phú – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường Phong Phú, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem
Preview text:
SỞ GIÁO DỤC VÀ ĐẠO TẠO TP. HCM ĐỀ KIỂM TRA HỌC KÌ I TRƯỜNG THPT PHONG PHÚ NĂM HỌC: 2019- 2020 MÔN: Toán- KHỐI 10
Thời gian làm bài: 90 phút
( không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Câu 1: (1 điểm) Tìm TXĐ của các hàm số sau: x 2 a. y b. y 3x 4 2 x 2x 3
Câu 2: (2 điểm) Cho hàm số 2 y x 2x 3 (P),
a. Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số đã cho
b. Dựa vào đồ thị (P), tìm các giá trị của tham số m để phương trình 2
x 2x 3 m 1 có hai nghiệm phân biệt.
Câu 3: (2 điểm) Giải các phương trình sau: 2 x x 2 a. 10 x 2 b. 4x 1 x 1
c. x 2 x 1 2x 3
Câu 4: (1 điểm) Cho phương trình 2 2
x (1 3m)x 2m 2m 0 . Tìm các giá trị của tham số m để
phương trình có hai nghiệm dương phân biệt.
Câu 5: ( 1 điểm) Bốn anh em chia với nhau 45 triệu đồng. Nếu cho thêm người thứ nhất 2 triệu đồng,
lấy đi của người thứ hai 2 triệu đồng, gấp đôi số tiền của người thứ ba, giảm một nửa số tiền người thứ
tư thì bốn anh em sẽ có số tiền đều nhau. Hỏi lúc đầu mỗi người nhận được bao nhiêu tiền?
Câu 6: (2 điểm) Cho tam giác ABC, biết A (2; 1), B (-1; 2), C (3; -2)
a. Chứng minh rằng tam giác ABC là tam giác cân.
b. Tính chu vi và diện tích tam giác ABC.
c. Tìm tọa độ điểm D thuộc Ox sao cho tam giác ABD vuông tại D 5 Câu 7: ( 1 điểm) Cho 0 0 sin
0 90 . Tính các giá trị lượng giác còn lại. 13
------------------- HẾT ------------------
Họ và tên học sinh: ............................................................................... . SBD: ..................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM TRƯỜNG THPT PHONG PHÚ
ĐÁP ÁN VÀ THANG ĐIỂM CHI TIẾT - TOÁN 10
ĐỀ KỂM TRA HỌC KÌ I- NĂM HỌC 2019- 2020 ĐỀ CHÍNH THỨC THANG CÂU ĐÁP ÁN CHI TIẾT ĐIỂM x 2 a. y 2 x 2x 3 ĐKXĐ: 2 x 2x 3 0 x 1 0, 25 x 3 1 Vậy TXĐ: D R \ 1 ; 3 0, 25 b. y 3x 4 4
ĐKXĐ: 3x 4 0 x 3 0, 25 4 Vậy TXĐ: D ; 3 0, 25 a. 2 y x 2x 3 TXĐ: D = R 0, 25 Ta có: b 1; 4 2a 4a BBT: x 1 y 0, 5 -4 2
Hàm số nghịch biến trên khoảng ; 1
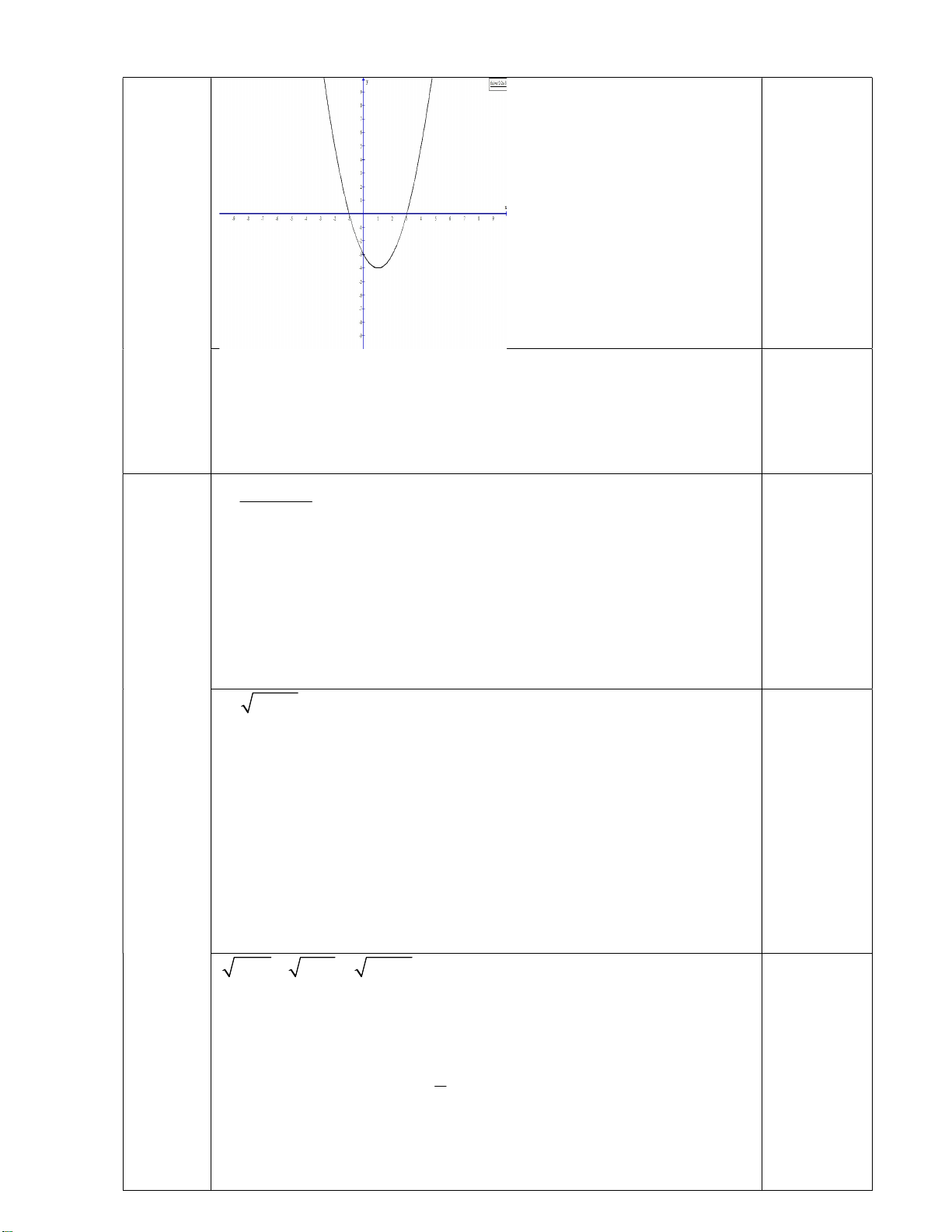
Hàm số đồng biến trên khoảng 1; Đỉnh I (1; -4) 0, 25 Trục đối xứng: x = 1 Bảng giá trị: x 0 -1 3 2 0, 25 y -3 0 0 -3 Đồ thị: 0, 25 b. 2 x 2x 3 m 1 (*) y m 1 0, 25
Dự vào đồ thị (P), để phương trình (*) có hai nghiệm phân biệt thì : m 1 4 0, 25 m 3 2 x x 2 a. 10 (1) x 2
ĐKXĐ: x 2 0 x 2 0, 25 2
(1) x x 2 10(x 2) 2 x 9x 22 0 0, 25 x 11 x 2 (loai) Vậy S = {11} 0, 25 b. 4x 1 x 1 x 1 0 0, 25 4x 1 x 12 x 1 0, 25 2 3 x 2x 0 x 1 x 0 (n) 0, 25 x 2 (n) Vậy S = {0; 2}
x 2 x 1 2x 3 (3) x 2 0 x 2
ĐKXĐ: x 1 0 x 1 x 2 0, 25 2x 3 0 3 x 2
(3) x 2 x 1 2 (x 2)(x 1) 2x 3 2 2 x 3x 2 0 2 x 3x 2 0 0, 25 x 1 (l) x 2 (n) Vậy S = {2} 2 2
x (1 3m)x 2m 2m 0 Theo vi- ét, ta có: S x x 1 3m 1 2 0, 25 2 P x .x 2m 2m 1 2
Để phương trình có hai nghiệm dương phân biệt thì: 0 0, 25 S 0 P 0 4 m 12 0 2 m 1 m 2m 1 0 1 1 1 3m 0 m m 3 3 0, 25 2 2m 2m 0 m 0 m 0 m 1 m 1 m 1 m 0 0, 25 m 1 Vậy
thì phương trình có hai nghiệm dương phân biệt m 0
Gọi x, y, z lần lượt là số tiền của người thứ nhất, thứ hai, thứ ba (đơn vị: triệu) 0, 25 ĐK: 0 x, y, z 45
Khi đó số tiền của người thứ tư là [45- ( x + y + z)] (triệu) 0, 25 Theo giả thiết, ta có: 45 (x y z) x 2 y 2 2z 2 2z x 2 5 2z y 2 45 (x y z) 0, 25 2z 2 x -2z 2 x 8
y -2z = 2 y 12 x + y + 5z = 45 z 5
Vậy số tiền của người thứ nhất, thứ hai, thứ ba, thứ tư lần lượt là: 8 0, 25
triệu, 5 triệu, 12 triệu, 20 triệu. A(2;1); B(1;2); C(3;2) a. Ta có: AB ( 3 ;1) AB 10 0, 5 AC (1;3) AC 10 BC (4; 4 ) BC 4 2
Vì AB AC 10 nên tam giác ABC cân tại A 0, 25
b. Chu vi của tam giác ABC: AB AC BC 2 10 4 2 0, 25
Gọi H x ;y là trung điểm BC H H H(1;0) 0, 25
Ta có: AH (1;1) AH 2 6 1 1
Diện tích của tam giác ABC là: S BC.AH .4 2. 2 4 2 2 0, 25 c. D Ox D(x ;0) D 0, 25
Ta có: DA 2 x ;1 ; DB 1 x ;2 D D
Theo giả thiết, tam giác ABD vuông tại D DA.DB 0 (2 x )( 1 x ) 2 0 D D 2 x x 2 0 D D x 1 D 0, 25 x 2 D Vậy D(-1; 0) hoặc D(2; 0) 5 0 0 sin 0 90 13 Ta có: 2 2 sin cos 1 2
cos 1 sin 0, 25 2 5 12 7 = 1 13 13 12 Vì 0 0
0 90 cos 13 sin 5 0, 25 tan cos 12 0, 25 12 cot 5 0, 25