

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019- 2020 TRƯỜNG THPT BÁCH VIỆT Môn thi: Toán 10 _________
Thời gian làm bài: 90 phút Đề thi chính thức
(không kể thời gian giao đề) Đề thi có 1 trang Ngày thi: 21/ 12 /2019
Câu 1 (0.5 điểm): Viết mệnh đề phủ định của các mệnh đề sau:
a. A: “ 5 là một số vô tỉ.” b. B: “ 2 x
[ 1,3]: 3x 10x 3 0 ”.
Câu 2 (0.5 điểm): Cho tập hợp A x Z || x 1|
3 , B={0;1;2;4;5;6}. Xác định A B, A \ B .
Câu 3 (1 điểm): Cho A 1 2; 3 , B x R | 1 x 7 . Tìm A , B A , B A \ , B C A. R
Câu 4 (1 điểm): Tìm tập xác định của các hàm số sau: a. y 4x 10 b. y x 5 5 x
Câu 5 (0.5 điểm): Xét tính chẵn, lẻ của hàm số sau: 3 y f (x) x 3x
Câu 6 (1 điểm): Viết phương trình dạng y=ax+b của đường thẳng đi qua hai điểm A(2;1) và B(-1;-1).
Câu 7 (1 điểm): Cho parabol (P): 2 y x 2x 3 . a. Khảo sát và vẽ (P).
b. Tìm m để đường thẳng d: y=2m+5 cắt (P) tại hai điểm phân biệt.
Câu 8 (1.5 điểm): Giải các phương trình sau: a. 3x 4 x 3 b. | 2x 5 | 1 3x c. 2 2x 3x 4 7x 2
Câu 9 (2.5 điểm): Trong mặt phẳng tọa độ Oxy, cho A(1;-3), B(2;5), C(0;7).
a. Chứng minh ba điểm A, B, C lập thành tam giác. Tính A . B AC
b. Tìm tọa độ trung điểm I của đoạn thẳng BC, tọa độ trọng tâm G của tam giác ABC.
c. Tìm tọa độ điểm D để ABCD là hình bình hành.
d. Tìm tọa độ trực tâm H của tam giác ABC.
Câu 10 (0.5 điểm): Cho tam giác ABC. Chứng minh rằng với điểm M tuỳ ý ta có
M . A BC M . B CA MC.AB 0 -----------HẾT-------------
Thí sinh không được sử dụng tài liệu
Giám thị không giải thích gì thêm
Họ và tên học sinh: ................................................ Số báo danh: ..................... ...................
Chữ ký của giám thị 1: .......................................... Chữ ký của giám thị 2 ..........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI MÔN TOÁN THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA HỌC KỲ I LỚP 10 TRƯỜNG THPT BÁCH VIỆT NĂM HỌC 2019 – 2020 _________ ĐỀ THI CHÍNH THỨC
(Bản Hướng dẫn chấm thi gồm 3 trang) Câu Nội dung Điểm Câu 1:
a. A: “ 5 không phải là số vô tỉ” 0.25 điểm 0.5 điểm b. B : “ 2 x
[ 1,3]: 3x 10x 3 0” 0.25 điểm Câu 2: A B 1 ;0;1;2;3; 4;5; 6 0.25 điểm 0.5 điểm A \ B 1; 3 0.25 điểm Câu 3: A B [ 12;7] 0.25 điểm 1 điểm A B (1;3] 0.25 điểm A \ B [ 12; 1] 0.25 điểm 0.25 điểm C A ( ; 1 2) (3;) R Câu 4: a. 5 0.25 điểm x 1 điểm 2 5 0.25 điểm D ; 2 b. 5 x 5 D=[-5;5] 0.25 điểm 0.25 điểm Câu 5 3
f (x) (x) 3(x) f (x) 0.25 điểm 0.5 điểm
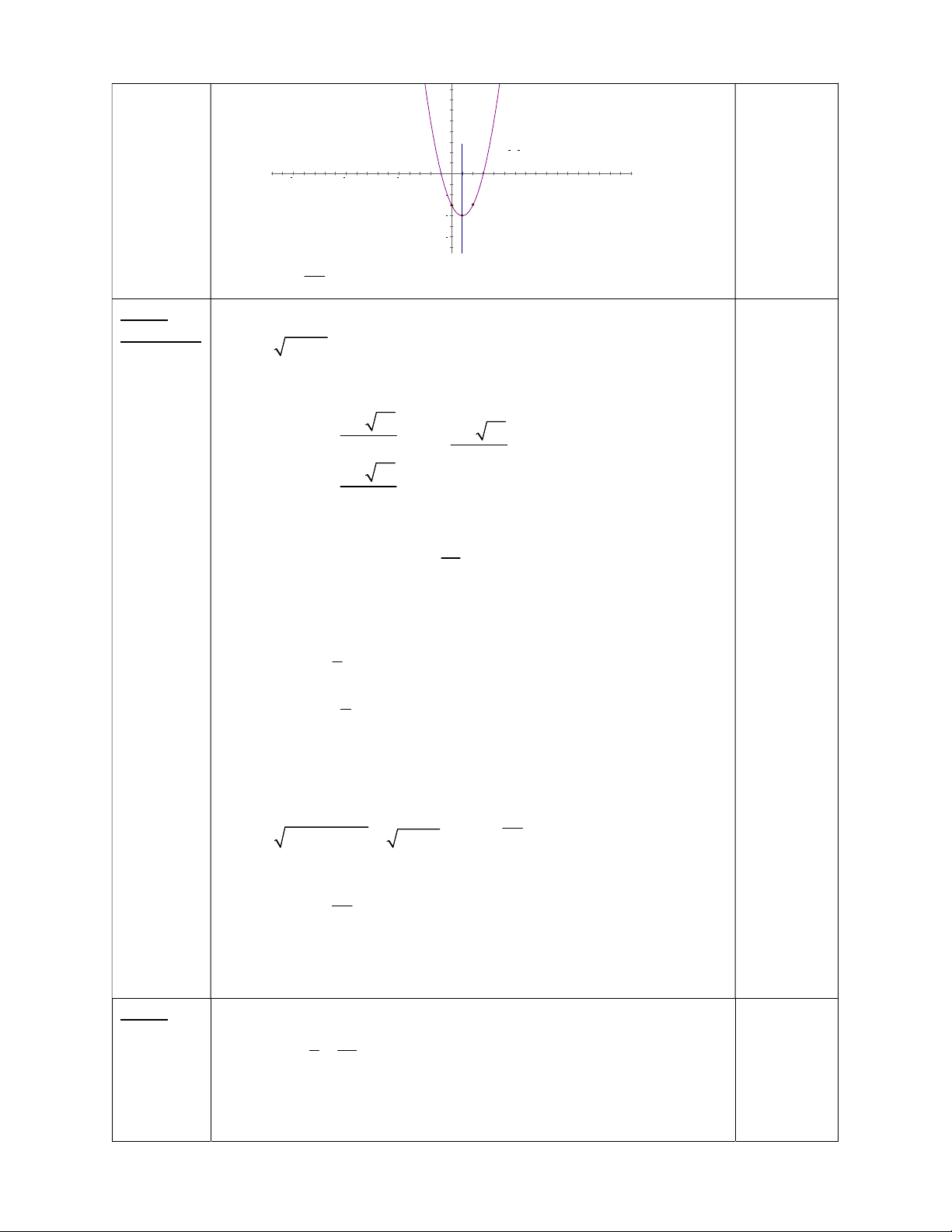
Hàm số y=f(x) là hàm lẻ 0.25 điểm Câu 6 2a b 1 0.5 điểm 1 điểm a b 1 2 a 3 0.25 điểm 1 b 3 2 1 y x 3 3 0.25 điểm Câu 7 a. I(1;-4) 0.25 điểm Lập bảng biến thiên x 1 y -4 Điểm đặc biệt x -1 0 1 2 3 y 0 -3 -4 -3 0 0.25 điểm Vẽ parabol 8 6 4 x=1 f x ( ) = x2 2∙x 3 2 0.25 điểm 15 10 5 5 10 15 2 4 6 b. 9 m 0.25 điểm 2 Câu 8 a. (1.5 điểm) x 3 0 3x 4 x 3 2 3 0.25 điểm x 4 (x 3) x 3 9 29 x 9 29 2 x 2 0.25 điểm 9 29 x 2 b. 1 x 3 0.25 điểm
| 2x 5 | 1 3x 2x 5 13x
2x 5 1 3x 1 x 3 6 x 4 x 5 0.25 điểm x 4 c. 2 x 2
2x 3x 4 7x 2 7 0.25 điểm 2
2x 3x 4 7x 2 2 x 7 x 3 x 3 x 1 0.25 điểm Câu 9 a. AB (1;8), AC ( 1 ;10) 0.25 điểm Ta có 1 1
nên ba điểm A,B,C lập thành một tam giác 8 10 0.25 điểm 0.5 điểm A . B AC 1 80 79 b. I(1;6) 0.25 điểm G(1;3) 0.25 điểm
c. Để ABCD là hình bình hành thì AB DC 0.25 điểm x 1 D 0.25 điểm y 1 D
d. Để H là trực tâm của tam giác ABC thì AH.BC 0 0.25 điểm BH.AC 0 88 x H 9 0.25 điểm 52 y H 9
Câu 10 M . A BC M . A (MC MB) M . A MC M . A MB 0.5 điểm
M . B CA M . B (MA MC) M . B MA M . B MC
0.25 điểm MC.AB MC.(MB M ) A MC.MB MC.MA
M . A BC M . B CA MC.AB 0 0.25 điểm --- HẾT ---




