Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Hiệp Bình – TP HCM

Giới thiệu đến thầy, cô và các em học sinh đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Hiệp Bình, thành phố Hồ Chí Minh. Đề thi với cấu trúc 100% tự luân, mời bạn đọc đón xem

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT HIỆP BÌNH
ĐỀ KIỂM TRA HỌC KÌ I
KHỐI 10 - NĂM HỌC 2019-2020
MÔN : TOÁN - Thời gian: 90 phút
(không kể thời gian phát đề)
Câu 1 (0,5 điểm): Tìm tập xác định của hàm số:
2
3
1
x x
y
x
x
Câu 2 (1,5 điểm): a) Lập bảng biến thiên và vẽ đồ thị của hàm số:
2
2 3
y x x
b) Tìm hàm số bậc hai:
2
5
y ax bx
biết đồ thị của nó có phương trình trục đối xứng là
2
x
và
đi qua điểm
1;5
A
.
Câu 3 (3 điểm): Giải các phương trình sau:
a)
2
2 3
x x x
b)
2
2 4 3
x x x
c)
3 2 1 2
2
2 1
x x
x x
d)
2 2 1 2 3 5
x x x
Câu 4 (1 điểm): Một nhà máy trang bị hai máy công cụ chuyên sản xuất bạc đạn xe máy. Ngày thứ
nhất cả hai máy làm được 930 bạc đạn. Ngày thứ hai, do máy thứ nhất tăng năng suất
18%
, máy thứ
hai tăng năng suất
15%
nên cả hai máy làm được 1083 bạc đạn. Hỏi trong ngày thứ nhất mỗi máy
công cụ làm được bao nhiêu bạc đạn xe máy?
Câu 5 (3 điểm): Trên mặt phẳng tọa độ Oxy cho tam giác
ABC
có
1; 2
A
,
1; 3
B
,
2; 1
C
.
a) Tính tọa độ của véc tơ
u AB AC
b) Tìm tọa độ trọng tâm
G
của tam giác
ABC
c) Chứng minh rằng tam giác
ABC
vuông cân tại
B
d) Tính góc giữa hai véc tơ
BC
và
CA
e) Tìm điểm
M
trên trục hoành sao cho tam giác
BMC
cân tại
M
.
Câu 6 (0,5 điểm): Cho phương trình:
2
1 2 1 2 0
m x m x m
. Tìm tham số
m
để phương
trình có hai nghiệm phân biệt
1
x
,
2
x
thỏa mãn:
1 2 1 2
4 7
x x x x
Câu 7 (0,5 điểm): Chứng minh rằng với mọi số thực
,
x
,
y
z
ta luôn có:
2 2 2
2
x y z xy yz zx
Dấu đẳng thức xảy ra khi nào?
----HẾT----
Họ và tên học sinh: .........................................................
Lớp: ................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT HIỆP BÌNH
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ I
KHỐI 10 - NĂM HỌC 2019-2020
MÔN : TOÁN - Thời gian: 90 phút
(không kể thời gian phát đề)
CÂU
NỘI DUNG ĐIỂM
1
Đ/k:
1 0 1
3 0 3
x x
x x
TXĐ:
1; \ 3
D 
0.5
2
a) TXĐ:
D
Đỉnh:
1;4
I
Trục đối xứng:
1
x
Giao điểm với trục tung
0;3
. Mặt khác:
2
3
2 3 0
1
x
x x
x
Bảng biến thiên:
Đồ thị:
1.0
y
x
b)
2
5 ( 1) ( 1) 5
2
2
a b
b
a
2
10 2
2 8 5
4 0 8
a b a
y x x
a b b
0.5
3
a)
2
2
3 0
3 0
3 0
7
5 7 0
( )
2 3
5
x
x
x
x
x l
x x x
0.75
b)
2
2
2
2
1 17
2
2 4 3
4 0
1 17
2
2 4 3
5 4 0
1
4
x
x x x
x x
x
x x x
x x
x
x
0.75
c) Đ/k:
2 0
1 0
x
x
3 2 1 (1 2 )( 2) 2( 2)(1 )
pt x x x x x x
2
3 0 0( )
x x n
1
d)
2 2
3 1 2 2 2 4(3 5) 2 2 2 9 19
x x x x x
2
3
73 342 369 0
123
73
x
x x
x
. Thử lại ta có:
3( )
123
( )
73
x n
x l
0.5
4
Gọi x (cái) là số bạc đạn máy 1 làm được trong ngày thứ nhất
y (cái) là số bạc đạn máy 2 làm được trong ngày thứ nhất
, 0
x y
930 450
0.18 0.15 1083 480
x y x
x x y y y
1
5
a)
(2; 1), 3;1 , 5;0
AB AC u
0.5
b)
2
; 2
3
G
0.5
c)
1;2 , 5, 5,
BC AB BC AB BC ABC
cân tại B (1)
mà
2.1 ( 1).2 0
AB BC
(2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại B
1
d)
(1;2), ( 3; 1),
BC CA
0.5
0
2 2
2 2
1( 3) 2( 1) 5
os , , , 135
50
1 2 . 3 1
c BC CA BC CA
 
e)
2 2
( ,0), 2 10, 4 5,
M x BM x x CM x x BM CM
5 5
2 10 4 5 ;0
2 2
x x x M
0.5
6
12 4
m
. Pt có hai nghiệm phân biệt
1 0 1
12 4 0 3
m m
m m
1 2
1 2
2 1
1
2
1
m
x x
m
m
x x
m
đáp số m=-6(nhận)
0.5
7
2 2
2
2 ( ) 0 0
x y z z x y x y z
, đúng, đpcm
Dấu “=” có khi
0
x y z y x z
0.5
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KÌ I THÀNH PHỐ HỒ CHÍ MINH
KHỐI 10 - NĂM HỌC 2019-2020 TRƯỜNG THPT HIỆP BÌNH
MÔN : TOÁN - Thời gian: 90 phút
(không kể thời gian phát đề) x 2x
Câu 1 (0,5 điểm): Tìm tập xác định của hàm số: y   x 1 x  3
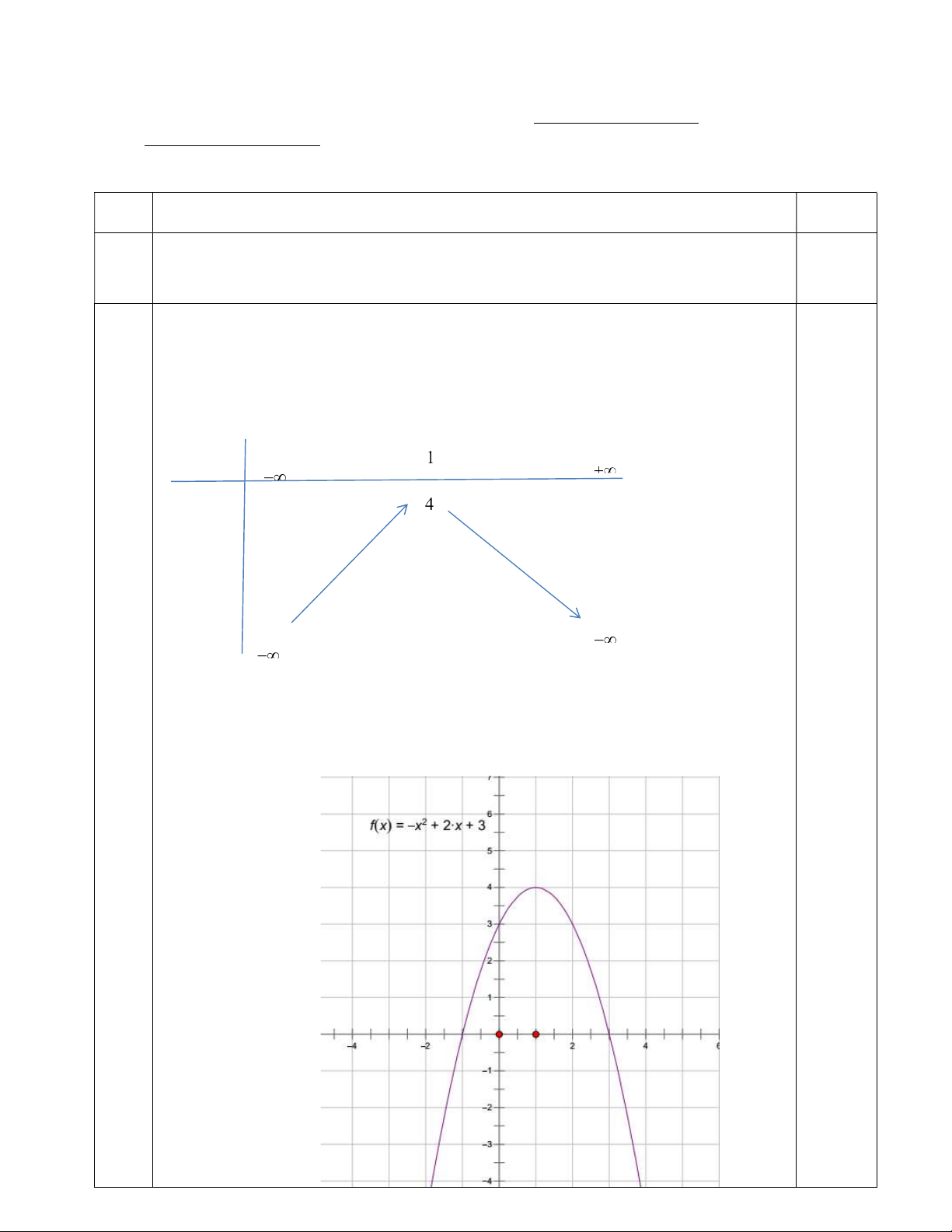
Câu 2 (1,5 điểm): a) Lập bảng biến thiên và vẽ đồ thị của hàm số: 2 y  x  2x  3 b) Tìm hàm số bậc hai: 2
y  ax  bx  5 biết đồ thị của nó có phương trình trục đối xứng là x  2 và đi qua điểm A 1  ;  5 .
Câu 3 (3 điểm): Giải các phương trình sau: a) 2 x  x  2  x  3 b) 2 x  2x  4  3x   c) 3x 2 1 2x 
 2 d) 2x  2  x 1  2 3x  5 x  2 1 x
Câu 4 (1 điểm): Một nhà máy trang bị hai máy công cụ chuyên sản xuất bạc đạn xe máy. Ngày thứ
nhất cả hai máy làm được 930 bạc đạn. Ngày thứ hai, do máy thứ nhất tăng năng suất 18% , máy thứ
hai tăng năng suất 15% nên cả hai máy làm được 1083 bạc đạn. Hỏi trong ngày thứ nhất mỗi máy
công cụ làm được bao nhiêu bạc đạn xe máy?
Câu 5 (3 điểm): Trên mặt phẳng tọa độ Oxy cho tam giác ABC có A 1  ; 2   , B1;  3 , C 2;  1 .   
a) Tính tọa độ của véc tơ u  AB  AC
b) Tìm tọa độ trọng tâm G của tam giác ABC
c) Chứng minh rằng tam giác ABC vuông cân tại B  
d) Tính góc giữa hai véc tơ BC và CA
e) Tìm điểm M trên trục hoành sao cho tam giác BMC cân tại M .
Câu 6 (0,5 điểm): Cho phương trình: m   2 1 x  2m  
1 x  m  2  0. Tìm tham số m để phương
trình có hai nghiệm phân biệt x , x thỏa mãn: 4x  x  7x x 1 2  1 2 1 2
Câu 7 (0,5 điểm): Chứng minh rằng với mọi số thực x, y, z ta luôn có: 2 2 2
x  y  z  2 xy  yz  zx
Dấu đẳng thức xảy ra khi nào? ----HẾT----
Họ và tên học sinh: .........................................................
Lớp: ................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ I THÀNH PHỐ HỒ CHÍ MINH
KHỐI 10 - NĂM HỌC 2019-2020 TRƯỜNG THPT HIỆP BÌNH
MÔN : TOÁN - Thời gian: 90 phút
(không kể thời gian phát đề) CÂU NỘI DUNG ĐIỂM x 1  0 x  1 1 Đ/k:   
TXĐ: D  1; \   3 0.5 x  3  0 x  3
a) TXĐ: D   Đỉnh: I 1;4 Trục đối xứng: x  1 Giao điểm với trục tung 0;  3 x  3 . Mặt khác: 2
x  2x  3  0   x   1 Bảng biến thiên: x y 2 1.0 Đồ thị: 2 5  a( 1  )  b(1)  5 a  b  10 a  2 b)  b 2      y  2x  8x  5 0.5   2  4a  b  0 b  8   2a x  3  0 x  3  0  x  3  0  a)       0.75 x  x  2   x  2 7 2 3 5x  7  0 x  (l)  5  1 17 x  2  2 2 x  2x  4  3x x  x  4  0    b) 1 17       x  0.75 2  x  2x    4  3x 2 x   5x  4  0  2  x  1  x  4 3 x  2  0 c) Đ/k: 
pt  3x  21 x  (1 2x)(x  2)  2(x  2)(1 x) 1   x  0 1 2
 3x  0  x  0(n) d) 2 2
 3x 1 2 2x  2  4(3x  5)  2 2x  2  9x 19 x  3 x  3(n) 2 73x 342x 369 0        123 . Thử lại ta có:  0.5  123 x  x  (l)  73  73
Gọi x (cái) là số bạc đạn máy 1 làm được trong ngày thứ nhất
y (cái) là số bạc đạn máy 2 làm được trong ngày thứ nhất x, y  0 4 x  y  930 x  450    1
x  0.18x  y  0.15y  1083  y  480    a) AB  (2; 1  ), AC  3;  1 ,u  5;0 0.5 b)  2  G ;2   0.5  3  
c) BC  1;2, AB  5, BC  5, AB  BC  A  BC cân tại B (1) 5  
mà 2.1 (1).2  0  AB  BC (2) 1
Từ (1) và (2) suy ra tam giác ABC vuông cân tại B  
d) BC  (1;2), CA  (3; 1  ), 0.5         c BC CA 1( 3) 2( 1) 5 os ,   , BC,CA  135 2 2   0 2 2       50 1 2 . 3 1 e) 2 2
M (x,0), BM  x  2x 10, CM  x  4x  5, BM  CM 5  5  0.5
 2x 10  4x  5  x    M  ;0   2  2  m 1  0 m  1 
  12  4m . Pt có hai nghiệm phân biệt     1  2  4m  0 m  3 6  2m   1 x  x  0.5  1 2  m  1  đáp số m=-6(nhận) m  2 x x  1 2  m  1
  x  y2  z  z x  y   x  y  z2 2 2 ( ) 0  0 , đúng, đpcm 7
Dấu “=” có khi x  y  z  0  y  x  z 0.5