Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Phú Hòa – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Phú Hòa, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
TRƯỜNG THPT PHÚ HÒA
ĐỀ THI HỌC KÌ 1 NĂM HỌC 2019 - 2020
TỔ TOÁN
MÔN THI: TOÁN – LỚP: 10
ĐỀ CHÍNH THỨC
Ngày thi: 19/12/2019 – Thời gian: 90 phút
Câu 1 (2,0 điểm). Tìm tập xác định của hàm số:
a)
2 3
1
x
y
x
b)
2
2
y x x
c)
6
3
y
x
d)
2
( 1) 3 9
( 4 12) 2
x x
y
x x x
Câu 2 (1,5 điểm).
a) Tìm phương trình đường thẳng
:
d y ax b
biết đường thẳng
d
đi qua hai điểm
(2;6)
M
và
( 1; 15)
N
.
b) Vẽ parabol
2
4 5
y x x
.
c) Tìm
, ,
a b c
biết parabol
2
0)
(y ax bx c a
có đỉnh
(3;2)
I
và đi qua điểm
(5; 6)
A
.
Câu 3 (2,5 điểm). Giải phương trình:
a)
2 1 1 4
x x x
b)
2
5 6
x x
c)
2
3 2 6
x x x
d)
2 2
5 6 4 19
5 5
x x
x x
e)
2
2 5 12
7 0
4 6
x x
x
x
Câu 4 (1,5 điểm). Trong mặt phẳng tọa độ
Oxy
, cho hai vectơ
(5; 3), ( 2;7)
a b
và hai điểm
(1;1)
P
,
(4; 2)
Q
.
a) Tính tọa độ của vectơ
QP
và độ dài của vectơ
b
.
b) Tìm tọa độ điểm
M
sao cho
P
là trung điểm của đoạn thẳng
MQ
.
c) Tính
cos ,
OP a
.
Câu 5 (1,0 điểm). Cho tam giác
ABC
có
7 , 8 , 9
AB a BC a AC a
.
a) Tính diện tích tam giác
ABC
.
b) Tính bán kính đường tròn ngoại tiếp tam giác
ABC
và
cos
ACB
.
Câu 6 (0,5 điểm). Một trường THPT có tổng số học sinh khối 10, khối 11 và khối 12 là
1378
học
sinh. Tổng số học sinh khối 10 và khối 11 bằng
38
15
số học sinh khối 12. Biết rằng 3 lần số
học sinh khối 12 nhiều hơn 2 lần số học sinh khối 10 là
106
học sinh. Hỏi mỗi khối có bao
nhiêu học sinh?
Câu 7 (1,0 điểm).
a) Tìm
m
để phương trình
2 2
(3 2 ) 2 0
x m x m m
có hai nghiệm phân biệt
1 2
,
x x
sao
cho
2 2
1 2 1 2
2 . 3 3 83
x x x x
.
b) Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
(2;4)
M
và
(3; 2)
N
. Tìm tọa độ điểm
I
sao
cho
. 50
MN IN
và
2 17
IN
, biết tung độ điểm
I
là số nguyên.
Hết
Câu 1a). ĐKXĐ:
1 0 1
x x
0,25
TXĐ:
\{1}
D
0,25
Câu 1b). ĐKXĐ:
2 0 0
x x
0,25
TXĐ:
[0; )
D

0,25
Câu 1c). ĐKXĐ:
6 0 6
3 0 3
x x
x x
0,25
TXĐ:
( 3;6]
D
0,25
Câu 1d). ĐKXĐ:
2
3
3 9 0
2
2 0
6
4 12 0
2
x
x
x
x
x
x x
x
0,25
TXĐ:
[ 3;2) \{ 2}
D
0,25
Câu 2a). Ta có
2 6
15
a b
a b
0,25
7
8
a
b
Vậy
: 7 8
d y x
0,25
Câu 2b). Đỉnh parabol
( 2;1)
I
0,25
BGT
x
4
3
2
1
0
y
5
2
1
2
5
0,25
Câu 2c). Ta có
9 3 2
25 5 6
3
2
a b c
a b c
b
a
2
12
16
a
b
c
0,25 +0,25
Câu 3a). ĐK
1
x
Pt
2 4 2
x x
0,25
So với đk, pt đã cho vô nghiệm. 0,25
Câu 3b).
2 2
5 6 5 36
x x x x
0,25
9
4
x
x
là nghiệm của pt
0,25
Câu 3c).
2
3 2 6
x x x
2
0
3 2 6
x
x x x
0,25
0
1
3
x
x
x
Vậy pt có nghiệm duy nhất
1
x
0,25
Câu 3d). ĐK:
5
x
x
y
5
4
3
2
1
0
-1
-2
-3
-4
Pt
2
5
25 0
5
x
x
x
0,25
So đk, pt có 1 nghiệm
5
x
0,25
Câu 3e). ĐK:
3
2
x
Pt
2
6
6 27 54 0
3
2
x
x x
x
0,25
So đk, pt có 1 nghiệm
6
x
0,25
Câu 4a).
( 3;3)
QP
,
53
b
0,25 + 0,25
Câu 4b).
P
là trung điểm của
MQ
4
1
2
( 2)
1
2
M
M
x
y
2
4
M
M
x
y
. Vậy
( 2;4)
M
0,25
Câu 4c).
2 2
1.5 1.( 3)
cos ,
1 1. 5 3
OP a

17
17
0,25 + 0,25
Câu 5a).
7 8 9
12
2
a a a
p a
,
( 7 )( 8 )( 9 )
ABC
S p p a p a p a
0,25
2
12 5
a
0,25
Câu 5b).
. . 21 5
4 10
ABC
AB BC AC
R a
S
0,25
2 2 2
(8 ) (9 ) (7 ) 2
cos
2.8 .9 3
a a a
ACB
a a
0,25
Câu 6). Gọi
, ,
x y z
lần lượt là số học sinh khối 10, khối 11, khối 12. (đk:
, ,x y z
)
Ta có
1378
38
15
3 2 106
x y z
x y z
z x
532
456
390
x
y
z
0,25+0,25
Câu 7a). Pt có hai nghiệm phân biệt
1 2
,
x x
1
0 8 1 0
8
m m
2 2 2
1 2 1 2 1 2 1 2
2 3 3 83 3( ) 8 83
x x x x x x x x
0,25
2 2
3(3 2 ) 8( 2) 83
m m m
2
9
4 28 72 0
2
m
m m
m
Vậy
2
m
thỏa yêu cầu bài toán.
0,25
Câu 7b). Gọi
( ; )
I x y
2 2
6 35
. 50
(38 6 ) ( 2) 68
2 17
x y
MN IN
y y
IN
0,25
2
6 35
6 35
6 ( )
37 452 1380 0
230
( )
37
x y
x y
y n
y y
y l
Vậy
(1;6)
I
0,25
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT PHÚ HÒA
ĐỀ THI HỌC KÌ 1 NĂM HỌC 2019 - 2020 TỔ TOÁN MÔN THI: TOÁN – LỚP: 10 ĐỀ CHÍNH THỨC
Ngày thi: 19/12/2019 – Thời gian: 90 phút
Câu 1 (2,0 điểm). Tìm tập xác định của hàm số: 2x  3 x  6  x (x 1) 3x  9 a) y  b) 2 y  x  2x c) y  d) y  1 x x  3 2 (x  4x 12) 2  x Câu 2 (1,5 điểm).
a) Tìm phương trình đường thẳng d : y  ax  b biết đường thẳng d đi qua hai điểm M (2;6) và N (1;15) . b) Vẽ parabol 2 y  x  4x  5 . c) Tìm a, , b c biết parabol 2
y  ax  bx  c (a  0) có đỉnh I (3;2) và đi qua điểm ( A 5; 6) .
Câu 3 (2,5 điểm). Giải phương trình:
a) 2x  x 1  x 1  4 b) 2 x  5x  6 c) 2 3x  2x  6  x 2 2 5x  6 4x 19 2 2x  5x 12 d)  e) x  7   0 5  x 5  x 4x  6  
Câu 4 (1,5 điểm). Trong mặt phẳng tọa độ Oxy , cho hai vectơ a  (5;3), b  (2;7) và hai điểm P(1;1) , Q(4; 2  ) .  
a) Tính tọa độ của vectơ QP và độ dài của vectơ b .
b) Tìm tọa độ điểm M sao cho P là trung điểm của đoạn thẳng MQ.   c) Tính cosOP,a.
Câu 5 (1,0 điểm). Cho tam giác ABC có AB  7a, BC  8a, AC  9a .
a) Tính diện tích tam giác ABC .
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC và cos  ACB .
Câu 6 (0,5 điểm). Một trường THPT có tổng số học sinh khối 10, khối 11 và khối 12 là 1378 học 38
sinh. Tổng số học sinh khối 10 và khối 11 bằng
số học sinh khối 12. Biết rằng 3 lần số 15
học sinh khối 12 nhiều hơn 2 lần số học sinh khối 10 là 106 học sinh. Hỏi mỗi khối có bao nhiêu học sinh? Câu 7 (1,0 điểm).
a) Tìm m để phương trình 2 2
x  (3  2m)x  m  m  2  0 có hai nghiệm phân biệt x , x sao 1 2 cho 2 2 2x .x  3x  3x  83 . 1 2 1 2
b) Trong mặt phẳng tọa độ Oxy , cho hai điểm M (2;4) và N(3;2) . Tìm tọa độ điểm I sao  
cho MN.IN  50 và IN  2 17 , biết tung độ điểm I là số nguyên. Hết
Câu 1a). ĐKXĐ: 1 x  0  x  1 0,25 TXĐ: D   \{1} 0,25
Câu 1b). ĐKXĐ: 2x  0  x  0 0,25 TXĐ: D  [0;) 0,25 6  x  0 x  6 Câu 1c). ĐKXĐ:    0,25 x  3  0 x  3  TXĐ: D  (3;6] 0,25 x  3  3x  9  0   x  2
Câu 1d). ĐKXĐ: 2  x  0   0,25 x  6  2  x  4x 12  0 x  2 
TXĐ: D  [3;2) \ {2} 0,25 2a  b  6 Câu 2a). Ta có  0,25 a  b  1  5 a  7   Vậy d : y  7x  8 0,25 b  8 
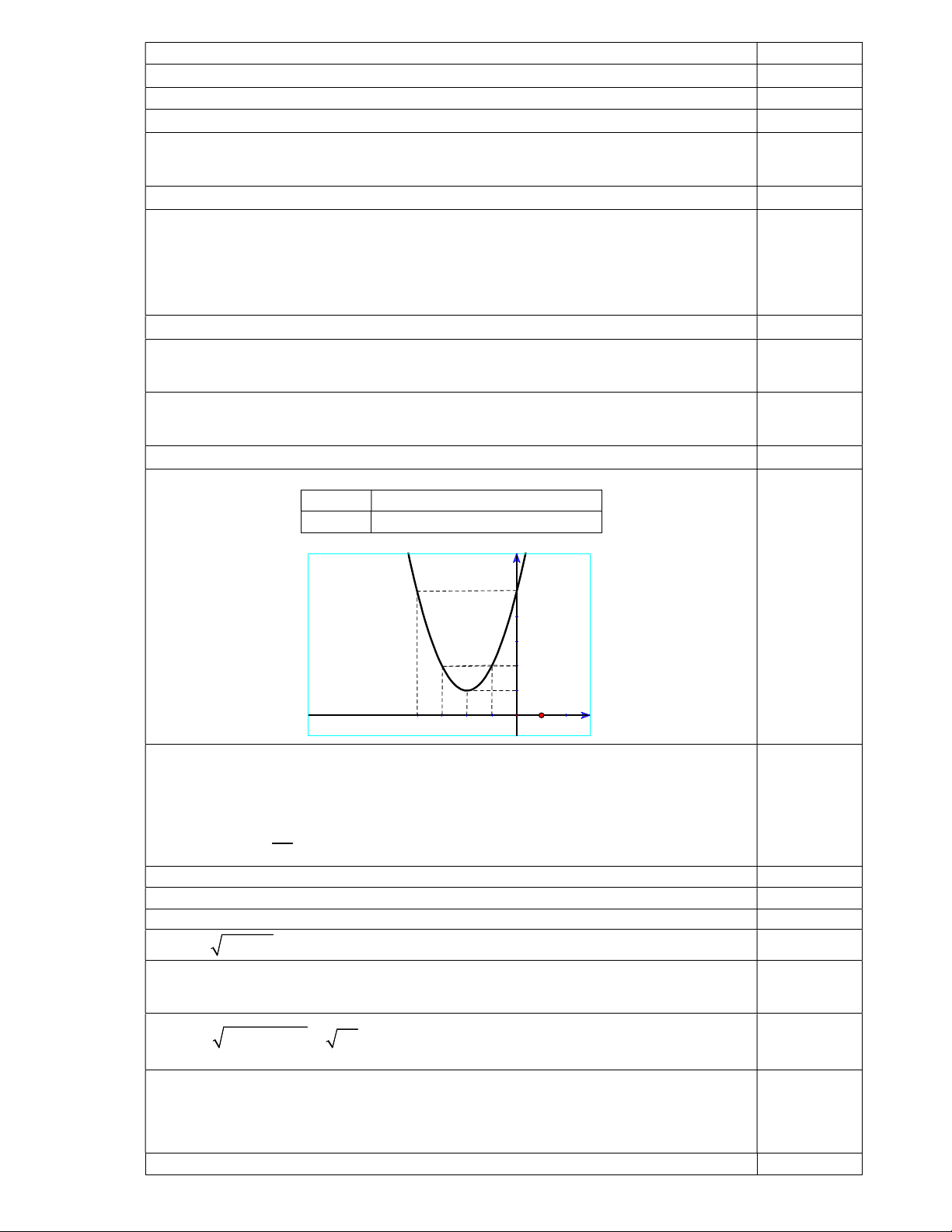
Câu 2b). Đỉnh parabol I ( 2  ;1) 0,25 BGT x 4  3  2  1 0 y 5 2 1 2 5 y 5 0,25 4 3 2 1 x -4 -3 -2 -1 0  9a  3b  c  2 a  2   
Câu 2c). Ta có 25a  5b  c  6   b   12 0,25 +0,25  b      c 16 3  2a Câu 3a). ĐK x  1  Pt  2x  4   x  2  0,25
So với đk, pt đã cho vô nghiệm. 0,25 Câu 3b). 2 2
x  5x  6  x  5x  36 0,25 x  9   là nghiệm của pt 0,25 x  4  x  0 Câu 3c). 2
3x  2x  6  x   0,25 2 3x  2x  6  x x  0   x  1
 Vậy pt có nghiệm duy nhất x  1  0,25  x  3 Câu 3d). ĐK: x  5 x  5 Pt 2  x  25  0   0,25 x  5 
So đk, pt có 1 nghiệm x  5  0,25 3 Câu 3e). ĐK: x  2 x  6 Pt 2 6x 27x 54 0       3  0,25 x    2
So đk, pt có 1 nghiệm x  6 0,25   Câu 4a). QP  ( 3  ;3) , b  53 0,25 + 0,25  x  4 1 M   x  2 
Câu 4b). P là trung điểm của 2 MQ   M   . Vậy M (2;4) 0,25 y  ( 2  ) y   4 1  M  M  2   1.5 1.( 3  ) 17 Câu 4c). cosOP,a   0,25 + 0,25 2 2 11. 5  3 17 7a  8a  9a Câu 5a). p   12a , S
 p( p  7a)( p  8a)( p  9a) 0,25 2 ABC 2  12 5a 0,25 A . B BC.AC 21 5 Câu 5b). R   a 0,25 4S 10 ABC a  a  a  2 2 2 (8 ) (9 ) (7 ) 2 cos ACB   0,25 2.8a.9a 3
Câu 6). Gọi x, y, z lần lượt là số học sinh khối 10, khối 11, khối 12. (đk: x, y, z   ) x  y  z  1378  x  532  38  Ta có x  y  z   y  456 0,25+0,25 15     z 390 3z  2x 106  1
Câu 7a). Pt có hai nghiệm phân biệt x , x    0  8  m 1  0  m  1 2 8 0,25 2 2 2
2x x  3x  3x  83  3( x  x )  8x x  83 1 2 1 2 1 2 1 2 m  9 2 2
 3(3  2m)  8(m  m  2)  83 2
 4m  28m  72  0   m  2  0,25 Vậy m  2
 thỏa yêu cầu bài toán. Câu 7b). Gọi I ( x; y)   MN.IN  50 x  6y  35 0,25    2 2 IN  2 17 (38 
 6 y)  ( y  2)  68 x  6 y  35 x 6 y 35     y  6 (n)     Vậy I (1;6) 0,25 2 37 y 452 y 1380 0      230  y  (l)  37