Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Phước Kiển – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Phước Kiển, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG TRUNG HỌC PHỔ THÔNG
PHƯỚC KIỂN
ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
Môn: Toán . Lớp: 10
Thời gian làm bài: 90 phút
(Không k
ể
th
ờ
i gian phát phát đ
ề
)
(ĐỀ CHÍNH THỨC)
Câu 1: (1,0 điểm) Xác định hàm số
2
:
P y x bx c
, biết đồ thị của hàm số
P
đi qua điểm
2;0
A
và có trục đối xứng là
5
x
.
Câu 2: (2,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2
2 4 2
y x x
.
Câu 3: (3,0 điểm) Giải các phương trình sau:
a)
2
3 6 19 4 8
x x x
b)
2
2 7 4 7
x x
c)
7 2 3 3
x x
Câu 4: (1,0 điểm) Cho phương trình
2
0
1 7 2mx x mm
. Tìm tất cả giá trị của tham số
m
để
phương trình có hai nghiệm
1 2
,
x x
thoả mãn
2 2
1 2
5
x x
.
Câu 5: (3,0 điểm) Trong mặt phẳng
Oxy
, cho ba điểm
1; 1 , 3;1 , 6;0
A B C .
a) Chứng minh rằng ba điểm
, ,
A B C
lập thành một tam giác.
b) Tìm toạ độ điểm
E Oy
sao cho tam giác
ABE
vuông tại
B
.
c) Tính góc 𝐴𝐵𝐶
và chu vi của tam giác
ABC
.
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG TRUNG HỌC PHỔ THÔNG
PHƯỚC KIỂN
ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020
Môn: Toán . Lớp: 10
Thời gian làm bài: 90 phút
(Không k
ể
th
ờ
i gian phát phát đ
ề
)
(ĐỀ CHÍNH THỨC)
Câu 1: (1,0 điểm) Xác định hàm số
2
:
P y x bx c
, biết đồ thị của hàm số
P
đi qua điểm
2;0
A
và có trục đối xứng là
5
x
.
Câu 2: (2,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2
2 4 2
y x x
.
Câu 3: (3,0 điểm) Giải các phương trình sau:
a)
2
3 6 19 4 8
x x x
b)
2
2 7 4 7
x x
c)
7 2 3 3
x x
Câu 4: (1,0 điểm) Cho phương trình
2
0
1 7 2mx x mm
. Tìm tất cả giá trị của tham số
m
để
phương trình có hai nghiệm
1 2
,
x x
thoả mãn
2 2
1 2
5
x x
.
Câu 5: (3,0 điểm) Trong mặt phẳng
Oxy
, cho ba điểm
1; 1 , 3;1 , 6;0
A B C .
a) Chứng minh rằng ba điểm
, ,
A B C
lập thành một tam giác.
b) Tìm toạ độ điểm
E Oy
sao cho tam giác
ABE
vuông tại
B
.
c) Tính góc 𝐴𝐵𝐶
và chu vi của tam giác
ABC
.
--------------HẾT-------------
Sở GD&ĐT TP.HCM ĐÁP ÁN KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020
TRƯỜNG THPT PHƯỚC KIỂN Môn: Toán 10
ĐÁP ÁN Điểm
Câu 1: Xác định hàm số
2
:
P y x bx c
, biết đồ thị của hàm số
P
đi qua điểm
2;0
A
và có trục đối xứng
là
5
x
.
1,0đ
a) Ta có:
2;0 2 4
A P b c
(1)
trục đx:
5 5 10
2
b
x b
a
(2).
Từ (1),(2)
16
c
Vậy .
0,25
0,25
0.25
0.25
Câu 2: Khảo sát sự biến thiên và vẽ đồ thị của
hàm số .
2,0 đ
TXĐ: D=R
Đỉnh I(1;0)
Trục đối xứng x=1
BBT :
x

1
y
0
Nhận xét:
Hàm số đồng biến trên (
1;

)
Hàm số nghịch biến trên (
;1)
x -1 0 1 2 3
y 8 2 0 2 8
Hình vẽ
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0.25
2
10
: 16
P y x x
2
2 4 2
y x x
Câu 3: Giải các phương trình sau : 3,0 đ
a)
2
3 6 19 4 8
x x x
2
2
4 8 0
3 6 19 4 8
x
x x x
2
2
13 58 45 0
x
x x
2
45
1 ( )
13
x
x x l
1
x
0,25
0.5
0,25
b)
2
2 7 4 7
x x
2
4 7 0
2 7 4 7
x
x x
2
4
7
2 7 3 0
x
x x
4
7
1
3
2
x
x x
1
3
2
x x
c)
2
7 2 3 3
7 2 0
3 0
7 2 3 3
x x
x
x
x x
2
3
7
6 3 8 10
x
x x
2
2
3
7
5
2
64 124 8 0
x
x
x x
5
3
2
1
( )
16
2( )
x
x l
x n
0,5
0,5
0,25
0.25
7 2 3 3
x x
0,5
Câu 4 Cho phương trình
. Tìm tất cả giá
trị của tham số để phương trình có hai nghiệm
thoả mãn
1,0 đ
Để phương trình có 2 nghiệm x
1
,x
2
thì
2
1
1 0
49
(7 2 ) 4(1 ).( ) 0
24
m
m
m
m m m
Theo đề ta có :
2 2
1 2
2
1 2 1 2
2
2
2
2 2 2
2
5
2 . 5
2. 5
1
2 7 2 (1 ) 5(1 ) 0
4 28 49 2 2 5 10 5 0
3 16 44 0
2 ( )
22
( )
7
1
3
2
x x
x x x x
m
m
m m m m
m m m m m m
m m
m TM
m TM
m
m
0,25
0,25
0,25
0,25
Câu 5: Trong mặt phẳng , cho ba điểm
.
3,0 đ
2
0
1 7 2mx x mm
m
1 2
,
x x
2 2
1 2
5
x x
Oxy
1; 1 , 3;1 , 6;0
A B C
a. Chứng minh rằng ba điểm lập thành
một tam giác.
.
Ta có nên không cùng phương.
Vậy 3 điểm lập thành một tam giác.
b) Tìm toạ độ điểm
E Oy
sao cho tam giác
ABE
vuông tại
B
.
Do
E Oy
nên
0;
E
E y
.
Ta có
4; 2
BA
,
3; 1
E
BE y
.
Do tam giác vuông tại nên
. 0 3 . 4 2. 1 0
E
BA BE y
7
E
y
.
Vậy
0;7
E .
c) Tính góc 𝐴𝐵𝐶
và chu vi của tam giác
ABC
.
3; 1
BC
𝑐𝑜𝑠𝐴𝐵𝐶
3. 4 1 . 2
. 2
2
10.2 5
.
BC BA
BC BA

𝐴𝐵𝐶
= 120
0
10, 2 5, 5 2
BC AB AC .
Chu vi
10 2 5 5 2
ABC
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0.25
0.25
0.25
0.25
, ,
A B C
4;2 , 7;1
AB AC
4 2
7 1
,
AB AC
 
, ,
A B C
ABE
B
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020 THÀNH PHỐ HỒ CHÍ MINH Môn: Toán . Lớp: 10
TRƯỜNG TRUNG HỌC PHỔ THÔNG
Thời gian làm bài: 90 phút PHƯỚC KIỂN
(Không kể thời gian phát phát đề) (ĐỀ CHÍNH THỨC)
Câu 1: (1,0 điểm) Xác định hàm số P 2
: y  x bx c , biết đồ thị của hàm số P đi qua điểm  A 2  ;  0
và có trục đối xứng là x  5  .
Câu 2: (2,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 2 y  2x  4x  2 .
Câu 3: (3,0 điểm) Giải các phương trình sau: a) 2 3x  6x 19  4x  8 b) 2 2x  7  4  7x c) 7x  2  3  x  3
Câu 4: (1,0 điểm) Cho phương trình 1 m 2
x  7  2m x  m  0 . Tìm tất cả giá trị của tham số m để
phương trình có hai nghiệm x , x thoả mãn 2 2 x  x  5 . 1 2 1 2
Câu 5: (3,0 điểm) Trong mặt phẳng Oxy , cho ba điểm A1;  1 , B 3;  1 , C 6;0 .
a) Chứng minh rằng ba điểm ,
A B, C lập thành một tam giác.
b) Tìm toạ độ điểm E  Oy sao cho tam giác ABE vuông tại B .
c) Tính góc 𝐴𝐵𝐶 và chu vi của tam giác ABC .
--------------HẾT-------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2019 - 2020 THÀNH PHỐ HỒ CHÍ MINH Môn: Toán . Lớp: 10
TRƯỜNG TRUNG HỌC PHỔ THÔNG
Thời gian làm bài: 90 phút PHƯỚC KIỂN
(Không kể thời gian phát phát đề) (ĐỀ CHÍNH THỨC)
Câu 1: (1,0 điểm) Xác định hàm số P 2
: y  x bx c , biết đồ thị của hàm số P đi qua điểm  A 2  ;  0
và có trục đối xứng là x  5  .
Câu 2: (2,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 2 y  2x  4x  2 .
Câu 3: (3,0 điểm) Giải các phương trình sau: a) 2 3x  6x 19  4x  8 b) 2 2x  7  4  7x c) 7x  2  3  x  3
Câu 4: (1,0 điểm) Cho phương trình 1 m 2
x  7  2m x  m  0 . Tìm tất cả giá trị của tham số m để
phương trình có hai nghiệm x , x thoả mãn 2 2 x  x  5 . 1 2 1 2
Câu 5: (3,0 điểm) Trong mặt phẳng Oxy , cho ba điểm A1;  1 , B 3;  1 , C 6;0 .
a) Chứng minh rằng ba điểm ,
A B, C lập thành một tam giác.
b) Tìm toạ độ điểm E  Oy sao cho tam giác ABE vuông tại B .
c) Tính góc 𝐴𝐵𝐶 và chu vi của tam giác ABC .
--------------HẾT------------- Sở GD&ĐT TP.HCM
ĐÁP ÁN KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020
TRƯỜNG THPT PHƯỚC KIỂN Môn: Toán 10 ĐÁP ÁN Điểm
Câu 1: Xác định hàm số P 2
: y  x  bx  c , biết đồ thị của hàm số  1,0đ P đi qua điểm A 2
 ;0 và có trục đối xứng là x  5  . a) Ta có: A 2  ;0P  2  b  c  4 (1) 0,25 b trục đx: x  5     5   b  1  0 (2). 2a 0,25 Từ (1),(2)  c  1  6 0.25 Vậy P 2 : y  x 10x 16 . 0.25
Câu 2: Khảo sát sự biến thiên và vẽ đồ thị của 2,0 đ hàm số 2 y  2x  4x  2 . TXĐ: D=R 0,25 Đỉnh I(1;0) 0,25 Trục đối xứng x=1 0,25 BBT : x  1  y   0,25 0 0,25 Nhận xét:
Hàm số đồng biến trên (1;  )
Hàm số nghịch biến trên (  ;1) x -1 0 1 2 3 0,25 y 8 2 0 2 8 Hình vẽ 0,25 0.25
Câu 3: Giải các phương trình sau : 3,0 đ a) 2 3x  6x 19  4x  8 4x  8  0   3x  6x 19   4x  82 2 0,25     x  2  x 2      45 2 1  3x  58x  45  0 x  1   x   (l)   13  x  1 0.5 0,25 b) 2 2x  7  4  7x  4 4  7x  0 x     7 2 2x  7  4  7x  2 2x  7x  3  0 0,5  4 x    7  1   x  3   x   1  2 x  3  x    2 0,5 c) 7x  2  3  x  3  7x  2  3  x  3   2 7x  2  0   x  3    7  3   x  0   6 3  x  8x 10 7x  2    3 x 32  2   x  3  5 7  x  3  2  5   x    1 2  x   (l)  0,25 16 2 64x 124x  8  0    x  2(n) 0.25  0,5 Câu 4 Cho phương trình 1,0 đ
1m 2x 7 2m x  m  0 . Tìm tất cả giá
trị của tham số m để phương trình có hai nghiệm x , x thoả mãn 2 2 x  x  5 1 2 1 2
Để phương trình có 2 nghiệm x1,x2 thì m  1 1  m0    49 2 (  72 ) m 4(1 ) m .( ) m 0 m  0,25  24 Theo đề ta có : 2 2 x  x  5 1 2 
 x  x 2 2x .x 5 1 2 1 2 2  2m7 m    2.  5    1m  1m   2m 2 2 7 2 ( m 1 ) m 5(1 ) m  0 2 2 2
4m 28m492m2m 5m 10m5  0 2  3  m 1  6m44 0 0,25 m 2 (TM)   22 m  (TM)  3 0,25 0,25
Câu 5: Trong mặt phẳng Oxy , cho ba điểm 3,0 đ A 1  ;  1 , B 3;  1 , C 6;0 .
a. Chứng minh rằng ba điểm , A B, C lập thành một tam giác.  
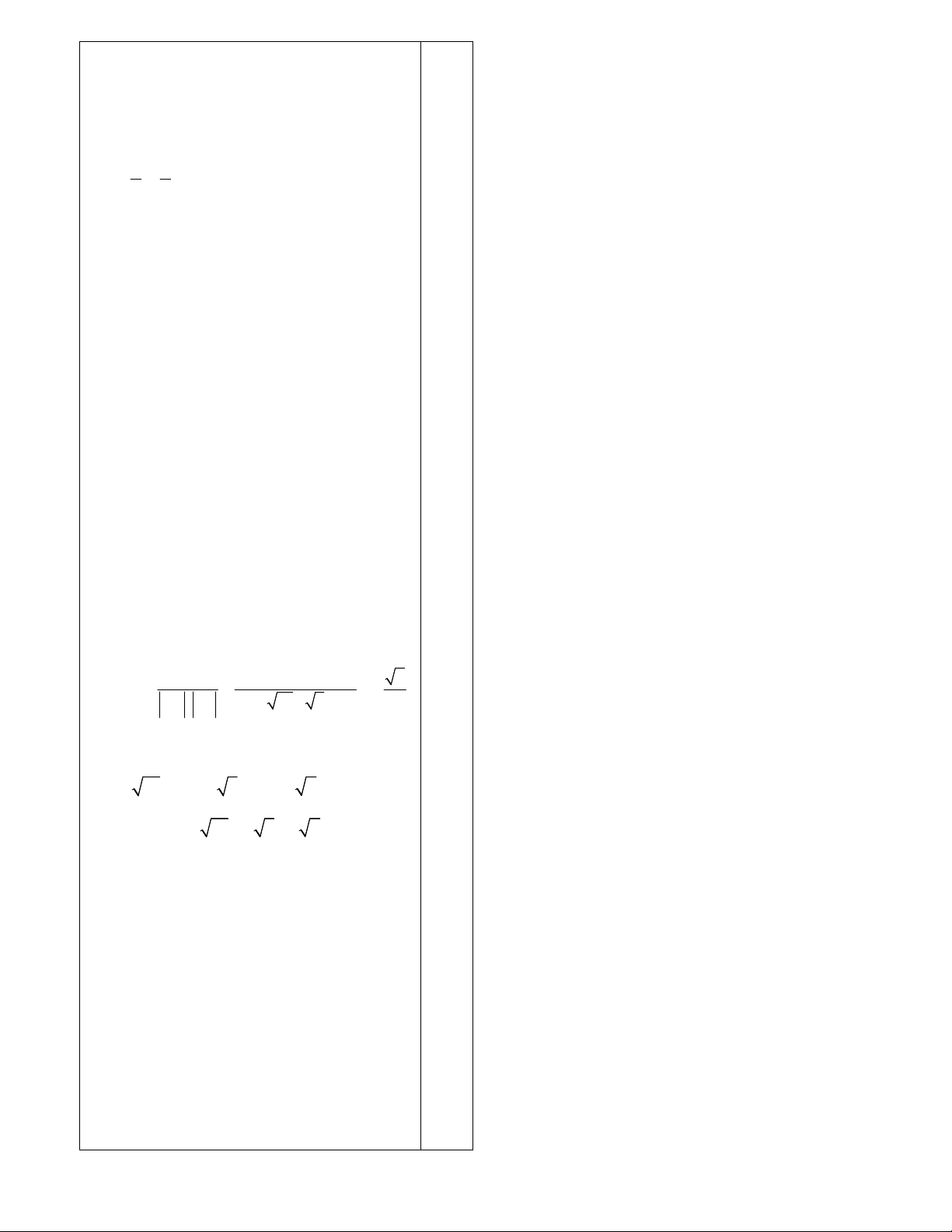
AB  4;2, AC  7;  1 . 0,5 4 2   Ta có
 nên AB, AC không cùng phương. 7 1 Vậy 3 điểm ,
A B,C lập thành một tam giác. 0,25
b) Tìm toạ độ điểm E  Oy sao cho tam giác ABE vuông tại B . 0,25 Do E  Oy nên E 0; y . E    Ta có BA   4  ; 2   , BE   3  ; y   1 . E
Do tam giác ABE vuông tại B nên   B . A BE  0   3  . 4    2. y   1  0 E  y  7 . E Vậy E 0;7 . c) Tính góc 0,25
𝐴𝐵𝐶 và chu vi của tam giác ABC .  BC  3;  1   0,25 BC.BA 3. 4      1 . 2   2
𝑐𝑜𝑠𝐴𝐵𝐶       BC . BA 10.2 5 2 0,25 𝐴𝐵𝐶 = 1200 0,25
BC  10, AB  2 5, AC  5 2 .
Chu vi ABC  10  2 5  5 2 0.25 0.25 0.25 0.25