Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Quốc Trí – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Quốc Trí, thành phố Hồ Chí Minh, đề thi có đáp án và lời giải chi tiết, mời bạn đọc đón xem

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM ĐỀ THI HỌC KÌ I LỚP 10
TRƯỜNG THPT QUỐC TRÍ MÔN THI: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giám thị coi thi không giải thích gì thêm
--------------------------------------------------------------------------------------------------------------------------------
Bài 1. (1 điểm) Tìm tập xác định của hàm số
1
2 2 7
x
y
x x
Bài 2. (3 điểm)
a) Viết phương trình parabol
2
: 0
P y ax bx c a
, biết rằng
P
đi qua điểm
2;1
M và có
đỉnh
1; 1
I
.
Tìm giao điểm của parabol vừa tìm được ở trên với đường thẳng
: 6 5
d y x
.
b) Lập bảng biến thiên và vẽ đồ thị của hàm số
2
2 4
y x x
c) Cho phương trình
2
1 2 2 0
m x mx m
. Tìm
m
để phương trình có hai nghiệm
1 2
,
x x
phân
biệt và
1 2
2 5
x x
.
Bài 3. (3 điểm) Giải các phương trình sau
a)
2 2
3 4 5 4 1 0
x x x x
b)
2
7 10 5
x x x
c)
2
2 3 5 1
x x x
Bài 4. (3 điểm) Trong mặt phẳng
Oxy
cho tam giác
MNP
có
2;1 , 1;3 , 0;4
M N P .
a) Chứng minh tam giác
MNP
là tam giác cân. Tính diện tích và chu vi của tam giác
MNP
.
b) Tìm tọa độ chân đường cao
H
kẻ từ
N
của tam giác
MNP
.
c) Tìm tọa độ hai điểm
,
S R
để
MNRS
là hình vuông, biết điểm
S
có hoành độ dương.
-------------------------------------------- HẾT -------------------------------------------
ĐÁP ÁN ĐỀ THI HỌC KÌ I LỚP 10 NĂM HỌC 2019 – 2020
Bài 1.
Điều kiện xác định
1 0 1
2 0 2
2 7 0 7
2
x x
x x
x
x
Tập xác định
7
1; \ 2;
2
D

Bài 2.
a) Tọa độ đỉnh
1 2
2
b
x b a
a
.
Thay
1
x
vào hàm số ta được
1 2 1 1
a b c a a c a c
. (1)
Thay tọa độ điểm
2;1
M vào hàm số ta được :
4 2 1 4 2.2 1 1
a b c a a c c
(2)
Từ
(1),(2)
suy ra
2 4
a b
.
Phương trình parabol
2
: 2 4 1
P y x x
.
Phương trình hoành độ giao điểm
2 2
1
2 4 1 6 5 2 2 4 0
2
x
x x x x x
x
Với
1 1 1; 1
x y A
.
Với
2 17 2;17
x y B .
b) Tập xác định
D
.
Tọa độ đỉnh
1 5 1; 5
2
b
x y I
a
Trục đối xứng
1
x
.
Bảng biến thiên
Đồ thị :
c)
2
1 2 2 0m x mx m
Điều kiện để phương trình có hai nghiệm phân biệt
1 2
,x x
là
2
1
1
0 1
2
0 12 8 0
4 4 1 2 0
3
m
m
a m
m
m m m
m
Áp dụng định lí Viet ta có
1 2
1 2
2
1
2
1
b m
x x
a m
c m
x x
a m
Theo đề
1 2 1 2 2 2
5 7 2 4
2 5
2 2 1
7 1
m m
x x x x x x
m
m
Và
2 2
1 2 1 2 2 2
2 2
5 5 2
2 5
2 2 1
5 1
m
m
x x x x x x
m
m
Suy ra
2 2
2
2 2
80 98 2
2 2
16
0 0
5 1
49 1 245 1
m m m
m
m
m
m m
2
7
18 98 196 0
14
9
m n
m m
m l
.
Vậy
7
m
thì thỏa mãn yêu cầu bài toán.
Bài 3.
a)
2 2
3 4 5 4 1 0
x x x x
Đặt
2
4 5, 0
t x x t
Phương trình trở thành
2
1
3 4 0
4
t n
t t
t l
Với
2
2
1 4 5 1 2 0 2
t x x x x
(nhận)
b)
2
7 10 5
x x x
2 2
2 2
7 10 5 khi 7 10 0
7 10 5 khi 7 10 0
x x x x x
x x x x x
TH1:
2 2
5
7 10 5 8 15 0
3
x
x x x x x
x
Thử lại nhận nghiệm
5
x
TH2:
2 2
1
7 10 5 6 5 0
5
x
x x x x x
x
Thử lại nhận nghiệm
1
x
Vậy
1;5
S
c)
2
2 3 5 1
x x x
Điều kiện
2
2 3 5 0
x x
2 2 2
3
2 3 5 2 1 6 0
2
x
PT x x x x x x
x
(khi
1
x
)
Thử lại điều kiện nhận hết cả 2 nghiệm.
Vậy
3;2
S .
Bài 4.
a) Ta có
2 2
1 2 3 1 13
MN
2 2
0 2 4 1 13
MP
;
2 2
0 1 4 3 2
NP
Suy ra tam giác MNP cân tại
M
(vì
MN MP
)
2 2 13 2
MNP
p MN MP NP
3;2 ; 2; 3
MN MP
 
Suy ra
1 2 2 1
1 5
2 2
MNP
S a b a b
b) Gọi
0 0
;
H x y
là tọa độ chân đường cao kẻ từ N của tam giác
MNP
.
Khi đó
0 0
0 0
0
0 0
0
2 3 11 0
2 1 3 3 0
2 2
2; 1 2;3
1 3
x y
NH MP
x y
x k
x y k
MH kMP
y k
12 2 49
2 2 2 3 3 1 11 0 13 12 ;
13 13 13
k k k k H
.
c)
MNRS
là hình vuông
Gọi
, ; ;
R R S S
R x y S x y
là tọa độ các điểm thỏa yêu cầu bài toán
Khi đó
3 3
2 2
R S R S
R S R S
x x x x
MN SR
y y y y
……
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM
ĐỀ THI HỌC KÌ I LỚP 10 TRƯỜNG THPT QUỐC TRÍ MÔN THI: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giám thị coi thi không giải thích gì thêm
-------------------------------------------------------------------------------------------------------------------------------- x  1
Bài 1. (1 điểm) Tìm tập xác định của hàm số y   x  22x  7 Bài 2. (3 điểm)
a) Viết phương trình parabol P  2
: y  ax  bx  c a  0, biết rằng P  đi qua điểm M 2;1 và có đỉnh I 1; 1  .
Tìm giao điểm của parabol vừa tìm được ở trên với đường thẳng d  : y  6  x  5.
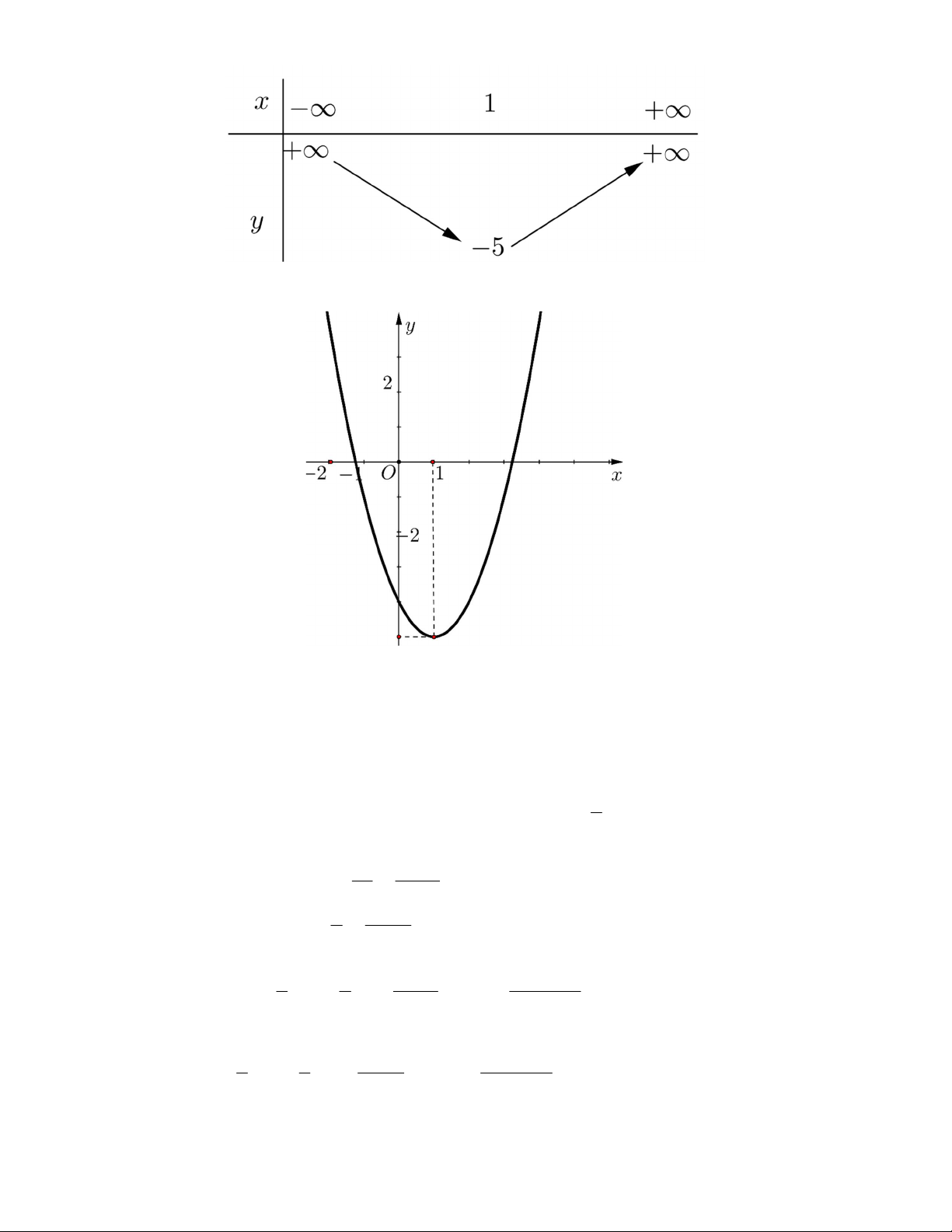
b) Lập bảng biến thiên và vẽ đồ thị của hàm số 2 y  x  2x  4
c) Cho phương trình m   2
1 x  2mx  m  2  0 . Tìm m để phương trình có hai nghiệm x ,x phân 1 2 biệt và 2x  5x . 1 2
Bài 3. (3 điểm) Giải các phương trình sau a) 2 2
3 x  4x  5  x  4x  1  0 b) 2 x  7x  10  x  5 c) 2 2x  3x  5  x  1
Bài 4. (3 điểm) Trong mặt phẳng Oxy cho tam giác MNP có M 2;1,N 1;3,P 0;4 .
a) Chứng minh tam giác MNP là tam giác cân. Tính diện tích và chu vi của tam giác MNP .
b) Tìm tọa độ chân đường cao H kẻ từ N của tam giác MNP .
c) Tìm tọa độ hai điểm S,R để MNRS là hình vuông, biết điểm S có hoành độ dương.
-------------------------------------------- HẾT -------------------------------------------
ĐÁP ÁN ĐỀ THI HỌC KÌ I LỚP 10 NĂM HỌC 2019 – 2020 Bài 1.  x   1  0 x   1   Điều kiện xác định x   2  0  x   2 2  x 7 0    7  x    2  
Tập xác định D    7 1; \ 2  ; 2    Bài 2. b  a) Tọa độ đỉnh x   1  b  2a . 2a
Thay x  1 vào hàm số ta được a  b  c  1   a  2a  c  1   a   c  1  . (1)
Thay tọa độ điểm M 2;1 vào hàm số ta được :
4a  2b  c  1  4a  2.2a  c  1  c  1 (2)
Từ (1),(2) suy ra a  2  b  4  .
Phương trình parabol P  2 : y  2x  4x  1.
Phương trình hoành độ giao điểm x   1 2 2 2x  4x  1  6
 x  5  2x  2x  4  0  x    2 
Với x  1  y  1  A1;   1 .
Với x  2  y  17  B  2  ;17 .
b) Tập xác định D   . b  Tọa độ đỉnh x 
 1  y  5  I 1;5 2a Trục đối xứng x  1. Bảng biến thiên Đồ thị : c) m   2 1 x  2mx  m  2  0
Điều kiện để phương trình có hai nghiệm phân biệt x ,x là 1 2     m    1 a 0 m  1 m   1        2    4m  4  m 1m  2  2 0  0 1  2m  8  0  m   3  b  2m x  x    1 2
Áp dụng định lí Viet ta có a m  1  c m  2 x  x   1 2  a m  1 5 7 2m 4m
Theo đề 2x  5x  x  x  x   x  1 2 1 2 2 2 2 2 m  1 7 m  1 5 5 m 2 2 m   2 2 2  
Và 2x  5x  x  x  x   x  1 2 1 2 2 2 2 2 m  1 5m   1 16m 2m  2 2 80m  98 2 2 m  m  2 Suy ra     49m 1 0 0 2 5m   1 245m  12 m   7 n 2 18m 98m 196 0         14 . m   l  9
Vậy m  7 thì thỏa mãn yêu cầu bài toán. Bài 3. a) 2 2
3 x  4x  5  x  4x  1  0 Đặt 2
t  x  4x  5,t  0 Phương trình trở thành t  1 n 2   t  3t  4  0   t  4   l
Với t   x  x    x  2 2 1 4 5 1 2  0  x  2 (nhận) b) 2 x  7x  10  x  5 2 2 x
  7x  10  x  5 khi x  7x  10  0   2 2  x
  7x  10  x  5 khi x  7x  10  0  x   5 TH1: 2 2
x  7x  10  x  5  x  8x  15  0  x   3 
Thử lại nhận nghiệm x  5 x   1 TH2: 2 2 x
  7x  10  x  5  x
  6x  5  0  x   5 
Thử lại nhận nghiệm x  1 Vậy S  1;  5 c) 2 2x  3x  5  x  1 Điều kiện 2 2x  3x  5  0 x   3 2 2 2
PT  2x  3x  5  x  2x  1  x  x  6  0   x  (khi x  1)   2 
Thử lại điều kiện nhận hết cả 2 nghiệm. Vậy S  3;  2 . Bài 4. 2 2
a) Ta có MN  1  2  3   1  13
MP    2    2 0 2 4 1  13 2 2 ; NP  0   1  4  3  2
Suy ra tam giác MNP cân tại M (vì MN  MP ) 2p
 MN  MP  NP  2 13  2 MNP  
MN  3;2; MP  2;3 1 5 Suy ra S  a b  a b  MNP 1 2 2 1 2 2
b) Gọi H x ;y là tọa độ chân đường cao kẻ từ N của tam giác MNP . 0 0   N  H  MP   2x  3y  11  0 2 x  1  3 y  3  0  0   0  0 0 Khi đó         MH   kMP   x k  x  2;y   1  k 2;3 2 2 0 0 0 y   1  3k  0      k     k   12 2 49 2 2 2 3 3
1  11  0  13k  12  k   H  ; . 13 13 13    c) MNRS là hình vuông
Gọi R x ,y ;S x ;y là tọa độ các điểm thỏa yêu cầu bài toán R R S S    x   x  3 x   x  3 Khi đó R S R S MN  SR    y y 2 y     y    2 R S  R S ……