Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Trần Khai Nguyên – TP HCM

SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKI, KHỐI 10, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN
Thời gian : 90 phút (không kể thời gian giao đề)
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 101 x 16  x 
Câu 1: [1 điểm] Xét tính chẵn, lẻ của hàm số y  f  x  . 4 2 x  5x  4
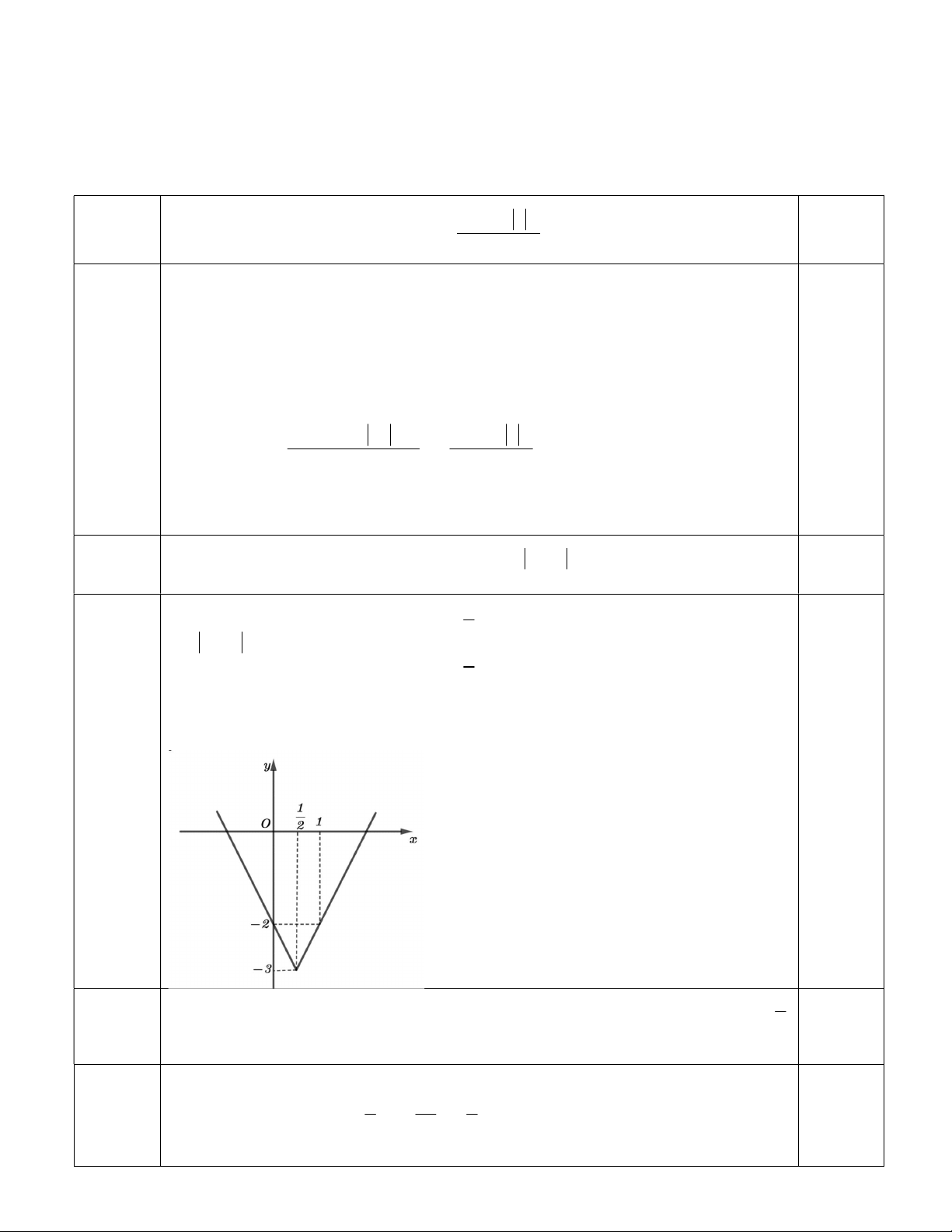
Câu 2: [1 điểm] Vẽ đồ thị hàm số y  2x 1  3 . 4
Câu 3: [1 điểm] Viết phương trình của parabol 2
(P) : y  ax  bx  3 biết (P) có trục đối xứng là x   3 và đi qua điểm M  2  ;  1 . 2 x  4x 1
Câu 4: [1 điểm] Gọi x là nghiệm nguyên dương của phương trình
 x  3 . Hãy tính giá trị của 0 x  3 biểu thức 2 A  2x  2019 1. 0
Câu 5: [1 điểm] Giải và biện luận phương trình 2(m 1)x  m(x 1)  2m  3 .  3  2 y  2  5  
Câu 6: [1 điểm] Giải hệ phương trình x 1  . 2   5 y  2  3  x 1
Câu 7: [1 điểm] Tìm giá trị của tham số m để phương trình 2
x  2x  2m  2x 1 có 2 nghiệm phân biệt. 
Câu 8: [2 điểm] Trong mặt phẳng Oxy cho A 2
 ; 6 , B4; 4, AC  4;4.  
a) Xác định tọa độ điểm C và tìm tọa độ điểm D thoả AD  CB .
b) Chứng minh rằng tứ giác ADBC là hình chữ nhật. Tìm tọa độ tâm và bán kính đường tròn ngoại tiếp tam giác ADB .   
Câu 9: [1 điểm] Cho tam giác ABC có AB  5, BC  7,CA  8 . Tính A . B AC và góc BAC . HẾT
Mã đề : 101 - Môn : TOÁN.
SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKI, KHỐI 10, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN
Thời gian : 90 phút (không kể thời gian giao đề)
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 102 x  x  25
Câu 1: [1 điểm] Xét tính chẵn, lẻ của hàm số y  f  x  . 4 2 x 10x  9
Câu 2: [1 điểm] Vẽ đồ thị hàm số y  1 2x  3 . 5
Câu 3: [1 điểm] Viết phương trình của parabol 2
(P) : y  ax  bx  3 biết (P) có hoành độ đỉnh bằng 4
và đi qua điểm M 2;  1 . 2 4x  x
Câu 4: [1 điểm] Gọi x là nghiệm nguyên dương của phương trình
 4  x . Hãy tính giá trị của 0 4  x biểu thức 2 A  2019  3x 1. 0
Câu 5: [1 điểm] Giải và biện luận phương trình 2 2
(m 1)(x  2)  2m  m 1.  4 3 y 1  10  
Câu 6: [1 điểm] Giải hệ phương trình x 2  . 3   y 1  1  x  2
Câu 7: [1 điểm] Tìm giá trị của tham số m để phương trình 2
x 1 2m  2x 1 có 2 nghiệm phân biệt. 
Câu 8: [2 điểm] Trong mặt phẳng Oxy cho B  2
 ; 6 , C4; 4 , CA   2  ; 2 .  
a) Xác định tọa độ điểm A và tìm tọa độ điểm D thoả CD  AB .
b) Chứng minh rằng tứ giác ABDC là hình chữ nhật. Tìm tọa độ tâm và bán kính đường tròn ngoại tiếp tam giác BDC .   
Câu 9: [1 điểm] Cho tam giác ABC có AB  4 5, BC  5 2,CA  3 10 . Tính A . B AC và góc BAC . HẾT
Mã đề : 101 - Môn : TOÁN.
SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKI, KHỐI 10, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN
Thời gian : 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN CHẤM TOÁN 10_ĐỀ 101 Câu 1 x 16  x  Điểm chi [A]
Xét tính chẵn, lẻ của hàm số y  f x  4 2 tiết x  5x  4 (1 điểm) Hàm số có nghĩa 4 2  x  5x  4  0   x  1  2 x   1  2 x  4  0   x  2  Suy ra TXĐ: D   \ 1  ;  2 . Ta có x   D  x  . D 0,25 x16  x  x16  x  0,25 Xét f x      f x . 4 2 4 2  
x 5x  4 x  5x  4 0,25 0,25
Vậy f  x là hàm lẻ Câu 2[A]
Vẽ đồ thị hàm số: y  2x 1  3 Điểm chi tiết (1 điểm)  1 2x  4, khi x   2
y  2x 1  3  y   1  2  x  2, khi x   2 0,25 Bảng giá trị x 0 1/2 1 y -2 -3 -2 0,25 0,25 0,25 Câu 3 4
Viết phương trình của parabol 2
(P) : y  ax  bx  3 biết (P) có trục đối xứng là x   Điểm chi [A] 3 tiết và đi qua điểm M  2  ;  1 . 2
(1 điểm) (P) : y  ax  bx  3 4 b 4
(P) có trục đối xứng x        8a  3b  0 0,25 3 2a 3 (P) đi qua điểm M  2  ;  1  4a  2b  4
Mã đề : 101 - Môn : TOÁN. 8  a  3b  0 a  3  0,25   Giải hệ:  4a  2b  4 b   8  0,25 Vậy 2 (P) : y  3  x  8x  3 0,25 2 Câu 4[A] x  4x 1
Gọi x là nghiệm nguyên dương của phương trình  x  3 . Điểm 0 x  3 chi tiết
Hãy tính giá trị của biểu thức 2 A  2x  2019 1. 0
(1 điểm) Điều kiện x  3 0,25 x  4 (n) pt 2 2
 x  4x 1  x  3  x  5x  4  0   0,25 x  1 (l) Vậy x  4 0,25 0 Khi đó: 2
A  2.4  2019 1  1988 0,25 Câu
Giải và biện luận phương trình 2(m 1)x  m(x 1)  2m  3 . Điểm 5[A] chi tiết
(1 điểm) pt  x(2m  2  m)  m  3  (m  2)x  m  3 0,25
Trường hợp 1: m  2  0  m  2 m  3 0,25
Phương trình có nghiệm duy nhất x  m  2
Trường hợp 2: m  2  0  m  2
Ta có: 0.x  1 ( pt vô nghiệm) Kết luận: 0,25  m  3 0,25 m  2  S    m  2 m  2 S   Câu 6  3 Điểm  2 y  2  5   chi tiết
Giải hệ phương trình x 1  2   5 y  2  3  x 1 (1 điểm) x  1 Điều kiện:   y  2  0,25  1 a   Đặt x 1  b   y  2  b  0 Ta có hệ phương trình 3  a  2b  5 0,25  2a  5b  3 a  1   b   1  nhan 0,25 1 Với a  1 , ta có
 1  x 1  1  x  2 x 1
Với b  1, ta có y  2 1  y  2 1  y  1  0,25
So với điều kiện, hệ phương trình đã cho có nghiệm 2;  1 . Câu 7
Tìm giá trị của tham số m để phương trình 2
x  2x  2m  2x 1 có 2 nghiệm phân Điểm
Mã đề : 101 - Môn : TOÁN. [A] biệt. chi tiết
(1 điểm) Lời giải chi tiết 2x 1  0  1 x   2 
x  2x  2m  2x 1     2 . x  2x  2m   2x  2 2 1 2 3  x  2x 1 2m  0  * 0,25 1
Đặt t  x  ; phương trình (*) trở thành: 2 2  1   1  3 t   2 t  1 2m  0      2   2  3 2
 3t  t   2m  0 ** 4 0,25
Yêu cầu bài toán thỏa mãn khi phương trình (*) có hai nghiệm phân biệt x , x thỏa mãn 1 2 1
  x  x khi và chỉ khi phương trình (**) có hai nghiệm phân biệt t ,t thỏa 1 2 2 1 2     2  3  1  4.3.  2m  0     4    1
0  t  t . Điều kiện: S    0 1 2 3   3 0,25  2m  4 P   0  3  1 m   3  1 3    m  . 3  3 8 m   8 0,25 
Câu 8[A] Trong mặt phẳng Oxy cho A 2
 ; 6 , B4; 4 , AC  4;4 .   Điểm
a) Xác định tọa độ điểm C và tìm tọa độ điểm D thoả AD  CB . chi tiết
b) Chứng minh rằng tứ giác ADBC là hình chữ nhật. Tìm tọa độ tâm và bán kính
đường tròn ngoại tiếp tam giác ADB .  x  2  4 x  2
a) Gọi Cx ; y AC  x  2; y  6 C C      C 2; 2  C C   C C  (1 điểm) y  6  4 y  2  C  C 0,25 0,25 Gọi Dx ; y D D   
Mà AD  x  2; y  6 , CB  2; 2   D D  0,25   x  2  2 x  0 D D AD  CB      D0; 8   0,25 y  6  2  y  8   D  D   
b) AB  6;2 , AC  4;4 , CB  2; 2  
Mã đề : 101 - Môn : TOÁN. 6 2   Ta có: 
 AB & AC không cùng phương. 4 4
 A, B, C không thẳng hàng
 A, B, C là 3 đỉnh của một tam giác  
AD  CB  Tứ giác ADBC là hình bình hành. 0,25  
Có AC.CB  4.2  4.(2)  0    AC  CB  AC  CB  ABC vuông tại C 0,25
Vậy tứ giác ADBC là hình chữ nhật.  2 2
AB  AB  6  2  2 10 0,25
Đường tròn ngoại tiếp tam giác ADB có đường kính AB, tâm I trung điểm của đoạn thẳng AB.  x  x A B x   I  AB Ta có 2 
 I1;5 , bán kính R   10 0,25 y  y  2 A B y  I  2   
Câu 9[A] Cho tam giác ABC có AB  5, BC  7,CA  8 . Tính A . B AC và góc BAC . Điểm chi tiết
(1 điểm) + Xét tam giác ABC , ta có  2   2 2   2
BC  (AC  AB)  AC  AB  2AC.AB  
2 2 2 1 AB.AC   AC AB BC      2      0,25  AB.AC  20 + Ta có:     AB.AC 1 0,25
cos A  cos(AB;AC)     AB . AC 2 0,25 0,25 Vậy góc 0 BAC  60
Mã đề : 101 - Môn : TOÁN.