Đề thi học kỳ 1 Toán 10 năm học 2018 – 2019 trường Lương Thế Vinh – Hà Nội

Đề thi học kỳ 1 Toán 10 năm học 2018 – 2019 trường Lương Thế Vinh – Hà Nội mã đề 132 gồm 5 trang, đề được biên soạn theo hình thức trắc nghiệm khách quan hoàn toàn, học sinh làm bài trong 90 phút, mời các bạn đón xem

77 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/5 - Mã đề thi 132
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT LƯƠNG THẾ VINH
ĐỀ THI HỌC KỲ I – NĂM HỌC
2018 – 2019
Môn: TOÁN 10
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm)
Mã đề thi
132
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Câu 1: Gọi
1 2
,m m
là hai giá trị khác nhau của
m
để phương trình
2 2
3 3 4 0
x x m m
có hai
nghiệm phân biệt
1 2
,x x
sao cho
1 2
2x x
. Tính
1 2 1 2
m m m m
.
A.
. B.
3
. C.
5
. D.
.
Câu 2: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?
a) Số 2 là số nguyên tố.
b) Số
2018
3 1
chia hết cho 2.
c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của hình
bình hành đó.
d) Mọi hình chữ nhật luôn có chiều dài lớn hơn chiều rộng.
e) Một số chia hết cho 28 thì chia hết cho 8.
A.
3
. B.
1
. C.
. D.
.
Câu 3: Gọi
0
m
là giá trị của tham số
m
để phương trình
2 1 0
m x x
vô nghiệm. Khẳng định
nào sau đây là đúng?
A.
0
m
. B.
0
2;0
m
. C.
0
0;1
m
. D.
0
1;1
m
.
Câu 4: Cho hình vuông
ABCD
tâm
O
. Đẳng thức nào sau đây là sai?
A.
DA OC OB
. B.
AO DO CD
. C.
AB DC
. D.
BO DO AC
.
Câu 5: Đồ thị nào sau đây là đồ thị của hàm số
2
2 3y x x
:
Hình
1
x
y
O
1
Hình
2
x
y
O
1
Hình
3
x
y
O
1
Hình
4
x
y
O
1
A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Câu 6: Cho
ABC
có
9
AB
,
8
BC
,
0
B 60
. Tính độ dài
AC
.
A.
73
. B.
217
. C.
8
. D.
113
.
Câu 7: Cho hàm số
2
4 1y x x
. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số nghịch biến trên khoảng
;3

. B. Hàm số đồng biến trên khoảng
3;

.
C. Hàm số có giá trị nhỏ nhất là
3
. D. Đồ thị hàm số đi qua điểm
0;1
A
.
Trang 2/5 - Mã đề thi 132
Câu 8: Cho hàm số
2
3 2 khi 1 2
4 khi 2
x x
f x
x x
. Tính giá trị
3f
.
A. Không xác định. B.
3 5
f hoặc
3 3
f
.
C.
3 5
f . D.
3 3
f
.
Câu 9: Tính tổng bình phương các nghiệm của phương trình
2
2 13 0
x x
.
A.
22
. B.
. C.
30
. D.
28
.
Câu 10: Gọi
0
m
là giá trị của
m
để hệ phương trình
3
2
9
x y m
mx y m
có vô số nghiệm. Khi đó:
A.
0
1
1;
2
m
. B.
0
1
0;
2
m
. C.
0
1
;2
2
m
. D.
0
1
;0
2
m
.
Câu 11: Hệ phương trình
3
3
2019
2019
x y x
y x y
có số nghiệm là:
A.
. B.
. C.
1
. D.
3
.
Câu 12: Số nghiệm của phương trình
2
1 2
x x
là:
A.
. B.
. C.
3
. D.
1
.
Câu 13: Tập xác định của hàm số
1
1
4
y x
x
là:
A.
1;4
. B.
1;4
. C.
1;4
. D.
1;4
.
Câu 14: Cho
ABC
có
1;2
A
,
0;3
B
,
5; 2
C
. Tìm tọa độ chân đường cao hạ từ đỉnh
A
của
ABC
.
A.
0;3
. B.
0; 3
. C.
3;0
. D.
3;0
.
Câu 15: Cho các đường thẳng sau.
1
3
: 2
3
d y x
2
1
: 1
3
d y x
3
3
: 1 2
3
d y x
4
3
: 1
3
d y x
Khẳng định nào đúng trong các khẳng định sau?
A.
2
d
,
3 4
,d d
song song với nhau. B.
2
d
và
4
d
song song với nhau.
C.
1
d
và
4
d
vuông góc với nhau. D.
2
d
và
3
d
song song với nhau.
Câu 16: Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là:
A.
1
. B.
. C.
3
. D.
.
Câu 17: Có bao nhiêu giá trị nguyên của
m
để đường thẳng
3y mx
không có điểm chung với
Parabol
2
1
y x
?
A.
. B.
9
. C.
. D.
8
.
Câu 18: Tìm tất cả các giá trị của tham số
m
để phương trình
2
0
3
x m x m
x
có nghiệm.
A.
; 1
m

. B.
1;m

. C.
1;m

. D.
m R
.
Câu 19: Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số
2
2 2
y x x
xác định trên R. B. Hàm số
3
y x
là hàm số lẻ.
C. Hàm số
2
1
y x
là hàm số chẵn. D. Hàm số
2
1
y x
là hàm số chẵn.
Trang 3/5 - Mã đề thi 132
Câu 20: Phương trình
3 2 5
x x
có hai nghiệm
1 2
,x x
. Tính
1 2
x x
.
A.
14
3
. B.
28
3
. C.
7
3
. D.
14
3
.
Câu 21: Cho
3;4
A
,
2;1
B
,
0;5
C
. Tính độ dài trung tuyến
AM
của
ABC
.
A.
13
. B.
5
. C.
. D.
17
.
Câu 22: Số giá trị nguyên của
m
để phương trình
2
4 1
x m
có bốn nghiệm phân biệt là:
A.
. B.
. C.
3
. D.
5
.
Câu 23: Cho
ABC
vuông cân tại
A
,
AB a
. Tính độ dài vectơ
4
AB AC
.
A.
20a
. B.
5a
. C.
17a
. D.
17a
.
Câu 24: Cho phương trình
1 5 3. 1 5
x x x x m
. Có tất cả bao nhiêu giá trị nguyên của
tham số m để phương trình trên có nghiệm?
A.
. B.
8
. C.
. D. vô số.
Câu 25: Biết phương trình
4 2 2
3 1 0
x mx m
có bốn nghiệm phân biệt
1 2 3 4
, , ,x x x x
. Tính
1 2 3 4 1 2 3 4
. . .M x x x x x x x x
được kết quả là:
A.
2
1
M m
. B.
3M m
. C.
3M m
. D.
2
1
M m
.
Câu 26: Tìm
,a b
để đồ thị hàm số
y ax b
đi qua hai điểm
1; 2
A
,
3;5
B
.
A.
7 1
;
4 4
a b
. B.
7 1
;
4 4
a b
. C.
1 7
;
4 4
a b
. D.
1 4
;
7 7
a b
.
Câu 27: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2m m x mx x m
nghiệm
đúng với
x R
.
A.
2
m
. B.
2
m
. C.
1
m
. D.
1
m
.
Câu 28: Biết phương trình
2
1 3 3 1
x x x
có hai nghiệm
1 2
,x x
. Tính giá trị biểu thức
1 2
1 . 1
x x
.
A.
1
. B.
. C.
2
. D.
3
.
Câu 29: Xác định hàm số
2
y ax bx c
biết đồ thị của hàm số đó cắt trục tung tại điểm có tung độ là
3
và giá trị nhỏ nhất của hàm số là
25
8
tại
1
4
x
.
A.
2
2 3y x x
. B.
2
1
3
2
y x x
. C.
2
2 3y x x
. D.
2
2 3y x x
.
Câu 30: Cho các tập hợp :
A
{cam, táo, mít, dừa}
B
{táo, cam}
C
{dừa, ổi, cam, táo, xoài}
Tập
\
A B C
là :
A. {táo, cam}. B. {mít}. C. {mít, dừa}. D. {dừa}.
Câu 31: Hệ phương trình
2
1
2 2 2 0
x y
x x y
có số nghiệm là:
A.
1
. B.
. C.
. D.
.
Câu 32: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 4 0
x m x m
có hai nghiệm
phân biệt.
A.
6
m
. B.
6
m
. C.
6
m
. D.
m
.
Trang 4/5 - Mã đề thi 132
Câu 33: Hệ phương trình
2
2 2
2
2 9
x xy
x xy y
có nghiệm là
0 0
;x y
thỏa mãn
0
1
x
. Tính
0 0
x y
:
A.
. B.
5
. C.
1
. D.
3
.
Câu 34: Cho
4
a b
,
2
a
,
3
b
. Tính
a b
.
A.
3
. B.
10
. C.
12
. D.
.
Câu 35: Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa. Biết rằng
mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là: có 4 bạn thích cả ba môn; có 9 bạn thích Văn
và Sử; có 5 bạn thích Sử và Địa; có 11 bạn thích Văn và Địa; có 24 bạn thích Văn; có 19 bạn thích Sử và
có 22 bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa?
A.
21
. B.
23
. C.
24
. D.
22
.
Câu 36: Cho
1;4
M
,
1;3
N
,
0;6
P
. Gọi
;Q a b
là điểm thỏa mãn
NPMQ
là hình bình hành.
Tổng
a b
bằng:
A.
1
. B.
. C.
. D.
1
.
Câu 37: Cho
ABC
có
5
AB
,
0
A 40
,
0
B 60
. Độ dài
BC
gần nhất với kết quả nào?
A.
3,7
. B.
3,3
. C.
3,5
. D.
3,1
.
Câu 38: Cho
ABC
đều ,
6
AB
và
M
là trung điểm của
BC
.Tích vô hướng
.AB MA
bằng:
A.
18
. B.
27
. C.
18
. D.
27
.
Câu 39: Cho
0;3
A
,
4;0
B
,
2; 5
C
. Tính
.AB BC
.
A.
16
. B.
9
. C.
10
. D.
9
.
Câu 40: Cho hai vectơ
,a b
khác vectơ
thỏa mãn
1
. .
2
a b a b
. Khi đó góc giữa hai vectơ
,a b
là:
A.
0
60
. B.
0
120
. C.
0
150
. D.
0
30
.
Câu 41: Tìm tất cả các giá trị của tham số
m
để hàm số
1 . 2y m x m
đồng biến trên
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 42: Cho tam giác đều ABC, gọi D là điểm thỏa mãn
2
DC BD
. Gọi R và r lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số
R
r
.
A.
5
2
. B.
5 7 7
9
. C.
7 5 5
9
. D.
7 5 7
9
.
Câu 43: Phương trình
2
2 1 2 1 2
x x x x x
có số nghiệm là:
A.
1
. B.
3
. C.
. D.
.
Câu 44: Cho
ABC
có
2AB
,
3
AC
,
0
A 60
. Tính độ dài đường phân giác trong góc A của tam
giác ABC
A.
12
5
. B.
6 2
5
. C.
6 3
5
. D.
6
5
.
Câu 45: Tính diện tích
ABC
biết
3, 5, 6
AB BC CA
.
A.
56
. B.
48
. C.
. D.
8
.
Câu 46: Cho
ABC
có
3, 5
AB BC
và độ dài trung tuyến
13
BM . Tính độ dài
AC
.
A.
11
. B.
. C.
9
2
. D.
10
.
Câu 47: Cho
ABC
vuông ở
A
, biết
0
30
C
,
3
AB
. Tính độ dài trung tuyến
AM
.
A.
3
. B.
. C.
5
2
. D.
7
2
.
Trang 5/5 - Mã đề thi 132
Câu 48: Tìm tất cả các giá trị của tham số
m
để phương trình
2 2
1 1 3 0
m x m x
có hai nghiệm
trái dấu.
A.
1
m
. B.
0
m
. C.
0
m
. D.
1
m
.
Câu 49: Cho hàm số
2
2 8 khi 2
2 12 khi 2
x x x
y
x x
. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số khi
1;4
x
. Tính
M m
.
A.
14
. B.
13
. C.
4
. D.
9
.
Câu 50: Biết hệ phương trình
2 4
2 3
y x xy
y x xy
có nghiệm
0 0
;x y
với
0
0
x
. Tỉ số
0
0
y
x
bằng:
A.
. B.
1
2
. C.
1
. D.
1
.
-----------------------------------------------
----------- HẾT ----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/21
ĐÁP ÁN THAM KHẢO
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
A
C
B A
A
B C
C
B
D
A
A
A
B A
C
B C
D
D
C
D
C
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B C
B A
D
A
C
D
B
D
D
A
D
D
A
C
D
D
C
A
B A
A
B A
HƯỚNG DẪN GIẢI
Câu 1. [0D1.1-2] Gọi
1
m
,
2
m
là hai giá trị khác nhau của
m
để phương trình
2 2
3 3 4 0
x x m m
có hai nghiệm phân biệt
1
x
,
2
x
sao cho
1 2
2
x x
. Tính
1 2 1 2
m m m m
.
A.
4
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn C.
Phương trình có hai nghiệm phân biệt
2
4 12 7 0
m m
.
Khi đó phương trình có hai nghiệm phân biệt
1
x
,
2
x
. Theo Vi-et ta có:
1 2
2
1 2
3
. 3 4
x x
x x m m
.
Mà
1 2
2
x x
nên ta có:
2 2 2
2 2
2
2
2 3 1
2 3 4
3 2 0
x x x
x m m m m
1
2
m
m
.
Vậy
1 2 1 2
5
m m m m
.
Câu 2. [0D3.2-2] Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?
a) Số 2 là số nguyên tố.
b) Số
2018
3 1
chia hết cho 2.
c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo
của hình bình hành đó.
d) Mọi hình chữ nhật luôn có chiều dài lớn hơn chiều rộng.
e) Một số chia hết cho 28 thì chia hết cho 8.
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn A.
Các mệnh đề đúng là a; b.
Chú ý: d) sai vì hình vuông cũng là hình chữ nhật.
Câu 3. [0D3.2-2] Gọi
0
m
là giá trị của tham số
m
để phương trình
2 1 0
m x x
vô nghiệm.
Khẳng định nào sau đây là đúng?
A.
0
m
. B.
0
2;0
m . C.
0
0;1
m . D.
0
1;1
m .
Lời giải
Chọn B.
Ta có:
2 1 0
m x x
1 1 0
m x
. Phương trình vô nghiệm
1
m
.
Câu 4. [0H1-2-1] Cho hình vuông
ABCD
tâm
O
. Đẳng thức nào sau đây là sai?
A.
DA OC OB
. B.
AO DO CD
. C.
AB DC
. D.
BO DO AC
.
Lời giải
Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/21
Ta có
AO DO
OC DO
DC CD
.
Câu 5. [0D2-3-1] Đồ thị nào sau đây là đồ thị của hàm số
2
2 3
y x x
?
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Lời giải
Chọn A.
Đồ thị của hàm số
2
2 3
y x x
có hệ số
1 0
a
nên bề lõm hướng lên trên
loại hình 2.
Đồ thị của hàm số
2
2 3
y x x
còn có trục đối xứng
1
x
, cắt trục tung tại điểm có tọa độ
0;3
, cắt trục hoành tại các điểm
3;0
,
1;0
do đó ta chọn hình 4.
Câu 6. [0H2-3-2] Cho tam giác
ABC
có
9
AB
,
8
BC
,
60
B
. Tính độ dài
AC
.
A.
73
. B.
217
. C.
8
. D.
113
.
Lời giải
Chọn A.
Áp dụng định lí côsin cho tam giác
ABC
ta có
2 2
2 . .cos
AC AB BC AB BC B
2 2
8 9 2.8.9.cos60 73
.
Câu 7. [0D2.3-1] Cho hàm số
2
4 1
y x x
. Chọn khẳng định đúng trong các khẳng định sau::
A. Hàm số nghịch biến trên khoảng
;3
 . B. Hàm số đồng biến trên khoảng
3;

.
C. Hàm số có giá trị nhỏ nhất là
3
. D. Đồ thị hàm số đi qua điểm
0;1
A .
Lời giải
Chọn B.
Đỉnh
2; 5
I
.
Vì
1 0
a
, nên hàm số có bảng biến thiên:
x

2
y
5
x
y
O
3
4
1
2
x
y
O
1
3
4
1
x
y
O
1
4
3
1
x
y
O
1
3
4
3
1
A
B
C
D
O
C
A
B
9
8
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/21
Hàm số đồng biến trên
2;

.
Do đó hàm số đồng biến trên
3;

.
Câu 8. [0D2.1-1] Hàm số
2
3 2 khi 1 2
4 khi 2
x x
f x
x x
. Tính giá trị
3
f
.
A. Không xác định. B.
3 5
f hoặc
3 3
f
.
C.
3 5
f . D.
3 3
f
.
Lời giải
Chọn C.
Ta có:
2
3 3 4 5
f .
Câu 9. [0D3.2-1] Tính tổng bình phương các nghiệm của phương trình
2
2 13 0
x x
.
A.
22
. B.
4
. C.
30
. D.
28
.
Lời giải
Chọn C.
Ta có:
. 13 0
a c
phương trình có hai nghiệm trái dấu.
Theo Vi-et ta có:
1 2 1 2
2; 13
x x x x
.
Vậy
2
2 2
1 2 1 2 1 2
2 30
x x x x x x
.
Câu 10. [0D3.3-2] Gọi
0
m
là giá trị của
m
để hệ phương trình
3
2
9
x y m
mx y m
có vô số nghiệm. Khi đó:
A.
0
1
1;
2
m
. B.
0
1
0;
2
m
. C.
0
1
;2
2
m
. D.
0
1
;0
2
m
.
Lời giải
Chọn B.
Từ 3
x y m
3
x m y
thay vào
2
9
mx y m
ta được:
2
3
9
m m y y m
2
2
1 3
9
m y m m
.
Hệ có vô số nghiệm
2
1 3 0
1
2
3
0
9
m
m
m m
.
Câu 11. [0D3.3-2] Hệ phương trình
3
3
2019
2019
x y x
y x y
có số nghiệm là
A.
4
. B.
6
. C.
1
. D.
3
.
Lời giải
Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/21
Trừ hai phương trình theo vế ta được:
3 3
2019 2019
x y y x x y
2 2
2018 0
x y x xy y
2
2
1 3
2018 0
2 4
x y x y y
x y
vì biểu
thức
2
2
1 3
2018 0, ,
2 4
x y y x y
.
Với
y x
ta được:
3
2020 0
x x
2
2020 0
x x
0 0
2020 2020
2020 2020
x y
x y
x y
.
Vậy hệ đã cho có
3
nghiệm.
Câu 12. [0D3.2-1] Số nghiệm của phương trình
2
1 2
x x
là
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn A.
2
1 2
x x
2
2
2
2 0
1 2
x
x x
2 2
2
1 3 0
x
x x x x
2
2
3 0
x
x x
2
13 1
2
13 1
2
x
x
x
(Vô nghiệm).
Câu 13. [0D2.1-2] Tập xác định của hàm số
1
1
4
y x
x
là
A.
1;4
. B.
1;4
. C.
1;4
. D.
1;4
.
Lời giải
Chọn A.
Hàm số xác định khi:
1 0
4 0
x
x
1
4
x
x
1 4
x
.
Vậy tập xác định của hàm số là
1;4
.
Câu 14. [0H2.2-2] Cho
ABC
có
1;2
A ,
0;3
B ,
5; 2
C
. Tìm tọa độ chân đường cao hạ từ đỉnh
A
của
ABC
.
A.
0;3
. B.
0; 3
. C.
3;0
. D.
3;0
.
Lời giải
Chọn A.
1;1
AB
;
5; 5
BC
. 5 5 0
AB BC
AB BC
, suy ra
ABC
vuông tại
B
.
Vậy chân đường cao hạ từ
A
trùng với đỉnh
B
của
ABC
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/21
Câu 15. [0D2.2-2] Cho các đường thẳng:
1
3
: 2
3
d y x
;
2
1
: 1
3
d y x
;
3
3
: 1 2
3
d y x
;
4
3
: 1
3
d y x
. Khẳng định nào đúng trong các khẳng định sau?
A.
2
d
,
3
d
,
4
d
song song với nhau. B.
2
d
và
4
d
song song với nhau.
C.
1
d
và
4
d
vuông góc với nhau. D.
2
d
và
3
d
song song với nhau.
Lời giải
Chọn B.
Các đường thẳng được viết lại như sau:
1
: 3 2
d y x
;
2
3
: 1
3
d y x
;
3
3
: 1
3
d y x
;
4
3
: 1
3
d y x
.
Ta thấy
2
d
trùng với
3
d
nên loại A và D.
Đường thẳng
2
d
và
4
d
có cùng hệ số góc
3
3
k và tung độ góc khác nhau nên
2
d
và
4
d
song song với nhau.
Câu 16. [0D3.2-2] Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A.
ĐKXĐ:
3
3
1
x
x
x
.
Phương trình
2
3 2 3
0
1
x x x
x
2
3 2 0
3 0
x x
x
1
2
3
x l
x l
x tm
.
Vậy phương trình có nghiệm duy nhất
3
x
.
Câu 17. [0D2.3-2] Có bao nhiêu giá trị nguyên của
m
để đường thẳng
3
y mx
không có điểm chung
với Parabol
2
1
y x
?
A.
6
. B.
9
. C.
7
. D.
8
.
Lời giải
Chọn C.
Phương trình hoành độ giao điểm của đường thẳng
3
y mx
và Parabol
2
1
y x
là
2
1 3
x mx
2
4 0
x mx
.
Điều kiện để đường thẳng
3
y mx
không có điểm chung với Parabol
2
1
y x
là phương
trình trên vô nghiệm, hay
2
16 0
m
4 4
m
.
Mà
m
là số nguyên nên
3; 2; 1;0
m .
Câu 18. [0D3.2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2
0
3
x m x m
x
có
nghiệm
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/21
A.
; 1
m

. B.
1;m

. C.
1;m

. D.
m R
.
Lời giải
Chọn B.
ĐKXĐ:
3
x
.
2
0
3
x m x m
x
2 0
x m x m
3
x m
.
Phương trình có nghiệm
3 3
m
1
m
.
Câu 19. [0D2.1-1] Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số
2
2 2
y x x
xác định trên R. B. Hàm số
3
y x
là hàm số lẻ.
C. Hàm số
2
1
y x
là hàm số chẵn. D. Hàm số
2
1
y x
là hàm số chẵn.
Lời giải
Chọn C.
Xét hàm số
2
1
y x
có TXĐ:
D
.
Ta có
2
2
2 2 1 9
2 2 1 1
f
f
2 2
f f nên hàm số không chẵn.
Câu 20. [0D3.3-2] Phương trình
3 2 5
x x
có hai nghiệm
1
x
,
2
x
. Tính
1 2
x x
A.
14
3
. B.
28
3
. C.
7
3
. D.
14
3
.
Lời giải
Chọn D.
Xét phương trình:
3 2 5
x x
3 2 5
3 5 2
x x
x x
8
3
2
x
x
1 2
14
3
x x
.
Câu 21. [0H2.2-2] Cho
3;4
A ,
2;1
B ,
0;5
C . Tính độ dài trung tuyến
AM
của
ABC
.
A.
13
. B.
5
. C.
4
. D.
17
.
Lời giải
Chọn D.
Gọi
;
M x y
là trung điểm
BC
suy ra
1; 3
M
2 2
1 3 3 4
AM
17
.
Câu 22. [0D2.3-3] Số giá trị nguyên của
m
để phương trình
2
4 1
x m
có bốn nghiệm phân biệt là
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn C.
Xét
2
4 1
x m
1
.
Ta thấy số nghiệm của
1
là số giao điểm của hai đồ thị
2
4
y x f x
và
1
y m
.
Vẽ đồ thị hàm số
2
4
y x
:
Vẽ
2
4
y f x x
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/21
Bằng cách giữ nguyên phần đồ thị của hàm số
2
4
y f x x
phía trên trục hoành và lấy
đối xứng phần đồ thị hàm số
2
4
y f x x
phía dưới trục hoành qua trục hoành, ta
được đồ thì hàm số
2
4
y x
như sau:
Từ đồ thị, ta thấy để hai đồ thị hàm số
2
4
y x f x
và
1
y m
cắt nhau tại bốn điểm
phân biệt
0 1 4
m
1 3
m
.
Do
m
là số nguyên nên
0
m
,
1
m
,
2
m
. Vậy có
3
giá trị
m
thỏa mãn.
Câu 23. [0H1.3-2] Cho
ABC
vuông cân tại
A
,
AB a
. Tính độ dài vectơ
4
AB AC

.
A.
20
a
. B.
5
a
. C.
17
a
. D.
17
a
.
Lời giải
Chọn D.
Xét hình vẽ sau:
Dựng
4
AM AC
và hình bình hành
BAMN
như trên, khi đó:
4
AB AC
AB AM
AN
AN
2
2
4
a a
17
a .
Câu 24. [0D3.2-3] Cho phương trình
1 5 3. 1 5
x x x x m
. Có tất cả bao nhiêu giá trị
nguyên của tham số
m
để phương trình trên có nghiệm?
A.
6
. B.
8
. C.
7
. D. vô số.
Lời giải
Chọn C.
Xét
1 5 3. 1 5
x x x x m
1
.
Điều kiện:
1 5
x
.
Đặt 1 5
t x x
0
t
.
Có
2
4 2 1. 5
t x x
2
t
và
2
4 2 1. 5 4 1 5 8
t x x x x
Do đó, điều kiện của
t
là
2 2 2
t
.
A
B
N
M
C
4
a
a
x
y
O
2
4
2
x
y
O
2
4
2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/21
Khi đó
1
2
4
3.
2
t
t m
2
3 2 12 2
t t m
với
2 2 2
t
.
Yêu cầu bài toán
Tìm
m
để hai đồ thị hàm số
2
3 2 12
y t t
với
2 2 2
t
và
2
y m
có điểm chung.
Bảng biến thiên của hàm số
2
3 2 12
y t t
với
2 2 2
t
Ta thấy rõ ràng trên
2;2 2
thì
4 12 4 2
y .
Nên yêu cầu thỏa mãn khi
4 2 12 4 2
m
2 6 2 2 8,83
m .
Do
m
là số nguyên nên
2;3;...;8
m . Vậy có
7
giá trị
m
thỏa mãn.
Câu 25. [0D3.2-2] Biết phương trình
4 2 2
3 1 0
x mx m
có bốn nghiệm phân biệt
1
x
,
2
x
,
3
x
,
4
x
.
Tính
1 2 3 4 1 2 3 4
M x x x x x x x x
.
A.
2
1.
M m
B.
3 .
M m
C.
3 .
M m
D.
2
1.
M m
Lời giải
Chọn A.
Đặt
2
0
t x
suy ra phương trình trở thành
2 2
3 1 0 *
t mt m .
Biết phương trình ban đầu có bốn nghiệm
1
x
,
2
x
,
3
x
,
4
x
nên phương trình
*
có hai nghiệm
1 2
0
t t
.
Không mất tính tổng quát giả sử
1 1
x t
,
2 2
x t
,
3 2
x t
,
4 1
x t
.
Khi đó
2
1 2 3 4 1 2 3 4 1 2
. 1
M x x x x x x x x t t m
.
Câu 26. [0D2.2-2] Tìm
a
,
b
để đồ thị hàm số
y ax b
đi qua hai điểm
1; 2
A
,
3;5
B .
A.
7 1
,
4 4
a b
. B.
7 1
,
4 4
a b
. C.
1 7
,
4 4
a b
. D.
1 4
,
7 7
a b
.
Lời giải
Chọn B.
Vì
1; 2
A
,
3;5
B nằm trên đồ thị hàm số
y ax b
nên ta có:
7
2
4
.
3 5 1
4
a
a b
a b
b
Câu 27. [0D3.2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2
m m x mx x m
nghiệm đúng với mọi
m
.
A.
2
m
. B.
2.
m
C.
1.
m
D.
1
m
.
Lời giải
Chọn C.
Ta có:
2 2
2 2 1 2 2
m m x mx x m m x m
.
Để phương trình nghiệm đúng với mọi
m
thì
2
1 0
1
2 2 0
m
m
m
.
t
2
2 2
y
4
12 4 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/21
Câu 28. [0D3.2-2] Biết phương trình
2
1 3 3 1
x x x
có hai nghiệm
1
x
,
2
x
. Tính giá trị biểu
thức
1 2
1 . 1
x x
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn B.
Điều kiện
1
x
.
2
1 3 3 1
x x x
1 1 3 1 1
x x x
1 0
1 1 3
x
x
1
3 2 3
x
x
Do đó
1 2
1 . 1 0
x x
.
Câu 29. [0D2.3-3] Xác định hàm số
2
y ax bx c
biết đồ thị của hàm số đó cắt trục tung tại điểm có
tung độ là
3
và giá trị nhỏ nhất của hàm số là
25
8
tại
1
4
x
.
A.
2
2 3
y x x
. B.
2
1
3
2
y x x
. C.
2
2 3
y x x
. D.
2
2 3
y x x
.
Lời giải
Chọn A.
Từ giả thiết ta có hệ:
3
1
2 4
25
4 8
c
b
a
a
2
3
2
2 8 25
c
a b
b ac a
2
2
3
2 8 2 3 25 2
a b
c
b b b
3
0 loai
1
2
c
b
b
a b
2
1
3
a
b
c
Câu 30. [0D1.3-2] Cho các tập hợp:
A
{cam, táo, mít, dừa} ;
B
{táo, cam} ;
C
{dừa, ổi, cam, táo, xoài}. Tập
\
A B C
là
A. {táo, cam}. B. {mít}. C. {mít, dừa}. D. {dừa}.
Lời giải
Chọn D.
\
A B
mít, dừa
, suy ra
\
A B C
dừa
Câu 31. [0D3.3-2] Hệ phương trình
2
1
2 2 2 0
x y
x x y
có số nghiệm là
A.
1
. B.
2
. C.
4
. D.
0
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/21
Lời giải
Chọn A.
2
1
2 2 2 0
x y
x x y
2
1
2 2 1 2 0
y x
x x x
2
1
4 4 0
y x
x x
2
1
x
y
.
Vậy hệ phương trình có nghiệm duy nhất là
2; 1
.
Câu 32. [0D3.2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 4 0
x m x m
có
hai nghiệm phân biệt.
A.
6
m
. B.
6
m
. C.
6
m
. D.
m
.
Lời giải
Chọn C.
Cách 1. Phương trình có hai nghiệm phân biệt
0
0
a
2
2 0
4 4 8 32 0
m m m
2
12 36 0
m m
2
6 0
m
6
m
.
Cách 2.
2
2 2 4 0
x m x m
1
4
2
x
m
x
(do
0
a b c
).
Phương trình có hai nghiệm phân biệt
4
1
2
m
6
m
.
Câu 33. [0D3.3-3] Hệ phương trình
2
2 2
2
2 9
x xy
x xy y
có nghiệm là
0 0
;
x y
thỏa mãn
0
1
x
. Tính
0 0
x y
.
A.
4
. B.
5
. C.
1
. D.
3
.
Lời giải
Chọn D.
2
2 2
2
2 9
x xy
x xy y
2
2 2
9 9 18
4 2 2 18
x xy
x xy y
2
2 2 2
9 9 18
4 2 2 9 9
x xy
x xy y x xy
2
2 2
9 9 18
5 11 2 0
x xy
x xy y
2
9 9 18
2 5 0
x xy
x y x y
2
2
2
2
2
5
x xy
x
y
x xy
y x
2
2
4
2
4 2
loai
5
x
x
y
x
y x
2
1
2
1
x
y
x
y
.
Mà
0
1
x
nên
0
2
x
,
0
1
y
. Vậy
0 0
3
x y
.
Câu 34. [0H2.3-3] Cho
4
a b
,
2
a
,
3
b
. Tính
a b
.
A.
3
. B.
10
. C.
12
. D.
2
.
Lời giải
Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/21
Gọi
3
điểm
A
,
B
,
C
thỏa mãn
AB a
,
BC b
.
Suy ra
3
điểm
A
,
B
,
C
lập thành một tam giác với
2
AB
,
3
BC
,
4
CA
.
Ta có
a b AB BC

AC
, với
C
là điểm đối xứng của
C
qua
B
.
Áp dụng công thức trung tuyến cho tam giác
ACC
ta có
2 2 2
2
2 4
AC AC CC
AB
Suy ra
2 2 2
2
4 2
2
AB CC AC
AC
2
4.4 36 2.16
2
AC
10
AC
.
Câu 35. [0D1.3-3] Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa.
Biết rằng mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là có 4 bạn thích cả ba môn;
có 9 bạn thích Văn và Sử; có 5 bạn thích Sử và Địa; có 11 bạn thích Văn và Địa; có 24 bạn
thích Văn; có 19 bạn thích Sử và có 22 bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa?
A.
21
. B.
23
. C.
24
. D.
22
.
Lời giải
Chọn D.
Gọi
V
,
S
,
Đ
lần lượt là tập hợp các học sinh thích môn Văn, môn Sử và môn Địa.
Ta có biểu đồ Ven thể hiện mối quan hệ giữa các tập hợp trên như hình vẽ.
Suy ra tổng số các học sinh không thích môn Địa là
8 5 9 22
.
Câu 36. [0H2.3-3] Cho
1;4
M ,
1;3
N ,
0;6
P . Gọi
;
Q a b
là điểm thỏa mãn
NPMQ
là hình
bình hành. Tổng
a b
bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D.
Ta có
1; 3
PN
và
1; 4
MQ a b
.
Tứ giác
NPMQ
là hình bình hành khi và chỉ khi
PN MQ
1 1
4 3
a
b
0
1
a
b
.
Do đó,
1
a b
.
Câu 37. [0H2.3-2] Cho
ABC
có
5
AB
,
40
A
,
60
B
. Độ dài
BC
gần nhất với kết quả nào?
A.
3,7
. B.
3,3
. C.
3,5
. D.
3,1
.
Lời giải
A
4
3
2
C
B
C
V
S
Đ
4
8
5
1
9
10
7
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/21
Chọn A.
Ta có
180 80
C A B
Áp dụng định lí sin:
sin sin
BC AB
A C
5.sin40
3,7
sin80
BC
.
Câu 38. [0H2.2-2] Cho
ABC
đều,
6
AB
và
M
là trung điểm của
BC
. Tích vô hướng
.
AB MA
bằng
A.
18
. B.
27
. C.
18
. D.
27
.
Lời giải
Chọn D.
Ta có
. . .cos150
AB MA AB MA

3
6.3 3. 27
2
.
Câu 39. [0H2.2-1] Cho
0;3
A ,
4;0
B ,
2; 5
C
. Tính
.
AB BC

.
A.
16
. B.
9
. C.
10
. D.
9
.
Lời giải
Chọn D.
Ta có
4; 3
AB
;
6; 5
BC
. 4. 6 3 . 5 9
AB BC
.
Câu 40. [0H2.2-1] Cho hai vectơ
a
,
b
khác vectơ
0
thỏa mãn
1
. .
2
a b a b
. Khi đó góc giữa hai
vectơ
a
,
b
là
A.
60
. B.
120
. C.
150
. D.
30
.
Lời giải
Chọn A.
Ta có
1
. .
2
a b a b
1
. .cos , .
2
a b a b a b
1
cos ,
2
a b
, 60
a b
.
Câu 41. [0D2.2-1] Tìm tất cả các giá trị của tham số
m
để hàm số
1 . 2
y m x m
đồng biến
trên
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn C.
Ta có
1 . 2
y m x m
1 2
y m x m
.
Hàm số đồng biến trên
khi
1 0
m
1 0
m
1
m
.
Câu 42. [0H2.2-3] Cho tam giác đều
ABC
, gọi
D
là điểm thỏa mãn
2
DC BD

. Gọi
R
và
r
lần lượt
là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác
ADC
. Tính tỉ số
R
r
.
A.
5
2
. B.
5 7 7
9
. C.
7 5 5
9
. D.
7 5 7
9
.
Lời giải
Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/21
Đặt
AB BC CA a
.
Có
2 2
DC BD DB

2 2
DC DC BC
2
3
DC BC
, nên
2
3
a
DC ,
3
a
BD
.
Áp dụng định lý cosin trong tam giác
ADC
, ta có:
2 2 2
2 . .cos
AD AC DC AC DC ACD
2
2
2 2
2 cos60
3 3
a a
a a
2
7
9
a
.
Suy ra
2
7 7
9 3
a a
AD .
Khi đó, tam giác
ADC
có:
. .
.
4 2
ADC
AD DC CA AD DC CA
S r
R
.
Mà
2
3
ADC ABC
S S
2 2
2 3 3
3 4 6
a a
.
Nên
. .
4
ADC
AD DC CA
R
S
2
7 2
3 3
3
4
6
a a
a
a
21
9
a
.
Và
2.
ADC
S
r
AD DC CA
2
3
2
6
7 2
3 3
a
a a
a
3
5 7
a
.
Do đó, ta có được:
21 3
:
9
5 7
R a a
r
5 7 . 7
9
7 5 7
9
.
Câu 43. [0D3.1-2] Phương trình
2
2 1 2 1 2
x x x x x
có số nghiệm là
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn D.
Điều kiện xác định:
2 0 2
x x
.
2
2 1 2 1 2
x x x x x
2
1 2 1
x x x
2
2
2 1 0
1 2 1
x
x x x
2
1
2
3 3 0
x
x x
B
A
C
D
a
2
3
a
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/21
1
2
0
1
x
x
x
1
x
(không thỏa mãn điều kiện)
Vậy phương trình cho vô nghiệm.
Câu 44. [0H2.3-3] Cho
ABC
có
2
AB
,
3
AC
,
60
A . Tính độ dài đường phân giác trong góc
A
của tam giác
ABC
.
A.
12
5
. B.
6 2
5
. C.
6 3
5
. D.
6
5
.
Lời giải
Chọn C.
Gọi
AD
là đường phân giác trong của góc
A
.
Ta có
ABD ACD ABC
S S S
1 1 1
. . .sin . . .sin . . .sin
2 2 2 2 2
A A
AD AB AD AC AB AC A
.sin . . .sin
2
A
AD AB AC AB AC A
. .sin
.sin
2
AB AC A
AD
A
AB AC
2.3.sin60 6 3
2 3 .sin30 5
AD
.
Câu 45. [0H2.3-2] Tính diện tích
ABC
biết
3
AB
,
5
BC
,
6
CA
.
A.
56
. B.
48
. C.
6
. D.
8
.
Lời giải
Chọn A.
Nửa chu vi của tam giác
ABC
là
3 5 6
7
2 2
AB BC CA
p
.
Áp dụng công thức Hê-rông
ABC
S p p a p b p c
7 7 5 . 7 6 7 3 56
(đvdt).
Câu 46. [0H2.3-2] Cho
ABC
có
3
AB
,
5
BC
và độ dài trung tuyến
13
BM . Tính độ dài
AC
.
A.
11
. B.
4
. C.
9
2
. D.
10
.
Lời giải
Chọn B.
Áp dụng công thức tính độ dài đường trung tuyến ta có
A
C
B
2
3
D
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/21
2 2 2
2
2 4
BA BC AC
BM
2 2 2 2
2 4
AC BA BC BM
2 2 2
2 3 5 4.13
AC
2
16
AC
4
AC
.
Câu 47. [0H2.3-2] Cho
ABC
vuông ở
A
, biết
30
C
,
3
AB
. Tính độ dài trung tuyến
AM
.
A.
3
. B.
4
. C.
5
2
. D.
7
2
.
Lời giải
Chọn A.
Do tam giác
ABC
vuông ở
A
,
30
C
,
3
AB
nên
6
sin30
AB
BC
.
Độ dài đường trung tuyến
1
3
2
AM BC
.
Câu 48. [0D3.2-2] Tìm tất cả các giá trị của tham số
m
để phương trình
2 2
1 1 3 0
m x m x
có
hai nghiệm trái dấu.
A.
1
m
. B.
0
m
. C.
0
m
. D.
1
m
.
Lời giải
Chọn A.
Phương trình
2 2
1 1 3 0
m x m x
có hai nghiệm trai dấu khi và chỉ khi
1 0
3 1 0
m
m
1
1
m
m
1
m
.
Vậy
1
m
thì phương trình đã cho có hai nghiệm trái dấu.
Câu 49. [0D2.3-3] Cho hàm số
2
2 8 khi 2
2 12 khi 2
x x x
y
x x
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của hàm số khi
1;4
x . Tính
M m
.
A.
14
. B.
13
. C.
4
. D.
9
.
Lời giải
Chọn B.
Ta có đồ thị của hàm số khi
1;4
x như hình vẽ dưới đây:
Dựa vào đồ thị ta có
4
M
,
9
m
13
M m
.
A
B
M
C
3
30
x
y
O
4
5
9
8
4
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/21
Câu 50. [0D3.3-3] Biết hệ phương trình
2 4
2 3
y x xy
y x xy
có nghiệm
0 0
;
x y
với
0
0
x
. Tỉ số
0
0
y
x
bằng
A.
2
. B.
1
2
. C.
1
. D.
1
.
Lời giải
Chọn A.
Ta có:
2 4
2 3
y x xy
y x xy
3 6 12
8 4 12
y x xy
y x xy
2 4
5 10 0
y x xy
y x
2 4
2
y x xy
y x
2 2 4 .2
2
x x x x
y x
2
4 8
2
x x
y x
0
0
1
2
1
x
y
x
y
.
Vì
0
0
x
nên tỉ số
0
0
2
y
x
.
----------HẾT----------
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI HỌC KỲ I – NĂM HỌC 2018 – 2019
TRƯỜNG THPT LƯƠNG THẾ VINH Môn: TOÁN 10
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm) Mã đề thi 132
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Câu 1: Gọi m , m là hai giá trị khác nhau của m để phương trình 2 2
x  3x m  3m  4  0 có hai 1 2
nghiệm phân biệt x , x sao cho x  2x . Tính m m m m . 1 2 1 2 1 2 1 2 A. 4 . B. 3 . C. 5 . D. 6 .
Câu 2: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?
a) Số 2 là số nguyên tố. b) Số 2018 3 1 chia hết cho 2.
c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của hình bình hành đó.
d) Mọi hình chữ nhật luôn có chiều dài lớn hơn chiều rộng.
e) Một số chia hết cho 28 thì chia hết cho 8. A. 3 . B. 1. C. 2 . D. 4 .
Câu 3: Gọi m là giá trị của tham số m để phương trình m  2 x   x  
1  0 vô nghiệm. Khẳng định 0 nào sau đây là đúng? A. m   . B. m  2; 0 . C. m  0;1 . D. m  1;1 . 0   0   0   0
Câu 4: Cho hình vuông ABCD tâm O . Đẳng thức nào sau đây là sai?
  
      
A. DA OC OB .
B. AO DO CD . C. AB DC .
D. BO DO AC .
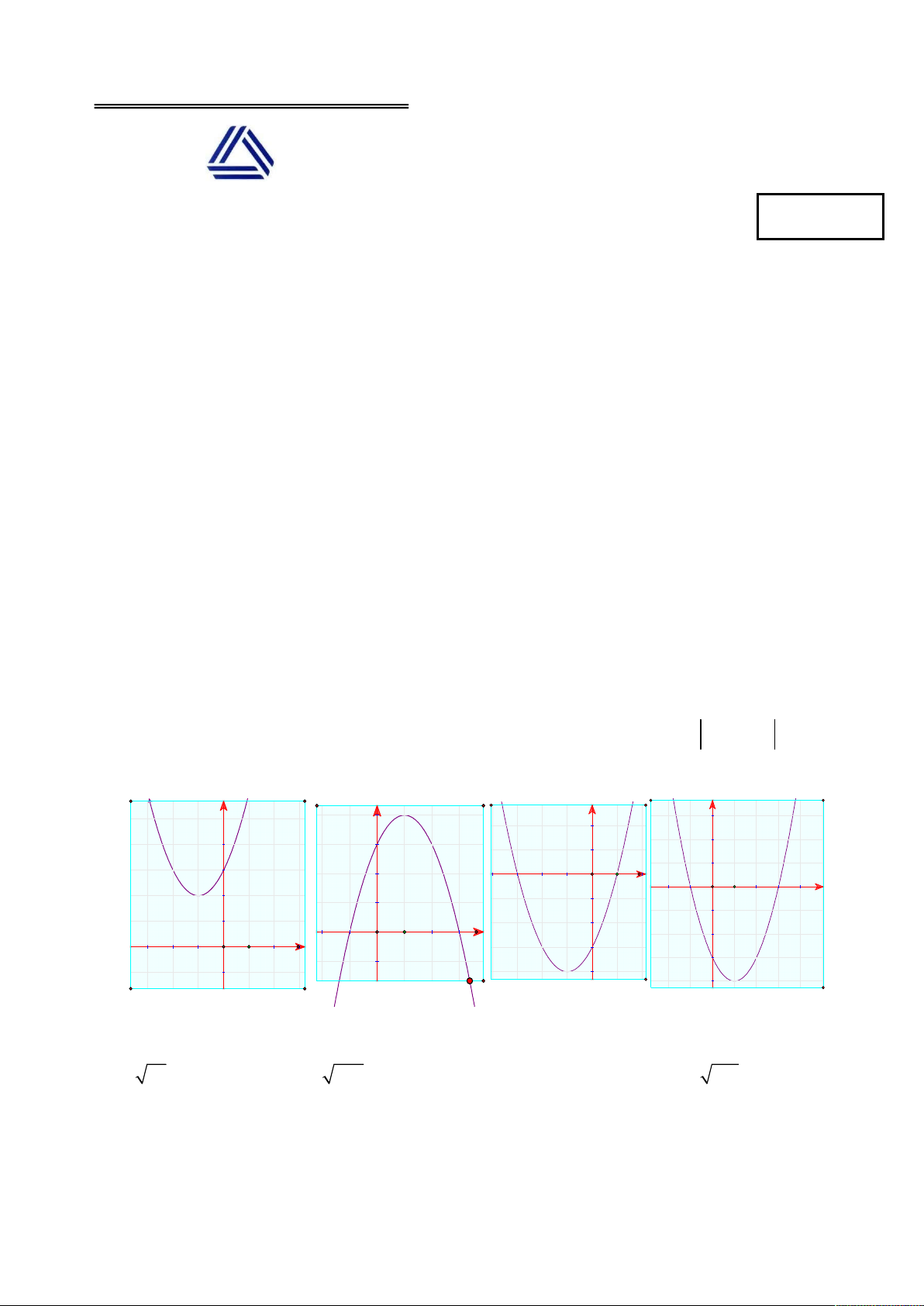
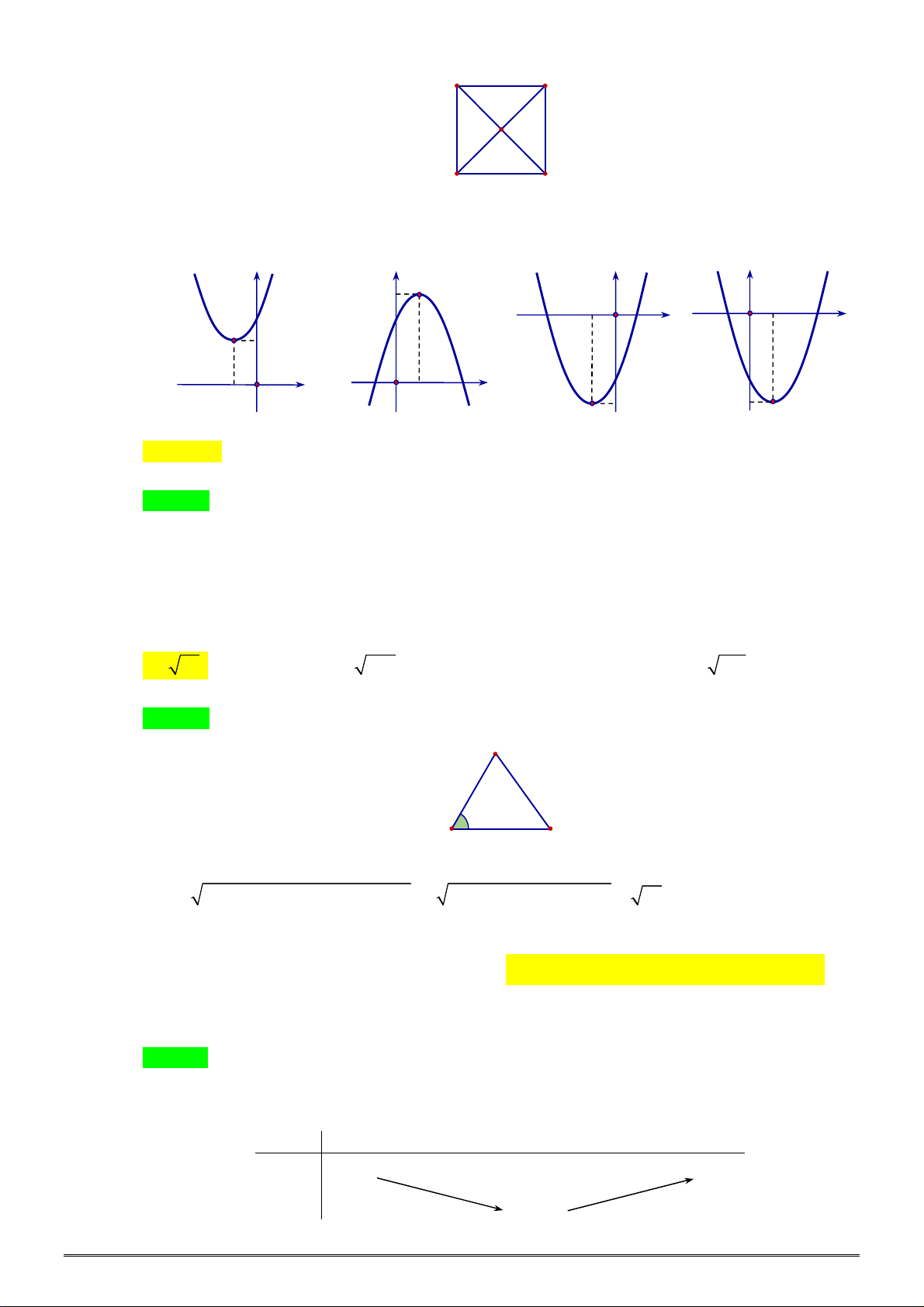
Câu 5: Đồ thị nào sau đây là đồ thị của hàm số 2
y x  2x  3 : y y y y O 1 x x O 1 O 1 x O 1 x Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Câu 6: Cho ABC có AB  9 , BC  8 ,  0
B  60 . Tính độ dài AC . A. 73 . B. 217 . C. 8 . D. 113 . Câu 7: Cho hàm số 2
y x  4x 1. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số nghịch biến trên khoảng  ;  3 .
B. Hàm số đồng biến trên khoảng 3;  .
C. Hàm số có giá trị nhỏ nhất là 3  .
D. Đồ thị hàm số đi qua điểm A0;  1 .
Trang 1/5 - Mã đề thi 132 3
  x  2 khi 1  x  2 
Câu 8: Cho hàm số f x  
. Tính giá trị f 3 . 2
x  4 khi x  2  A. Không xác định.
B. f 3  5 hoặc f 3  3. C. f 3  5 . D. f 3  3.
Câu 9: Tính tổng bình phương các nghiệm của phương trình 2
x  2x 13  0 . A. 22 . B. 4 . C. 30 . D. 28 .
x  3y m
Câu 10: Gọi m là giá trị của m để hệ phương trình
có vô số nghiệm. Khi đó: 0  2
mx y m    9  1   1   1   1  A. m  1  ;  . B. m  0; . C. m  ; 2 . D. m   ; 0 . 0   0   0   0    2   2   2   2  3 
x  2019 y x
Câu 11: Hệ phương trình  có số nghiệm là: 3
y  2019x y  A. 4 . B. 6 . C. 1. D. 3 .
Câu 12: Số nghiệm của phương trình 2
x 1  x  2 là: A. 0 . B. 2 . C. 3 . D. 1. 1
Câu 13: Tập xác định của hàm số y x 1  là: 4  x A. 1; 4 . B. 1; 4 . C. 1; 4. D. 1; 4 .
Câu 14: Cho ABC có A1; 2 , B 0;3 , C 5; 2
  . Tìm tọa độ chân đường cao hạ từ đỉnh A của ABC . A. 0;3 . B. 0; 3 . C. 3;0 . D.  3  ; 0 .
Câu 15: Cho các đường thẳng sau. 3 1  3  3 d : y x  2 d : y x 1
d : y   1 x   2 d : y x 1 1 2 3 4 3 3  3    3
Khẳng định nào đúng trong các khẳng định sau?
A. d , d , d song song với nhau.
B. d và d song song với nhau. 2 3 4 2 4
C. d và d vuông góc với nhau.
D. d và d song song với nhau. 1 4 2 3  2
x  3x  2 x  3
Câu 16: Số nghiệm của phương trình  0 là: x 1 A. 1. B. 2 . C. 3 . D. 0 .
Câu 17: Có bao nhiêu giá trị nguyên của m để đường thẳng y mx  3 không có điểm chung với Parabol 2 y x 1? A. 6 . B. 9 . C. 7 . D. 8 .
2 x m  x m
Câu 18: Tìm tất cả các giá trị của tham số m để phương trình  0 có nghiệm. x  3 A. m   ;    1 .
B. m  1;  . C. m  1  ;  . D. m R .
Câu 19: Chọn khẳng định sai trong các khẳng định sau: A. Hàm số 2 y
x  2x  2 xác định trên R. B. Hàm số 3
y x là hàm số lẻ.
C. Hàm số y   x  2 1 là hàm số chẵn. D. Hàm số 2
y x 1 là hàm số chẵn.
Trang 2/5 - Mã đề thi 132
Câu 20: Phương trình 3  x  2x  5 có hai nghiệm x , x . Tính x x . 1 2 1 2 14 28 7 14 A.  . B.  . C. . D. . 3 3 3 3
Câu 21: Cho A3; 4 , B  2  ; 
1 , C 0;5 . Tính độ dài trung tuyến AM của ABC . A. 13 . B. 5 . C. 4 . D. 17 .
Câu 22: Số giá trị nguyên của m để phương trình 2
x  4  m 1 có bốn nghiệm phân biệt là: A. 4 . B. 2 . C. 3 . D. 5 .  
Câu 23: Cho ABC vuông cân tại A , AB a . Tính độ dài vectơ AB  4AC . A. 20a . B. 5a . C. 17a . D. 17a . Câu 24: Cho phương trình
x 1  5  x  3.  x  
1 5  x  m . Có tất cả bao nhiêu giá trị nguyên của
tham số m để phương trình trên có nghiệm? A. 6 . B. 8 . C. 7 . D. vô số.
Câu 25: Biết phương trình 4 2 2
x  3mx m 1  0 có bốn nghiệm phân biệt x , x , x , x . Tính 1 2 3 4
M x x x x x .x .x .x được kết quả là: 1 2 3 4 1 2 3 4 A. 2 M m 1. B. M  3  m . C. M  3m . D. 2
M  m 1.
Câu 26: Tìm a, b để đồ thị hàm số y ax b đi qua hai điểm A1; 2   , B  3  ;5 . 7 1 7 1 1 7 1 4 A. a  ;b  .
B. a   ;b   .
C. a   ;b   .
D. a   ;b   . 4 4 4 4 4 4 7 7
Câu 27: Tìm tất cả các giá trị của tham số m để phương trình  2
m mx  2  mx x  2m nghiệm đúng với x   R . A. m  2 . B. m  2 . C. m  1. D. m  1  .
Câu 28: Biết phương trình 2
x 1  3x  3 
x 1 có hai nghiệm x , x . Tính giá trị biểu thức 1 2
x 1 . x 1 . 1   2  A. 1. B. 0 . C. 2 . D. 3 .
Câu 29: Xác định hàm số 2
y ax bx c biết đồ thị của hàm số đó cắt trục tung tại điểm có tung độ là 25 1 3
 và giá trị nhỏ nhất của hàm số là  tại x  . 8 4 1 A. 2
y  2x x  3 . B. 2 y x x  3 . C. 2
y  2x x  3 . D. 2
y  2x x  3 . 2
Câu 30: Cho các tập hợp :
A  {cam, táo, mít, dừa} B  {táo, cam}
C  {dừa, ổi, cam, táo, xoài}
Tập  A \ B  C là : A. {táo, cam}. B. {mít}. C. {mít, dừa}. D. {dừa}. x y  1
Câu 31: Hệ phương trình  có số nghiệm là: 2
x  2x  2 y  2  0  A. 1. B. 2 . C. 4 . D. 0 .
Câu 32: Tìm tất cả các giá trị của tham số m để phương trình 2
2x  m  2 x m  4  0 có hai nghiệm phân biệt. A. m  6 . B. m  6 . C. m  6 . D. m  .
Trang 3/5 - Mã đề thi 132 2 
x xy  2
Câu 33: Hệ phương trình 
có nghiệm là  x ; y thỏa mãn x  1. Tính x y : 0 0  2 2 0 0 0
2x xy y  9  A. 4 . B. 5 . C. 1. D. 3 .      
Câu 34: Cho a b  4 , a  2 , b  3 . Tính a b . A. 3 . B. 10 . C. 12 . D. 2 .
Câu 35: Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa. Biết rằng
mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là: có 4 bạn thích cả ba môn; có 9 bạn thích Văn
và Sử; có 5 bạn thích Sử và Địa; có 11 bạn thích Văn và Địa; có 24 bạn thích Văn; có 19 bạn thích Sử và
có 22 bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa? A. 21 . B. 23 . C. 24 . D. 22 .
Câu 36: Cho M 1; 4 , N  1
 ;3 , P 0;6 . Gọi Q  ;
a b là điểm thỏa mãn NPMQ là hình bình hành.
Tổng a b bằng: A. 1. B. 0 . C. 2 . D. 1.
Câu 37: Cho ABC có AB  5 ,  0 A  40 ,  0
B  60 . Độ dài BC gần nhất với kết quả nào? A. 3, 7 . B. 3, 3 . C. 3, 5 . D. 3,1.  
Câu 38: Cho ABC đều , AB  6 và M là trung điểm của BC .Tích vô hướng . AB MA bằng: A. 18  . B. 27 . C. 18 . D. 27  .  
Câu 39: Cho A0;3 , B 4;0 , C  2  ; 5   . Tính . AB BC . A. 16 . B. 9 . C. 10  . D. 9  .      1    
Câu 40: Cho hai vectơ a, b khác vectơ 0 thỏa mãn . a b
a . b . Khi đó góc giữa hai vectơ a,b là: 2 A. 0 60 . B. 0 120 . C. 0 150 . D. 0 30 .
Câu 41: Tìm tất cả các giá trị của tham số m để hàm số y  m  
1 .x  2m đồng biến trên . A. m  1. B. m  1. C. m  1. D. m  1.  
Câu 42: Cho tam giác đều ABC, gọi D là điểm thỏa mãn DC  2BD . Gọi R và r lần lượt là bán kính R
đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số . r 5 5  7 7 7  5 5 7  5 7 A. . B. . C. . D. . 2 9 9 9 Câu 43: Phương trình 2
x  2  x x 1  2x 1 x  2 có số nghiệm là: A. 1. B. 3 . C. 2 . D. 0 .
Câu 44: Cho ABC có AB  2 , AC  3 ,  0
A  60 . Tính độ dài đường phân giác trong góc A của tam giác ABC 12 6 2 6 3 6 A. . B. . C. . D. . 5 5 5 5
Câu 45: Tính diện tích ABC biết AB  3, BC  5, CA  6 . A. 56 . B. 48 . C. 6 . D. 8 .
Câu 46: Cho ABC có AB  3, BC  5 và độ dài trung tuyến BM  13 . Tính độ dài AC . 9 A. 11 . B. 4 . C. . D. 10 . 2
Câu 47: Cho ABC vuông ở A , biết  0
C  30 , AB  3 . Tính độ dài trung tuyến AM . 5 7 A. 3 . B. 4 . C. . D. . 2 2
Trang 4/5 - Mã đề thi 132
Câu 48: Tìm tất cả các giá trị của tham số m để phương trình m   2 x   2 1 m  
1 x  3  0 có hai nghiệm trái dấu. A. m  1. B. m  0 . C. m  0 . D. m  1. 2
x  2x  8 khi x  2
Câu 49: Cho hàm số y  
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ
2x 12 khi x  2 
nhất của hàm số khi x  1
 ; 4 . Tính M m . A. 14 . B. 13  . C. 4 . D. 9  .
y  2x  4xy y
Câu 50: Biết hệ phương trình 
có nghiệm  x ; y với x  0 . Tỉ số 0 bằng: 0 0 
2 y x  3xy 0  x0 1 A. 2 . B. . C. 1. D. 1. 2
----------------------------------------------- ----------- HẾT ----------
Trang 5/5 - Mã đề thi 132 ĐÁP ÁN THAM KHẢO 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A C B A A B C C B D A A A B A C B C D D C D C A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C B A D A C D B D D A D D A C D D C A B A A B A HƯỚNG DẪN GIẢI Câu 1. [0D1.1-2] Gọi
m , m là hai giá trị khác nhau của
m để phương trình 1 2 2 2
x  3x m  3m  4  0 có hai nghiệm phân biệt x , x sao cho x  2x . Tính 1 2 1 2
m m m m . 1 2 1 2 A. 4 . B. 3 . C. 5 . D. 6 . Lời giải Chọn C.
Phương trình có hai nghiệm phân biệt 2  4
m 12m  7  0 . x x  3
Khi đó phương trình có hai nghiệm phân biệt x , x . Theo Vi-et ta có: 1 2 . 1 2  2
x .x m  3m  4  1 2
2x x  3 x  1 m  1
Mà x  2x nên ta có: 2 2 2    . 1 2  2 2 2 
2x m  3m  4
m  3m  2  0  m  2 2  
Vậy m m m m  5 . 1 2 1 2 Câu 2.
[0D3.2-2] Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?
a) Số 2 là số nguyên tố. b) Số 2018 3 1 chia hết cho 2.
c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của hình bình hành đó.
d) Mọi hình chữ nhật luôn có chiều dài lớn hơn chiều rộng.
e) Một số chia hết cho 28 thì chia hết cho 8. A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn A.
Các mệnh đề đúng là a; b.
Chú ý: d) sai vì hình vuông cũng là hình chữ nhật. Câu 3.
[0D3.2-2] Gọi m là giá trị của tham số m để phương trình m  2 x   x   1  0 vô nghiệm. 0
Khẳng định nào sau đây là đúng? A. m  . B. m  2  ; 0 . C. m  0;1 .
D. m  1;1 . 0   0   0   0 Lời giải Chọn B.
Ta có: m  2 x   x  
1  0  m  
1 x 1  0 . Phương trình vô nghiệm  m  1 . Câu 4.
[0H1-2-1] Cho hình vuông ABCD tâm O . Đẳng thức nào sau đây là sai?
  
      
A. DA OC OB .
B. AO DO CD .
C. AB DC .
D. BO DO AC . Lời giải Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/21 A B O D C      
Ta có AO DO OC DO DC CD . Câu 5.
[0D2-3-1] Đồ thị nào sau đây là đồ thị của hàm số 2
y x  2x  3 ? y y y y 4 4 1  1  1 3 3 O 1 x O x 2 3  3  1  O x 1  O 1 3 x 4  4  Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1. Lời giải Chọn A. Đồ thị của hàm số 2
y x  2x  3 có hệ số a  1  0 nên bề lõm hướng lên trên  loại hình 2. Đồ thị của hàm số 2
y x  2x  3 còn có trục đối xứng x  1 , cắt trục tung tại điểm có tọa độ
0;3 , cắt trục hoành tại các điểm 3;0 ,  1
 ;0 do đó ta chọn hình 4.  Câu 6.
[0H2-3-2] Cho tam giác ABC có AB  9 , BC  8 , B  60 . Tính độ dài AC . A. 73 . B. 217 . C. 8 . D. 113 . Lời giải Chọn A. C 8 B 9 A
Áp dụng định lí côsin cho tam giác ABC ta có 2 2 AC
AB BC  2 A . B BC.cos B 2 2
 8  9  2.8.9.cos 60  73 . Câu 7.
[0D2.3-1] Cho hàm số 2
y x  4x 1. Chọn khẳng định đúng trong các khẳng định sau::
A. Hàm số nghịch biến trên khoảng  ;  3 .
B. Hàm số đồng biến trên khoảng 3; .
C. Hàm số có giá trị nhỏ nhất là 3  .
D. Đồ thị hàm số đi qua điểm A 0;  1 . Lời giải Chọn B. Đỉnh I 2; 5   .
Vì a  1  0 , nên hàm số có bảng biến thiên: x  2    y 5 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/21
Hàm số đồng biến trên 2;  .
Do đó hàm số đồng biến trên 3; . 3 x  2 khi 1   x  2  Câu 8.
[0D2.1-1] Hàm số f x  
. Tính giá trị f 3 . 2  x  4 khi x  2 
A. Không xác định.
B. f 3  5 hoặc f 3  3.
C. f 3  5 .
D. f 3  3. Lời giải Chọn C. Ta có: f   2 3  3  4  5 . Câu 9.
[0D3.2-1] Tính tổng bình phương các nghiệm của phương trình 2
x  2x 13  0 . A. 2  2 . B. 4 . C. 30 . D. 28 . Lời giải Chọn C. Ta có: .
a c  13  0  phương trình có hai nghiệm trái dấu.
Theo Vi-et ta có: x x  2; x x  13 . 1 2 1 2
Vậy x x   x x 2 2 2  2x x  30 . 1 2 1 2 1 2
x  3y m
Câu 10. [0D3.3-2] Gọi m là giá trị của m để hệ phương trình
có vô số nghiệm. Khi đó: 0  2
mx y m    9  1   1   1   1 
A. m  1;  . B. m  0; . C. m  ; 2 .
D. m   ; 0 . 0   0   0   0    2   2   2   2  Lời giải Chọn B. 2 2
Từ x  3y m x m  3y thay vào mx y m
ta được: m m  3y  y m  9 9 2 1 3m 2
y  m m  . 9 1   3m  0  1 Hệ có vô số nghiệm  2  m  . 2 m m   0 3   9 3 
x  2019 y x
Câu 11. [0D3.3-2] Hệ phương trình  có số nghiệm là 3
y  2019x yA. 4 . B. 6 . C. 1. D. 3 . Lời giải Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/21
Trừ hai phương trình theo vế ta được: 3 3
x  2019 y y  2019x x y 2  1 3   
  x y 2 2
x xy y  2018  0   x y 2  x y  2018  y  
  0  x y vì biểu  2 4      2  1  3 thức 2 x y  2018  y  0, x  , y   .  2  4  x  0  y  0 
Với y x ta được: 3
x  2020x  0  x  2
x  2020  0  x  2020  y  2020  .
x   2020  y   2020 
Vậy hệ đã cho có 3 nghiệm.
Câu 12. [0D3.2-1] Số nghiệm của phương trình 2
x 1  x  2 là A. 0 . B. 2 . C. 3 . D. 1. Lời giải Chọn A. x  2  0 x  2 x  2 2  
x 1  x  2      2 2  2  x  2 1   x  22 2
 x x  
1  x x  3  0
x x  3  0    x  2  13 1   x     2 (Vô nghiệm).    13 1 x    2 1
Câu 13. [0D2.1-2] Tập xác định của hàm số y x 1  là 4  x A. 1;4 . B. 1;4 . C. 1;4. D. 1; 4 . Lời giải Chọn A. x 1  0 x  1
Hàm số xác định khi:     1  x  4 . 4  x  0  x  4 
Vậy tập xác định của hàm số là 1;4 .
Câu 14. [0H2.2-2] Cho A
BC có A 1; 2 , B 0;3 , C 5; 2
  . Tìm tọa độ chân đường cao hạ từ đỉnh A của ABC . A. 0;3 . B. 0; 3   . C. 3;0 . D.  3  ; 0 . Lời giải Chọn A.       AB  1; 
1 ; BC  5; 5  A .
B BC  5  5  0  AB BC , suy ra A
BC vuông tại B .
Vậy chân đường cao hạ từ A trùng với đỉnh B của ABC .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/21 3 1  3 
Câu 15. [0D2.2-2] Cho các đường thẳng: d : y
x  2 ; d : y
x 1; d : y   1 x   2 ; 1 2 3 3 3  3    3 d : y
x 1. Khẳng định nào đúng trong các khẳng định sau? 4 3
A. d , d , d song song với nhau.
B. d và d song song với nhau. 2 3 4 2 4
C. d và d vuông góc với nhau.
D. d và d song song với nhau. 1 4 2 3 Lời giải Chọn B. 3 3
Các đường thẳng được viết lại như sau: d : y  3x  2 ; d : y
x 1; d : y x 1 ; 1 2 3 3 3 3 d : y x 1. 4 3
 Ta thấy d trùng với d nên loại A và D. 2 3 3
 Đường thẳng d và d có cùng hệ số góc k
và tung độ góc khác nhau nên d và d 2 4 3 2 4 song song với nhau.  2
x  3x  2 x  3
Câu 16. [0D3.2-2] Số nghiệm của phương trình  0 là x 1 A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn A. x  3 ĐKXĐ:   x  3 . x  1 
x  1 l   2
x  3x  2 x  3 2
x  3x  2  0  Phương trình  0    x  2  l  . x 1 x  3  0 
x  3 tm 
Vậy phương trình có nghiệm duy nhất x  3 .
Câu 17. [0D2.3-2] Có bao nhiêu giá trị nguyên của m để đường thẳng y mx  3 không có điểm chung với Parabol 2 y x  1? A. 6 . B. 9 . C. 7 . D. 8 . Lời giải Chọn C.
Phương trình hoành độ giao điểm của đường thẳng y mx  3 và Parabol 2
y x  1 là 2
x 1  mx  3 2
x mx  4  0 .
Điều kiện để đường thẳng y mx  3 không có điểm chung với Parabol 2
y x  1 là phương
trình trên vô nghiệm, hay 2   m 16  0 4   m  4 .
Mà m là số nguyên nên m  3  ; 2  ; 1  ;  0 .
2  x m  x m
Câu 18. [0D3.2-2] Tìm tất cả các giá trị của tham số m để phương trình  0 có x  3 nghiệm
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/21
A. m   ;    1 .
B. m  1;  . C. m  1  ;  .
D. m R . Lời giải Chọn B. ĐKXĐ: x  3  .
2  x m  x m  0  2x m x m  0  x  3m . x  3
Phương trình có nghiệm  3m  3   m  1 .
Câu 19. [0D2.1-1] Chọn khẳng định sai trong các khẳng định sau: A. Hàm số 2 y
x  2x  2 xác định trên R. B. Hàm số 3
y x là hàm số lẻ.
C. Hàm số y   x  2 1 là hàm số chẵn. D. Hàm số 2
y x  1 là hàm số chẵn. Lời giải Chọn C.
Xét hàm số y   x  2
1 có TXĐ: D   .  f  2   2   2 1  9 Ta có   f  2
   f 2 nên hàm số không chẵn.
f 2  2  2 1  1 
Câu 20. [0D3.3-2] Phương trình 3  x  2x  5 có hai nghiệm x , x . Tính x x 1 2 1 2 14 28 7 14 A.  . B.  . C. . D. . 3 3 3 3 Lời giải Chọn D.  8
3  x  2x  5 x  14
Xét phương trình: 3  x  2x  5    
3  x x  .
3  x  5  2x 1 2   3 x  2 
Câu 21. [0H2.2-2] Cho A 3;4 , B  2  ; 
1 , C 0;5 . Tính độ dài trung tuyến AM của ABC . A. 13 . B. 5 . C. 4 . D. 17 . Lời giải Chọn D. Gọi M  ;
x y  là trung điểm BC suy ra M  1  ; 3
AM    2    2 1 3 3 4  17 .
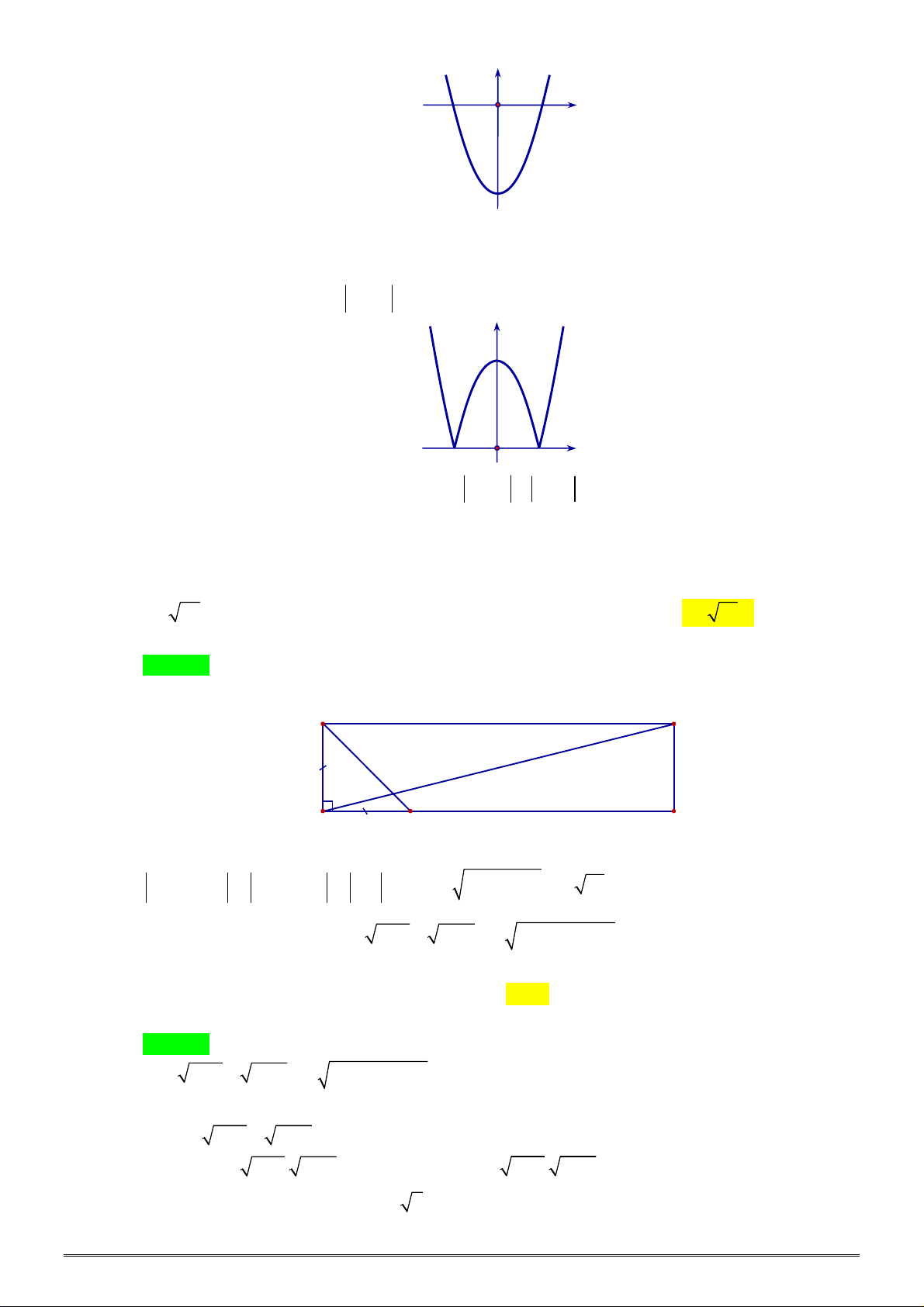
Câu 22. [0D2.3-3] Số giá trị nguyên của m để phương trình 2
x  4  m 1 có bốn nghiệm phân biệt là A. 4 . B. 2 . C. 3 . D. 5 . Lời giải Chọn C. Xét 2
x  4  m 1   1 .
Ta thấy số nghiệm của  
1 là số giao điểm của hai đồ thị 2
y x  4  f x và y m 1. Vẽ đồ thị hàm số 2 y x  4 :
 Vẽ y f x 2  x  4
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/21 y 2  O x 2 4 
 Bằng cách giữ nguyên phần đồ thị của hàm số y f x 2
x  4 phía trên trục hoành và lấy
đối xứng phần đồ thị hàm số y f x 2
x  4 phía dưới trục hoành qua trục hoành, ta được đồ thì hàm số 2
y x  4 như sau: y 4 2  O 2 x
Từ đồ thị, ta thấy để hai đồ thị hàm số 2
y x  4  f x và y m 1 cắt nhau tại bốn điểm
phân biệt  0  m  1  4  1   m  3 .
Do m là số nguyên nên m  0 , m  1, m  2 . Vậy có 3 giá trị m thỏa mãn.  
Câu 23. [0H1.3-2] Cho A
BC vuông cân tại A , AB a . Tính độ dài vectơ AB  4AC . A. 20a . B. 5a . C. 17a . D. 17a . Lời giải Chọn D. Xét hình vẽ sau: B N a 4a A C M  
Dựng AM  4 AC và hình bình hành BAMN như trên, khi đó:     
AB  4 AC AB AM AN AN a   a 2 2 4  a 17 .
Câu 24. [0D3.2-3] Cho phương trình
x 1  5  x  3.  x  
1 5  x  m . Có tất cả bao nhiêu giá trị
nguyên của tham số m để phương trình trên có nghiệm? A. 6 . B. 8 . C. 7 . D. vô số. Lời giải Chọn C.
Xét x 1  5  x  3.  x  
1 5  x  m   1 .
Điều kiện: 1  x  5 . Đặt t
x 1  5  x t  0 . Có 2
t  4  2 x 1. 5  x t  2 và 2
t  4  2 x 1. 5  x  4   x  
1  5  x  8
Do đó, điều kiện của t là 2  t  2 2 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/21 2 t  4 Khi đó   1  t  3.  m  2
3t  2t 12  2m với 2  t  2 2 . 2
Yêu cầu bài toán  Tìm m để hai đồ thị hàm số 2
y  3t  2t 12 với 2  t  2 2 và y  2m có điểm chung.
Bảng biến thiên của hàm số 2
y  3t  2t 12 với 2  t  2 2 t 2 2 2 12  4 2 y 4
Ta thấy rõ ràng trên 2; 2 2  thì 4  y  12  4 2 .  
Nên yêu cầu thỏa mãn khi 4  2m  12  4 2  2  m  6  2 2  8,83 .
Do m là số nguyên nên m 2;3;...; 
8 . Vậy có 7 giá trị m thỏa mãn.
Câu 25. [0D3.2-2] Biết phương trình 4 2 2
x  3mx m 1  0 có bốn nghiệm phân biệt x , x , x , x . 1 2 3 4
Tính M x x x x x x x x . 1 2 3 4 1 2 3 4 A. 2 M m 1. B. M  3  . m C. M  3 . m D. 2
M  m 1. Lời giải Chọn A. Đặt 2
t x  0 suy ra phương trình trở thành 2 2
t  3mt m 1  0 * .
Biết phương trình ban đầu có bốn nghiệm x , x , x , x nên phương trình * có hai nghiệm 1 2 3 4 t t  0 . 1 2
Không mất tính tổng quát giả sử x   t , x   t , x t , x t . 1 1 2 2 3 2 4 1 Khi đó 2
M x x x x x x x x t .t m 1 . 1 2 3 4 1 2 3 4 1 2
Câu 26. [0D2.2-2] Tìm a , b để đồ thị hàm số y ax b đi qua hai điểm A1; 2 , B 3;5 . 7 1 7 1 1 7 1 4 A. a  ,b  .
B. a   ,b   .
C. a   ,b   .
D. a   ,b   . 4 4 4 4 4 4 7 7 Lời giải Chọn B.  7 a   a b  2    4
Vì A1; 2 , B 3;5 nằm trên đồ thị hàm số y ax b nên ta có:    . 3
a b  5 1  b     4
Câu 27. [0D3.2-2] Tìm tất cả các giá trị của tham số m để phương trình  2
m mx  2  mx x  2m
nghiệm đúng với mọi m   . A. m  2 . B. m  2. C. m  1. D. m  1. Lời giải Chọn C. Ta có:  2
m mx   mx x m   2 2 2 m  
1 x  2m  2 . 2 m 1  0
Để phương trình nghiệm đúng với mọi m   thì   m  1 . 2m  2  0 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/21
Câu 28. [0D3.2-2] Biết phương trình 2
x 1  3x  3 
x 1 có hai nghiệm x , x . Tính giá trị biểu 1 2
thức  x 1 . x 1 1   2  A. 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn B.
Điều kiện x  1. 2
x 1  3x  3  x 1 
x 1 1 3  x 1 x 1  x 1  0    x 1  1 3   x  1   x  3  2 3 
Do đó  x 1 . x 1  0 . 1   2 
Câu 29. [0D2.3-3] Xác định hàm số 2
y ax bx c biết đồ thị của hàm số đó cắt trục tung tại điểm có 25 1 tung độ là 3
 và giá trị nhỏ nhất của hàm số là  tại x  . 8 4 1 A. 2
y  2x x  3 . B. 2 y x x  3 . C. 2
y  2x x  3 . D. 2
y  2x x  3 . 2 Lời giải Chọn A.  c  3  c  3  b 1 
Từ giả thiết ta có hệ:    a  2  b 2a 4   2
2b  8ac  25a   25       4a 8 c  3 a  2b  a  2  b  0 loai   c  3    b  1   b  1  2   2b  8 2
b3  252bc  3     a  2bCâu 30. [0D1.3-2] Cho các tập hợp: A  {cam, táo, mít, dừa} ; B  {táo, cam} ;
C  {dừa, ổi, cam, táo, xoài}. Tập  A \ B  C là A. {táo, cam}. B. {mít}. C. {mít, dừa}. D. {dừa}. Lời giải Chọn D.
A \ B   mít, dừa  , suy ra  A \ B  C   dừa  x y  1
Câu 31. [0D3.3-2] Hệ phương trình  có số nghiệm là 2
x  2x  2 y  2  0  A. 1. B. 2 . C. 4 . D. 0 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/21 Lời giải Chọn A. x y  1  y  1 x   y  1 xx  2        . 2
x  2x  2 y  2  0 2 2 
x  2x  2 1 x  2  0 
x  4x  4  0  y  1  
Vậy hệ phương trình có nghiệm duy nhất là 2;  1  .
Câu 32. [0D3.2-2] Tìm tất cả các giá trị của tham số m để phương trình 2
2x  m  2 x m  4  0 có hai nghiệm phân biệt. A. m  6 . B. m  6 . C. m  6 . D. m  . Lời giải Chọn C.
Cách 1. Phương trình có hai nghiệm phân biệt a  0 2  0  2   
m 12m  36  0  m  2 6  0  m  6 .   0 2 
m  4m  4  8m  32  0   x  1 Cách 2. 2
2x  m  2 x m  4  0  
m  4 (do a b c  0 ).  x   2 m  4
Phương trình có hai nghiệm phân biệt   1  m  6 . 2 2 
x xy  2
Câu 33. [0D3.3-3] Hệ phương trình 
có nghiệm là  x ; y thỏa mãn x  1. Tính 0 0  2 2 0
2x xy y  9  x y . 0 0 A. 4 . B. 5 . C. 1. D. 3 . Lời giải Chọn D. 2  2 2
x xy  2 
9x  9xy  18 
9x  9xy  18      2 2
2x xy y  9 2 2 2 2 2 
4x  2xy  2 y  18 
4x  2xy  2 y  9x  9xy  2  2
9x  9xy  18 
9x  9xy  18     2 2
5x 11xy  2 y  0 
 x  2 y  5x y   0  2
x xy  2 2 x  4   x  2  x   x  y    y   y  1    2   2  .   x  2  2
x xy  2 2   4  x  2     loai   y  1  y  5x   y  5x 
Mà x  1 nên x  2 , y  1 . Vậy x y  3 . 0 0 0 0 0      
Câu 34. [0H2.3-3] Cho a b  4 , a  2 , b  3 . Tính a b . A. 3 . B. 10 . C. 12 . D. 2 . Lời giải Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/21 A 4 2 CB 3 C
   
Gọi 3 điểm A , B , C thỏa mãn AB a , BC b .
Suy ra 3 điểm A , B , C lập thành một tam giác với AB  2 , BC  3, CA  4 .     
Ta có a b AB BC AC , với C là điểm đối xứng của C qua B . 2 2 2 AC  AC CC
Áp dụng công thức trung tuyến cho tam giác ACC ta có 2 AB   2 4 2 2 2
4AB CC  2 AC 4.4  36  2.16 Suy ra 2 AC  2  AC   AC  10 . 2 2
Câu 35. [0D1.3-3] Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa.
Biết rằng mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là có 4 bạn thích cả ba môn;
có 9 bạn thích Văn và Sử; có 5 bạn thích Sử và Địa; có 11 bạn thích Văn và Địa; có 24 bạn
thích Văn; có 19 bạn thích Sử và có 22 bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa? A. 21 . B. 23 . C. 24 . D. 22 . Lời giải Chọn D. V S 8 5 9 4 7 1 10 Đ
Gọi V , S , Đ lần lượt là tập hợp các học sinh thích môn Văn, môn Sử và môn Địa.
Ta có biểu đồ Ven thể hiện mối quan hệ giữa các tập hợp trên như hình vẽ.
Suy ra tổng số các học sinh không thích môn Địa là 8  5  9  22 .
Câu 36. [0H2.3-3] Cho M 1;4 , N  1
 ;3 , P 0;6 . Gọi Q a;b là điểm thỏa mãn NPMQ là hình
bình hành. Tổng a b bằng A. 1  . B. 0 . C. 2 . D. 1. Lời giải Chọn D.   Ta có PN   1
 ; 3 và MQ  a 1;b  4 .   a 1  1 a  0
Tứ giác NPMQ là hình bình hành khi và chỉ khi PN MQ     . b  4  3  b  1 
Do đó, a b  1.  
Câu 37. [0H2.3-2] Cho A
BC có AB  5 , A  40 , B  60 . Độ dài BC gần nhất với kết quả nào? A. 3, 7 . B. 3,3 . C. 3,5 . D. 3,1. Lời giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/21 Chọn A.   
Ta có C  180   A B  80 BC AB 5.sin 40 Áp dụng định lí sin:   BC   3, 7 . sin A sin C sin 80  
Câu 38. [0H2.2-2] Cho A
BC đều, AB  6 và M là trung điểm của BC . Tích vô hướng A . B MA bằng A. 1  8 . B. 27 . C. 18 . D. 2  7 . Lời giải Chọn D.    3  Ta có A . B MA A . B M .
A cos150  6.3 3.    27 .  2     
Câu 39. [0H2.2-1] Cho A 0;3 , B 4;0 , C 2; 5   . Tính A . B BC . A. 16 . B. 9 . C. 1  0 . D. 9  . Lời giải Chọn D.  
Ta có AB  4;3 ; BC   6  ; 5     A . B BC  4. 6    3. 5    9  .      1  
Câu 40. [0H2.2-1] Cho hai vectơ a , b khác vectơ 0 thỏa mãn . a b
a . b . Khi đó góc giữa hai 2  
vectơ a , b là A. 60 . B. 120 . C. 150 . D. 30 . Lời giải Chọn A.   1             Ta có . a b
a . b  a ba b 1 . .cos ,  a . b  a b 1 cos , 
 a, b  60 . 2 2 2
Câu 41. [0D2.2-1] Tìm tất cả các giá trị của tham số m để hàm số y  m  
1 .x  2m đồng biến trên . A. m  1. B. m  1. C. m  1. D. m  1. Lời giải Chọn C.
Ta có y  m  
1 .x  2m y   m   1 x  2m .
Hàm số đồng biến trên khi  m  
1  0  m 1  0  m  1 .  
Câu 42. [0H2.2-3] Cho tam giác đều ABC , gọi D là điểm thỏa mãn DC  2BD . Gọi R và r lần lượt R
là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ADC . Tính tỉ số . r 5 5  7 7 7  5 5 7  5 7 A. . B. . C. . D. . 2 9 9 9 Lời giải Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/21 A a B D 2a C 3
Đặt AB BC CA a .        2  2a a
Có DC  2BD  2
DB DC  2DC  2BC DC BC , nên DC  , BD  . 3 3 3
Áp dụng định lý cosin trong tam giác ADC , ta có: 2  2a  2a 2 7a 2 2 2 
AD AC DC  2AC.DC.cos ACD 2  a   2a   cos 60    .  3  3 9 2 7a a 7 Suy ra AD   . 9 3 A . D DC.CA
AD DC CA
Khi đó, tam giác ADC có: S   .r . ADC 4R 2 2 2 2 2 a 3 a 3 Mà SS    . ADC 3 ABC 3 4 6 a 7 2a   a A . D DC.CA a 21 Nên R  3 3   . 4S 2 a 3 9 ADC 4  6 2 a 3 2  2.S a 3 Và ADC r  6   .
AD DC CA a 7 2a 5  7   a 3 3 R a 21 a 3 5 7. 7 7 5 7 Do đó, ta có được:  :   . r 9 5  7 9 9
Câu 43. [0D3.1-2] Phương trình 2 x  2 
x x 1  2x 1
x  2 có số nghiệm là A. 1. B. 3 . C. 2 . D. 0 . Lời giải Chọn D.
Điều kiện xác định: x  2  0  x  2 . 2 x  2 
x x 1  2x 1 x  2 2 
x x 1  2x 1 2x 1  0   
x x 1  2x   2 2 1   1 x    2 2
3x  3x  0 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/21  1 x    2    x  0   x  1 
x  1 (không thỏa mãn điều kiện)
Vậy phương trình cho vô nghiệm. 
Câu 44. [0H2.3-3] Cho A
BC có AB  2 , AC  3 , A  60 . Tính độ dài đường phân giác trong góc
A của tam giác ABC . 12 6 2 6 3 6 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn C. B 2 D A 3 C
Gọi AD là đường phân giác trong của góc A . Ta có SSS ABD ACD ABC 1 A 1 A 1  .A . D A . B sin  .A . D AC.sin  .A . B AC.sin A 2 2 2 2 2 AA . D sin
. AB AC   A . B AC.sin A 2 A . B AC.sin AAD A
AB AC .sin 2 2.3.sin 60 6 3  AD   . 2  3.sin 30 5
Câu 45. [0H2.3-2] Tính diện tích A
BC biết AB  3 , BC  5 , CA  6 . A. 56 . B. 48 . C. 6 . D. 8 . Lời giải Chọn A.
AB BC CA 3  5  6
Nửa chu vi của tam giác ABC là p    7 . 2 2
Áp dụng công thức Hê-rông Sp p a p b
p c  7 7  5.7  67  3  56 (đvdt). ABC    
Câu 46. [0H2.3-2] Cho A
BC có AB  3 , BC  5 và độ dài trung tuyến BM  13 . Tính độ dài AC . 9 A. 11 . B. 4 . C. . D. 10 . 2 Lời giải Chọn B.
Áp dụng công thức tính độ dài đường trung tuyến ta có
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/21 2 2 2 BA BC AC 2 BM   2  AC   2 2 BA BC  2 2  4BM 2  AC   2 2 2 3  5   4.13 2 4 2
AC  16  AC  4 .
Câu 47. [0H2.3-2] Cho A
BC vuông ở A , biết 
C  30 , AB  3 . Tính độ dài trung tuyến AM . 5 7 A. 3 . B. 4 . C. . D. . 2 2 Lời giải Chọn A. A 3 30 B M C AB Do tam giác A
BC vuông ở A , C  30 , AB  3 nên BC   6 . sin 30 1
Độ dài đường trung tuyến AM BC  3 . 2
Câu 48. [0D3.2-2] Tìm tất cả các giá trị của tham số m để phương trình m   2 x   2 1 m   1 x  3  0 có hai nghiệm trái dấu. A. m  1. B. m  0 . C. m  0 . D. m  1. Lời giải Chọn A.
Phương trình m   2 x   2 1 m  
1 x  3  0 có hai nghiệm trai dấu khi và chỉ khi m 1  0  m  1     m  1 .  3  m   1  0  m  1 
Vậy m  1 thì phương trình đã cho có hai nghiệm trái dấu. 2
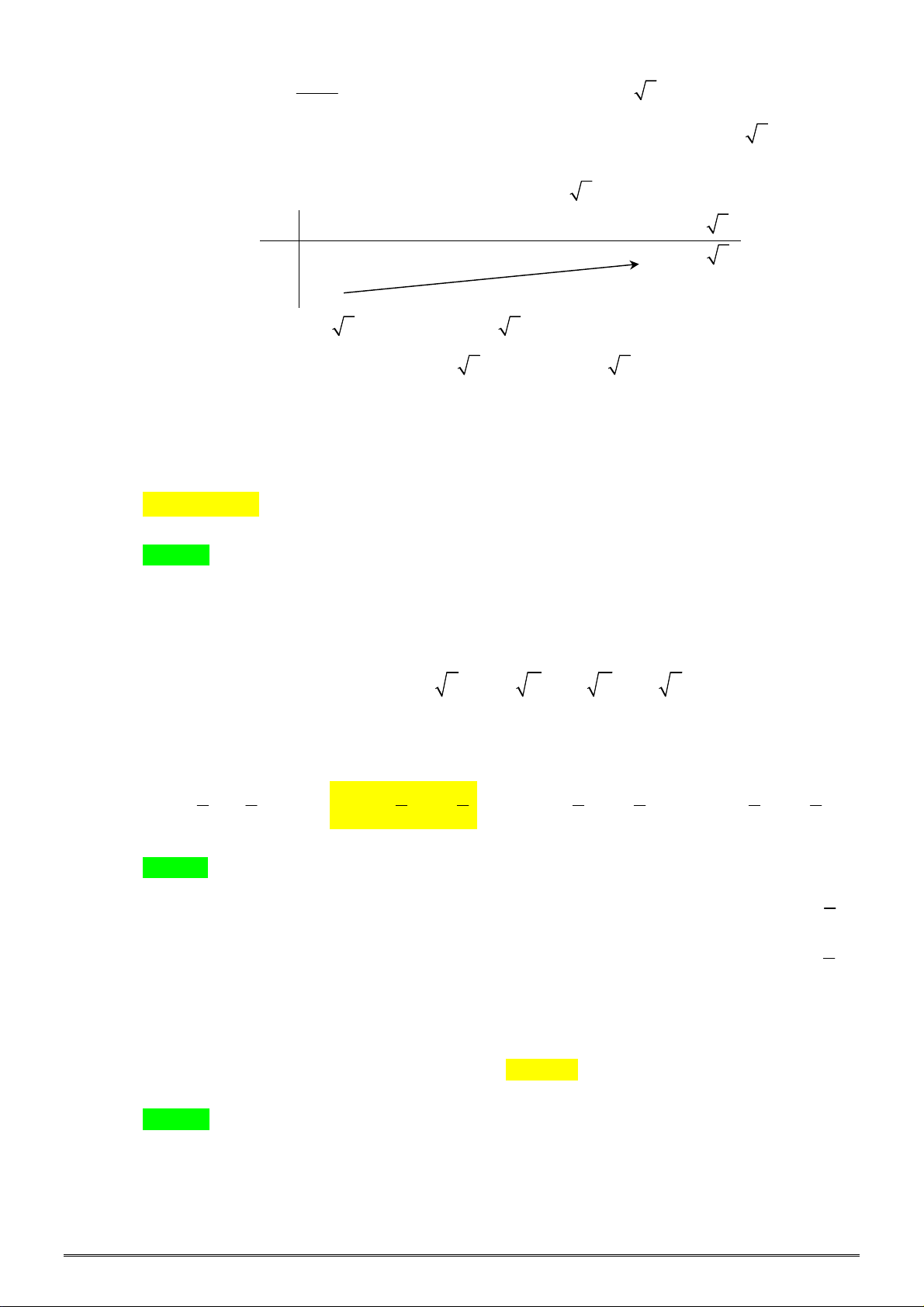
x  2x  8 khi x  2
Câu 49. [0D2.3-3] Cho hàm số y  
. Gọi M , m lần lượt là giá trị lớn nhất và 2x 12 khi x  2 
giá trị nhỏ nhất của hàm số khi x 1;4 . Tính M m . A. 1  4 . B. 1  3 . C. 4  . D. 9  . Lời giải Chọn B.
Ta có đồ thị của hàm số khi x 1;4 như hình vẽ dưới đây: y 1  4 x O 4  5  8  9 
Dựa vào đồ thị ta có M  4
 , m  9  M m  1  3 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/21
y  2x  4xy y
Câu 50. [0D3.3-3] Biết hệ phương trình 
có nghiệm  x ; y với x  0 . Tỉ số 0 bằng 0 0 
2 y x  3xy 0  x0 1 A. 2 . B. . C. 1  . D. 1. 2 Lời giải Chọn A.
y  2x  4xy
3y  6x  12xy
y  2x  4xy
y  2x  4xy Ta có:       
2 y x  3xy
8 y  4x  12xy
5y  10x  0  y  2x  x  0  y  0 
2x  2x  4 . x 2x 2 4x  8x       1 . y  2xy  2x  x   2  y  1  y
Vì x  0 nên tỉ số 0  2 . 0 x0
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/21
Document Outline

  • [toanmath.com] - Đề thi học kỳ 1 Toán 10 năm học 2018 – 2019 trường Lương Thế Vinh – Hà Nội.pdf
  • 003-TOAN 10-HKI-1819-LUONG THE VINH-HNO-1819.pdf