Đề Thi Học Kỳ 1 Toán 9 Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I QUẢNG NAM
Môn: TOÁN – LỚP 9
Thời gian: 90 phút (không kể thời gian giao đề) ĐỀ CHÍ NH THỨC
Bài 1 (2,0 điểm):
a) Với giá trị nào của x thì 6 + x xác định? b) Thực hiện tính: 1 A = 60 : 15 ; B = 2 (2 − 5) + 4 ; C = + 2 2 + 3
Bài 2 (1,5 điểm):  1 1  a + 2 a +1 Cho biểu thức P = − .  
với a  0 và a  1.
 a +1 a + a  a −1
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi a = 2 3 − 5 (3+ 5)( 10 − 2).
Bài 3 (2,0 điểm):
a) Tìm điều kiện của m để hàm số y = (m − 3)x + 4 là hàm số bậc nhất.
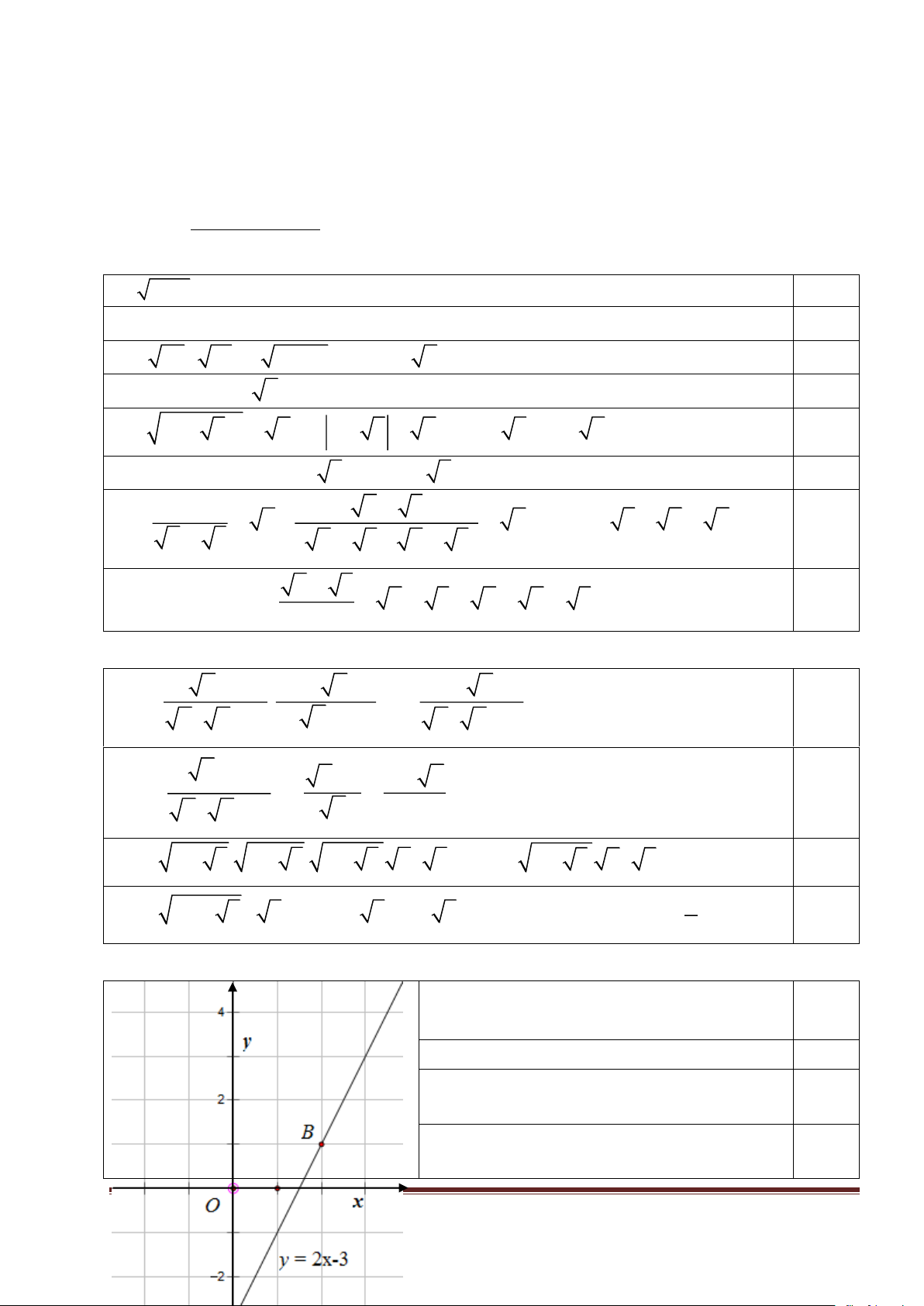
b) Vẽ đồ thị hàm số y = 2x − 3
c) Tìm m để đồ thị hàm số y = (m − 3)x + 4 cắt đồ thị hàm số y = 2x − 3 tại
điểm có hoành độ bằng 1.
Bài 4 (2,0 điểm):
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.
a) Tính độ dài đoạn thẳng AH.
b) Tính các tỉ số lượng giác: tanB , sin C .
c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC. Chứng minh AE.AB = AF.AC
Bài 5 (2,5 điểm):
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi
M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thẳng qua M vuông
góc với OM cắt Ax tại C và cắt By tại D. a) Chứng minh CA = CM.
b) Chứng minh MOB = 2. MAO , từ đó suy ra AM song song với OD.
c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông
góc với đường thẳng AB. Trang 1 ===== HẾT =====
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I QUẢNG NAM
HƯỚNG DẪN CHẤM MÔN TOÁN 9 Bài 1 (2,0 điểm):
a) 6 + x xác định khi 6 + x ≥ 0 0,25  x ≥ −6 0,25
A= 60 : 15 = 60 :15 (hoặc = 4 ) 0,25 = 4 = 2 0,25 B = 2
(2 − 5) + 4 = 2 − 5 + 4 (hoặc 5 − 2 + 4 ) 0,25 = 5 − 2 + 2 = 5 0,25 1 2 − 3 C = + 2 = + 2 (hoặc = 3 − 2 + 2 ) 2 + 3 ( 0,25 2 + 3)( 2 − 3) 2 − 3 = + 2 = 3 − 2 + 2 = 3 0,25 2 − 3
Bài 2 (1,5 điểm): a −1 a + 2 a +1 a + 2 a +1 P = = 0,50 a ( a + ). 1 a −1 a ( a + ) 1 ( a + )2 1
a +1 a + a = = = 0,50 a ( a + ) 1 a a
a = 2 3 − 5. 3 + 5. 3 + 5. 2 ( 5 − ) 1 = 4 3 + 5. 2 ( 5 − ) 1 0,25 5 a = 4 6 + 2 5.( 5 − ) 1 = 4( 5 + ) 1 ( 5 − ) 1 =16 . Tính được P = 0,25 4
Bài 3 (2,0 điểm):
Để y = (m − 3)x + 4 là hàm số bậc nhất 0,25 thì m − 3  0  m  3 0,25
Xác định được tọa độ hai điểm thuộc đồ 0,50
thị hàm số (Ví dụ: A(0; -3) và B(2;1)).
Vẽ đồ thị hàm số y = 2x-3:
- Vẽ hệ trục tọa độ. Trang 2
- Biểu diễn hai điểm trên hệ trục tọa độ. 0,25
- Vẽ đường thẳng qua hai điểm. 0,25
Gọi C(x0; y0) là tọa độ giao điểm. Có: x0 =1  y = 2.1− 3 = 1 − 0,25 0
y = (m − 3)x + 4 qua C(1; -1) có: 0,25 1
− = m − 3 + 4  m = − 2. Bài 4 (2,0 điểm):
Hình vẽ: phục vụ câu a), b) 0,25 B phục vụ câu c) 0,25 Có: 1 1 1 1 1 1 = + thay: = + 2 2 2 2 2 2 0,25 E H AH AB AC AH 4 5 2 2 4 .5 20 2 AH =  AH= (3.12) 0,25 2 2 4 +5 41 AC 5 tanB = = ( = 1.25 ) 0,25 C F AB 4 A AH 20 4 sinC = = :5 = (  0.62 ) 0,25 AC 41 41
AHB vuông tại H có HE là đường cao nên AE. AB = AH2 0,25
Tương tự có AF.AC = AH2  AE. AB = AF.AC (cùng bằng AH2) 0,25 Bài 5 (2,5 điểm):
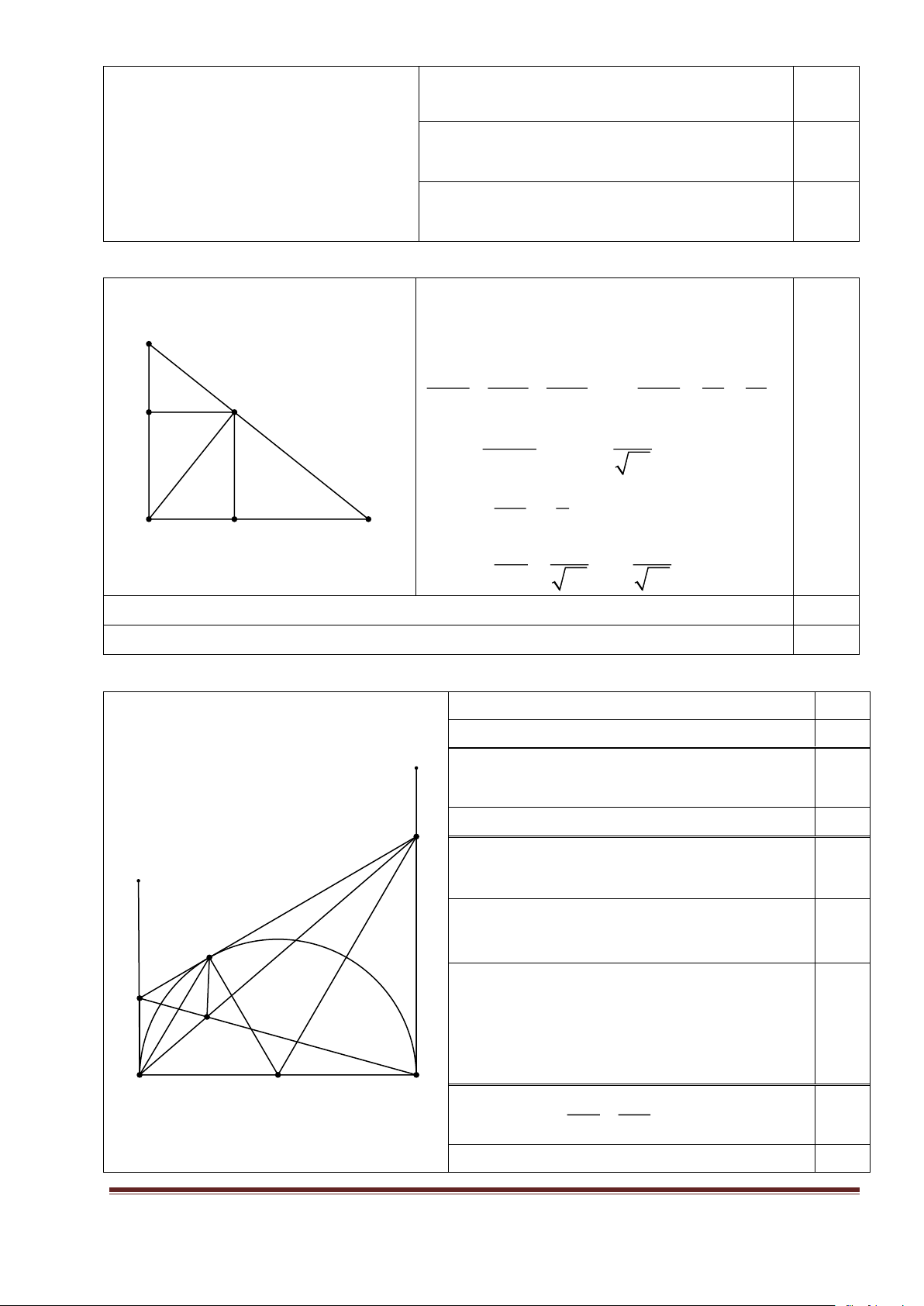
Hình vẽ: phục vụ câu a) 0,25
Chỉ yêu cầu phục vụ câu b) 0,25
y CM ⊥ MO  CM là tiếp tuyến của (O) 0,25
CA ⊥ AO  CA là tiếp tuyến của (O). 0,25 D
 CM = CA (T.chất 2 tt cắt nhau). 0,25
OMA cân tại O do OM = OA 0,25 x  MAO = AMO
Mà MOB = MAO + AMO (góc ngoài) M 0,25  MOB = 2 MAO
Lí luận được BD là tiếp tuyến của (O) C
 OD là phân giác của MOB N 0,25  MOB = 2 DOB  MAO = DOB  AM // OD A O B NC AC AC// BD  = 0,25 NB BD Mà AC= MC và BD = MD 0,25 Trang 3  NC MC =  MN//BD MN ⊥ AB NB MD
Học sinh giải cách khác đúng, tổ chấm thảo luận, thống nhất cho điểm phù hợp. ===== HẾT==== Trang 4