Đề thi học sinh giỏi cấp tỉnh Toán 11 năm 2023 – 2024 sở GD&ĐT Thái Nguyên

UBND TỈNH THÁI NGUYÊN
THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 11
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024 MÔN THI: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài:150 phút, không kể thời gian phát đề
Bài 1 (5 điểm). a. Giải phương trình 2
sin 5x  2 sin x  1 .
b. Cho cấp số nhân (u ) với số hạng đầu u  3 và công bội q  2;1 n 1   . Tính giá trị 1
của biểu thức S  u  87u  2q khi u  u 
u đạt giá trị lớn nhất. 11 3 1 2 3 3
Bài 2 (4 điểm). a. Tính lim   .   3 3 2 2x 8x x x  2 2 2 b. Giải phương trình x 4 x3 x 7 x6 2 x 3x    9 2024 2024 2024 1.
Bài 3 (2 điểm). Cho tập hợp A  1; 2; 3; 4; 
5 . Gọi B là tập hợp gồm tất cả các số tự nhiên
có ít nhất ba chữ số, các chữ số đôi một khác nhau thuộc tập hợp .
A Chọn ngẫu nhiên một
số thuộc tập hợp B. Tính xác suất để số được chọn có tổng các chữ số bằng 10.
Bài 4 (2 điểm). Cho tam giác ABC có đỉnh (
A 1; 2), đường trung tuyến BM có phương
trình 2x  y  1  0 và đường phân giác trong CD có phương trình x  y 1  0 . Viết
phương trình đường thẳng BC .
Bài 5 (4 điểm). Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Điểm M di
động trên cạnh SC ( M  S và M  C ), ( ) là mặt phẳng qua AM và song song với B . D
a. Tìm các giao tuyến của mặt phẳng ( ) với các mặt phẳng ( ABCD) , (SBD).
b. Gọi H và K lần lượt là giao điểm của mặt phẳng ( ) với SB và SD . Chứng minh SB SD SC rằng  
có giá trị không đổi. SH SK SM
Bài 6 (1 điểm). Tìm tất cả các hàm số f :    thỏa mãn:
f  xf (x)  f ( y   f  2 )
f (x )  y với mọi số thực x,y.
Bài 7 (2 điểm). Một câu lạc bộ có 41 thành viên, mỗi người quen với ít nhất 21 người khác
(trong đó quan hệ quen biết là hai chiều).
a. Chứng minh rằng tồn tại 3 thành viên đôi một quen nhau.
b. Chứng minh rằng tồn tại ít nhất một thành viên có số người quen là số chẵn.
c. Hỏi có thể xảy ra trường hợp 3 thành viên bất kỳ trong câu lạc bộ đều có không
quá 5 người quen chung hay không?
-------- Hết --------
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên.......................................................................................SBD........................ UBND TỈNH THÁI NGUYÊN
THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 11
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024 MÔN THI: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài:150 phút, không kể thời gian phát đề
HƯỚNG DẪN CHẤM ĐỀ THI MÔN TOÁN
I. Hướng dẫn chung
1) Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số
điểm từng phần như hướng dẫn quy định.
2) Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải bảo đảm không làm sai
lệch hướng dẫn chấm và phải được thống nhất thực hiện trong tổ chấm.
II. Đáp án và thang điểm Bài Nội dung Điểm a. Giải phương trình 2
sin 5x  2sin x  1. 3.0 2
sin 5x  2sin x  1 0.5
 sin 5x   cos 2x   
 sin 5x  sin 2x    0.5  2    5x  2x   k 2  2   0.5 
5x    2x   k2  2   3x    k 2  2 Bài 1   0.5 3 (5đ)  7x   k 2  2   k 2 x     6 3   k  . 0.5 3 k 2  x    14 7
Phương trình đã cho có các nghiệm là:  k 2 3 k 2 0.5 x    , x   k  . 6 3 14 7
b. Cho cấp số nhân (u ) với số hạng đầu u  3 và công bội q  2   ;1 . n 1 1
Tính giá trị của biểu thức S  u  87u  2q khi u  u  u đạt giá trị 11 3 1 2 3 2.0 3 lớn nhất. 2 2 1 1  3  3 Ta có 2 2
u  u  u  u  u q  u q  q  3q  3  q   . 0.5 1 2 3 1 1 1   3 3  2  4 2 7 3 1 1  3  49 Do q  2   ;1    q      q     . 2 2 2 4  2  4 0.5 2  3  3  1  q    13.    2  4 1
 u  u  u  13 . 1 2 3 3
Dấu đẳng thức xảy ra khi q  2  . 0.5 1
Vậy giá trị lớn nhất của u  u  u bằng 13. 1 2 3 3 Suy ra 10 2
S  u  87u  2q  u q  87u q  2q 11 3 1 1 0.5 10 2  3( 2) 
 87.3.(2)  2(2)  2024 a. Tính lim   . 2.0   3 3 2 2x 8x x x  3 3 2 2x  8x  x lim    0.5   3 3 2 2x 8x x      lim x x 3
4x  2x 8x  x   3 8x  x 2 2 3 2 3 2 2 x  lim x 2 1  1 0.5 2 2 2  3 3 4x  2x 8   x 8    x  x  1   l m i x 2 1  1  0.5 3 3 4  2 8   8    x  x  Bài 2 1  1 (4 đ)    . 0.5 4  4  4 12 2 2 2 b. Giải phương trình x 4 x3 x 7 x6 2 x 3 x9 2024  2024  2024 1. 2.0 2 2 2 x 4 x3 x 7 x6 2 x 3x9 2024  2024  2024 1 0.5 2 2 2 2 x 4 x3 x 7 x6 x 4 x3 x 7 x6  2024  2024  2024 .2024 1   2 x  x   2 x  x   2 4 3 7 6 x 4 x3 2024 1 2024 1 2024   0 0.5   2 x  x   2 4 3 x 7 x6 2024 1 1 2024   0 2 x 4 x3 2024 1  0   2 x 7 x6 1   2024  0  0.5 2
x  4x  3  0   2
x  7x  6  0  3  x  1  x  3   .  x  1  0.5  x  6  
Vậy phương trình đã cho có tập nghiệm là S   6  ; 1; 1;  3 .
Cho tập hợp A  1; 2; 3; 4; 
5 . Gọi B là tập hợp gồm tất cả các số tự
nhiên có ít nhất ba chữ số, các chữ số đôi một khác nhau thuộc tập hợp 2.0 .
A Chọn ngẫu nhiên một số thuộc tập hợp .
B Tính xác suất để số được
chọn có tổng các chữ số bằng 10.
Số các số tự nhiên có 3 chữ số, các chữ số đôi một khác nhau thuộc tập 0.25 hợp A là: 3 A  60. 5
Số các số tự nhiên có 4 chữ số, các chữ số đôi một khác nhau thuộc tập 0.25 hợp A là: 4 A  120. 5
Số các số tự nhiên có 5 chữ số, các chữ số đôi một khác nhau thuộc tập Bài 3 0.25 hợp A là: 5 A  120. 5 (2đ)
Vậy B  60 120 120  300. 0.25
Các tập con của tập hợp A có tổng của các phần tử bằng 10 là:
A  1; 2; 3; 4 ; A  2; 3; 5 ; A  1; 4; 5 . 0.25 1   2   3  
Số các số tự nhiên thuộc tập hợp B có tổng các chữ số bằng 10 là: 0.25 4! 3! 3!  36.
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”.
Vậy xác suất để số được chọn có tổng các chữ số bằng 10 là: X 36 3 0.5 P( X )    .  300 25
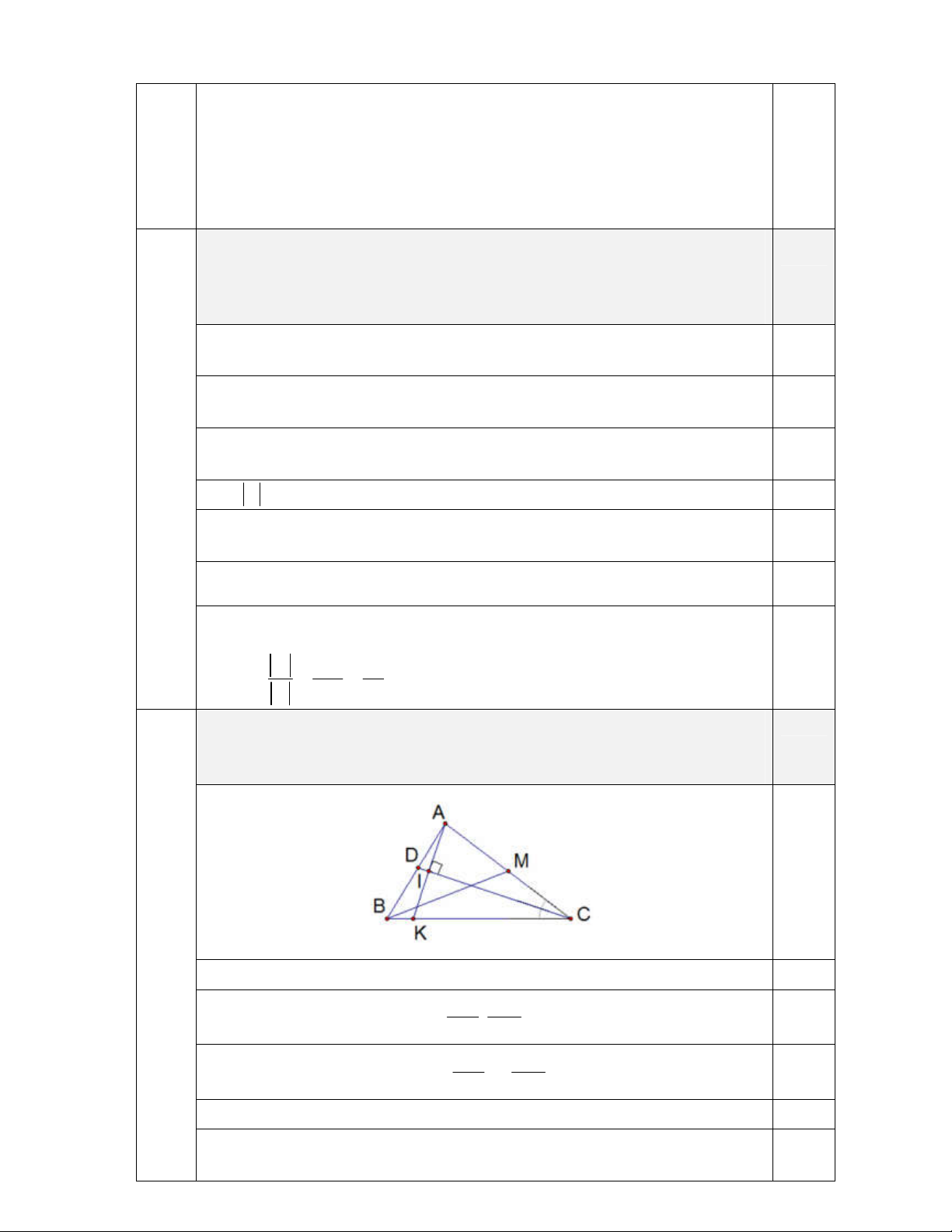
Cho tam giác ABC có đỉnh (
A 1; 2), đường trung tuyến BM có phương
trình 2x  y 1  0 và đường phân giác trong CD có phương trình 2.0
x  y 1  0 . Viết phương trình đường thẳng BC . Bài 4 (2đ)
Điểm C  CD : x  y 1  0  C t;1 t . 0.25
 t 1 3  t 
Trung điểm M của AC là M ;   . 0.25  2 2   t 1  3  t
Điểm M thuộc BM , suy ra: 2  1  0.   0.25  2  2 Hay t  7   C  7  ;8 0.25
Từ A1;2 kẻ AK vuông góc với CD tại I (điểm K  BC ). Suy ra 0.25
AK có phương trình: 4  x  
1   y  2  0  x  y 1  0.
x  y 1  0
Toạ độ I thoả mãn hệ:   I 0;  1 . 0.25
x  y 1  0 
Tam giác ACK cân tại C nên I là trung điểm AK , suy ra toạ độ của K  1  ;0 . 0.25
Đường thẳng BC đi qua C và K nên có phương trình: x 1 y 0.25 
 4x  3y  4  0. 7  1 8
Cho hình chóp S.ABCD có đáy là hình bình hành. Điểm M di động
trên cạnh SC ( M  S và M  C ), ( ) là mặt phẳng qua AM và song song với . BD 2.0
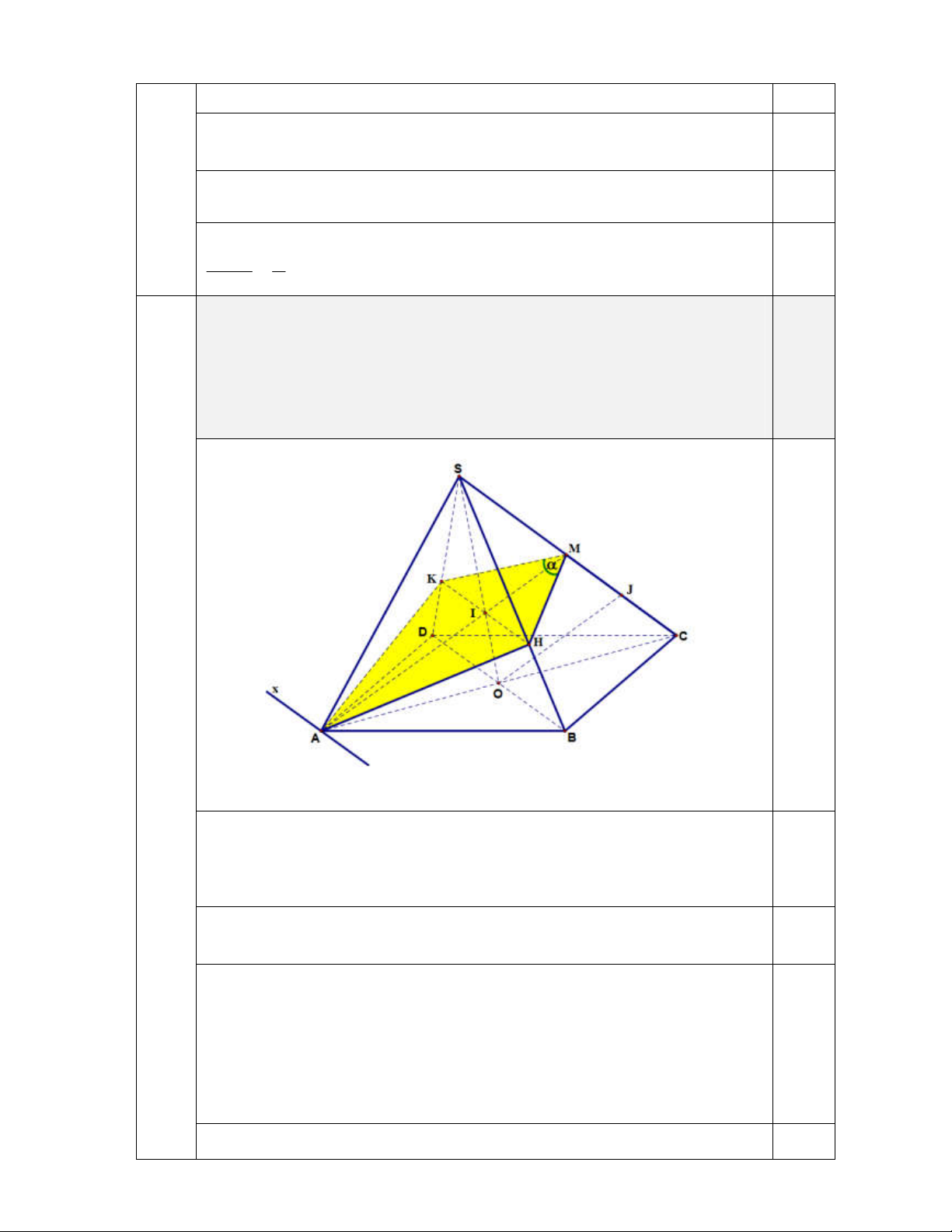
a. Tìm các giao tuyến của mặt phẳng ( ) với các mặt phẳng ( ABCD) , (SBD). Bài 5 (4đ)
Chú ý: Không có hình vẽ thì không cho điểm cả bài
 A   ABCD    
Ta có:  BD   ABCD . 0.5  BD    
Suy ra  ABCD     Ax , với Ax là đường thẳng đi qua A và song 0.5 song với BD .
Trong mặt phẳng  SAC  , gọi I là giao điểm của SO và AM . Gọi J là
trung điểm của MC , khi đó AM  OJ .
I  SBD    0.5  BD   SBD  BD    
Suy ra  SBD     Iz , với Iz là đường thẳng qua I và song song với BD . 0.5 5
b. Gọi H và K lần lượt là giao điểm của mặt phẳng ( ) với SB và S . D SB SD SC 2.0 Chứng minh rằng  
có giá trị không đổi. SH SK SM
Ta có H  Iz  SB, K  Iz  . SD
Do đó KH  BD,OJ  AM nên theo định lý Ta-let, ta có: 0.5 SB SD SO   . SH SK SI Vậy: SB SD SC SO SC 0.25    2  SH SK SM SI SM SJ SC  2  0.25 SM SM
2SM  MJ   SC  0.25 SM
2SM  MJ   SM  MJ  JC   0.25 SM
SM  MJ  JC  0.25 SM SM  SM  1. 0.25 SB SD SC Như thế  
có giá trị không đổi. SH SK SM
Tìm tất cả các hàm số f :    thỏa mãn: 1.0
f  xf (x)  f ( y   f  2 )
f (x )  y với mọi số thực x, y.
Giả sử tồn tại hàm số f :    thoả mãn
f  xf x  f y   f  2 ( ) ( )
f (x )  y,  x, y  .    1
Bài 6 Giả sử tồn tại các số thực a,b sao cho f a  f b  M. Từ   1 lần
(1đ) lượt cho y  a, y  b ta được: 0.25
 f xf x  M   f 
 f  2x  a   a  b .
 f  xf  x  M   f  f  2 x   b 
Vậy f là đơn ánh. 6 Từ  
1 cho x  1, y  0 ta được f  f  
1  f 0  f  f   1   f  
1  f 0  f  
1  f 0  0 .
Thay y  0 vào   1 ta được
f  xf  x  f  f  2
x   xf  x  f  2 x , x   .  2 0.25
Thay x  0 vào   1 ta được
f  f  y  y, y   .  3 Từ   1 và 3 suy ra
f  xf  x  f  y 2  x  y, x  , y .  4
Từ 4 cho y  0 ta được
f  xf  x 2  x , x    5
Từ 5 thay x bởi f  x và chú ý đến 3 ta được 0.25
f  xf  x  f  x2 , x    6
Từ 5 và 6 suy ra f  x2 2  x , x    7
(nghĩa là với x   thì f  x  x hoặc f  x  x )
Giả sử tồn tại x  0, y  0 sao cho f  x  x và f  y   y . Từ 4 0  0  0 0 0 0
cho x  x , y  y ta được 0 0   2 2
7  x  y  x  y  y  0 f  2 x  y  x  y   ; 0 0  2 0 0 0 0 0 0 0  2 2 
x  y  x  y x  0  0 0 0 0  0
mâu thuẫn với x  0, y  0 . 0 0   f  x  x 0 
Như vậy với mọi x  0, y  0 thì theo 7 ta có 0 hoặc 0.25 0 0  f   y  y  0  0   f  x  x 0  0  . f   y   y  0  0
Do đó f  x  x, x
   (thử lại đúng) hoặc f  x  x, x    (thử
lại đúng). Vậy các hàm số thoả mãn yêu cầu đề bài gồm
f  x  x, x
  ; f  x  x, x   . 
Một câu lạc bộ có 41 thành viên, mỗi người quen với ít nhất 21 người
khác (trong đó quan hệ quen biết là hai chiều). 1.0
a. Chứng minh rằng tồn tại 3 thành viên đôi một quen nhau.
Xét hai người a,b quen nhau và gọi A là tập hợp người quen của a, Bài 7
(2đ) không tính b ; gọi B là tập hợp người quen của b, không tính . a
Theo giả thiết thì A  20, B  20 , mặt khác A  B  41 2  39 nên rõ 0.5 ràng
A  B  A  B  A  B  0 . 7
Điều này chứng tỏ a,b có người quen chung, đặt là . c 0.5 Suy ra a, ,
b c đôi một quen nhau.
b. Chứng minh rằng tồn tại ít nhất một thành viên có số người quen là số chẵn. 0.5
Gọi x , x ,, x là số người quen của các thành viên thứ 1, 2,, 41. 1 2 41
Ta thấy rằng x  x   x chính là tổng số lượt quen nhau của tất cả 1 2 41 các thành viên.
Mặt khác, mỗi cặp quen nhau thì đóng góp 2 đơn vị vào tổng đó (do 0.5
người này tính người kia là người quen, và ngược lại) nên tổng số lượt
quen nhau phải luôn chẵn.
Từ đó suy ra trong 41 số x ở trên, phải có ít nhất một số chẵn. i
c. Hỏi có thể xảy ra trường hợp 3 thành viên bất kỳ trong câu lạc bộ đều 0.5
có không quá 5 người quen chung hay không?
Giả sử rằng khẳng định là đúng.
Ta đếm số lượng S gồm các bộ ({a , a , a },b) sao cho thành viên 1 2 3
a , a , a cùng quen . b 1 2 3 Đếm theo ,
b ta thấy mỗi thành viên quen ít nhất 21 người nên 0.25 3 S  41 C . 21
Đếm theo {a , a , a }, theo giả sử ở trên thì mỗi bộ ba có không quá 5 1 2 3 người quen chung nên 3 S  5  C . 41 Từ đó ta có 3 3
41 C  5  C  41 21 20 19  5  41 40  39  2119  10  39. 21 41
Bất đẳng thức cuối là sai nên điều giả sử ban đầu cũng sai. Do đó, không 0.25
thể xảy ra trường hợp 3 thành viên bất kỳ trong câu lạc bộ đều có không quá 5 người quen chung.
……….HẾT……….
Document Outline

• DE TOAN_LOP 11_2023_2024
• DAP AN_TOAN_11_2023_2024