
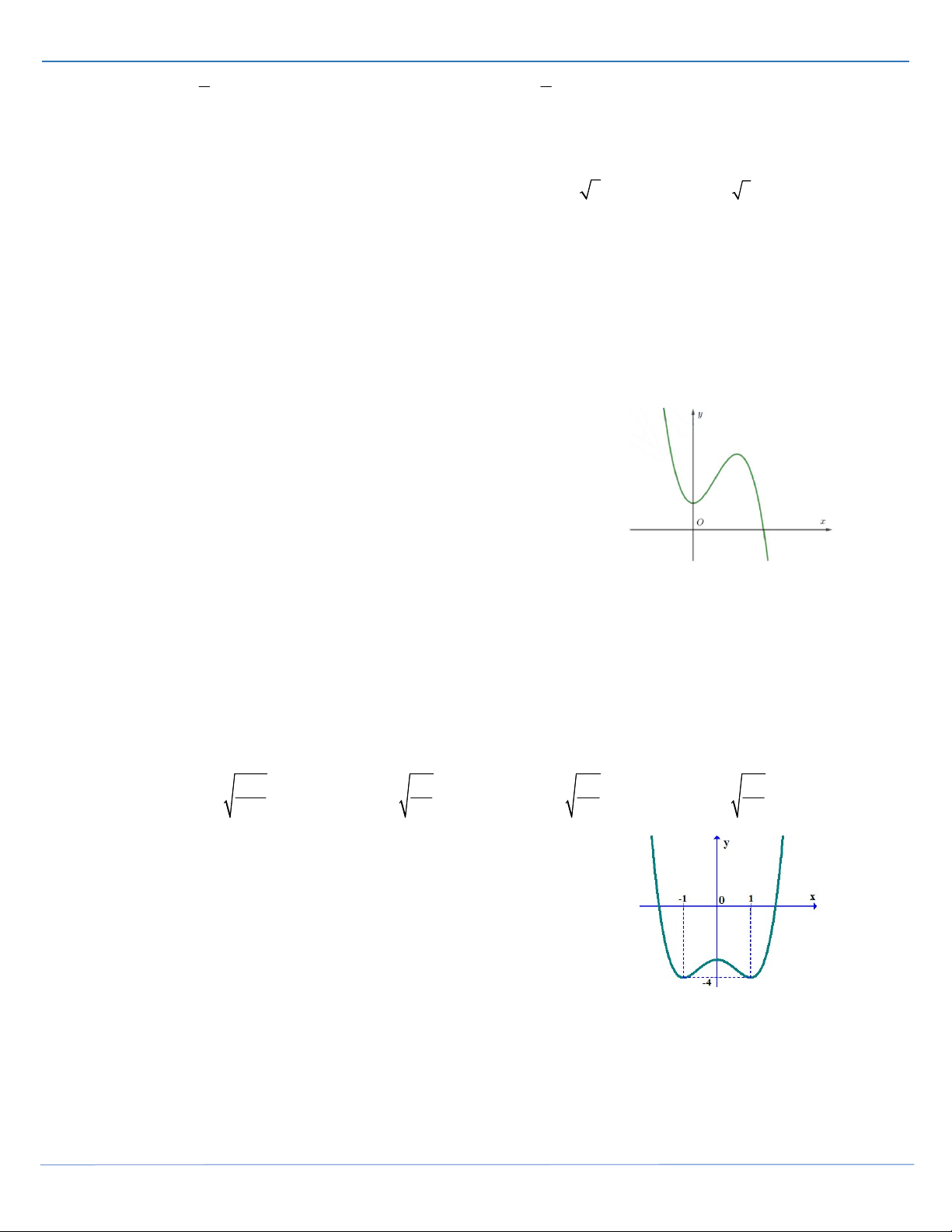














Preview text:
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC 2021 - 2022 Môn thi: TOÁN - THPT
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Đề thi gồm 06 trang - 50 câu trắc nghiệm MÃ ĐỀ: 106 x
Câu 1: Cho F x là một nguyên hàm của hàm số f x
thỏa mãn F 2 0 . Tính số 2 8 x
nghiệm phương trình F x x . A. 2 . B. 0 . C. 3 . D. 1.
Câu 2: tập xác định của hàm số y log 2 x 7x 10 là 2 A. ; 25; . B. 2;5.
C. ;2 5; . D. 2;5 .
Câu 3: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2 021;202 1 để hàm số 1 y ln 2
x 4 mx 2 nghịch biến trên khoảng ; ? 2 A. 2022. B. 2019. C. 2021. D. 2020.
Câu 4: Cho hàm số f x có đạo hàm f x x 2 x 4 1 3 x 1 , x
. Số điểm cực trị của hàm số y f x là A. 3. B. 2. C. 1. D. 4.
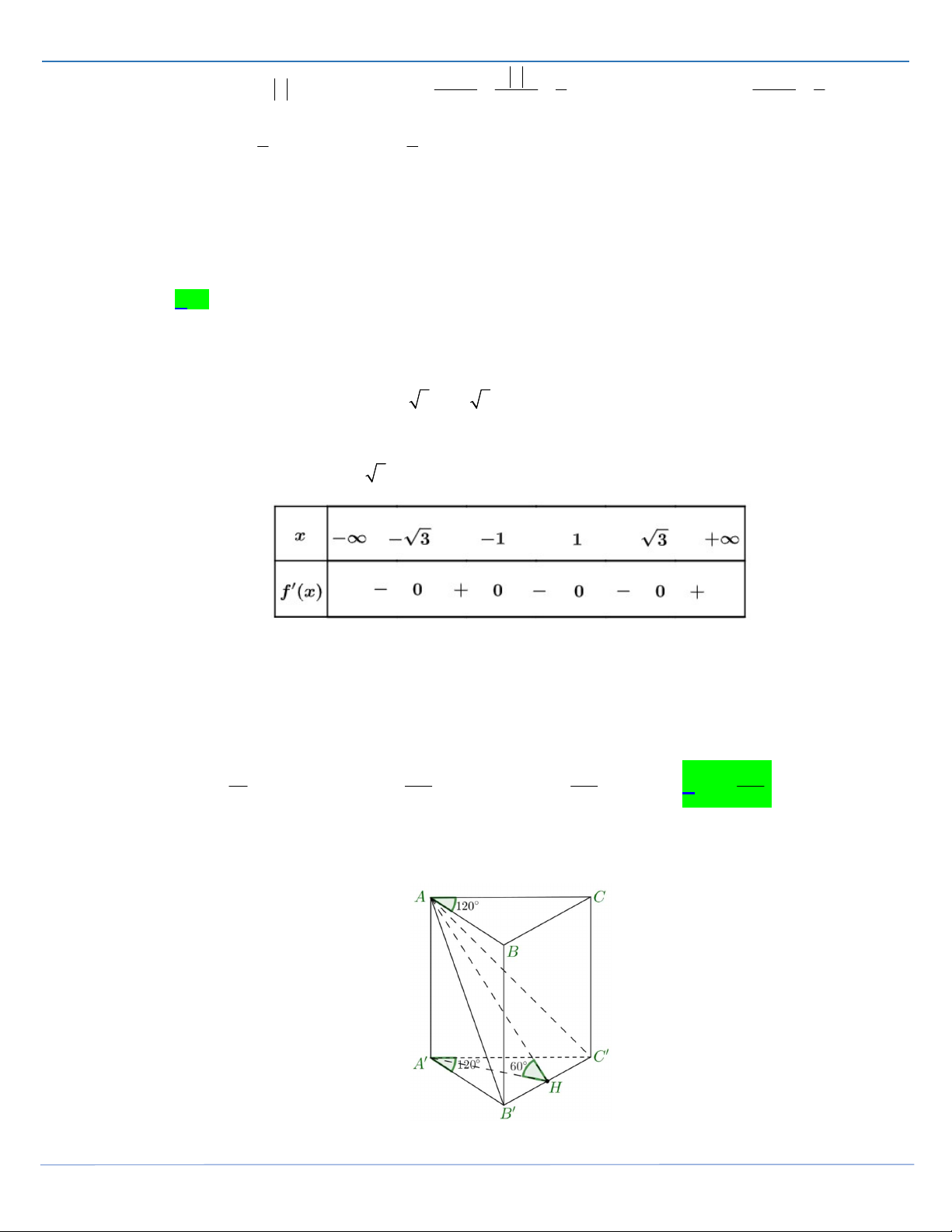
Câu 5: Cho khối lăng trụ đứng ABC.AB C
có đáy ABC là tam giác cân với AB AC a , 0
BAC 120 . Mặt phẳng AB C
tạo với đáy một góc 0
60 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 3a 3 9a 3 3a A. V . B. V . C. V . D. V . 8 4 8 8
Câu 6: Cho hàm số y f x , biết f 3 0 và 2 . x f x
x e , x . Tính tích phân 2 1 I xf xd .x 0 e 3 e 1 e 1 e 2 A. I . B. I . C. I . D. I . 4 4 2 4
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB 2a . Tam giác SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC . 3 a 3 3 4a 3 3 2a 3 3 a 3 A. . B. . C. . D. . 3 3 3 12 Câu 8: Cho mặt cầu 1
S có bán kính là a , mặt cầu S2 có bán kính là 2a . Tỷ số diện tích của mặt cầu 1
S và mặt cầu S2 bằng
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 1
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 1 1 A. . B. 4 . C. . D. 2 . 2 4
Câu 9: Cho hình đa diện đều loại 4;
3 có cạnh bằng a . Gọi S là tổng diện tích tất cả các mặt của
hình đa diện đó. Mệnh đề nào sau đây là đúng? A. 2 S 4a . B. 2 S 6a . C. 2 S 2 3a . D. 2 S 3a .
Câu 10: Tập giá trị của hàm số y 2sin 2x 3 là A. 2; 2 . B. 1;5 C. 2;5. D. 1; 2 .
Câu 11: Số cách xếp 5 người ngồi vào một hàng ghế dài là A. 130 . B. 100 . C. 125 . D. 120 .
Câu 12: Cho cấp số cộng u thỏa mãn u 3 và u 18 . Số hạng u bằng n 1 6 10 A. 27 . B. 30 . C. 2 4. D. 21. Câu 13: Cho hàm số 3 2
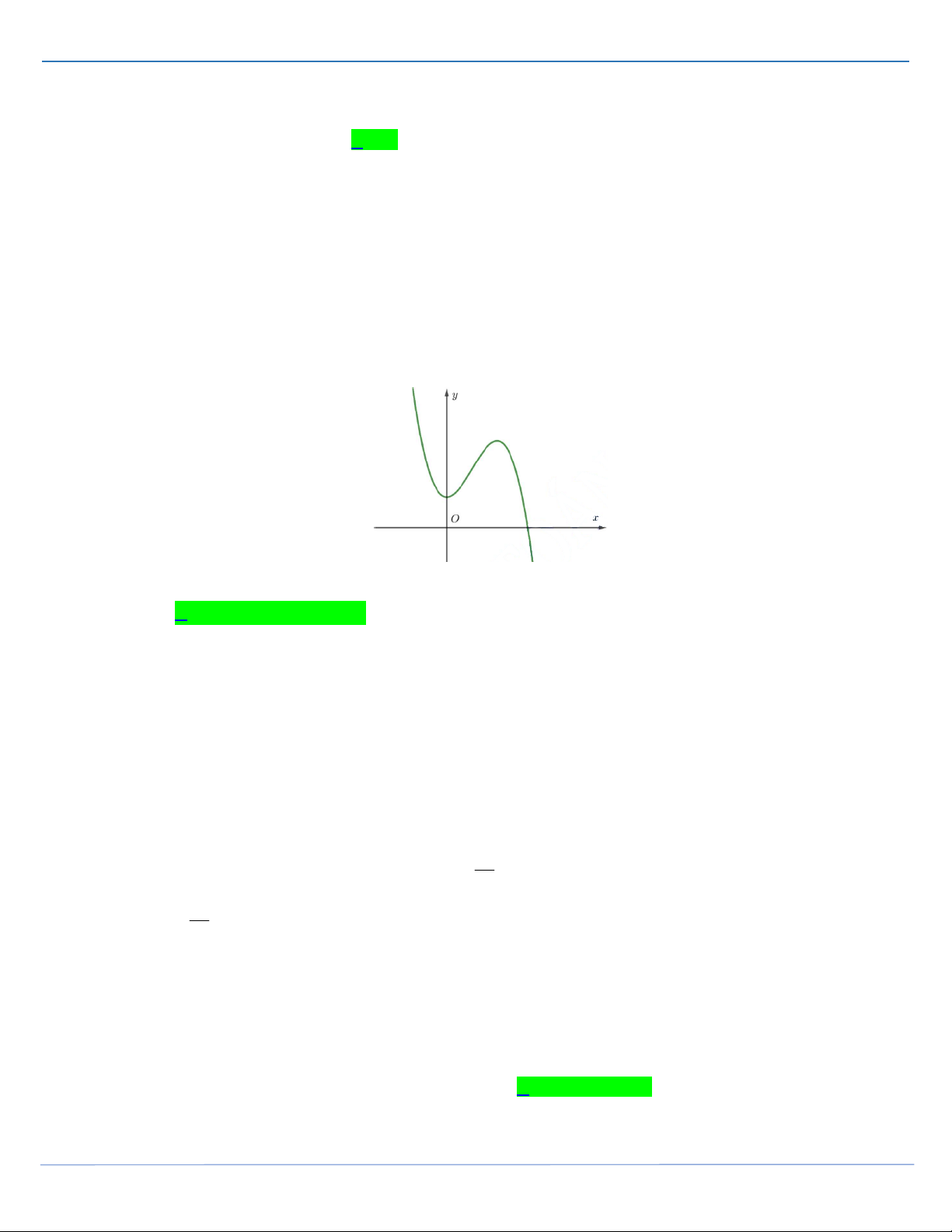
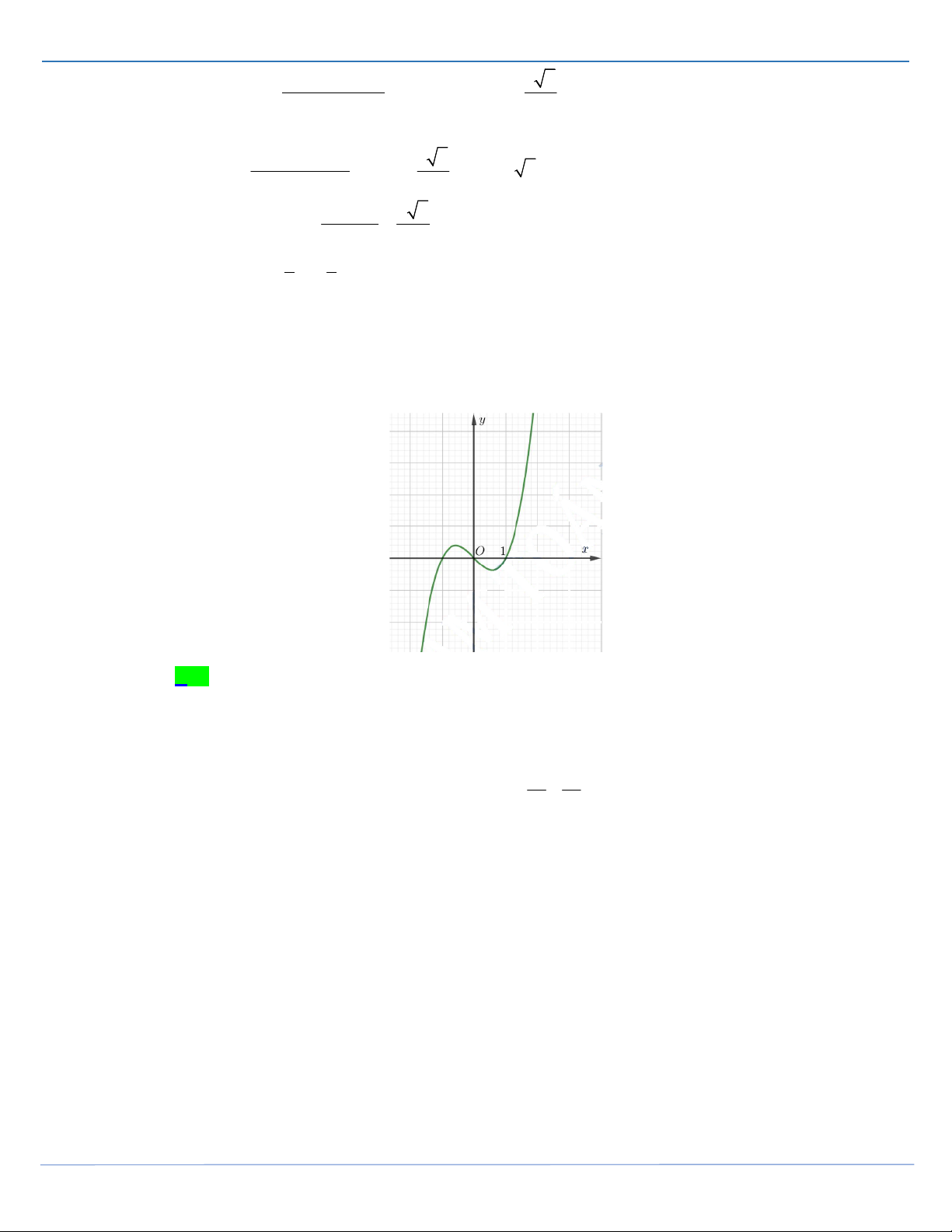
y ax bx cx d có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng?
A. a 0,b 0, c 0, d 0 .
B. a 0,b 0,c 0, d 0
C. a 0,b 0,c 0, d 0 .
D. a 0,b 0, c 0, d 0 .
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ABC . Gọi P là mặt phawgrn
qua B và vuông góc với đường thẳng SC . Thiết diện do mp P cắt hình chóp S.ABC là: A. Tam giác đều. B. Tam giác cân. C. Tam giác vuông D. Hình thang vuông.
Câu 15: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt? A. Ba mặt. B. Hai mặt. C. Năm mặt. D. Bốn mặt.
Câu 16: Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là 3V V 2V 3V A. r . B. r . C. r . D. r . 2 h h h h
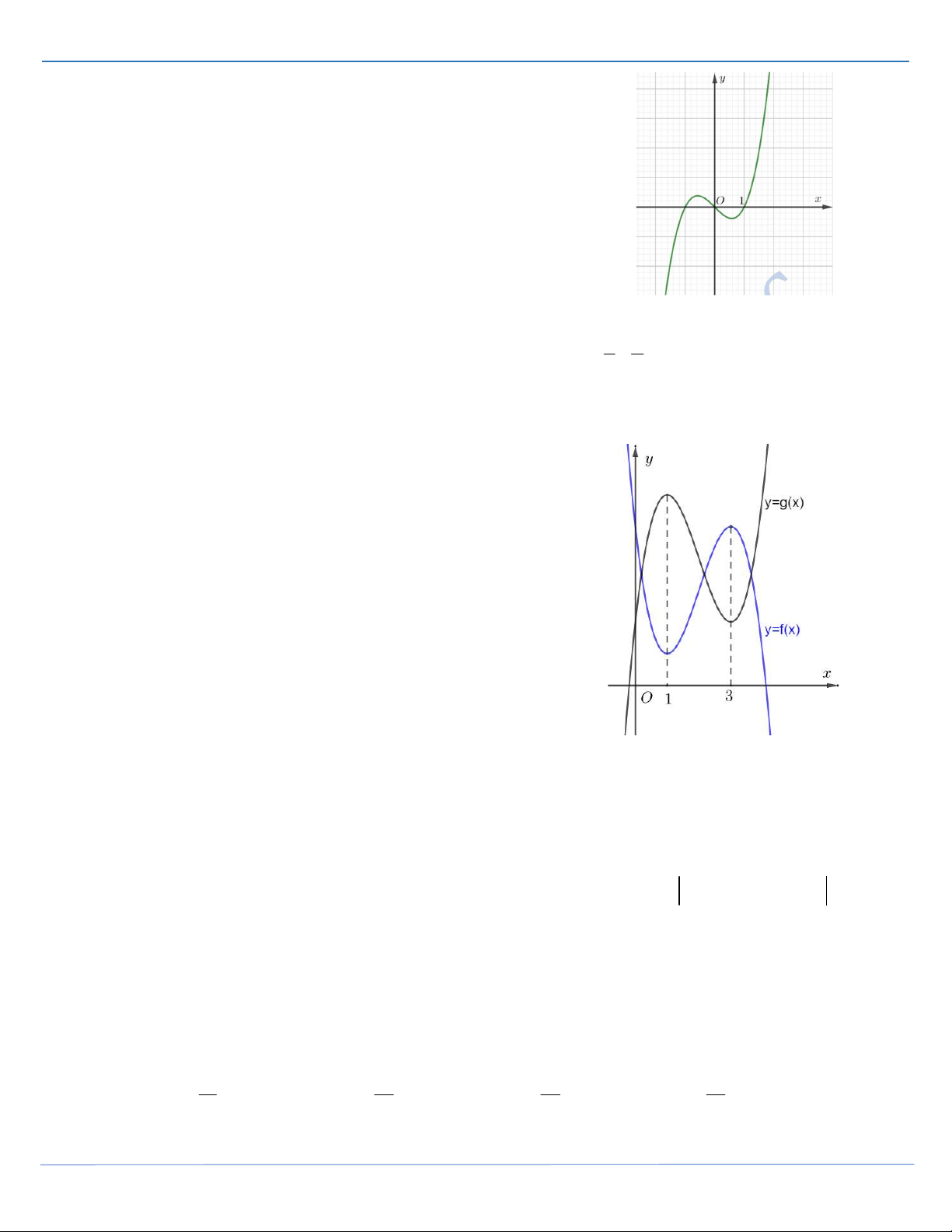
Câu 17: Đường cong trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số sau? A. 4 2 y x 2x 3 . B. 4 2 y x 2x 4 . C. 4 2 y x 2x 3 . D. 4 2 y x 2x 3.
Câu 18: Giả sử khai triển 1 2xn 2 a a x a x ... n
a x , biết rằng a a a 71. Tính hệ số a 0 1 2 n 0 1 2 5 .A. 672 . B. 627 . C. 672 . D. 627 .
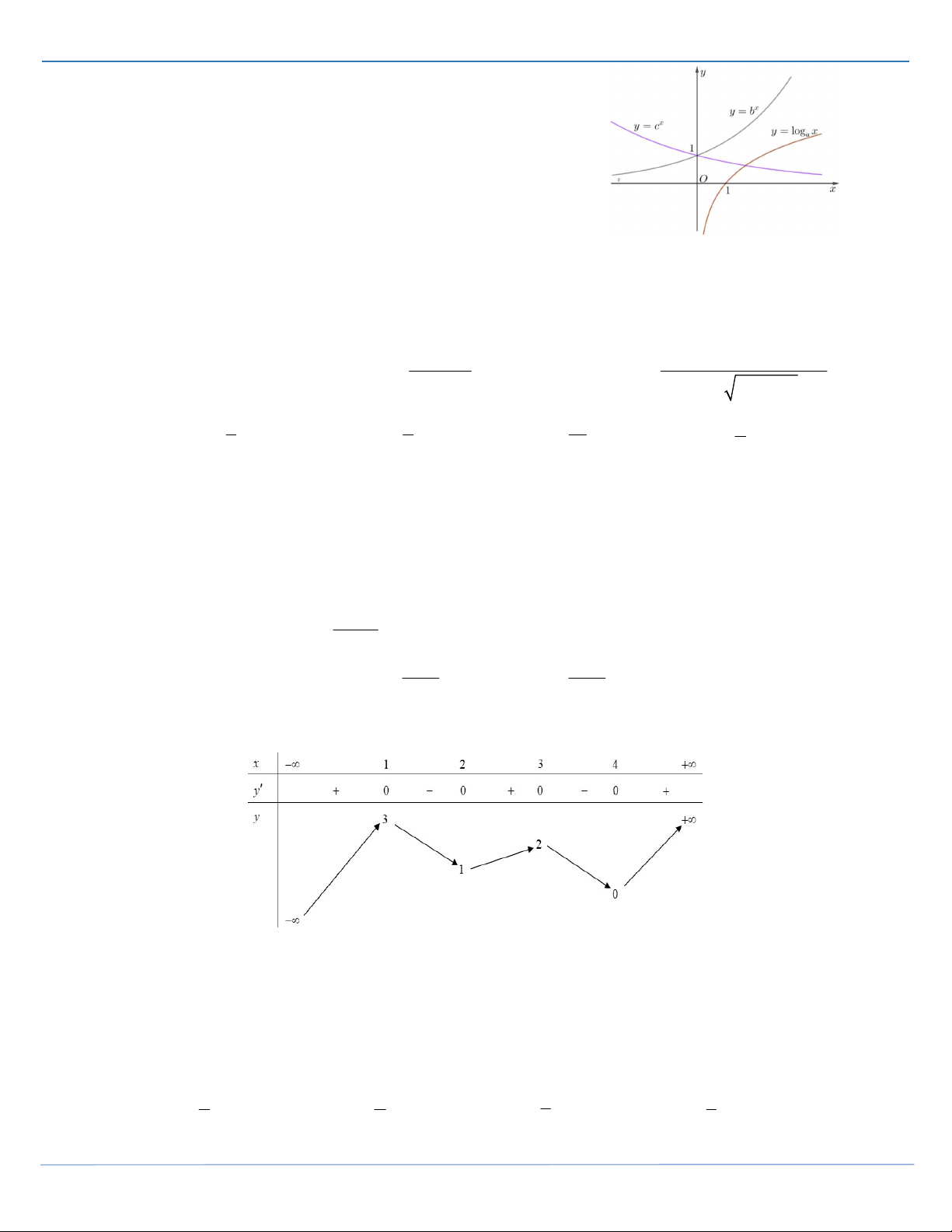
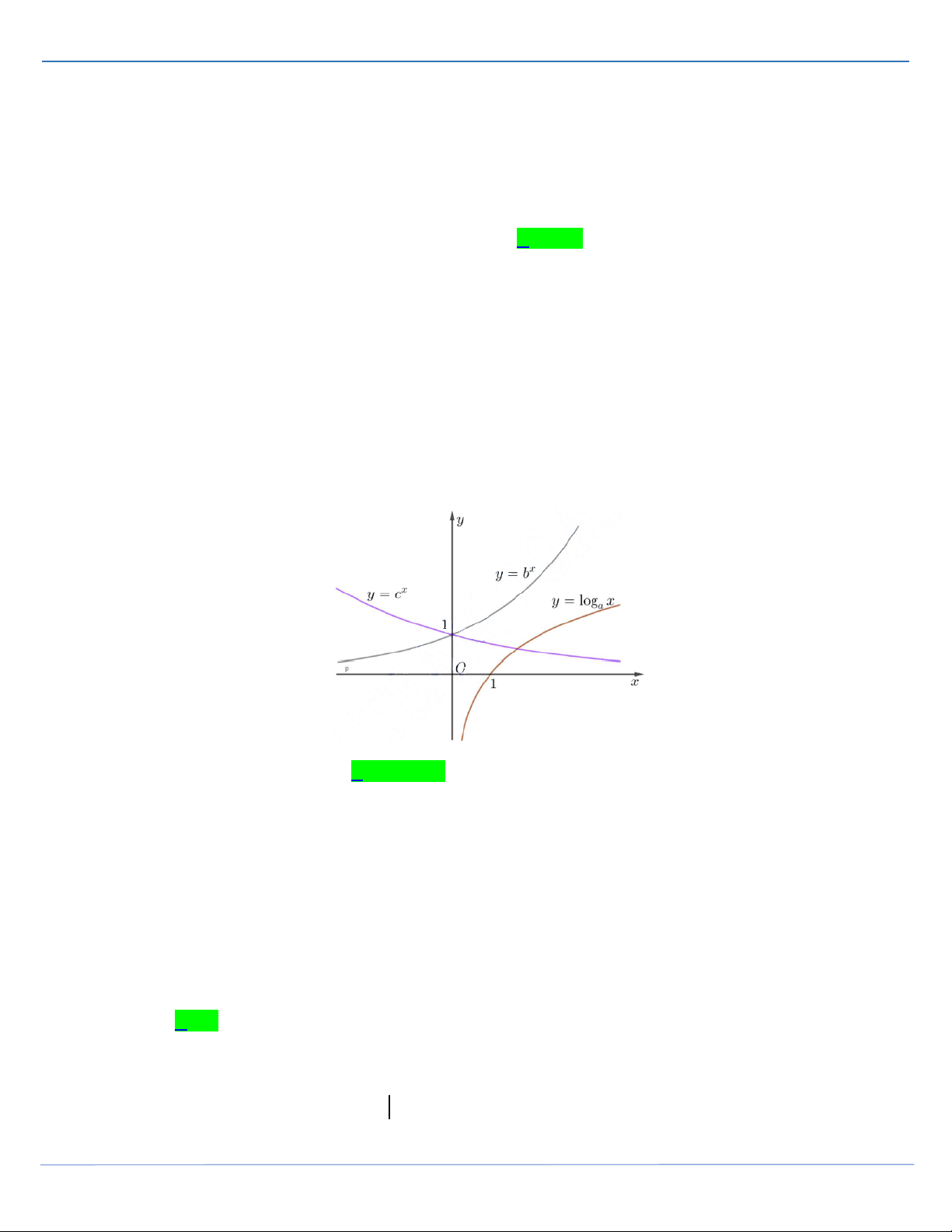
Câu 19: Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y log x, x y b , x y c được cho trong a
hình vẽ bên. Mệnh đề nào dưới đây đúng?
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 2
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 A. b c a . B. c b a . C. a b c . D. a c b .
Câu 20: Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;4, 4 f 1 12 và f
xdx 17 . Khi đó f 4 bằng 1 A. 29 . B. 9 . C. 5. D. 19. P x 2 P x 2
Câu 21: Cho đa thức P x thõa mãn lim
2.Tính giới hạn L lim . x3 x 3 x3 2
x 9 Px 2 1 1 1 1 2 A. L . B. L . C. L . D. L . 9 6 12 9
Câu 22: Với mọi số thực m, n, p thõa mãn p log 2 m log 8 n log 4 . Mệnh đề nào sau đây đúng? A. 2p 8m 4n B. log 8m 4n p . C. p 3n 2m . D. p 3m 2n .
Câu 23: Một nghuyên hàm của hàm số 2 f (x) 3x sin x là A. 3 x cos x 2021 B. 3 3x cos x 2021. C. 3 x sin x 2021. D. 3 x cos x 2021 . 2021x
Câu 24: Cho hàm số f (x) ln Tính tổng S f '
1 f '2 ... f '2022 x 1 2021 2022 A. S ln 2021 B. S . C. S . D. S 2022 . 2022 2023
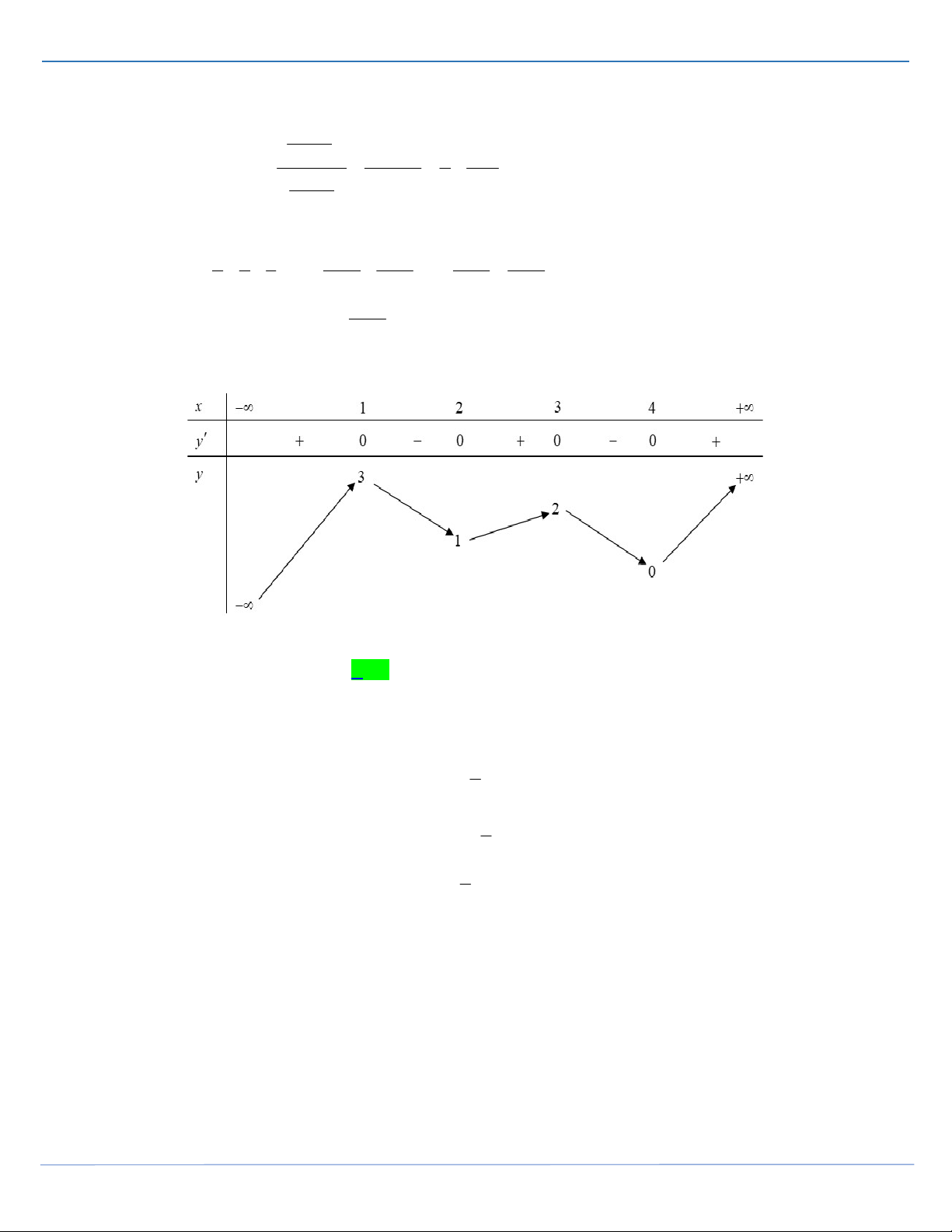
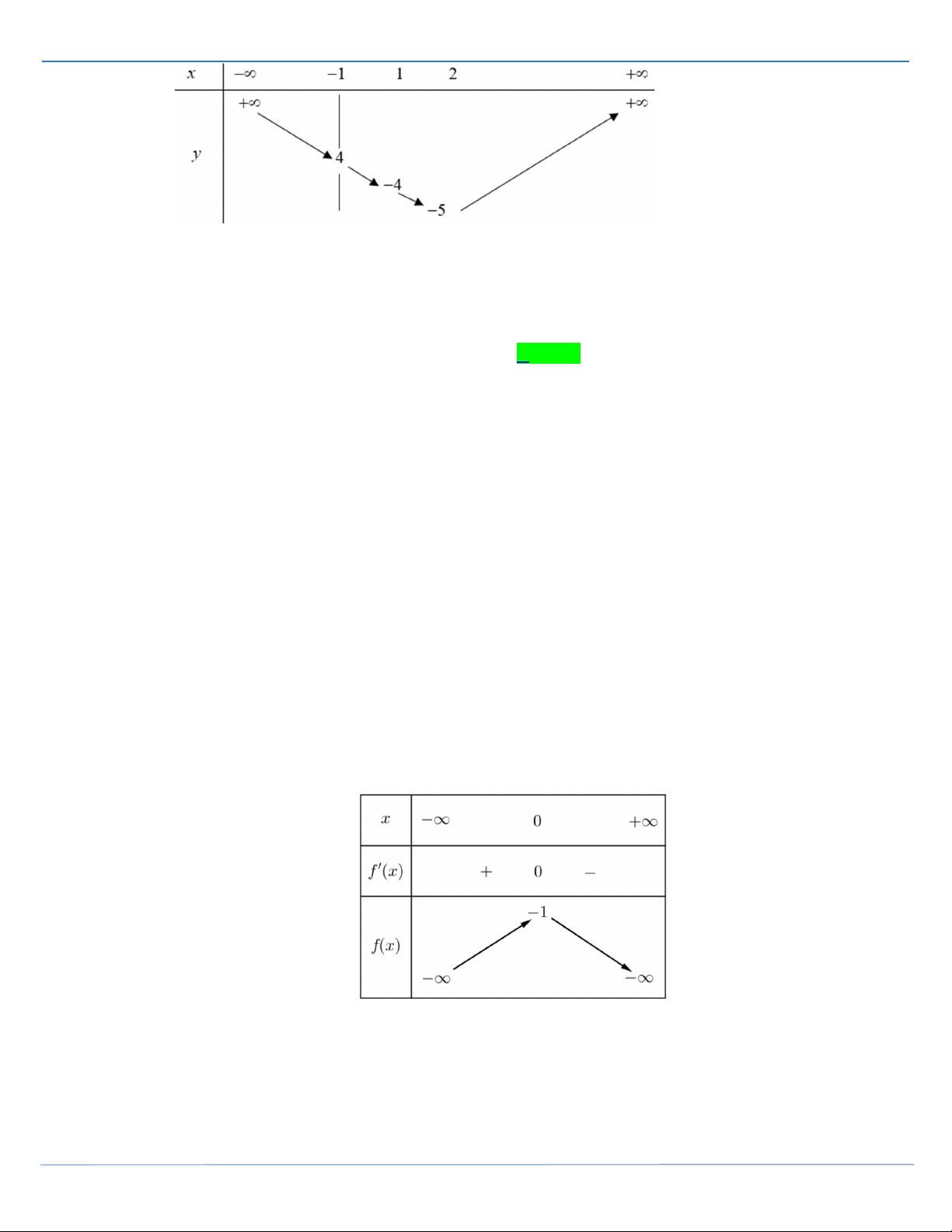
Câu 25: Cho hàm số y f x liên tục trên và có bảng biến thiên như sau
Số nghiệm của phương trình 2. f x 20 21 3 là A. 4 . B. 5 . C. 2 . D. 3 .
Câu 26: Cho hình hộp chữ nhật ABC . D A B C D
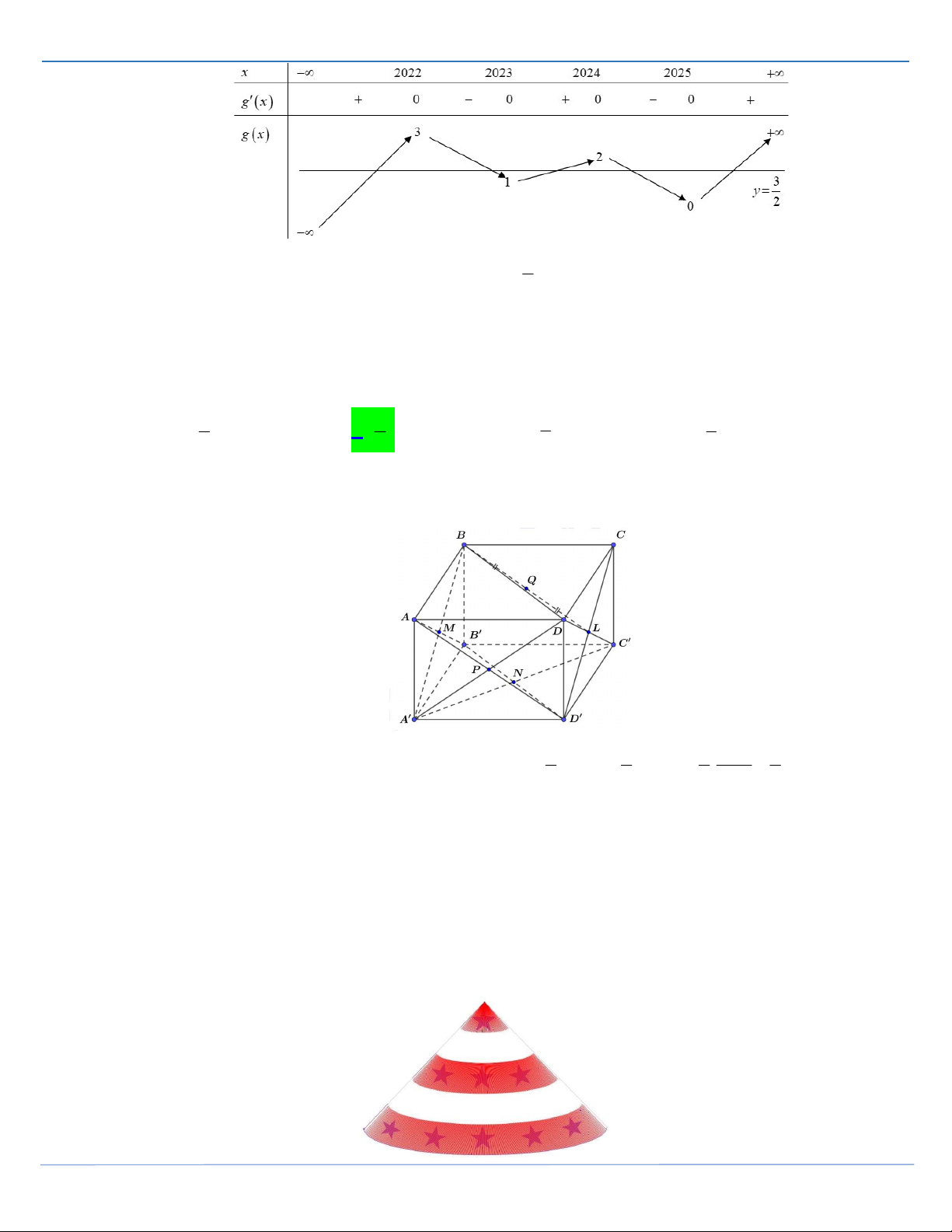
có AB 1, AD 2 và AA 3. Gọi M , N, P, L lần
lượt là tâm của các hình chữ nhật ABB A , A B C D , ADD A ,CDD C
và gọi Q là trung điểm
của đoạn BL . Thể tích của khối tứ diện MNPQ bằng 1 1 1 3 A. . B. . C. . D. . 2 4 3 8
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 3
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Câu 27: Để chuẩn bị cổ vũ cho đội tuyển Việt Nam tham dự
giải AFF Suzuki Cup 2020, một hội cổ động viên dự
định sơn và trang trí cho 1000 chiếc nón lá như sau:
Độ dài đường sinh của chiếc nón lá là 40cm , theo
độ dài đường sinh kể từ đỉnh nón cứ 8cm thì sơn
màu đỏ, màu vàng xen kẽ nhau, sau đó dán 20 ngôi
sao màu vàng cho mỗi chiếc nón (như hình minh
họa bên). Biết rằng đường kính của đường tròn đáy
nón là 40cm , mỗi ngôi sao màu vàng và công dán
giá 400 đồng, tiền sơn và công sơn màu vàng giá
30.000 đồng/m2 và tiền sơn và công sơn màu đỏ giá
40.000 đồng/m2. Hỏi giá thành để sơn và trang trí cho 1000 chiếc nón lá như trên là bao nhiêu? A. 17.047.787 đồng.
B. 16.545.123 đồng. C. 16.545.132 đồng. D. 17.047.778 đồng.
Câu 28: Có bao nhiêu giá trị nguyên của tham số m trong khoảng 2 021;202 1 để phương trình 2 x 1 m x 2 6.2 7
48 .2 2m 16m 0 có hai nghiệm x , x thỏa mãn x .x 15? 1 2 1 2 A. 1997 . B. 1996 . C. 2021. D. 2020 .
Câu 29: Cho hình lăng trụ ABC.A' B 'C ' có 0
BAC 60 , AC 120, AB 40 và khoảng cách giữa hai đáy
là 45 . Biết hình chiếu của A' lên mặt đáy ABC là điểm H thuộc cạnh BC . Hai mặt phẳng
ABB ' A', ACC ' A' cùng tạo với mặt đáy góc bằng nhau. Khoảng cách giữa hai đường thẳng
AB ' và A'C gần nhất với số nào sau đây? A. 10 . B. 7 . C. 32 . D. 21 . x e 1 ; x 0
Câu 30: Cho hàm số f x
. Biết rằng hàm số f x liên tục trên và tích 2
2x x 3 2 ; x 0 e f ln x phân dx ae b 3 c
với a,b,c . Giá trị a b 9c bằng x 1 e A. 69 . B. 33 . C. 13 . D. 25 . Câu 31: Cho hàm số 3 2
y x mx 3x 1 C và điểm M 1; 2
. Biết có hai giá trị m là m và m để 1 2
đường thẳng : y x 1 cắt đồ thị C tại ba điểm phân biệt A0; 1 , B và C sao cho tam
giác MBC có diện tích bằng 4 2 . Hỏi tổng 2 2
m m thuộc khoảng nào trong các khoảng sau 1 2 đây? A. 3;5 . B. 15;17 . C. 16;18 . D. 31;33 .
Câu 32: Cho hình lăng trụ ABC .
D A' B 'C ' D ' có đáy ABCD là hình chữ nhật với
AB 6, AD 3, A'C 3 và mặt phẳng ACC ' A' vuông góc với đáy. Biết hai mặt phẳng 3
ACC ' A' và ABB' A' tạo với nhau góc với tan . Thể tích V của khối tứ diện 4 BDA'C ' là 8 16 A. V 16. B. V 8 . C. V . D. V . 3 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 4
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
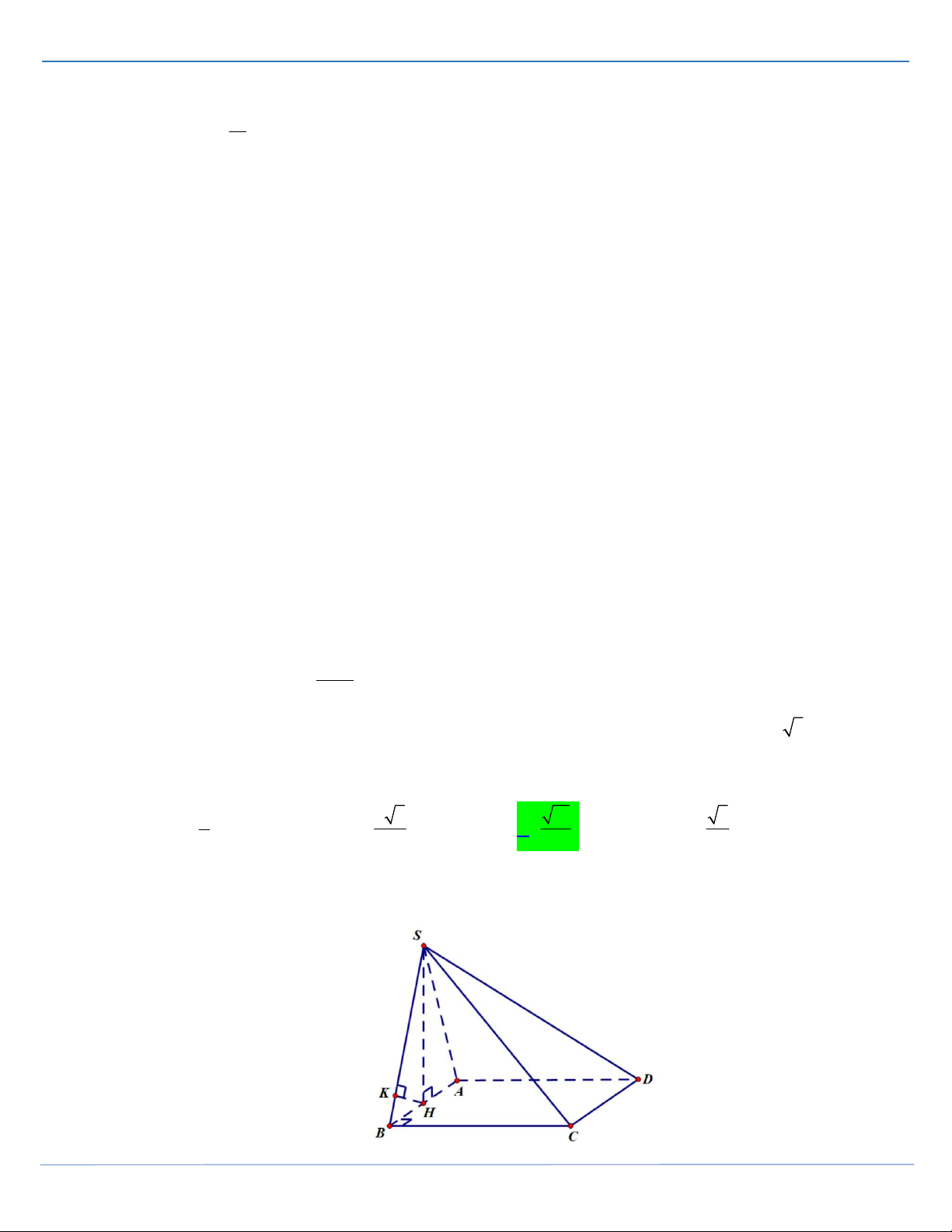
Câu 33: Cho hàm số y f x có đạo hàm 3 2
f x ax bx cx d (
a,b, c, d là các số thực). Hàm số y f x có đồ thị như hình vẽ bên và f
1 0 . Số điểm cực tiểu của hàm số
g x f 1 2x f 2 x là A. 3. B. 5. C. 2. D. 4. 2 2
Câu 34: Xét các số thực dương x , y thỏa mãn 2 2 2 4(x y 4) log
(xy 4) . Khi x 4y đạt 2 x y
giá trị nhỏ nhất, giá trị của x 2 y bằng A. 0 . B. 9 . C. 9 . D. 6 .
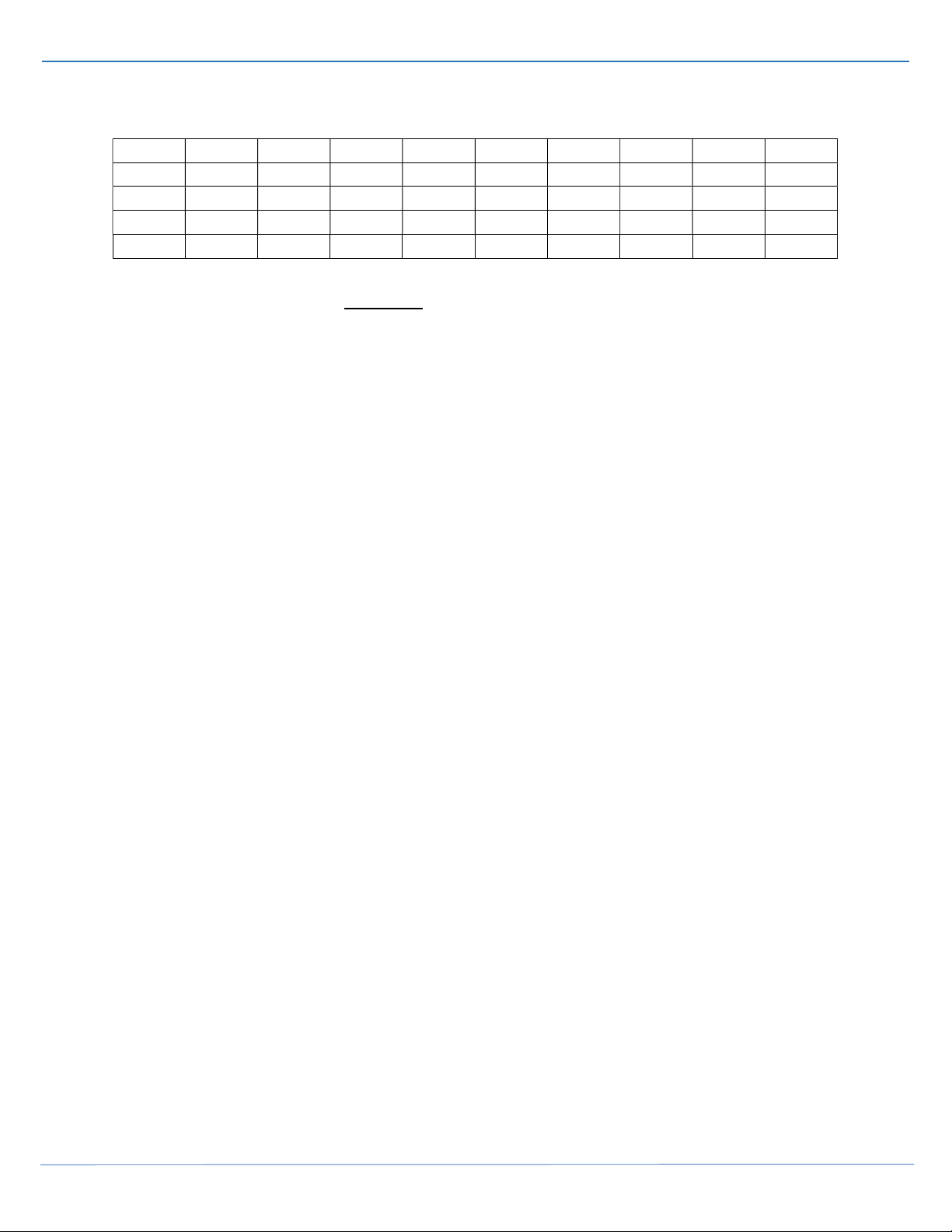
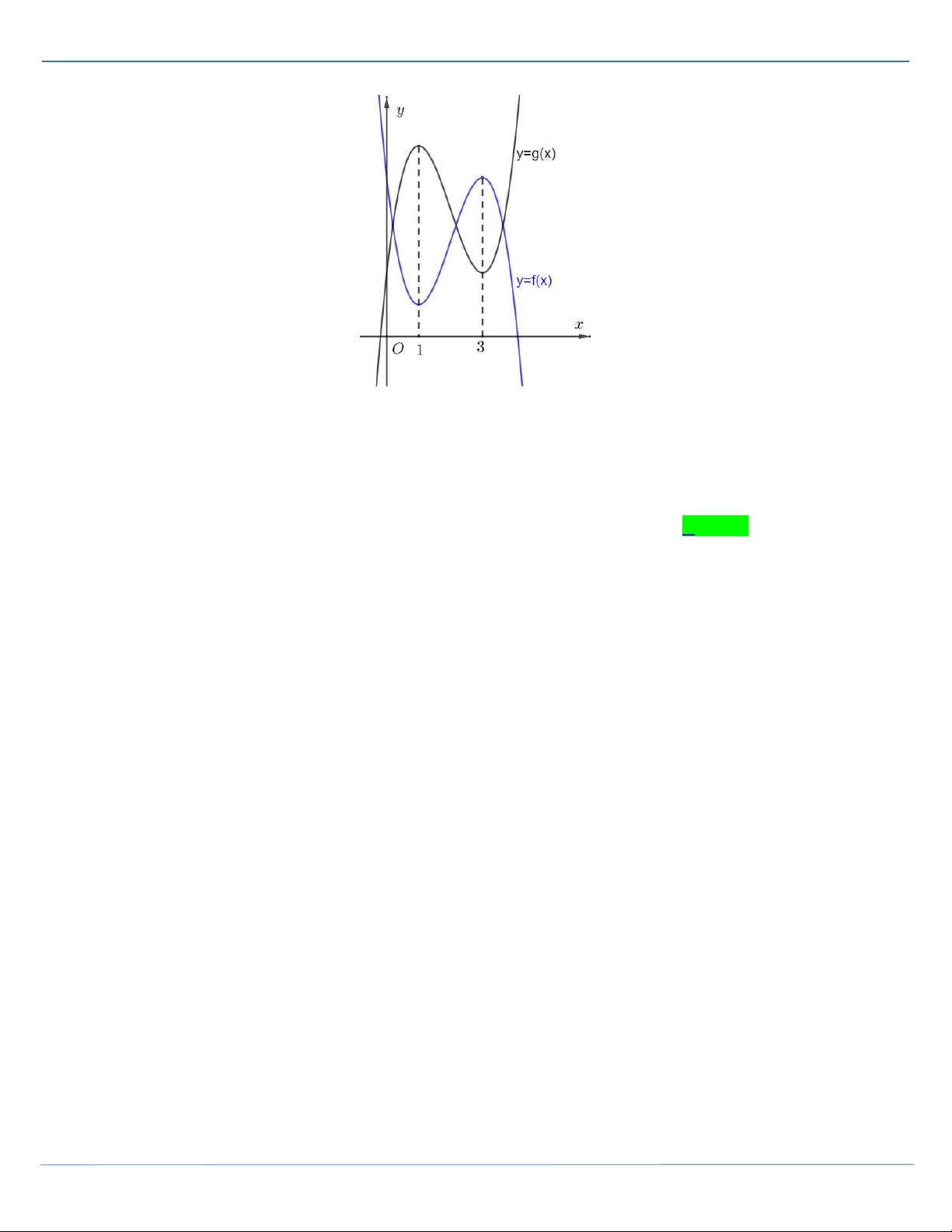
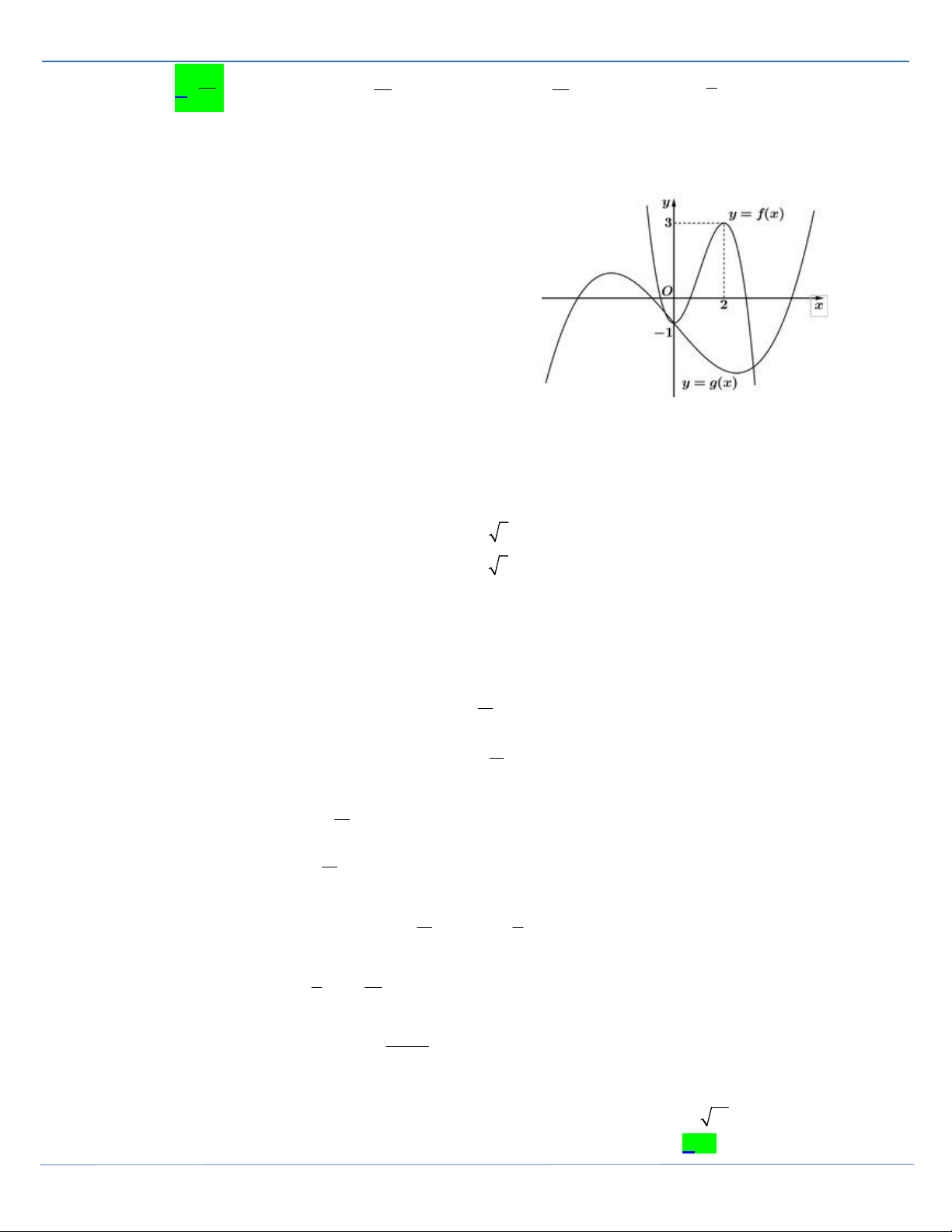
Câu 35: Cho hai hàm số bậc ba y f x, y g x có đồ thị như hình vẽ.
Biết rằng x 1, x 3 đều là các điểm cực trị của hai hàm số
y f x, y g x đồng thời 3 f
1 g 3 1, 2 f 3 g 1 4 và
f 2x 7 g 2x 3 1. Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số S x 2 f x g x 2 .
g x 27 f x 4g x 2 trên
đoạn 1;3 . Tính M m. A. 2 25. B. 1 84. C. 1 54. D. 1 70 . Câu 36: Cho hàm số 3 2 y x x 2 m 2 8
11 x 2m 2 ( m là tham số). Có bao nhiêu giá trị nguyên
của tham số m để đồ thị hàm số có hai điểm cực trị ở về hai phía của trục Ox ? A. 8 . B. 5 . C. 7 . D. 6 .
Câu 37: Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2 y 3x 4x 12x m
nghịch biến trên khoảng ; 1 ? A. 3 . B. 4 . C. 6 . D. 5 .
Câu 38: Cho ba mặt cầu S , S , S có bán kính lần lượt là R , R , R đôi một tiếp xúc với nhau và 1 2 3 1 2 3
cùng tiếp xúc với mặt phẳng P . Các tiếp điểm của ba mặt cầu với mặt phẳng P lập thành
một tam giác có độ dài ba cạnh lần lượt là 2,3, 4 . Tính tổng R R R ? 1 2 3 61 59 67 53 A. . B. . C. . D. . 12 12 12 12
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 5
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Câu 39: Cho hai hàm số bậc ba y f x và y g x f mx
n , (trong đó m,n ) có đồ thị như
hình vẽ bên. Biết rằng điểm cực tiểu của hàm số y g x lớn hơn điểm cực đại của hàm số
y g x là 5 đơn vị và g0 1
. Khi đó giá trị biểu thức P 3m 2n là 16 19 11 4 A. . B. . C. . D. . 5 2 2 5 2x 1 Câu 40: Cho hàm số y
C và điểm M C . Tiếp tuyến của C tại M cắt đường tiệm cận x 1
ngang của đồ thị tại điểm A . Hỏi có bao nhiêu điểm M thuộc đồ thị C có tọa độ là các số
nguyên để điểm A cách gốc tọa độ một khoảng nhỏ hơn 2 10 ? A. 4 B. 6 C. 5 D. 3.
Câu 41: Cho K là tập hợp các số tự nhiên có bốn chữ số, chọn ngẫu nhiên một số từ K . Tính xác suất
để số được chọn có tổng các chữ số là bội của 4. 2243 2226 2250 2249 A. . B. . C. . D. . 9000 9000 9000 9000
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD a 3 . Mặt bên SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng
SD và mặt phẳng SBC bằng 1 2 5 13 3 A. . B. . C. . D. . 4 5 4 4 x 1 Câu 43: Cho hàm số y
( m là tham số). Tập hợp các giá trị của tham số m để 2 2x 2x m x 1
đồ thị hàm số có bốn đường tiệm cận là
A. m 5;4 \ 4 . B. m 5 ;4 \ 4 . C. m 5 ;4.
D. m 5;4 \ 4 .
Câu 44: Có bao nhiêu giá trị nguyên của m thuộc đoạn 0;202 1 để phương trình 3 3 3 ln 3 ln m x x x m m e x m
e có nghiệm lớn hơn 6? A. 2021. B. 1010 . C. 1624 . D. 2020 .
Câu 45: Cho hàm số y f x có đạo hàm liên tục trên và thỏa mãn điều kiện 1 a
f x f x 2 5 7 1
3 x 2x,x . Biết rằng tích phân I . x f xdx (với a,b là 0 b a
các số nguyên dương và là phân số tối giản). Tính T 3a b . b A. T 48 . B. T 16 . C. T 0 . D. T 1. Câu 46: Cho phương trình 2020 2020 x x 2022 2022 sin cos 2 sin x cos
x. Tổng các nghiệm của phương
trình trong khoảng 0; 20 21 bằng 2 12 87 2 12 87 A. . B. 2 643 . C. . D. 2 644 . 2 4
Câu 47: Một tỉnh A đưa ra nghị quyết về giảm biên chế cán bộ công chức, viên chức hưởng lương từ
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 6
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
ngân sách nhà nước trong giai đoạn 2015 2021( 6 năm) là 9,9% so với số lượng hiện có năm
2015 theo phương thức “ra 2 vào 1”(tức là khi giảm đối tượng hưởng lương từ ngân sách nhà
nước 2 người thì được tuyển mới 1 người). Giả sử tỷ lệ giảm và tuyển dụng mỗi năm so với
năm trước đó là như nhau. Tính tỷ lệ tuyển dụng mới hàng năm(làm tròn đến 0,01% ). A. 1, 72% . B. 2, 06% . C. 1,13% . D. 1,85% .
Câu 48: Có bao nhiêu bộ ;
x yvới x, y là các số nguyên và 1 x, y 2021 đồng thởi thỏa mãn điều 2y 2x 1
kiện xy 2x 4y 8log 2x 3y xy 6 log ? 3 2 y 2 x 3 A. 2018.2021. B. 2 . C. 4036 . D. 2018 .
Câu 49: Cho khối trụ T có hai đáy là hai hình tròn O và O . Xét hình chữ nhật ABCD có hai điểm ,
A B cùng thuộc đường tròn O và hai điểm C, D cùng thuộc đường tròn O sao cho
AB a 3, BC 2a đồng thời mặt phẳng ABCD tạo với mặt đáy của hình trụ một góc 60 .
Thể tích khối trụ T bằng 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. 3 2 a 3 . 3 9
Câu 50: Cho hình chóp S.ABC , có đáy ta giác ABC vuông tại ,
A AB a 2 , AC a 5 . Hình chiếu
của điểm S trên mặt phẳng ABC trùng với trung điểm của đoạn thẳng BC . Biết góc giữa
mặt phẳng SAB và mặt phẳng SAC bằng 60 . Thể tích của khối chóp S.ABC là 3 a 30 3 5a 10 3 5a 6 3 a 210 A. . B. . C. . D. . 12 12 12 24
_______________ HẾT _______________
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 7
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 BẢNG ĐÁP ÁN 1.D 2.C 3.D 4.A 5.D 6.B 7.C 8.C 9.B 10.B 11.D 12.B 13.C 14.C 15.A 16.B 17.C 18.C 19.B 20.A 21.A 22.D 23.A 24.C 25.B 26.B 27.A 28.B 29.D 30.B 31.D 32.C 33.A 34.A 35.D 36.B 37.D 38.A 39.A 40.D 41.D 42.C 43.A 44.C 45.D 46.A 47.A 48.C 49.B 50.A
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 7
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 LỜI GIẢI CHI TIẾT x
Câu 1: [Mức độ 2] Cho F x là một nguyên hàm của hàm số f x thỏa mãn F 2 0 . 2 8 x
Tính số nghiệm phương trình F x x . A. 2 . B. 0 . C. 3 . D. 1. Lời giải FB tác giả: Nguyễn Loan 1 d 2 8 x 1 1 1 x x F dx 2 8 x d 2 8 x 2 2 8 x 2 C . 2 8 x 2 2 8 x 2 Vậy F x 2
8 x C F 2 0 c 2 c 2 . Phương trình: 2 2
2 8 x x 8 x 2 x 2 2 x 2 2 2 x 2 2 2 x 2 x 1 3 . 2 2
x 4x 4 8 x 2 x 2x 2 x 1 3
Vậy phương trình F x x có một nghiệm
Câu 2: [Mức độ 1] tập xác định của hàm số y log 2 x 7x 10 là 2 A. ; 25; . B. 2;5.
C. ;2 5; . D. 2;5 . Lời giải FB tác giả: Nguyễn Loan x 5 Đk: 2 x 7x 10 0 . x 2
Vậy TXĐ của hàm số D ; 25; .
Câu 3: [Mức độ 3] Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2 021;202 1 để hàm 1 số y ln 2
x 4 mx 2 nghịch biến trên khoảng ; ? 2 A. 2022. B. 2019. C. 2021. D. 2020. Lời giải
FB tác giả: Minh Nguyễn Quang 1 x Hàm số y ln 2
x 4 mx 2 có đạo hàm y m . 2 2 x 4 x
Để hàm số đã cho nghịch biến trên khoảng ; thì y m 0 , x ; . 2 x 4 x x Suy ra m , x ; m Max . 2 x 4 2 ; x 4
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 8
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 x x 1 x 1 Mà 2 x 4 4 x , x ; , x ; Max . 2 2 x 4 x 4 4 2 ; x 4 4 1 1
Suy ra m . Thử lại ta có m thỏa mãn. 4 4
Vậy có 2020 giá trị nguyên của tham số m thuộc khoảng 2 021;202 1 thỏa mãn.
Câu 4: [Mức độ 2] Cho hàm số f x có đạo hàm f x x 2 x 4 1 3 x 1 , x . Số điểm
cực trị của hàm số y f x là A. 3. B. 2. C. 1. D. 4. Lời giải
FB tác giả: Minh Nguyễn Quang
Ta có f x x 2 x x x 2 1 1 3 3 x 1 . x Suy ra f x 1 0
nên ta có bảng xét dấu như sau x 3
Vậy hàm số y f x có 3 điểm cực trị.
Câu 5: [Mức độ 2] Cho khối lăng trụ đứng ABC.AB C
có đáy ABC là tam giác cân với AB AC a , 0
BAC 120 . Mặt phẳng AB C
tạo với đáy một góc 0 60 . Tính thể tích V
của khối lăng trụ đã cho. 3 a 3 3a 3 9a 3 3a A. V . B. V . C. V . D. V . 8 4 8 8 Lời giải FB tác giả: Hanh Nguyen Gọi H là trung điểm B C , ta có B C AH .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 9
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 Vì AA AB C ' nên AA B C . Từ đó B C
AAH nên B C
AH . Vậy góc giữa hai mặt phẳng AB C
và ABC bằng AHA , nên 0 AHA 60 . a Vì tam giác AB C cân tại A , 0 B A C 120 0 HAC 60 0 AH A'C '.cos60 . 2 a 3 Ta có 0 AA' A H .tan 60 . 2 3 1 a 3 3a Vậy 0 V S .AA . a . a sin120 . . A B C ' 2 2 8
Câu 6: [Mức độ 2] Cho hàm số y f x , biết f 3 0 và 2 . x f x
x e , x . Tính tích phân 2 1 I xf xd .x 0 e 3 e 1 e 1 e 2 A. I . B. I . C. I . D. I . 4 4 2 4 Lời giải FB tác giả: Hanh Nguyen x 1 x 1 Ta có 2 2 . 2 2 x f x dx x e dx e d x e C . 2 2 3 1 Mà 0 2 x f f x e 1 . 2 2 Do đó 2 1 1 1 1 1 1 1 1 x 2 I xf x 1 2 e x e x 1 2 x 1 2 dx x e 1 x dx xe dx xdx e d 1 2 x xdx . 2 2 4 4 2 4 0 0 0 0 0 0 0 0
Câu 7: [Mức độ 2] Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB 2a . Tam
giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC . 3 a 3 3 4a 3 3 2a 3 3 a 3 A. . B. . C. . D. . 3 3 3 12 Lời giải
FB tác giả: Nguyễn Văn Phu
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 10
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 1 1 Ta có AC AB a , 2 S A . B AC .2 . a 2a 2 ABC a
. Gọi H là trung điểm của AB , khi 2 2 đó do S
AB đều nên SH AB , mà SAB ABC AB SH ABC . 3 Ta có S
AB đều cạnh 2a SH 2 . a a 3 . 2 2 1 1 2a 3 Vậy 2 S V . SH.S .a 3.2 ABC a . 3 A BC 3 3
Câu 8: [Mức độ 2] Cho mặt cầu 1
S có bán kính là a , mặt cầu S2 có bán kính là 2a . Tỷ số diện tích của mặt cầu 1
S và mặt cầu S2 bằng 1 1 A. . B. 4 . C. . D. 2 . 2 4 Lời giải
FB tác giả: Nguyễn Văn Phu
- Diện tích mặt cầu 1 S là 2 2 1 S 4 1 R 4 a . S 2 S 2 4 2 R 4 2a2 2 2 16 a - Diện tích mặt cầu là . 2 S 4 a 1
- Tỷ số diện tích của mặt cầu 1 1
S và mặt cầu S2 là: . 2 S2 16 a 4
Câu 9: [ Mức độ 1] Cho hình đa diện đều loại 4;
3 có cạnh bằng a . Gọi S là tổng diện tích tất cả
các mặt của hình đa diện đó. Mệnh đề nào sau đây là đúng? A. 2 S 4a . B. 2 S 6a . C. 2 S 2 3a . D. 2 S 3a . Lời giải FB tác giả: Nguyễn Trinh 4;
3 là hình lập phương cạnh a
Vậy tổng diện tích 6 mặt của hình là 2 S 6a .
Câu 10: [ Mức độ 1] Tập giá trị của hàm số y 2sin 2x 3 là A. 2; 2 . B. 1;5 C. 2;5. D. 1; 2 . Lời giải FB tác giả: Nguyễn Trinh Ta có sin 2x 1; 1 2sin 2x 31;5.
Câu 11: [Mức độ 1] Số cách xếp 5 người ngồi vào một hàng ghế dài là A. 130 . B. 100 . C. 125 . D. 120 . Lời giải FB tác giả: Đinh Len
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 11
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Số cách xếp 5 người ngồi vào một hàng ghế dài là 5!120 (cách).
Câu 12: [Mức độ 2] Cho cấp số cộng u thỏa mãn u 3 và u 18 . Số hạng u bằng n 1 6 10 A. 27 . B. 30 . C. 2 4. D. 21. Lời giải FB tác giả: Đinh Len u 3 u 3 u 3 Ta có 1 1 1 . u 18 u 5d 18 d 3 6 1
Vậy u u 9d 39.3 30. 10 1
Câu 13: [Mức độ 2] Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a 0,b 0, c 0, d 0 .
B. a 0,b 0,c 0, d 0
C. a 0,b 0,c 0, d 0 .
D. a 0,b 0, c 0, d 0 . Lời giải
FB tác giả: Nguyễn Công Thiện
Ta thấy lim y nên a 0 . x
Đồ thị cắt Oy tại điểm nằm phía trên Ox nên d 0 . Ta có: 2
y 3ax 2bx c , y 0 có 1 nghiệm bằng 0 nên c 0 . x 0 Khi đó: 2
y 0 3ax 2bx 0 2b
. Ta thấy điểm cực đại nằm bên phải Oy nên x 3a 2b 0 b 0 . 3a
Vậy a 0,b 0, c 0, d 0 .
Câu 14: [Mức độ 1] Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ABC . Gọi P là
mặt phawgrn qua B và vuông góc với đường thẳng SC . Thiết diện do mp P cắt hình chóp S.ABC là: A. Tam giác đều. B. Tam giác cân. C. Tam giác vuông D. Hình thang vuông. Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 12
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
FB tác giả: Nguyễn Công Thiện BE AC
Gọi E là trung điểm của AC , ta có: BE SC . BE SA
Kẻ BF SC (F SC) , khi đó BEF chính là mặt phẳng qua B và vuông góc với SC .
Vì BE SAC nên BE EF hay thiết diện là tam giác vuông BEF .
Câu 15: [Mức độ 1] Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt? A. Ba mặt. B. Hai mặt. C. Năm mặt. D. Bốn mặt. Lời giải FB tác giả: Lê Cường
Theo tính chất của hình đa diện, mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất ba mặt.
Câu 16: [Mức độ 1] Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là 3V V 2V 3V A. r . B. r . C. r . D. r . 2 h h h h Lời giải FB tác giả: Lê Cường Vì 2 2 V V V r h r r . h h
Câu 17: [Mức độ 2] Đường cong trong hình vẽ sau là đồ thị của hàm số nào trong các hàm số sau? A. 4 2 y x 2x 3 . B. 4 2 y x 2x 4 . C. 4 2 y x 2x 3 . D. 4 2 y x 2x 3 . Lời giải FB tác giả: Thu Nghia
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 13
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
+ Đồ thị hàm số giao Oy tại điểm có tọa độ 0; 3 nên loại đáp án A và B.
+ Hàm số có 3 cực trị nên ab 0 suy ra loại D. + Vậy chọn C.
Câu 18: [Mức độ 2] Giả sử khai triển 1 2xn 2 a a x a x ... n
a x , biết rằng a a a 71. 0 1 2 n 0 1 2 Tính hệ số a . 5 A. 672 . B. 627 . C. 672 . D. 627 . Lời giải FB tác giả: Thu Nghia
Số hạng tổng quát T C 1 nk 2 k x C 2 k k k k x . k 1 n n
a a a 71 C C C n n n . n n 21 n 2 2 0 1 2 2 71 2 35 0 7 0 1 2 Vậy a C 25 5 6 72 . 5 7
Câu 19: [Mức độ 2] Cho ba số thực dương a,b, c khác 1. Đồ thị các hàm số y log x, x y b , x y c a
được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng? A. b c a . B. c b a . C. a b c . D. a c b . Lời giải FB tác giả: Mai Vĩnh Phú Dựa vào đồ thị x
y c nghịch biến 0 c 1, x
y b đồng biến 1 b c b
Và hàm số y log x đồng biến 1 a . Kẻ đường thẳng y 1 lên đồ thị ta thấy b a . a Vậy c b a .
Câu 20: [Mức độ 2] Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;4, f 1 12 và 4 f
xdx 17 . Khi đó f 4 bằng 1 A. 29 . B. 9 . C. 5. D. 19. Lời giải FB tác giả: Mai Vĩnh Phú 4 Ta có f
xdx 17 f x4 17 f 4 f 1 17 f 4 17 f 1 1712 29. 1 1
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 14
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 P x 2
Câu 21: [ Mức độ 2] Cho đa thức P x thõa mãn lim 2. x3 x 3 P x 2 Tính giới hạn L lim . x3 2
x 9 Px 2 1 1 1 1 2 A. L . B. L . C. L . D. L . 9 6 12 9 Lời giải FB tác giả: Trần Thủy P x 2 Ta có lim
2 Px 2 x 3Q x trong đó Q x là đa thức. x3 x 3
Px x 3Q x 2 P3 2 P x 2 P x 2 Khi đó L lim lim x3 2
x 9 Px 2 x3 1
x 3x 3 Px2 1 P x 2 1 1 1 lim .lim 2. x3
x 3 x3 x Px 18 9 3 2 1 1 Vậy L . 9
Câu 22: [ Mức độ 2] Với mọi số thực m, n, p thõa mãn p log 2 m log 8 n log 4 . Mệnh đề nào sau đây đúng? A. 2p 8m 4n B. log 8m 4n p . C. p 3n 2m . D. p 3m 2n . Lời giải FB tác giả: Trần Thủy
Ta có log 2 log8 log 4 log 2p log8m log 4n p m n log 2p log8m.4n p 3m2 2 2 n p 3m 2n
Câu 23: [ Mức độ 1] Một nghuyên hàm của hàm số 2 f (x) 3x sin x là A. 3 x cos x 2021 B. 3 3x cos x 2021. C. 3 x sin x 2021. D. 3 x cos x 2021 . Lời giải FB tác giả: Trần Thủy Ta có f x dx 2x x 3 ( ) 3 sin dx x cos x C
Vậy hàm số cần tìm là 3
x cos x 2021 là một nguyên hàm của hàm số 2 f (x) 3x sin x 2021x
Câu 24: [ Mức độ 2] Cho hàm số f (x) ln Tính tổng S f '
1 f '2 ... f '2022 x 1 2021 2022 A. S ln 2021 B. S . C. S . D. S 2022 . 2022 2023
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 15
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 Lời giải FB tác giả: Trần Thủy 2021x ' x 1 1 1 1 Ta có f '(x) . 2021x x x 1 x x 1 x 1 Khi đó S f '
1 f '2 ... f '2022 1 1 1 1 1 1 .... 1 2022 1 2 2 3 2022 2023 2023 2023 2022
Vậy đường thẳng là S . 2023
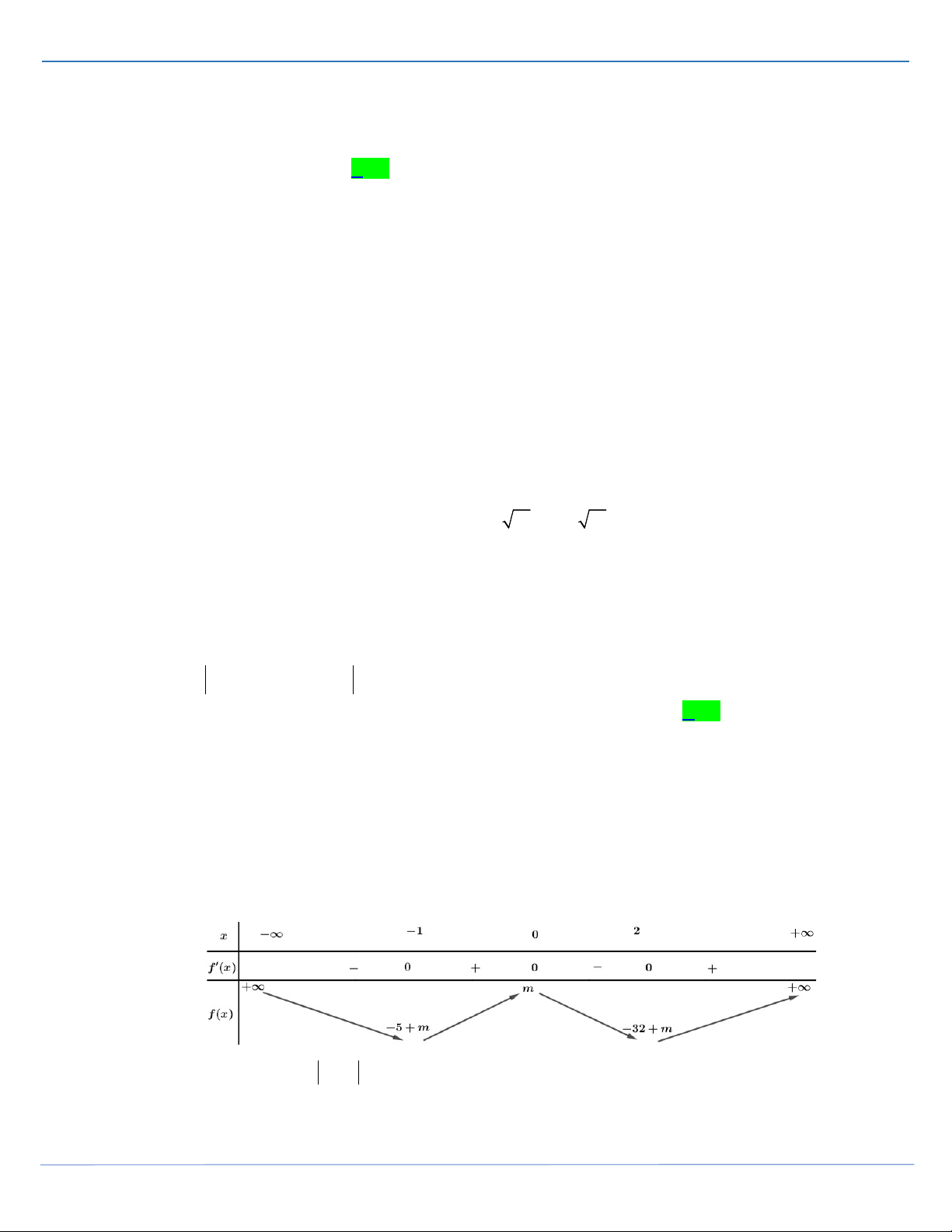
Câu 25: [Mức độ 2] Cho hàm số y f x liên tục trên và có bảng biến thiên như sau
Số nghiệm của phương trình 2. f x 20 21 3 là A. 4 . B. 5 . C. 2 . D. 3 . Lời giải Fb tác giả: Thái Huy Ta có: 2. f x 20 21 3 f x 3 2021 . 2
Số nghiệm của phương trình f x 3
2021 chính là số giao điểm của đồ thị hàm số 2 3
g x f x 202
1 và đường thẳng y . 2
Xét hàm số g x f x 202
1 có g x f x 202 1 . x 20211 x 2022 x 2021 2 x 2023
Cho gx0 f x 20 21 0 . x 20213 x 2024 x 2021 4 x 2025 Bảng biến thiên
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 16
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 3
Dựa vào bảng biến thiên ta thấy đường thẳng y cắt hàm số g x f x 202 1 tại 5 điểm. 2
Vậy phương trình đã cho có 5 nghiệm.
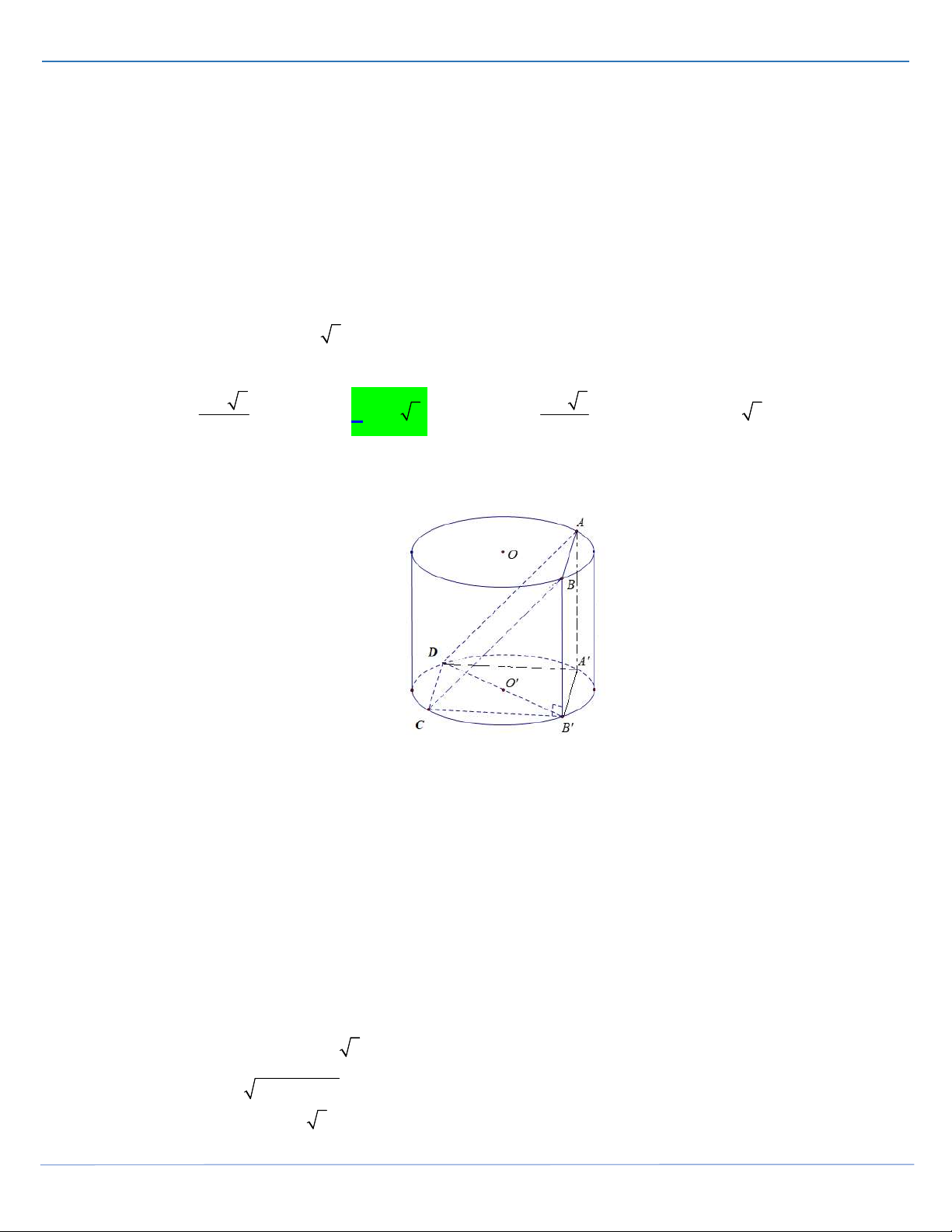
Câu 26: [ Mức độ 3] Cho hình hộp chữ nhật ABC . D A B C D
có AB 1, AD 2 và AA 3 . Gọi
M , N, P, L lần lượt là tâm của các hình chữ nhật ABB A , A B C D , ADD A ,CDD C và gọi
Q là trung điểm của đoạn BL . Thể tích của khối tứ diện MNPQ bằng 1 1 1 3 A. . B. . C. . D. . 2 4 3 8 Lời giải FB tác giả: Quang Trần 1 1 1 1.3.2 1 Ta có: BL // D M BL //MNP V V V V . . QMNP BMNP B.AD B A . 4 4 AD B 4 6 4
Câu 27: [ Mức độ 3] Để chuẩn bị cổ vũ cho đội tuyển Việt Nam tham dự giải AFF Suzuki Cup 2020,
một hội cổ động viên dự định sơn và trang trí cho 1000 chiếc nón lá như sau: Độ dài đường
sinh của chiếc nón lá là 40cm , theo độ dài đường sinh kể từ đỉnh nón cứ 8cm thì sơn màu đỏ,
màu vàng xen kẽ nhau, sau đó dán 20 ngôi sao màu vàng cho mỗi chiếc nón (như hình minh
họa bên). Biết rằng đường kính của đường tròn đáy nón là 40cm , mỗi ngôi sao màu vàng và
công dán giá 400 đồng, tiền sơn và công sơn màu vàng giá 30.000 đồng/m2 và tiền sơn và
công sơn màu đỏ giá 40.000 đồng/m2. Hỏi giá thành để sơn và trang trí cho 1000 chiếc nón lá như trên là bao nhiêu?
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 17
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 A. 17.047.787 đồng.
B. 16.545.123 đồng. C. 16.545.132 đồng. D. 17.047.778 đồng. Lời giải
FB tác giả: Nguyễn Bá Long
*) Ta tính giá thành để sơn 1 chiếc nón.
Diện tích xung quanh của 1 chiếc nón là S .0, 2.0, 4 0, 08 m2 xq
Phần màu vàng là 2 hình nón cụt, có tổng diện tích xung quanh của hai hình nón cụt màu vàng là 0,32.0,2 0,24.0,16 0,16.0,12 S . .0,08
0,04 . .0,08 0,032 m2 xqv 0, 4 0,32 0,24
Diện tích để sơn phần màu đỏ là S
0,08 0,032 0,048 m2 xqd
Giá thành để sơn và trang trí cho một nón là
400x20 30.000x0, 032 40.000x0,048 17047, 787 đồng.
Vậy để hoàn thiện 1000 chiếc nón cần 17.047.787 đồng.
Câu 28: [ Mức độ 3] Có bao nhiêu giá trị nguyên của tham số m trong khoảng 2 021;202 1 để phương trình 2 x 1 m x 2 6.2 7
48 .2 2m 16m 0 có hai nghiệm x , x thỏa mãn x .x 15? 1 2 1 2 A. 1997 . B. 1996 . C. 2021. D. 2020 . Lời giải FB tác giả: Bá Thắng Đặt 2x t ,t 0.
Khi đó phương trình đã cho trở thành 2 t m 2 3 7
48 .t 2m 16m 0 * . t 2m 8 m t 3
Yêu cầu bài toán phương trình
* có hai nghiệm dương và thỏa mãn m log 2m 16 .log 15 . 2 2 3 m 25 48 m 5 0 m 25 48
Phương trình * có hai nghiệm dương S 0 m 48 . 1 7 8 m P 0 5 m 8 m 0 m
Ta có hàm y f m log 2m 16 .log
luôn đồng biến và có f m 15 f 24 suy ra 2 2 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 18
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 m 24 2.
Từ (1) và (2) và giả thiết m 2021;20
21 , m Z m 25;26;.....202 0 .
Có 1996 giá trị nguyên của m thỏa mãn bài toán.
Câu 29: [Mức độ 4] Cho hình lăng trụ ABC.A' B 'C ' có 0
BAC 60 , AC 120, AB 40 và khoảng cách
giữa hai đáy là 45 . Biết hình chiếu của A' lên mặt đáy ABC là điểm H thuộc cạnh BC .
Hai mặt phẳng ABB ' A', ACC ' A' cùng tạo với mặt đáy góc bằng nhau. Khoảng cách giữa
hai đường thẳng AB ' và A'C gần nhất với số nào sau đây? A. 10 . B. 7 . C. 32 . D. 21 . Lời giải FB tác giả: Toàn Hoàng
Gọi O, I lần lượt là trung điểm của A' B, BC A 'C // AOI .
Do hai mặt phẳng ABB ' A', ACC ' A' cùng tạo với mặt đáy góc bằng nhau nên H là chân
đường phân giác trong của góc A . HC AC Ta có
3 H là trung điểm của BI . HB AB A' H
Gọi G A' H OI GH 15 . 3
Khi đó d A'C, AB ' d C, AIG 2d H , AIG .
Gọi M , N lần lượt là hình chiếu của H lên AI, MG HN AIG .
Theo định lý Cosin trong tam giác ABC có BC 40 7 .
Theo công thức độ dài đường trung tuyến có AI 20 3 . 1 S S 30 3 Ta có HM d , B AI ABI ABC . 2 AI 2AI 13 1 1 1
Trong tam giác vuông GHM có HN 6 3 2 2 2 HN HG HM
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 19
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Vậy d A'C, AB ' 2HN 12 3 21. x e 1 ; x 0
Câu 30: [Mức độ 3] Cho hàm số f x
. Biết rằng hàm số f x liên tục trên 2
2x x 3 2 ; x 0 e f ln x và tích phân dx ae b 3 c với a, ,
b c . Giá trị a b 9c bằng x 1 e A. 69 . B. 33 . C. 13 . D. 25 . Lời giải
FB tác giả: Huỳnh Nguyễn Luân Lưu Ta có e f ln x e 1 1 0 1 dx f
ln xd ln x f tdt f xdx f xdx f xdx. x 1 1 1 1 1 0 e e Mặt khác: 0 0 0 0 0 0 x f x dx 2x x 3 2dx 2 x 3 dx 2dx 2 x 32 2 2 2 .d 2x 3 2dx 2 1 1 1 x 3 1 1 1 x 3 03 2 x 0 16 10 2 2 2 3 2 3 . 1 3 3 3 1 1 1
x 1 x f x dx e dx e x1 e 1 1 e . 0 0 0 e f ln x 10 10 Suy ra dx e 2 3 a 1;b 2;c a b 9c 33 . x 3 3 1 e
Câu 31: [Mức độ 3] Cho hàm số 3 2
y x mx 3x 1 C và điểm M 1; 2
. Biết có hai giá trị m là
m và m để đường thẳng : y x 1 cắt đồ thị C tại ba điểm phân biệt A0; 1 , B và C 1 2
sao cho tam giác MBC có diện tích bằng 4 2 . Hỏi tổng 2 2
m m thuộc khoảng nào trong các 1 2 khoảng sau đây? A. 3;5 . B. 15;17 . C. 16;18 . D. 31;33 . Lời giải FB tác giả: Lê Văn Quý
Phương trình hoành độ giao điểm của đồ thị hàm số C và đường thẳng : 3 2
x mx 3x 1 x 1 x 0 3 2
x mx 2x 0 2 x mx 2 0 (1)
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 20
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Đường thẳng : y x 1 cắt đồ thị C tại ba điểm phân biệt
phương trình (1) có hai nghiệm phân biệt khác 0 2 m 8 0 m 2 2 (*). 2 0 m 2 2
Do vậy điều kiện (*) thì đường thẳng : y x 1 cắt đồ thị C tại ba điểm phân biệt A0; 1 , B và C .
Giả sử B x ; x 1 , C x ; x 1 , với x , x là hai nghiệm của phương trình (1). 2 2 1 1 1 2
Theo định lý Vi-ét ta có: x x ; m x x 2 . 1 2 1 2 1 Ta có S d M BC BC M BC ; . 2 1 1 2 1 4 2
. x x 2 x x 2 1 2 1 2 2 2 2 2 x x 2 1 2
2 2 x x 2 4x x 1 2 1 2 2 2 2 m 8 2 8 m 8 m 4
(thỏa mãn điều kiện (*)).
Do đó có hai giá trị trị m là m 4 và m 4 thỏa mãn yêu cầu bài toán. 1 2 Vậy 2 2 m m 32 31;33 . 1 2
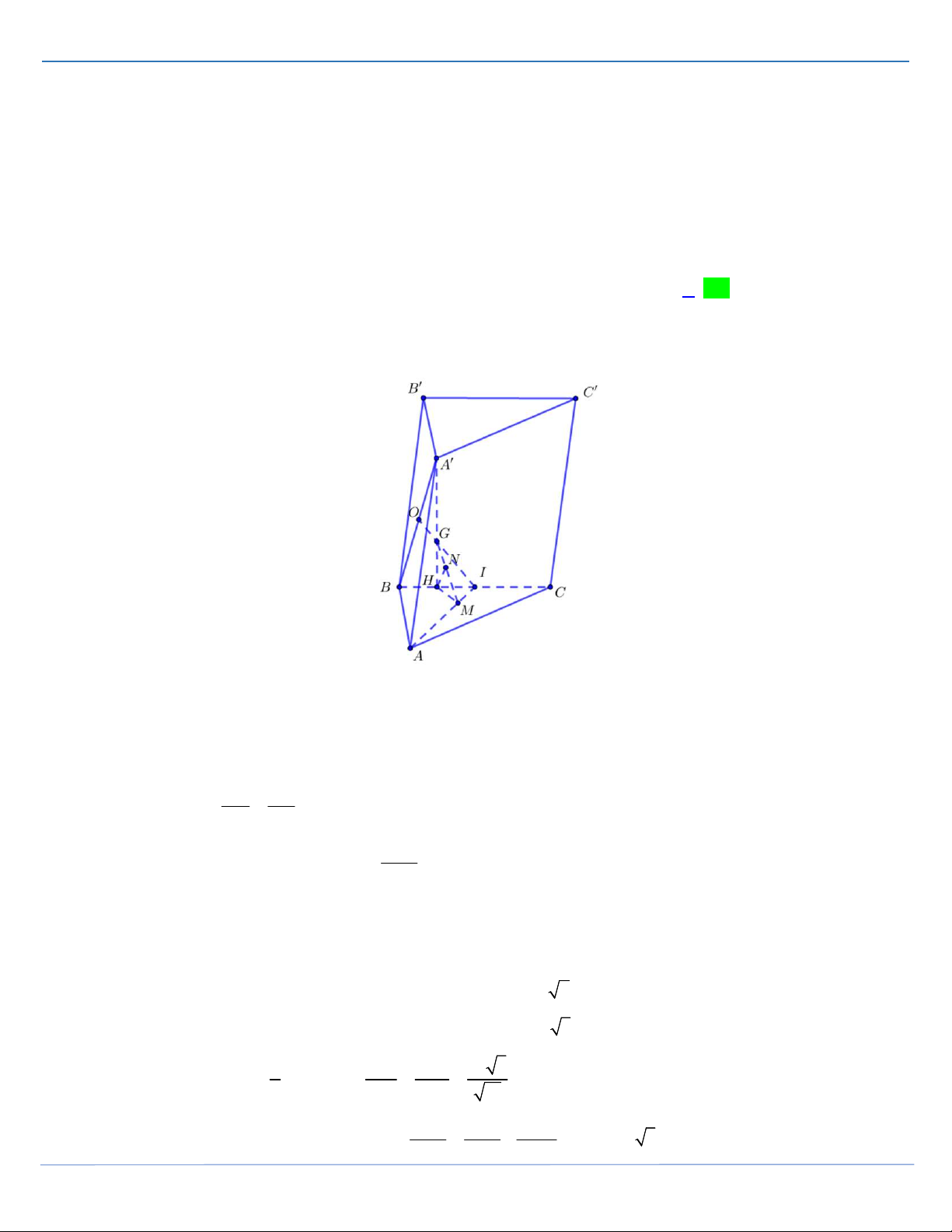
Câu 32: [Mức độ 4] Cho hình lăng trụ ABC .
D A' B 'C ' D' có đáy ABCD là hình chữ nhật với
AB 6, AD 3, A'C 3 và mặt phẳng ACC ' A' vuông góc với đáy. Biết hai mặt phẳng 3
ACC ' A' và ABB' A' tạo với nhau góc với tan . Thể tích V của khối tứ diện 4 BDA'C ' là 8 16 A. V 16. B. V 8 . C. V . D. V . 3 3 Lời giải FB tác giả: Toàn Hoàng
Gọi H là hình chiếu của B lên AC . 2 HA AB Khi đó
2 nên H là trọng tâm tam giác BCD . Khi 2 HC BC đó BH ACC 0
' , BH 2, 90 BH, ABB '
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 21
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 d H, ABB ' 3 2 Suy ra cos d C, ABB' cos . BH 2
Gọi K là trung điểm của AA' CK AA' d C, ABB ' 3 2 sin CK cot 2 2 CK 2 CK.AA' 4 2 AA' 2 A' I
với I là hình chiếu của A' lên AC . AC 3 1 8 Ta có V V . A'C ' BD 3 3
Câu 33: [ Mức độ 3] Cho hàm số y f x có đạo hàm 3 2
f x ax bx cx d ( a,b, c, d là các số
thực). Hàm số y f x có đồ thị như hình vẽ bên và f
1 0 . Số điểm cực tiểu của hàm số
g x f 1 2x f 2 x là A. 3. B. 5. C. 2. D. 4. Lời giải FB tác giả: Toàn Hoàng 4 2 x x
f x ax x x a 3 1 1
x x f x a c . 4 2 Theo bài f
1 0 a 4c x 0 f x c x 2 2 1 . g x 2
f 1 2x f 2 x f 1 2x f 2 x 2.c 2 x 2 1 .4 . c 1 2x 2
x2 2x c 2 x 2 2 2 1 .4 .
c 2 x1 x3 x =4.4c .2 . x x 3 x 3 2 2 1 4x 11x 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 22
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 x 0 x1 x 1 x3 x 3 x5 g x 0 11 73 . x x4 8 11 73 x x2 8
Lập bảng xét dấu ta có x -∞ x1 x2 x3 x4 x5 +∞ g'(x) - 0 + 0 - 0 + 0 - + 0 2 2
Câu 34: [ Mức độ 4] Xét các số thực dương x , y thỏa mãn 2 2 2 4(x y 4) log (xy 4) . 2 x y
Khi x 4 y đạt giá trị nhỏ nhất, giá trị của x 2y bằng A. 0 . B. 9 . C. 9 . D. 6 . Lời giải Tác giả FB: Việt Thịnh Ta có 2 2 2 2 2 4(x y 4) log (xy 4) 2 x y 2(x y) 2 2
4(x y) 8xy 16 log (xy 4) 2 xy 2 2
[2(x y)] log 2(x y) (xy) log (xy). 2 2 Xét hàm số 2
f (t) t t,t 0 f ( t) 2t 1 0, t
0 f (t) đồng biến trên (0;).
Do đó f [2(x y)] f (xy) 2(x y) xy (*) . xy 4(tm)
Nhận xét xy 2(x y) 4 xy xy 4 xy 0 . xy 0(l)
Đặt P x 4 y x P 4 y thay vào (*) ta có 2
2(P 4y y) y(P 4y) 4y (6 P)y 2P 0. (**)
Xét bài toán phương trình (**) phải có nghiệm. P 18 Ta có 2 2
(6 P) 32P 0 P 20P 36 0 . P 2
Mặt khác lại có P x 4y 4 xy P 16 . 2(x y) xy x 6
Vậy x 4 y đạt giá trị nhỏ nhất bằng 18 khi x 2y 0. x 4y 18 y 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 23
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Câu 35: [Mức độ 4] Cho hai hàm số bậc ba y f x, y g x có đồ thị như hình vẽ.
Biết rằng x 1, x 3 đều là các điểm cực trị của hai hàm số y f x, y g x đồng thời 3 f
1 g 3 1, 2 f 3 g
1 4 và f 2x 7 g 2x 3 1. Gọi M , m lần lượt là giá trị
lớn nhất, giá trị nhỏ nhất của hàm số S x 2 f x g x 2 .
g x 27 f x 4g x 2 trên
đoạn 1;3 . Tính M m. A. 2 25. B. 1 84. C. 1 54. D. 1 70. Lời giải FB tác giả: Toàn Hoàng Từ f 2
x 7 g 2x 3 1: f 3 5
+ Thay x 2 vào ta được f 3 g
1 1 kết hợp với 2 f 3 g 1 4 . g 1 6 f 1 1
+ Thay x 3 vào ta được f
1 g 3 1, kết hợp với 3 f 1 g 3 1 . g 3 2
Ta có f x a x x f x a 3 2 3 1 3
x 6x 9x b qua 1;
1 ,3;5 a 1,b 5 f x 3 2 x 6x 9x 5 . Tương tự có g x 3 2 x 6x 9x 2 .
Đặt t f x1;5,x 1; 3 g x 7 t . Xét S x ht 3 2
t 6t 9t 75, t 1;5 . t 1 Ta có ht 2
3t 12t 9 0 . t 3
max S x max ht 75 1; 3 1;5 M 75 M m . min S x min ht 170 9 5 m 95 1; 3 1;5
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 24
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 Vậy M m 1 70 .
Câu 36: [ Mức độ 3] Cho hàm số 3 2 y x x 2 m 2 8
11 x 2m 2 ( m là tham số). Có bao nhiêu giá
trị nguyên của tham số m để đồ thị hàm số có hai điểm cực trị ở về hai phía của trục Ox ? A. 8 . B. 5 . C. 7 . D. 6 . Lời giải FB tác giả: Loan Minh
Hai điểm cục trị của đồ thị hàm số 3 2 y x x 2 m 2 8
11 x 2m 2 ở về hai phía của trục
Ox khi và chỉ khi đồ thị cắt trục hoành tại 3 điểm phân biệt hay phương trình 3 2 x x 2 m 2 8
11 x 2m 2 0 1 có 3 nghiêm phân biệt. Có 3 2 2
x x x m x x 2 2 1 8 11 2 2 0 2 x 6x 1 m 0 x 2 . 2 2 x 6x 1 m 0 * Phương trình
1 có 3 nghiệm phân biệt khi và chỉ khi phương trình * có hai nghiệm phân 0 2 10 m 0 10 m 10 biệt khác 2 . x 2 2 9 m 0 m 3 Do m nguyên nên m 2 ; 1 ;0;1;
2 . Vậy có 5 giá trị nguên của tham số m thỏa mãn yêu cầu bài toán.
Câu 37: [ Mức độ 3] Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2
y 3x 4x 12x m nghịch biến trên khoảng ; 1 ? A. 3. B. 4 . C. 6 . D. 5. Lời giải FB tác giả: Quang Trần x 0 Xét f x 4 3 2
3x 4x 12x m có f x 3 2
12x 12x 24x ; f x 0 x 1 x 2 Bảng biến thiên
Ta thấy hàm số y f x nghịch biến trên ;
1 khi 5 m 0 m 5
Do m và m 10 nên ta có m5;6;7;8; 9 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 25
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
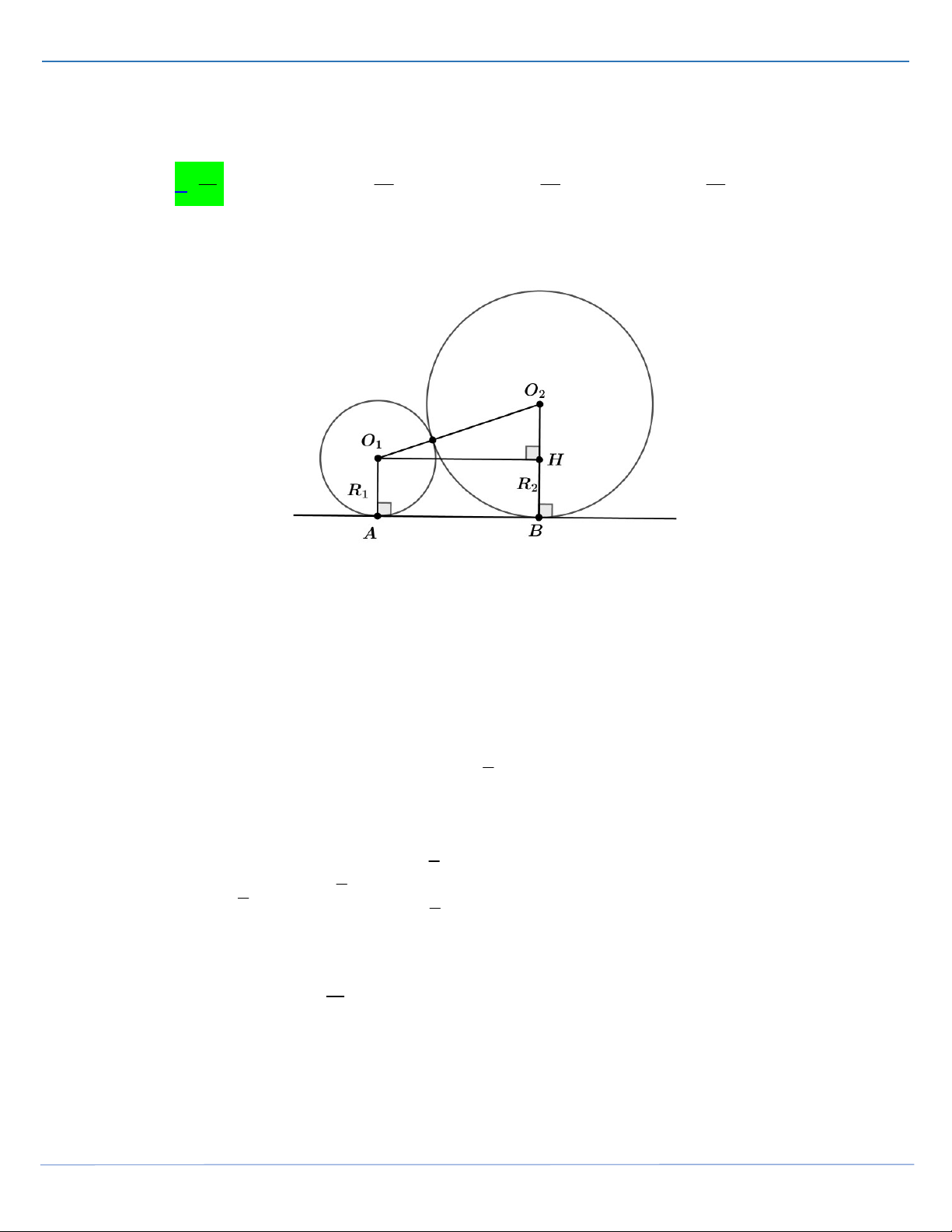
Câu 38: [Mức độ 3] Cho ba mặt cầu S , S , S có bán kính lần lượt là R , R , R đôi một tiếp xúc 1 2 3 1 2 3
với nhau và cùng tiếp xúc với mặt phẳng P . Các tiếp điểm của ba mặt cầu với mặt phẳng
P lập thành một tam giác có độ dài ba cạnh lần lượt là 2,3,4 . Tính tổng R R R ? 1 2 3 61 59 67 53 A. . B. . C. . D. . 12 12 12 12 Lời giải FB tác giả: Quang Trần. Gọi ,
A B,C lần lượt là tiếp điểm của các mặt cầu S , S , S với mặt phẳng P . Không 1 2 3
mất tính tổng quát, giả sử AB 2, BC 3, AC 4 .
Gọi H là hình chiếu vuông góc của O trên O B . Khi đó ta có 1 2
R R 2 O O O H O H AB R R 2 2 2 2 2 1 2 1 2 1 2 2 1 Suy ra 2 4R R AB hay R R 1. 1 2 1 2 9
Tương tự ta cũng chứng minh được R R , R R 4 . 2 3 4 1 3 Ta có R R 1 1 2 4 R R 1 R 1 2 1 9 3 9 R R 2 3 R R 4 3 . 2 3 4 R 2 R R 4 1 3 4 R R 4 1 3 R R R 3 R 3 3 1 2 3 61 Suy ra R R R . 1 2 3 12
Câu 39: [Mức độ 3] Cho hai hàm số bậc ba y f x và y g x f mx n , (trong đó m,n)
có đồ thị như hình vẽ bên. Biết rằng điểm cực tiểu của hàm số y g x lớn hơn điểm cực đại
của hàm số y g x là 5 đơn vị và g0 1
. Khi đó giá trị biểu thức P 3m 2n là
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 26
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 16 19 11 4 A. . B. . C. . D. . 5 2 2 5 Lời giải
FB tác giả: Cao Bá Duyệt
Do y f x là hàm số bậc ba nên 3 2
f x ax bx cx d ; f x 2 3ax 2bx c f 0 1 a 1 f 2 3 b 3 Theo đồ thị ta có: . f 0 0 c 0 f d 1 2 0 Do đó f x 3 2 x 3x 1.
Ta có g x f mx n g x mx n3 mx n2 3 1 n 1 TM Do g 0 1 3 2 n 3n 1 1
n 1 3 L. n 1 3 L
g x mx 3 mx 2 3 3 1 3
1 1 m x 3mx 2 .
Dựa vào đồ thị hàm số g x thì m 0 m . 1 x 3 3 2 2 3 3 0 1 m g x m x m m x . 1 x m 1 x CD Do m 0 m . 1 x CT m 2
Theo bài ra ta có: x x 5 2 5 m . CT D C m 5 6 16
Vậy P 3m 2n 2 . 5 5 2x 1
Câu 40: [Mức độ 3] Cho hàm số y
C và điểm M C . Tiếp tuyến của C tại M cắt x 1
đường tiệm cận ngang của đồ thị tại điểm A . Hỏi có bao nhiêu điểm M thuộc đồ thị C có
tọa độ là các số nguyên để điểm A cách gốc tọa độ một khoảng nhỏ hơn 2 10 ? A. 4 B. 6 C. 5 D. 3.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 27
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 Lời giải
Tác giả: Nguyễn Văn Khoa; Fb: Khoa Nguyen TXĐ: D \ 1 . 3 y . x 2 1 2x 1 Giả sử 0 M x ;
C , x 1, x . 0 x 1 0 0 0 3 2x 1
Tiếp tuyến của C tại M : y x x . 2 0 0 x 1 x 1 0 0
Đường tiệm cận ngang của đồ thị C : y 2 . 3 2x 1 Xét phương trình: 2 x x
2 x 1 3 x x 2x 1 x 1 2 2 0 0 0 0 0 0 x 1 x 1 0 0 x 2x 1. 0
Tiếp tuyến cắt tiệm cận ngang tại điểm A2x 1;2 . 0 5 7
Ta có OA 2 102 OA 40 2x 2 2
1 4 40 x . 0 0 2 2 Do x , x 1 x 2 ;1;0;2;3 . 0 0 0
Do tọa độ điểm M là các số nguyên nên M 2; 1 , M 0; 1 , M 2;5 .
Câu 41: [ Mức độ 4] Cho K là tập hợp các số tự nhiên có bốn chữ số, chọn ngẫu nhiên một số từ K .
Tính xác suất để số được chọn có tổng các chữ số là bội của 4. 2243 2226 2250 2249 A. . B. . C. . D. . 9000 9000 9000 9000 Lời giải Fb tác giả: Lê Minh Huệ
Không gian mẫu có 9000 phần tử.
Gọi số có 4 chữ số mà tổng các chữ số chia hết cho 4 là abcd .
Xét nhóm các chữ số khi chia cho 4 có 4 nhóm khác nhau về số dư 0,4, 8 ,1,5, 9 ,2, 6 ,3, 7 . TH1: a 9 Lập số bcd có 3 10 cách.
Tiếp theo chọn a sao cho a b c d 4 có 2 cách. Có 2000 số.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 28
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 b 9 TH2: a 9 và b 8 Lập số cd có 2 10 cách.
Chọn b để b c d chia cho 4 dư 3 có 2 cách. Có 200 số. TH3: a 9,b 9 c 8 Nếu
thì chọn d có 10 cách, chọn c có 2 cách. c 9
Nếu c 8thì d chia 4 dư 2 nên có 2 cách chọn.
Nếu c 9 thì d chia 4 dư 1 nên có 3 cách chọn. Có 2.10+2+3=25 số. TH4: a 9,b 8 c 8 Nếu
thì chọn d có 10 cách, chọn c có 2 cách. c 9
Nếu c 8thì d chia 4 dư 3 nên có 2 cách chọn.
Nếu c 9 thì d chia 4 dư 2 nên có 2 cách chọn. Có 2.10+2+2=24 số.
Vậy có 2000+200+25+24=2249 số. 2249 Xác suất cần tìm là . 9000
Câu 42: [Mức độ 3] Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD a 3 . Mặt
bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa
đường thẳng SD và mặt phẳng SBC bằng 1 2 5 13 3 A. . B. . C. . D. . 4 5 4 4 Lời giải FB tác giả: Ngo Yen
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 29
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Gọi H là trung điểm của AB .
Do mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy SH ABCD . d D,SBC Gọi SD,SBC sin . SD
Do AD // SBC d D,SBC d ,
A SBC 2d H,SBC 2HK .
Với K là hình chiếu vuông góc của H lên SB . a 3 a 1 1 1 a 3 a 3 Ta có AH , BH mà HK d D,SBC . 2 2 2 2 2 HK SH BH 4 2 Tam giác SHD vuông tại H 2 2 2 2 2
SD SH HD SH AH AD 2a . d D,SBC 3 13 Vậy sin cos SD 4 4 x 1
Câu 43: [ Mức độ 3] Cho hàm số y
( m là tham số). Tập hợp các giá trị của 2 2x 2x m x 1
tham số m để đồ thị hàm số có bốn đường tiệm cận là
A. m 5;4 \ 4 . B. m 5 ;4 \ 4 . C. m 5 ;4.
D. m 5;4 \ 4 . Lời giải
FB tác giả: Cao Bá Duyệt 1 1 1 1 Ta có lim y và lim y nên đường thẳng y và y là các x 2 1 x 2 1 2 1 2 1
đường tiệm cận ngang của ĐTHS. Nhận xét: Phương trình 2
2x 2x m x 1 0 có nhiều nhất 2 nghiệm.
Do đó để ĐTHS có 4 tiệm cận thì phương trình 2
2x 2x m x 1 0 1 phải có 2 nghiệm phân biệt khác 1. x 1 Ta có 2 2
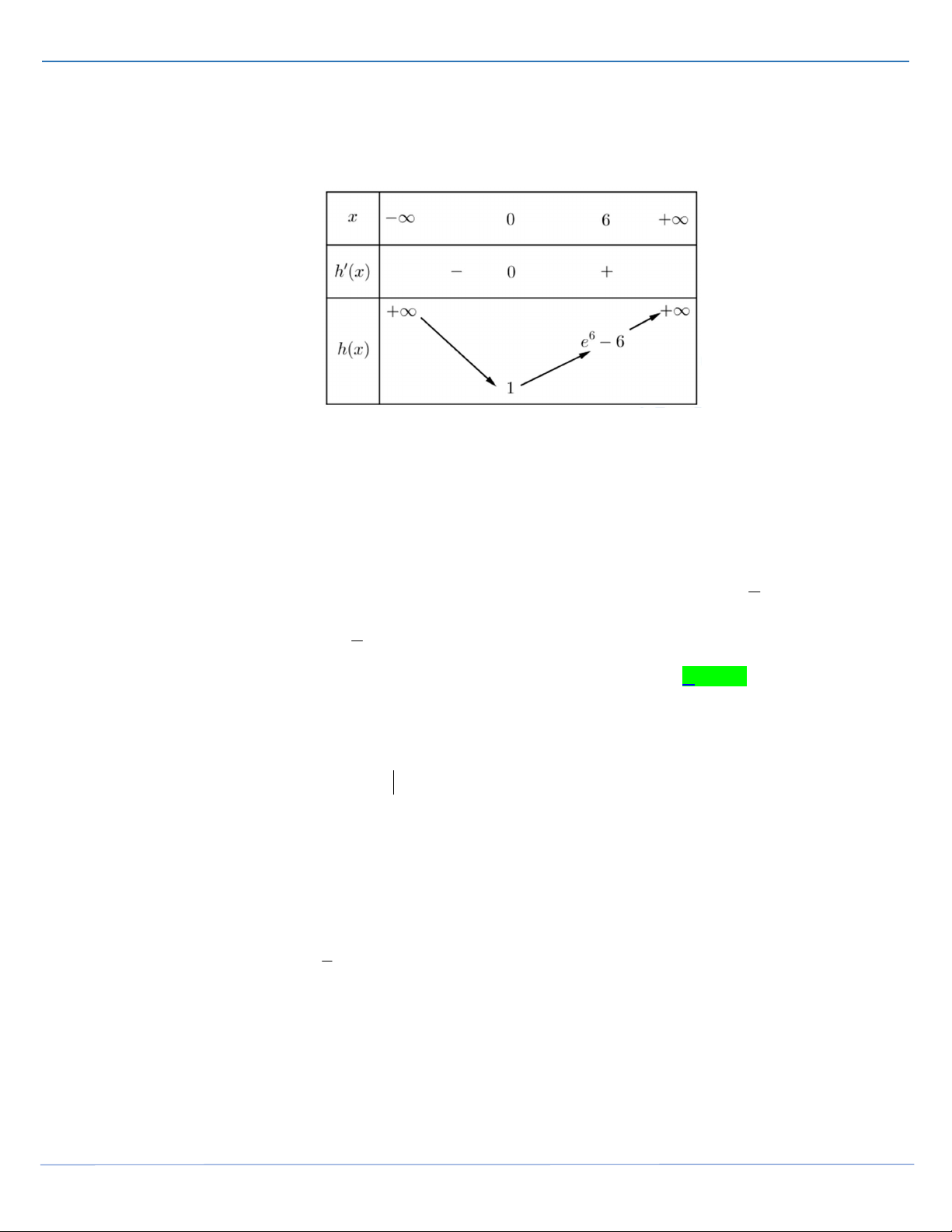
2x 2x m x 1 0 2x 2x m x 1 2x 2xm x 2 2 1 x 1 2 x 4x 1 m Bảng biến thiên hàm 2 y x 4x 1
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 30
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
Từ bảng biến thiên suy ra phương trình
1 có hai nghiệm phân biệt khác 1 khi m 5;4 \ 4
Câu 44: [ Mức độ 4] Có bao nhiêu giá trị nguyên của m thuộc đoạn 0;202 1 để phương trình 3 3 3 ln 3 ln m x x x m m e x m
e có nghiệm lớn hơn 6? A. 2021. B. 1010 . C. 1624 . D. 2020 . Lời giải
FB tác giả: Cao Bá Duyệt Phương trình 3 3 3 ln x 3 . x x m m e
m e ln x m 0 . ln x m a Đặt m b . x e c Từ 3 3 3
a b c 3abc 0 a b c a b2 b c2 c a2 0 a b c 0 ln x m x m e 0 1 a b c ln x m x m e 2 Xét 2 : ln x ln x x x m m e x e e . Xét x
f x x e . Có 1 x f x
e 0 x 0 . Ta có Bảng biến thiên: Do x x e 1 x
. Phương trình ln x x x e e vô nghiệm. Xét 1 : ln x x m m e 0 . x t m e
Đặt ln x m t x t x t
t x e e e x e t . t e x m
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 31
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 Hàm u
g u e u . Có u g u e 1 0 u
g u đồng biến trên
Mà ln x g x g t x t x x m m e x . Xét x
h x e x . Xét x
h x e 1 0 x 0 . Ta có Bảng biến thiên:
Để PT đã cho có nghiệm x 6 thì phương trình h x m có nghiệm x 6 . Từ Bảng biến thiên 6 m e 6 . Mà m0;202
1 ; m nguyên m {398;399;...; 2021} . Có 1624 giá trị của m .
Câu 45: [ Mức độ 3] Cho hàm số y f x có đạo hàm liên tục trên và thỏa mãn điều kiện 1 a
f x f x 2 5 7 1 3 x 2x, x
. Biết rằng tích phân I . x f xdx (với a,b là 0 b a
các số nguyên dương và là phân số tối giản). Tính T 3a b . b A. T 48 . B. T 16 . C. T 0 . D. T 1. Lời giải
FB tác giả: Thành Đức Trung 1 1 1 1 Ta có I xd
f x xf x f
xdx f 1 f xdx 0 0 0 0
Từ điều kiện f x f x 2 5 7 1 3 x 2x, x
Cho x 0 , ta có 5 f 0 7 f 1 0 Cho x 1, ta có 7 f 0 5 f 1 3 Từ đó suy ra f 5 1 8 1 f x 1 dx f 1 xdx 0 0
Cũng từ điều kiện f x f x 2 5 7 1 3 x 2x, x , ta suy ra 1 5 f
x7 f 1 x 1 dx 3x 6x 1 2 dx f xdx 1. 0 0 0
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 32
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 5 3 Ta có I 1 nên a 3,b 8 . 8 8 Vậy T 3a b 1
Câu 46: [Mức độ 3] Cho phương trình 2020 2020 x x 2022 2022 sin cos 2 sin x cos x. Tổng các nghiệm
của phương trình trong khoảng 0; 202 1 bằng 2 12 87 2 12 87 A. . B. 2 643 . C. . D. 2 644 . 2 4 Lời giải
FB tác giả: Trương Thị Tuyến Ta có: 2020 2020 x x 2022 2022 x x 2020 x 2 x 2020 x 2 sin cos 2 sin cos sin 1 2sin cos 12cos x 0 cos2 0 x k x 2020 2020 4 2 sin . x cos 2x cos . x cos 2x 0 , k . 2020 tan x 1 x k 4
Tổng các nghiệm của phương trình là: k . 4 2
Để tổng các nghiệm trong khoảng 0; 20
21 k 0,1,...,128 6 . 2 12 87
Khi đó tổng các nghiệm bằng .1287 1 2...1286 . 4 2 2
Câu 47: [ Mức độ 3] Một tỉnh A đưa ra nghị quyết về giảm biên chế cán bộ công chức, viên chức
hưởng lương từ ngân sách nhà nước trong giai đoạn 2015 2021( 6 năm) là 9,9% so với số
lượng hiện có năm 2015 theo phương thức “ra 2 vào 1”(tức là khi giảm đối tượng hưởng lương
từ ngân sách nhà nước 2 người thì được tuyển mới 1 người). Giả sử tỷ lệ giảm và tuyển dụng
mỗi năm so với năm trước đó là như nhau. Tính tỷ lệ tuyển dụng mới hàng năm(làm tròn đến 0,01% ). A. 1, 72% . B. 2, 06% . C. 1,13% . D. 1,85% . Lời giải
FB tác giả: Trương Thị Tuyến
Gọi x là số cán bộ công chức, viên chức tỉnh A năm 2015 * (x )
r là tỷ lệ giảm hàng năm.
Ta có số người mất việc năm thứ nhất xr
Số người mất việc còn lại sau năm thứ nhất x xr x(1 r)
Tương tự số người mất việc sau năm thứ sáu là 5 x(1 r) r
Suy ra tổng số người mất việc là: 5
xr x(1 r)r ... x(1 r) r 9,9%x
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 33
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 5
r (1 r)r ... (1 r) r 0,099 6 r 1 (1 r) 0,099 6
(1 r) 0,901 r 0,0172 1,72% 1 (1 r)
Tỷ lệ tuyển dụng mới hàng năm chính là tỷ lệ giảm hàng năm.
Vậy tỷ lệ tuyển dụng hàng năm là 1,72%.
Câu 48: [ Mức độ 4] Có bao nhiêu bộ ; x y với ,
x y là các số nguyên và 1 x, y 2021 đồng thởi 2y 2x 1
thỏa mãn điều kiện xy 2x 4y 8log 2x 3y xy 6 log ? 3 2 y 2 x 3 A. 2018.2021. B. 2 . C. 4036 . D. 2018 . Lời giải
FB Tác giả Toàn Hoàng, Kiều Thanh Bình
Cách 1: Thầy Hoàng Thanh Toàn *
x, y : x, y 2021 * x, y : x, y 2021 Điều kiện 2x 1 2y . 0, 0 x 3, y 0 x 3 y 2 2y 2x 1
BPT x 4 y 2.log x 3 2 y .log 3 2 y 2 x 3 x y 2 y 2x 1 4 2 log
log 1 y 2 . x 3 . log log 1 0 3 3 2 2 y 2 x 3
x y 2y y 2 m y x 2x 1 x 3 4 2 . . 2 3 . n 0, , m n 0 y 2 x 3
x 4 y 2m n 0 y 2 y 1 x {4,5,2021} có 4036 bộ số ; x y. y 2
Cách 2: Thầy Kiều Thanh Bình *
x, y : x, y 2021 *
x, y : x, y 2021 + Điều kiện 2x 1 2 y . 0, 0 x 3, y 0 x 3 y 2 x 4 y 2
BPT cho có dạng x 3 y 2log 1 x 4 y 2 log 1 0 (*). 2 3 x 3 y 2 x 4 2
+ Xét y 1 thì (*) thành x 3log 1 3 x 4 log 0 , rõ ràng BPT này 2 3 x 3 3
nghiệm đúng với mọi x 3 vì x x 4 2 3 0, log
1 log 0 1 0, 3 x 4 0, log 0 . 2 2 3 x 3 3
Trường hợp này cho ta đúng 2018 bộ ; x y ; x
1 với 4 x 2021, x .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 34
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
+ Xét y 2 thì (*) thành 4 x 4log 1 0 , BPT này cũng luôn đúng với mọi x mà 3 4 x 2021, x .
Trường hợp này cho ta 2018 cặp ; x y .
+ Với y 2, x 3 thì VT * 0 nên (*) không xảy ra.
Vậy có đúng 4036 bộ số ;
x y thỏa mãn yêu cầu bài toán.
Câu 49: [ Mức độ 3] Cho khối trụ T có hai đáy là hai hình tròn O và O . Xét hình chữ nhật ABCD có hai điểm ,
A B cùng thuộc đường tròn O và hai điểm C, D cùng thuộc đường tròn
O sao cho AB a 3,BC 2a đồng thời mặt phẳng ABCD tạo với mặt đáy của hình trụ
một góc 60 . Thể tích khối trụ T bằng 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. 3 2 a 3 . 3 9 Lời giải
FB tác giả: Việt Thịnh, word Quốc Thép
Gọi A , B lần lượt là hình chiếu vuông góc của ,
A B lên đường tròn O . Dễ thấy ABB A là
hình chữ nhật. Do vậy AB//AB , AB AB 1
Ta có ABCD là hình chữ nhật nên AB//CD, AB CD 2 .
Từ hai điều trên suy ra DCB A
là hình bình hành, nhưng vì tứ giác này nội tiếp đường tròn
Onên nó là hình chữ nhật. Ta có B C
là hình chiếu vuông góc của BC trên AB C D nên ta có: C D B C ABCD, AB C D BC;B C BCB 60 . C D BC BB 2 . a sin 60 a 3 ; h B C 2a cos60 a 2 2
DB DC CB 2a r a 2 3 V r h a 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 35
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022
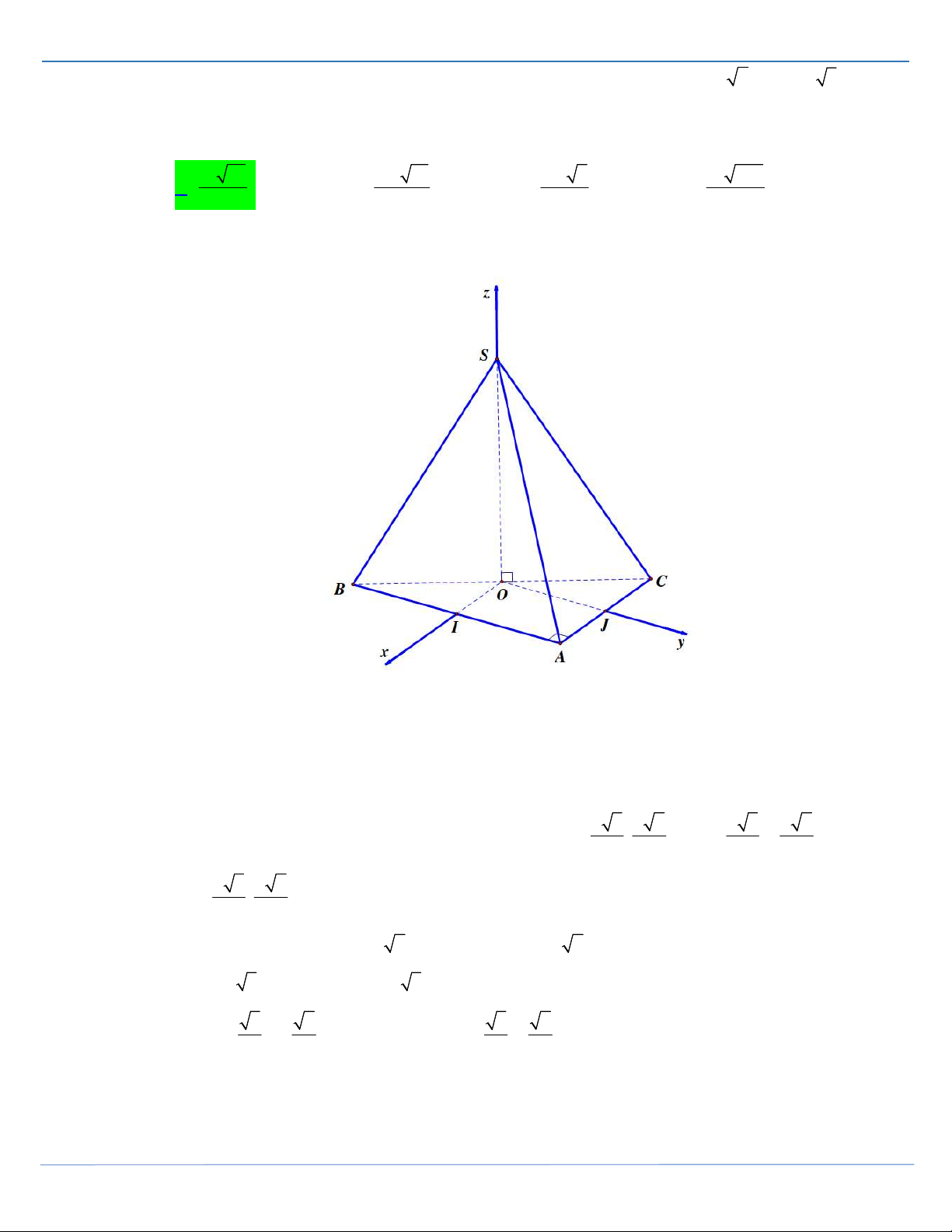
Câu 50: [Mức độ 4] Cho hình chóp S.ABC , có đáy ta giác ABC vuông tại , A AB a 2 , AC a 5 .
Hình chiếu của điểm S trên mặt phẳng ABC trùng với trung điểm của đoạn thẳng BC . Biết
góc giữa mặt phẳng SAB và mặt phẳng SAC bằng 60 . Thể tích của khối chóp S.ABC là 3 a 30 3 5a 10 3 5a 6 3 a 210 A. . B. . C. . D. . 12 12 12 24 Lời giải FB tác giả: Minh Phạm
Ta có SA ABCD suy ra SA CD , cùng với CD AD ta được CD SAD vì vậy góc tạo
bởi SC với mặt phẳng SAD là CSD hay ta có CSD 30 .
Gọi I, J lần lượt là trung điểm của A ,
B AC và O là trung điểm của BC lúc đó ta có OI,OJ,OS
đôi một vuông góc với nhau, do đó ta chọn hệ trục tọa độ Oxyz với Ox,Oy,Oz là các tia trùng a 5 a 2 a 5 a 2
với OI,OJ,OS . Đặt SO ha , tọa độ các điểm A ; ;0, B ; ;0, 2 2 2 2 a 5 a 2 C ; ;0 và S 0;0;ha . 2 2
Tọa độ các vectơ AB 0;a 2;0 .
a u với u 0; 2;0,
AC a 5;0;0 .av với v 5;0;0, 5 2 5 2 AS ; a a; ha . a k với k ; ; h . 2 2 2 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 36
SIÊU PHẨM TỔ 16-STRONG TEAM
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN THANH HOÁ 2021-2022 10
Ta có vectơ pháp tuyến của mặt phẳng SAB là n u,k 2 ; h 0; và pháp tuyến 1 2 10
của mặt phẳng SAC là n v, k 0; 5 ; h . 2 2
Theo giả thiết góc giữa hai mặt phẳng SAB và mặt phẳng SAC bằng 60 nên ta có n n 1 2 1 3 h . n n 2 2 1 2 3 1 a 3 1 a 30
Từ đây ta có thể tích khối chóp S.ABC là V . . .a 2.a 5 . 3 2 2 12
_______________ HẾT _______________
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 37
Document Outline
- ĐỀ-ĐÁP ÁN CHI TIẾT HSG THANH HOÁ 2021-2022
- trang cuoi




