Đề thi học sinh giỏi tỉnh Toán 12 năm 2020 – 2021 sở GD&ĐT Nghệ An (Bảng A)

HƯỚNG DẪN GIẢI
Câu 1a. Cho phương trình sin x = (cot x + 2 3)cos x . Hỏi phương trình đã cho có bao nhiêu
nghiệm thuộc khoảng (0;2020π ) Lời giải
Điều kiện sin x ≠ 0 ⇔ x ≠ kπ , k ∈ . π
Ta có x = + kπ không thỏa mãn phương trình đã cho. 2 π
Xét x ≠ + kπ , phương trình sin x = (cot x + 2 3)cos x ⇔ tan x = cot x + 2 3 2 1 tan x = 2 − + 3 2 ⇔ tan x =
+ 2 3 ⇔ tan x − 2 3 tan x −1 = 0 ⇔  tan x tan x = 2 + 3  π x = + mπ  12 ⇔  (1) với , m n∈ .  5π x = + nπ  12 Xét 1 5 1 + m =
+ n ⇔ m = n + (*) với ,
m n∈ nên phương trình (*) vô nghiệm. Suy ra các 12 12 3
nghiệm của hệ (1) là khác nhau.  π 0 < + mπ < 2020π  1 1  − < m < 2020 − 
Do x ∈(0;2020π ) nên ta có 12  ⇔ 12 12   5π 0 < + nπ < 2020π  5 5  − < n < 2020 −  12  12 12 Suy ra m∈{0;1;2; } ...2019 và n∈{0;1;2; } ...2019 .
Vậy phương trình đã cho có tất cả 4040 nghiệm. ( 2
 4x + )1 x +( y −3) 5− 2y =  0 (1)
Câu 1b. Cho hệ phương trình:  2 2
4x + y + 2 3− 4x = m (2)
( x, y∈  , m là tham số). Tìm tất các các giá trị nguyên của tham số m để hệ phương trình có nghiệm. Lời giải  3 x ≤  Điều kiện:  4  (*) 5 y ≤  2 3 Ta có: 3
⇔ x + x = −( y − ) 3 (1) 4
3 5 − 2y ⇔ (2x) + (2x) = ( 5− 2y ) +( 5− 2y ) (3) Xét hàm số: 3 2
f (u) = u + u ⇒ f '(u) = 3u +1 > 0, u
∀ . Suy ra f (u) luôn đồng biến trên   ≥  ≥
f x = f ( − y ) x 0 x 0 (2 )
5 2 ⇔ 2x = 5 − 2y ⇔  ⇔  Thế vào (2), ta được: 2 2 4x = 5 − 2y 2y = 5 − 4x 2 2  −  2 5 4 4 x x + 
 + 2 3 − 4x = m  2  2 2  −  Xét 2 5 4 ( ) = 4 x g x x +    + 2 3 − 4x với 3 x  ∈ 0; .  2   4    5 2  4 g x x x x  x( 2 x ) 4  3 '( ) 8 8 2 4 4 3 0, x 0;  = − − − = − − < ∀ ∈   2  3 4x 3 4x  4  − − 
Để hệ đã cho có nghiệm  3 g  ⇔ ≤ m ≤ 265 25   g (0) ⇔ ≤ m ≤ + 2 3 .  4  64 4
Vậy các giá trị m nguyên cần tìm là 5,6,7,8,9 . Câu 2.
a) Số phần tử của không gian mẫu: 𝐶𝐶330
Gọi a là biến cố cần tính xác suất.
Giả sử 3 số ghi trên ba quả cầu là a; b; c.
Ta có 𝑏𝑏 = 𝑎𝑎+𝑐𝑐, suy ra a, c cùng chẵn hoặc cùng lẻ. Từ 1 đến 30 cóa 15 số chẵn, 15 số lẻ. 2
Suy ra số kết quả thuận lợi của A là 2𝐶𝐶215. 2
Xác suất cần tính là: 2𝐶𝐶15 𝐶𝐶3 = 3 30 58
b) Cho dãy số (u = = − ∀ ∈ n ) xác định bởi 2 * u 3,u Chứng minh rằng: + u n N n n 2, . 1 1 5(u .u ...u
+ là một số chính phương. n− )2 4 1 2 1 Lời giải Ta có: 2 2 u = − ⇒ = + ⇒ = + + + + u u u + u u u u u u u n n 2 n n 2 ... n 2 2 ... n 2 1 1 ( 1 2 3 )2 ( 2 )( 3 ) ( ) ⇒ 5(u u ...u = u + u + n )2 2 ... n 2 . 1 2 ( 1 ) ( ) Mà 2 u = − = − + + u u u n n 2 n 2 n 2 . 1 ( )( ) Nên u − = − + + = + + + + u u u u u u n 2 2 2 ... n 2 2 2 ... n 2 1 ( 1 )( 1 ) ( ) ( 1 )( 1 ) ( ) ⇒ 5(u u ...u = u − ⇒ + = + = (đpcm) + u u u u + u n )2 n 2 5( ... n )2 2 4 n 2 1 2 1 1 2 1 n Cách 2: u  = 3 1 3± 5
Xét hàm đa thức đặc trưng: 1 2 
⇒ a + = 3 ⇒ a − 3a +1 = 0 ⇒ a = . 2 * u = − ∀ ∈  + u n N a n n 2 2 1 1 2 1 2 4 1
⇒ u = a + ⇒ u = u = a +
⇒ u = u − 2 = a + ... 1 2 1 2 3 2 4 [ ] a a a ( n 1 2 − ) 1 ⇒ u = a + n ( n 1 2 − ) a  1  1  1   n−2 2 4 2 1 ⇒ u u u ...u  = + + + + −  a  a  a   a n ... 1 2 3 1 n−2 2 4 2 a a a a         1   1  1   n−2 2 1 ⇒ a − u u u ...u  = − + +   −  a  a   a n ... 1 2 3 1 n−2 2 a a a a          2 1 = a −  1   n−2 1   n−2 2 2 2 1 a + + ...+ a  + = = −     −   a n .... 2 a 2 n−2 2 2 2 a a a          1 n−2  2 1 ⇒ a − u u u ...u = −   − a 1 2 3 n 1 n−2 2  a  a Mà 1 a − = ± 5 nên a 2 (u u u u   = = − − u u u u −  a − n )2 ( n )2 2 2 1 5. ... 5 ... n 1 2 3 1 1 2 3 1 n−2 2 a    2 2 (  n− 1   n− 1 5. u u u ...u  ⇒ + = − + = − = + (đpcm) −  a −   a −  u n 4 n 4 n n 1 1 2 3 1 ) 2 2 2 2 2 2 2 2 ( ) 2 2  a   a 
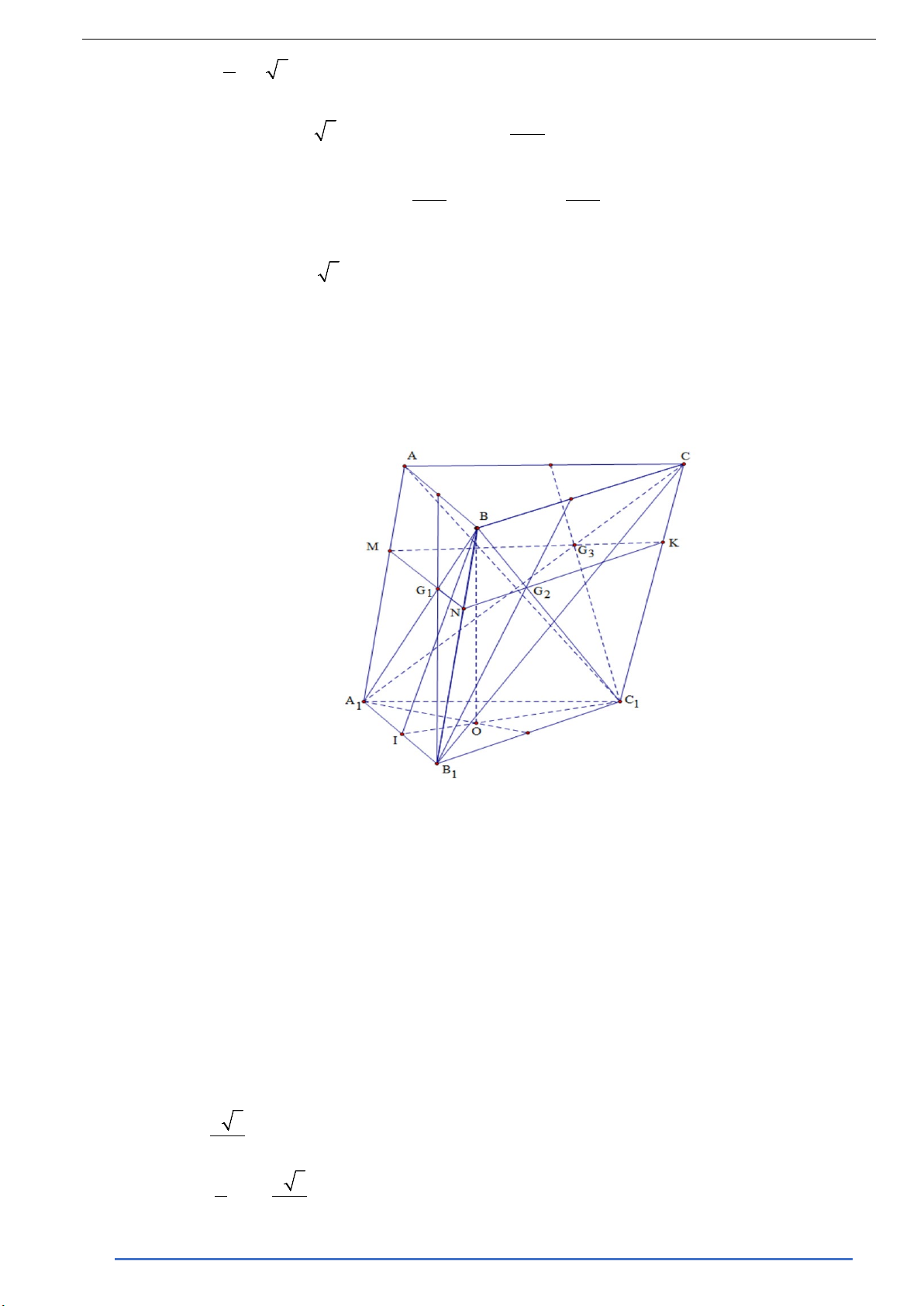
Câu 3. Cho hình lăng trụ AB .
C A B C có đáy là tam giác đều cạnh bằng a và 1 1 1
BA = BB = BC = a 3 . 1 1 1
a) Tính khoảng cách từ C đến mặt phẳng ( ABB A . 1 1 )
b) Gọi G , G , G lần lượt là trọng tâm các tam giác ABB , ACC , CBB . Tính thể tích khối đa 1 2 2 1 1 1
diện lồi có các đỉnh là các điểm G , G , G , A , B và C . 1 2 2 1 1 1 Lời giải
a) Tính khoảng cách từ C đến mặt phẳng ( ABB A . 1 1 )
Gọi O là tâm đường tròn ngoại tiếp A ∆ BC
Gọi I là trung điểm A B . 1 1 A B ⊥ C I 1 1 1 
⇒ A B ⊥ BC I . 1 1 ( 1 ) A B ⊥  BO 1 1
Kẻ C H ⊥ BI . 1
Mà C H ⊥ A B . 1 1 1
⇒ C H ⊥ A B BA . 1 ( 1 1 )
Vì CC // A B BA d ( ,
C ( A B BA = d C , A B BA = C H . 1 1 )) ( 1 ( 1 1 )) 1 ( 1 1 ) 1 A
∆ B C là tam giác đều. Suy ra : 1 1 1 a 3 C I = . 1 2 2 a 3 C O = C I = . 1 1 3 3 1 a 3 IO = C O = . 1 2 6 2 a a 11 2 2 2
BI = BA − A I = 3a − = . 1 1 4 2 2 2 11a 3a 2a 2 2 2
BO = BI − IO = − = . 4 36 3 1 1
C I.BO 2a 2 S
= C I.BO = BI.C H 1 ⇒ C H = = . B ∆ 1 1 IC 1 1 2 2 BI 11 d (C ( 2a 2 , A B BA = . 1 1 )) 11
b) Gọi G , G , G lần lượt là trọng tâm các tam giác ABB , ACC , CBB . Tính thể tích khối đa 1 2 2 1 1 1
diện lồi có các đỉnh là các điểm G , G , G , A , B và C . 1 2 2 1 1 1
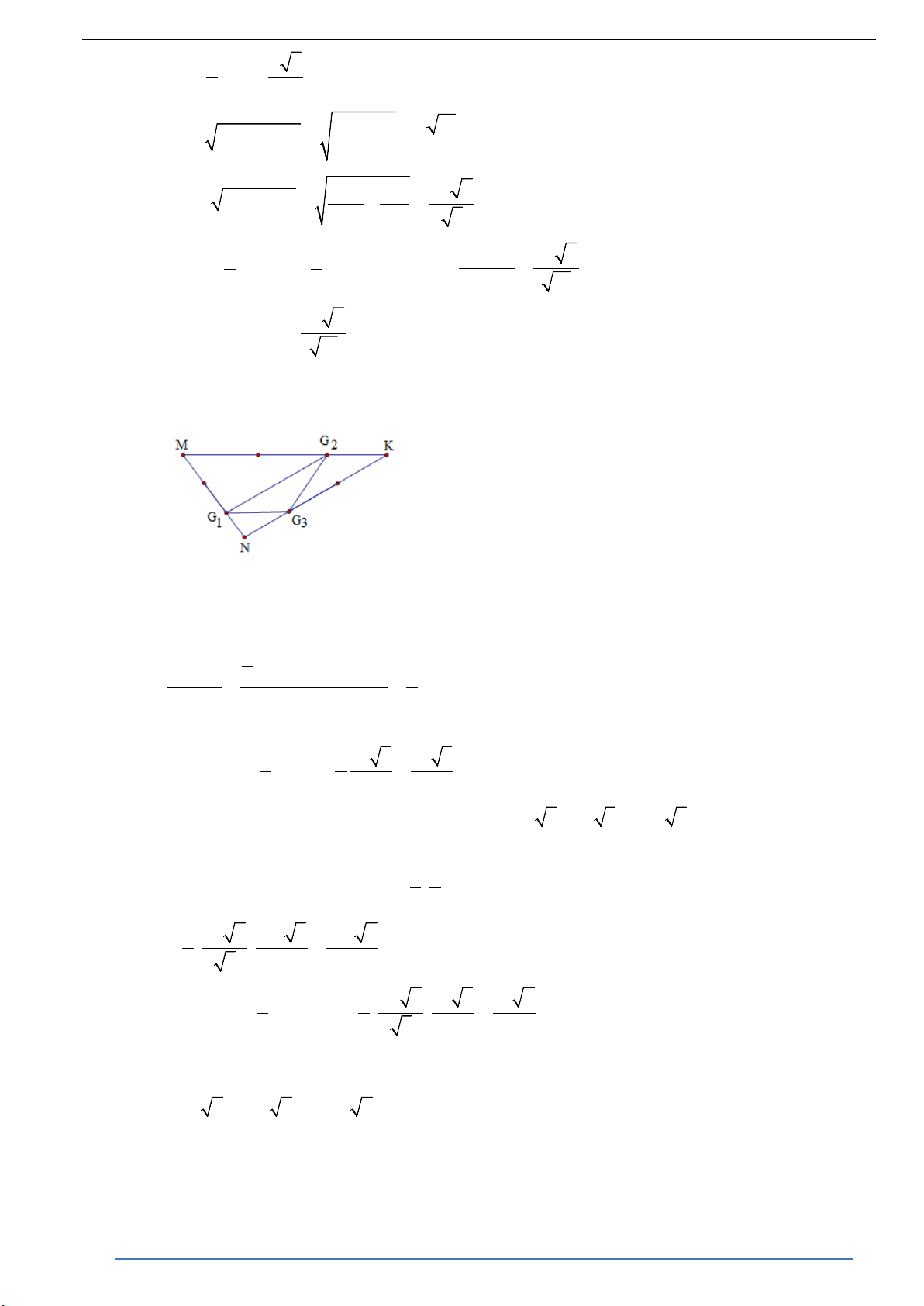
Qua G kẻ đường thẳng song song với AB cắt A A , B B lần lượt tại M và N . 1 1 1
Trong (B C CB gọi K = NG ∩CC ⇒ M,G , K thẳng hàng. 1 1 ) 3 1 2
1 G G .d G ,G G S 1 3 ( 2 1 3) G ∆ G G 2 1 2 3 2 = = S 1 M ∆ NK MK d (N MK ) 9 . . , 2 2 2 2 2 a 3 a 3 ⇒ S = S = = ∆ ∆ 1 G 2 G 3 G 9 MNK 9 4 18 2 2 2 a 3 a 3 7a 3 ⇒ S + S + S = S − S = − = M ∆ ∆ ∆ ∆ ∆ 1 G 2 G K 2 G 3 G N 1 G 3 G MNK 1 G 2 G 3 G 4 18 36 1 2 ⇒ V + V + V = . BO S + S + S  ∆ ∆ ∆   1 A .M 1 G 2 G 1 B .N 1 G 3 G 1 C .K 2 G 3 G M 1 G 2 G K 2 G 3 G N 1 G 3 3 3 G 2 3 2 2a 2 7a 3 7a 2 = . . = . 9 3 36 81 2 3 2 2 2a 2 a 3 a 2 V = B0.S = . . = . ∆ 1 A 1 B 1 C .MNK 3 MNK 3 3 4 3 ⇒ V = V − V + V + V  =   1 A 1 B 1 C . 1 G 2 G 3 G 1 A 1 B 1 C .MNK 1 A .M 1 G 2 G 1 B .N 1 G 3 G 1 C .K 2 G 3 G 3 3 3 a 2 7a 2 20a 2 = − = . 3 81 81
Câu 4. Cho x, y, z là các số thực dương thõa mãn 2x + 4y + 7z = 2xyz .Tìm giá trị nhỏ nhất của biểu
thức P = x + y + z . Lời giải 3 5     3 5 x y
 x   y  7 3 5 7  2   4  = + + = + + ≥     = 15
2xyz 2x 4y 7z 3 5 7z 15 15 z
15 x y z     . 3 5 3 5  3   5      2 4  2   4  3 5 15 3 5 15 15 15 15 15 3 5 7  2   4  12 10 8 15   2   4 2 x y z 15 x y z    x y z  ⇒ ≥ ⇔ ≥  . 3 5  2   3  5           6 5 4 6 5 4 15 x y z
 x   y   z  15 x y z 4 = + + = + + ≥ 15 15 P x y z 6 5 4 15 =       6 5 4 6 5 4  6   5   4  4 6 5 4 6 5 15 3 5 6 5 15 6 5 4  2   4  15
15   2   4   2   4  15 = 15 15 x y z ≥ = 4
 3  5 4  2   3  5  3  5      
         2  x y = =  3 5 z a ≠ 0   1  2 4  a = ± x = 6a   2 15 15  x y z    Vây P ≥ , MinP = ⇔  = = ⇔ y = 5a ⇔ x = 6a 2 2 6 5 4  z = 4a y = 5a
2x + 4y + 7z = 2xyz   3   = z = 4 60 240 a a a   x = 3 x = 3 −  5  − ⇔ 5
y = hoặc y = . 2  2  z = 2  z = 2 − 
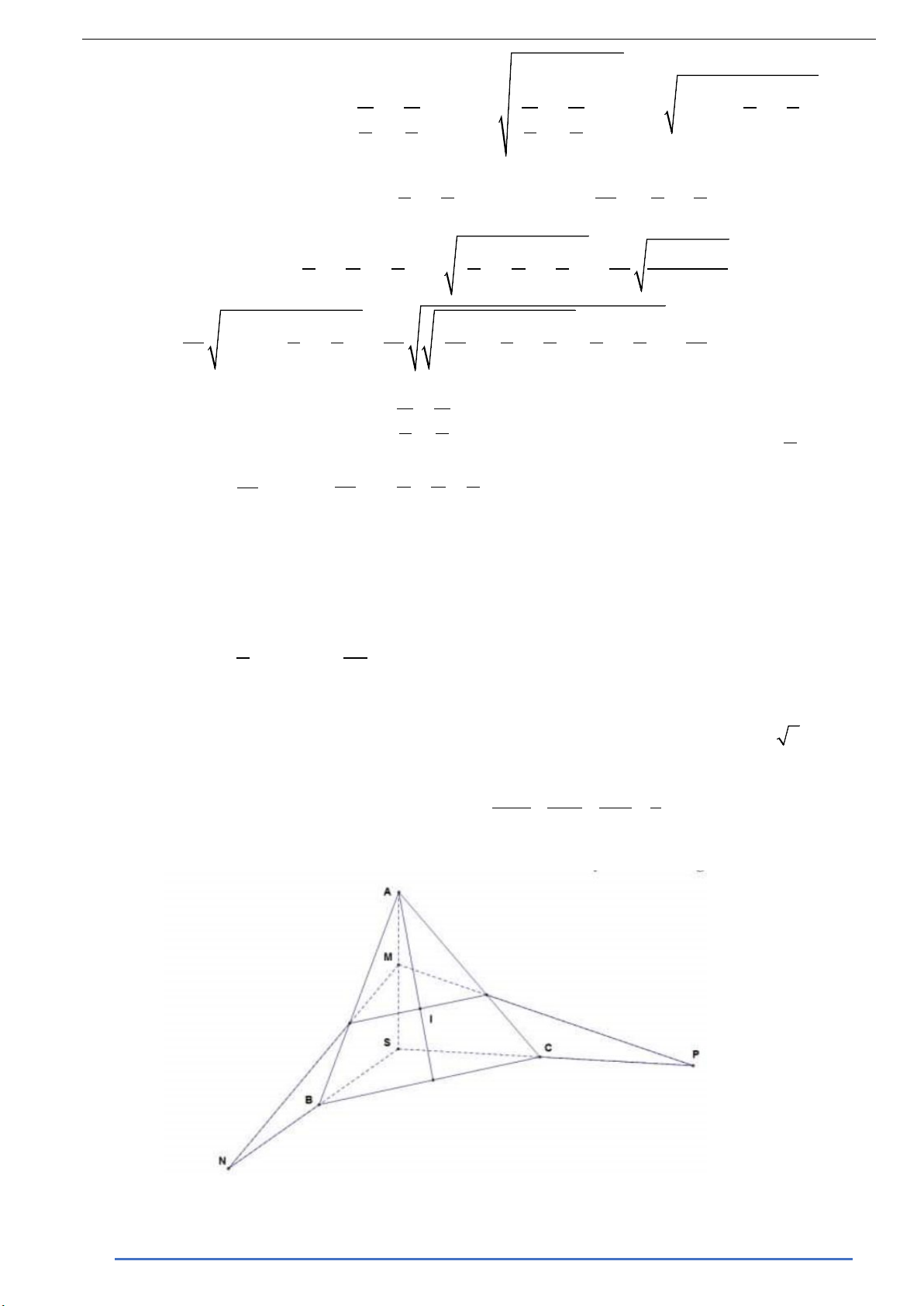
Câu 5. Cho hình chóp S.ABC có ,
SA SB, SC đôi một vuông góc và SA =1, SB = SC = 2 2 . Gọi I là
tâm đường tròn nội tiếp tam giác ABC . Mặt phẳng (α ) thay đổi đi qua I lần lượt cắt các tia ,
SA SB, SC tại M , N, P . Chứng minh rằng 1 1 1 5 + + ≥ . 2 2 2 SM SN SP 8 Lời giải
Trước hết ta chứng minh bài toán: Cho hình chóp S.ABC . Điểm I nằm trong mặt phẳng ( ABC)    
thỏa mãn aIA + bIB + cIC = 0 . Mặt phẳng (α ) đi qua điểm I và cắt các tia ,
SA SB, SC lần lượt
tại các điểm M , N, P . Chứng minh rằng . SA + . SB + . SC a b c
= a + b + c . SM SN SP Thật vậy:           
aIA + bIB + cIC = 0 ⇔ a(SA− SI )+ .b(SB − SI )+ .c(SC − SI ) = 0       . SA . + . SB . + . SC a SM b SN c .SP
 aSA+ bSB + cSC SM SN SP ⇔ SI = = a + b + c a + b + c
Vì M , N, P, I đồng phẳng nên
. SA + . SB + . SC a b c SM SN SP =1⇔ . SA a + . SB b + . SC c
= a + b + c (*) a + b + c SM SN SP    
Ta có: I là tâm đường tròn nội tiếp tam giác ABC nên aIA + bIB + cIC = 0
Từ giả thiết suy ra tam giác ABC có a = BC = 4, b = AC = 3, c = AB = 3 Áp dụng (*) ta được: 1 2 2 2 2 4. + 3. + 3. = 4 + 3+ 3 SM SN SP
Áp dụng bất đẳng thức Buniacopxki ta có: 4 6 2 6 2 ( ) 1 1 1 10 16 72 72  = + + ≤ + + + +  2 2 2 SM SN SP SM SN SP    1 1 1 5 ⇔ + + ≥ 2 2 2 SM SN SP 8 Dấu bằng xảy ra khi 4 2
SM = 4, SN = SP = . 3
____________________ HẾT ____________________
Document Outline

• de-thi-hoc-sinh-gioi-tinh-toan-12-nam-2020-2021-so-gddt-nghe-an-bang-a
• ĐỀ-HSG-Nghệ-An