Đề thi học sinh giỏi tỉnh Toán 12 THPT năm 2019 – 2020 sở GD&ĐT Hưng Yên

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH HƯNG YÊN NĂM HỌC 2019 - 2020 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài 180 phút (không kể thời gian phát đề)
Câu I (6,0 điểm). 1. Cho hàm số 3 2
y  x  mx  1 có đồ thị C . Tìm các giá trị của tham số m để đường thẳng m 
d: y  1x cắt đồ thị C tại 3 điểm phân biệt sao cho tiếp tuyến của đồ thị C tại hai m  m 
trong ba điểm đó vuông góc với nhau. x  2 1 2. Cho hàm số y 
có đồ thị C  . Gọi Ax ;y ,B x ;y là các điểm cực trị của C  1 1   2 2 x  2  
với x  x . Tìm điểm M trên trục tung sao cho 2 2
T  2MA  MB  2MA  MB đạt giá trị nhỏ 1 2 nhất.
Câu II (4,0 điểm). 1 1. Giải phương trình: log 2x  2  log 2x  1 . 1 3   3 2  3   2
2. Cho các số thực a, , b c 2  ;8
   và thỏa mãn điều kiện abc  64. Tìm giá trị lớn nhất của biểu thức 2 2 2
P  log a  log b  log c . 2 2 2
Câu III (5,0 điểm).
1. Cho hình chóp S.ABCD có ABCD là hình thang cân với AD  2a,AB  BC  CD  a , cạnh
SA vuông góc với đáy. Gọi M là trung điểm của SB và N là điểm thuộc đoạn SD sao cho 6a 43
NS  2ND . Biết khoảng cách từ S đến mặt phẳng (AMN) bằng
, tính thể tích của khối 43
chóp S.ABCD theo a.  
2. Cho tam giác ABC vuông tại A có 60o ABC 
. Đường phân giác của góc ABC cắt AC tại I.
Trên nửa mặt phẳng bờ là đường thẳng AC, vẽ nửa đường tròn tâm I tiếp xúc với cạnh BC.
Cho miền tam giác ABC và nửa hình tròn trên quay quanh trục AC tạo thành các khối tròn xoay V
có thể tích lần lượt là V ,V . Tính tỉ số 1 . 1 2 V2 ln x  1
Câu IV (1,0 điểm). Tìm họ nguyên hàm I  dx  .
x ln x  1  1
 x  2  y  2  7y  3x  8 
Câu V (2,0 điểm). Giải hệ phương trình  . 3 2 2
 3xy  8x  5  xy  6x  12y  7  a   1  1 
Câu VI (2,0 điểm). Cho dãy a xác định 
. Tìm số hạng tổng quát a n   2 n 1 a   a  , n  1 n n 1  n  2n và tính lima . n
............HẾT............
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh ...........................................................................Số báo danh .................
Giám thị coi thi ..........................................................................
HƯỚNG DẪN GIẢI THAM KHẢO
Câu I. 1. Cho hàm số 3 2
y  x  mx  1 có đồ thị C . Tìm các giá trị của tham số m để đường m 
thẳng d : y  1  x cắt đồ thị C tại 3 điểm phân biệt sao cho tiếp tuyến của đồ thị C tại m  m 
hai trong ba điểm đó vuông góc với nhau. Hướng dẫn
Giả sử có ba giao điểm là A, B, C khác nhau, phương trình hoành độ giao điểm là: x   0  A 0;1 3 2   
x  mx  x  0  
. Dễ thấy k  0  y  1 suy ra không có tiếp tuyến 2 x
  mx  1  0  * A tt 
vuông góc nhau tại A. Còn lại hai giao điểm B, C có hoành độ là nghiệm của (*). x  x  1  Ta có 1 2 
và để hai tiếp tuyến vuông góc nhau thì x 3x  2m .x 3x  2m  1 1  1  2  2  x   x  m   1 2  2 2 2
 9  6m  4m  1  m  5  m   5 , thỏa mãn 2
  m  4  0 .
Vậy các giá trị của m là m   5 . x  2 1
Câu I. 2. Cho hàm số y 
có đồ thị C  . Gọi Ax ;y ,B x ;y là các điểm cực trị của 1 1   2 2 x  2  
C với x  x . Tìm điểm M trên trục tung sao cho 2 2
T  2MA  MB  2MA  MB đạt giá trị 1 2 nhỏ nhất. Hướng dẫn. 1 1
Ta có y  x 
,x  2  y '  1 
 x  3,x  1 là hoành độ các điểm cực x  2 x  22 1 2  
trị hay A3;4,B 1; 
1 . Gọi I là điểm thỏa mãn 2IA  IB  0  I 5;9. 2 2     2   2 
Khi đó T  2MA  MB  2MA  MB  2MI  I 
A  MI  IB  MI
T  IA  IB  MI  MI    y  2   y  2 2 2 2 2 2 2 2 5 9 5 9  27  5  32 Nên T
 32  y  9  M 0;9 . min   1
Câu II. 1. Giải phương trình: log 2x  2  log 2x  1 . 1 3   3 2  3   2 Hướng dẫn. 2 1 t t PT log 2x  2  log
2x  1  t  2x  2  1  3  3  2 3  1 1 3   3 2  3       2 t t 3 2 3  1     1                  t t
f t  a  b  1  0,0  a,b   1 , ta có 4  2 3    4  2 3  '  t  ln t f t a
a  b lnb  0, t suy ra f t nghịch biên trên  nên f t  0 có nghiệm duy nhất
t  1  x  1  3 là nghiệm duy nhất của phương trình đã cho.
Câu II. 2. Cho các số thực a, , b c 2  ;8
   và thỏa mãn điều kiện abc  64. Tìm giá trị lớn nhất của biểu thức 2 2 2
P  log a  log b  log c . 2 2 2 Hướng dẫn. Đặt log a x, log b , y log c z x, , y z 1  ;3     
,x  y  z  6 2 2 2   . Ta cần tìm GTLN của 2 2 2
P  x  y  z . Không giảm tổng quát ta giả sử 1 x y z 3 x 1;  2,z 2  ;3            .
P  x  z    z  x2 2 2 2
 z    x 2 6 2 2 6
z  36  2x  12x (Parabol đồng biến đối với z vì 6 x x  5   3   2;  ) 2  P     x 2 2 2.3 6 6
 36  2x  12x  2x  6x  18  14 ( tại 2 2  2  
x  1  x  2 ) suy ra P
 14  x  1,y  2,z  3 (loại y  1,x  2,z  3 ). max Vậy P
 14  a  2,b  4,c  8 (và các hoán vị). max
Câu III. 1. Cho hình chóp S.ABCD có ABCD là hình thang cân với
AD  2a,AB  BC  CD  a , cạnh SA vuông góc với đáy. Gọi M là trung điểm của SB và N là
điểm thuộc đoạn SD sao cho NS  2ND . Biết khoảng cách từ S đến mặt phẳng (AMN) bằng
6a 43 , tính thể tích của khối chóp S.ABCD theo a. 43 Hướng dẫn.
Gọi E là trung điểm của AD thì dễ dàng chứng minh được ABCE là hình thoi cạnh a, CDE là tam giác đề a 3
u cạnh a. Kẻ CH vuông góc với ED thì CH 
và là đường cao của hình thang 2 2 3a 3
cân ABCD, suy ra S  . ABCD 4
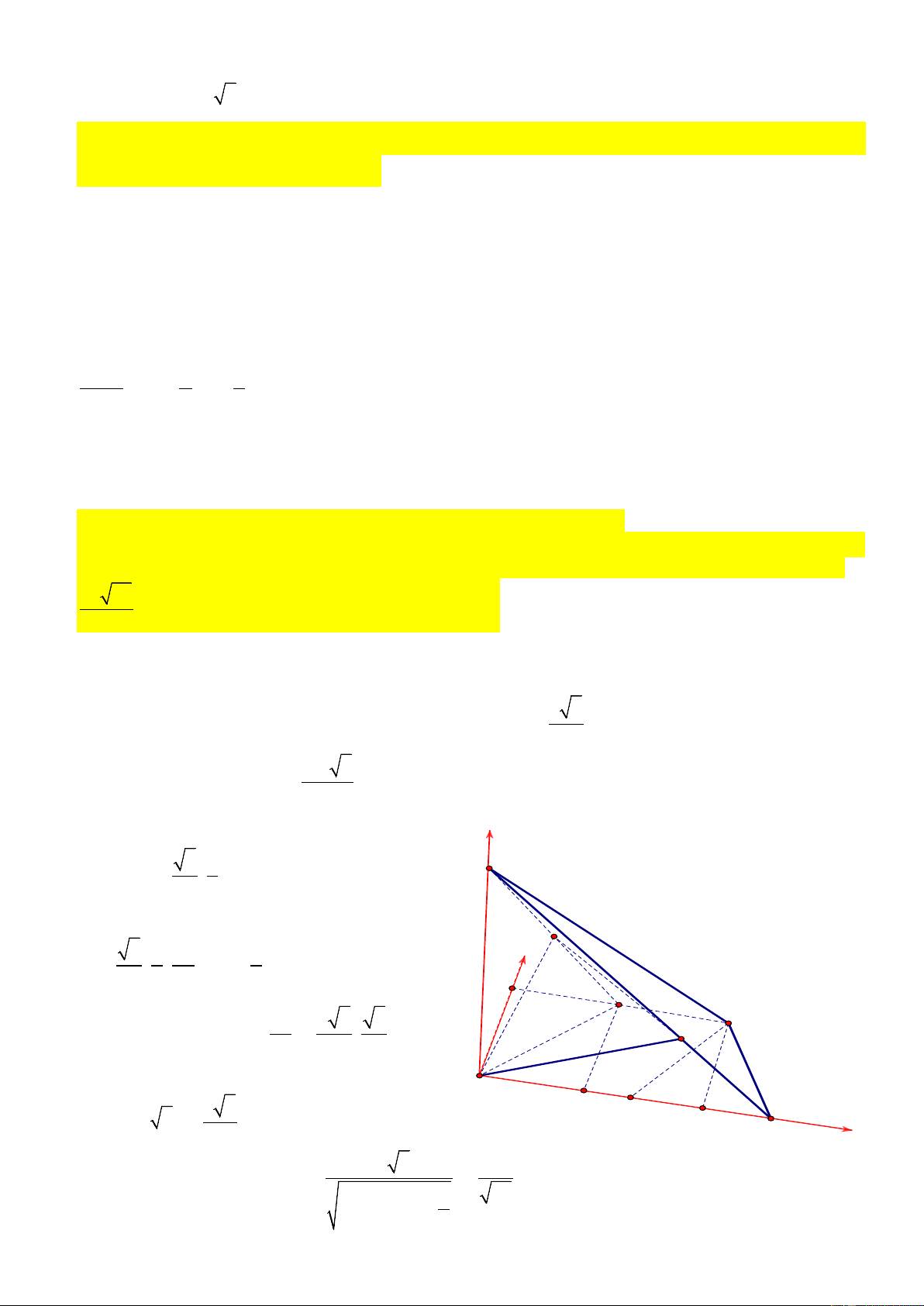
Lấy a = 1. Dựng hệ tọa độ Axyz như hình z  3 1  S vẽ, với B  ; ;0  ,D  
0;2;0,S 0;0;3h,  2 2   
khi đó tọa độ các điểm  M  3 1 3h   2   M  ; ;  
,N 0; ;h. x   4 4 2       3        3h h 3 3  B Ta có AM  ,AN    ; ;    , khi N C    4 4 6   
đó phương trình mặt phẳng (AMN) là A 2 3 E
3hx  h 3y  z  0 H y 3 D 2h 3 6
Khoảng cách d S,AMN    suy ra 2 2 4 43 9h  3h  3     2  2 4 2 2  6 6a 7 43h  3 12
 h    36h  4  h   S 0;0;   SA   hay và thể tích khối chóp  3    7  7  7 2 3 1 6a 7 3a 3 3a 21
S.ABCD là: V  . .  . 3 7 4 14  
Câu III. 2. Cho tam giác ABC vuông tại A có 60o ABC 
. Đường phân giác của góc ABC cắt
AC tại I. Trên nửa mặt phẳng bờ là đường thẳng AC, vẽ nửa đường tròn tâm I tiếp xúc với cạnh
BC. Cho miền tam giác ABC và nửa hình tròn trên quay quanh trục AC tạo thành các khối tròn V
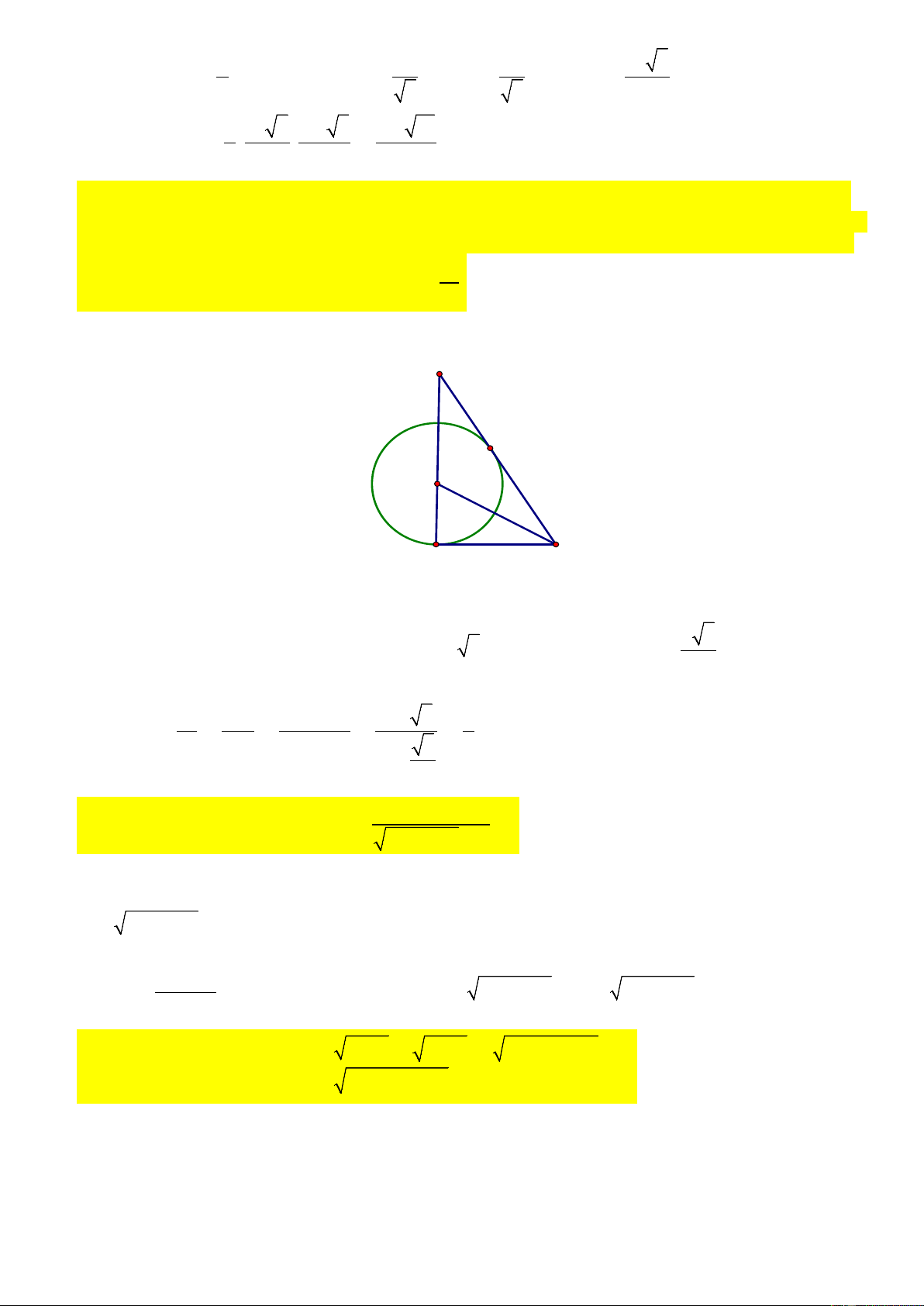
xoay có thể tích lần lượt là V ,V . Tính tỉ số 1 . 1 2 V2 Hướng dẫn. C D I A B
Đặt AB  a , khi đó o o a 3
AC  h  AB tan 60  a 3,IA  R  AB tan 30  . Khi cho tam giác 3
ABC và nửa hình tròn tâm I quay xung xung quanh AC thì tạo thành khối nón tròn xoay và khối 2 2 V V a  h / 3 a .a 3 9 cầu. Ta có: 1 non     . 3 V V 4 R  / 3 cau 3 4 2 3 4.a 9 1  ln x
Câu IV. Tìm họ nguyên hàm I  dx  .
x ln x  1  1 Hướng dẫn. Đặ 2
t x ln x  1  1  t  x ln x  1  t  
1  1  lnxdx  2t   1 dt , suy ra  I t 2t 1 
dt  2t  2 lnt C  I 
x  2 x lnx 1 2ln x lnx 1  1C . t
 x  2  y  2  7y  3x  8 
Câu V. Giải hệ phương trình:  . 3 2 2
 3xy  8x  5  xy  6x  12y  7  Hướng dẫn.
+ Xét x  2 thì từ phương trình đầu ta có y  2 thế vào phương trình thứ hai không thỏa
mãn. Lập luận tương tự đối với y  2 ta suy ra điều kiện x,y  2 .
+ Biến đổi phương trình thứ nhất: y 2 y 2   1   7  
  3  1  t  7t  3,t  0  t  1  x  y  2. x  2 x  2
Thế vào phương trình thứ hai: 3 2 3 2
3x  8x  5  x  6x  12x  7 (*). Đặ 3 t 3 2 2 3
3x  8x  5  t  3x  8x  5  t , từ (*) ta có 3
t  t  x    x   3 1 1  u  u
Hay t  u 2 2
t  tu  u  
1  0  t  u  x  1. Từ đó ta được:
x  x   x  3 2 3 2 3 8 5
1  x  6x  11x  6  0  x  1,x  2,x  3 (thỏa mãn).
Vậy hệ đã cho có ba nghiệm x,y  
 1; 1,2;2,3;3. a   1  1 
Câu VI. Cho dãy a xác định 
. Tìm số hạng tổng quát a và tính n   2 n 1 a   a  , n  1 n n 1  n  2n lima . n Hướng dẫn. n  2
Dễ thấy dãy số đã cho là dãy số dương và tăng. Giả sử a  4 
, n  1 , khi đó ta có: n n 1 2  n  2 n  1 2n  4 n  1 n  3
a  1 đúng, a  4    4    4  (đúng tới n + 1). 1 n 1  n 1 2  2n 2n 2n 2n n  2 n  2 Vậy a  4 
, n  1 . Suy ra lima  lim 4   4  2 . n n 1 2  n n 1 2 
Lời bình: Nhìn chung đề này ở mức độ khá.
............HẾT............
Document Outline

• DE THI HSG 12 TỈNH HƯNG YÊN + HD GIẢI