Đề thi học sinh giỏi tỉnh Toán THPT năm 2020 – 2021 sở GD&ĐT Lào Cai

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THPT LÀO CAI NĂM HỌC 2020 – 2021 TOANMATH.com Môn thi: TOÁN THPT ĐỀ THI CHÍNH THỨC Ngày thi: 18/01/2021
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Đề thi gồm 01 trang – 05 câu Câu 1. (5,0 điểm)
a) Cho hàm số y  f  x liên tục trên  , biết f x   x   x  2 '( ) 2 4 , x
   . Xét tính đơn điệu của hàm số y  f  2 x  3x .
b) Cho hàm số y  f  x   x   x  2 2 1 , x
   . Tìm tất cả các giá trị của tham số m để đồ thị hàm số 2
y  f  x  2 f  x  m có 9 điểm cực trị. Câu 2. (4,0 điểm) x x
a) Giải bất phương trình 2  3  2.2  3 1.
b) Tìm tất cả các giá trị của tham số m để phương trình log 2x  m 2
 2log x  x  4x  2m 1 có hai 2 2 nghiệm thực phân biệt. Câu 3. (5,0 điểm)
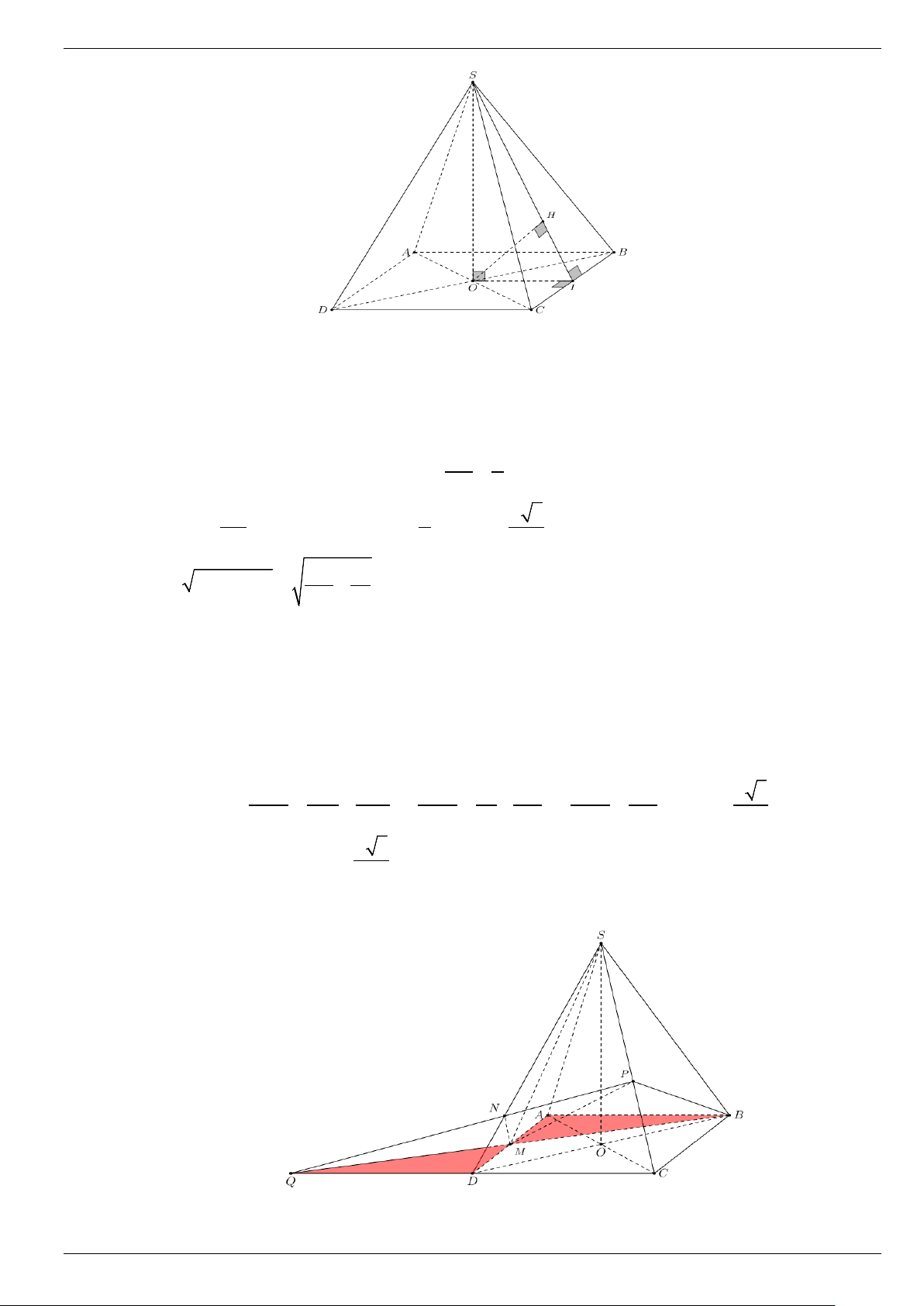
Cho hình chóp tứ giác đều S.ABCD biết AB  a , góc giữa hai mặt phẳng SBC và  ABCD bằng 60°.
a) Tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC. AM 1 SP 3
b) Lấy các điểm M, P lần lượt thuộc cạnh AD, SC sao cho  ,
 . Gọi N là giao điểm của AD 2 SC 5
SD với mặt phẳng BMP . Tính thể tích của khối đa diện SABMNP. Câu 4. (4,0 điểm) Cho tập S  1;2;3; ;  201  6 .
a) Hỏi có bao nhiêu tập con gồm 3 phần tử khác nhau chọn từ tập S, sao cho 3 số được chọn là độ dài 3
cạnh của một tam giác mà cạnh lớn nhất độ dài là 1000.
b) Chọn ngẫu nhiên 3 số khác nhau từ tập S. Tính xác suất sao cho 3 số được chọn là độ dài 3 cạnh của
một tam giác mà cạnh lớn nhất độ dài là số chẵn. Câu 5. (2,0 điểm) 1 1 2
a) Cho x, y  0 và thỏa mãn xy  1. Chứng minh rằng   . 1 x 1 y 1 xy
b) Cho a, b, c là các số thực tùy ý thỏa mãn điều kiện a  b  c  0 . Tìm giá trị nhỏ nhất của biểu thức 1  b c  3a M      .
2  a  b c  b  a  c
-------------------- HẾT -------------------- https://toanmath.com/
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . .
Chữ kí của giám thị 1: . . . . . . . . . . . . . . . . . . . . . . . Chữ kí của giám thị 2: . . . . . . . . . . . . . . . . . . . . . . .
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
ĐỀ THI HỌC SINH GIỎI - SỞ LÀO CAI
NĂM HỌC 2020 – 2021 Môn: Toán 12
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
LINK NHÓM: ht ps://www.facebook.com/groups/1916660125164699 Câu 1. (5,0 điểm)
a) Cho hàm số y = f (x) liên tục trên  , biết f ′ x = −(x + )(x − )2 ( ) 2 4 , x
∀ ∈  . Xét tính đơn
điệu của hàm số y = f ( 2
x − 3x).
b) Cho hàm số y = f x = (x + )(x − )2 ( ) 2 1 , x
∀ ∈  . Tìm tất cả các giá trị của tham số m để đồ thị hàm số 2
y = g(x) = f (x) − 2 f (x) − m có 9 điểm cực trị . Câu 2. (4,0 điểm) x x
a) Giải bất phương trình (2+ 3) − 2.(2− 3) >1.
b) Tìm cất cả các giá trị của tham số m để phương trình log (2x + m) 2
− 2log x = x − 4x − 2m −1 2 2
có hai nghiệm thực phân biệt. Câu 3. (5,0 điểm)
Cho hình chóp tứ giác đều S.ABCD biết AB = a , góc giữa hai mặt phẳng (SBC) và mặt phẳng ( ABCD) bằng 60°.
a) Tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC .
b) Lấy các điểm M , P lần lượt thuộc các cạnh AD , SC sao cho AM 1 = , SP 3 = . Gọi N là AD 2 SC 5
giao điểm của SD và mặt phẳng (BMP) . Tính thể tích của khối đa diện S.ABMNP . Câu 4. (4,0 điểm)
Cho tập S = {1;2;3;...;2016}.
a) Hỏi có bao nhiêu tập con gồm 3 phần tử khác nhau chọn từ tập S sao cho 3 số được chọn là độ
dài ba cạnh của một tam giác mà cạnh lớn nhất có độ dài là 1000.
b) Chọn ngẫu nhiên 3 số khác nhau từ tập S . Tính xác suất sao cho 3 số được chọn là độ dài ba
cạnh của một tam giác mà cạnh lớn nhất có độ dài là số chẵn. Câu 5. (2,0 điểm)
a) Cho x, y > 0 và thỏa mãn xy ≥1. Chứng minh rằng 1 1 2 + ≥ .
1+ x 1+ y 1+ xy
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
b) Cho a,b,c là các số thực tùy ý thỏa mãn điều kiện a ≥ b ≥ c > 0 . Tìm giá trị nhỏ nhất của biểu thức 1  b c  3a M = + + . 2  a b c b  + +  a + c
------------------------HẾT------------------------ Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 HƯỚNG DẪN GIẢI Câu 1. (5,0 điểm)
a) Cho hàm số y = f (x) liên tục trên  , biết f ′ x = −(x + )(x − )2 ( ) 2 4 , x
∀ ∈  . Xét tính đơn
điệu của hàm số y = f ( 2
x − 3x). Lời giải x = 2 −
 f (′x) = 0 ⇔  x = 4 (nghi m Ö kÐp)  Đặt hàm số 2
g x = f x − x → g′ x = x − f ′( 2 ( ) ( 3 ) ( ) (2 3). x − 3x)  3 x =  2 2x − 3 = 0 
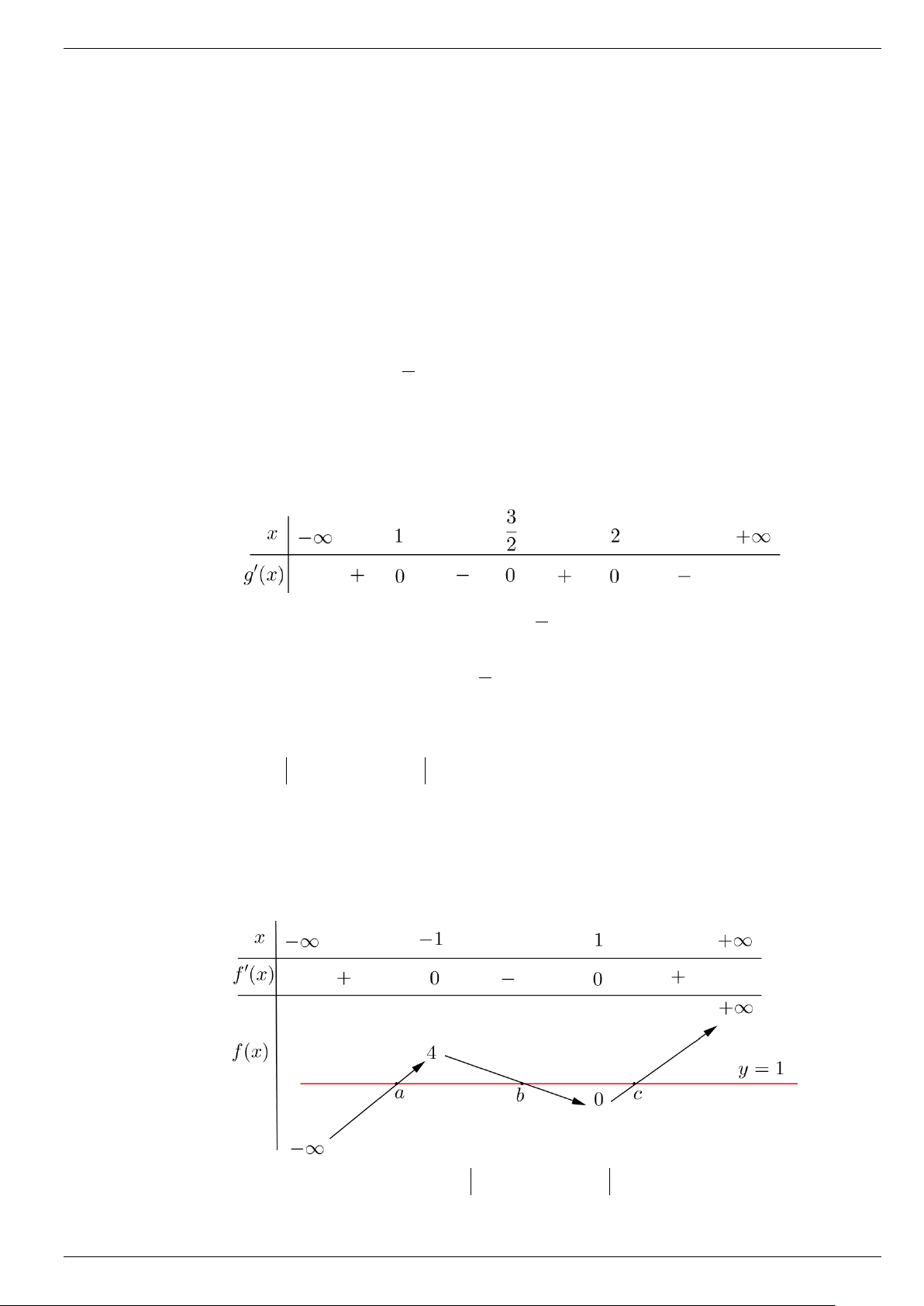
g (′x) = 0 ⇔  ⇔ x =1 2 x − 3x = 2 − x = 2    Bảng xét dấu:  
 Vậy : Hàm số đồng biến trên khoảng ( ∞ − ) 3 ;1 và ;  2 . 2   
Hàm số nghịch biến trên khoảng  3 1;    và (2;+∞) .  2 
b) Cho hàm số y = f x = (x + )(x − )2 ( ) 2 1 , x
∀ ∈  . Tìm tất cả các giá trị của tham số m để đồ thị hàm số 2
y = g(x) = f (x) − 2 f (x) − m có 9 điểm cực trị . Lời giải
 f ′ x = ( x − )2 ( ) 1 + 2(x − )
1 (x + 2) = (x − ) 1 (3x + 3) x = 1 − ⇒ y = 4
f (′x) = 0 ⇔  x =1 ⇒ y =  0
 Số điểm cực trị của hàm số 2
y = g(x) = f (x) − 2 f (x) − m bằng số điểm cực trị của hàm số 2
h(x) = f (x) − 2 f (x) − m cộng với số giao điểm ( khác điểm cực trị ) của đồ thị hàm số
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 2
h(x) = f (x) − 2 f (x) − m à v y = 0 .
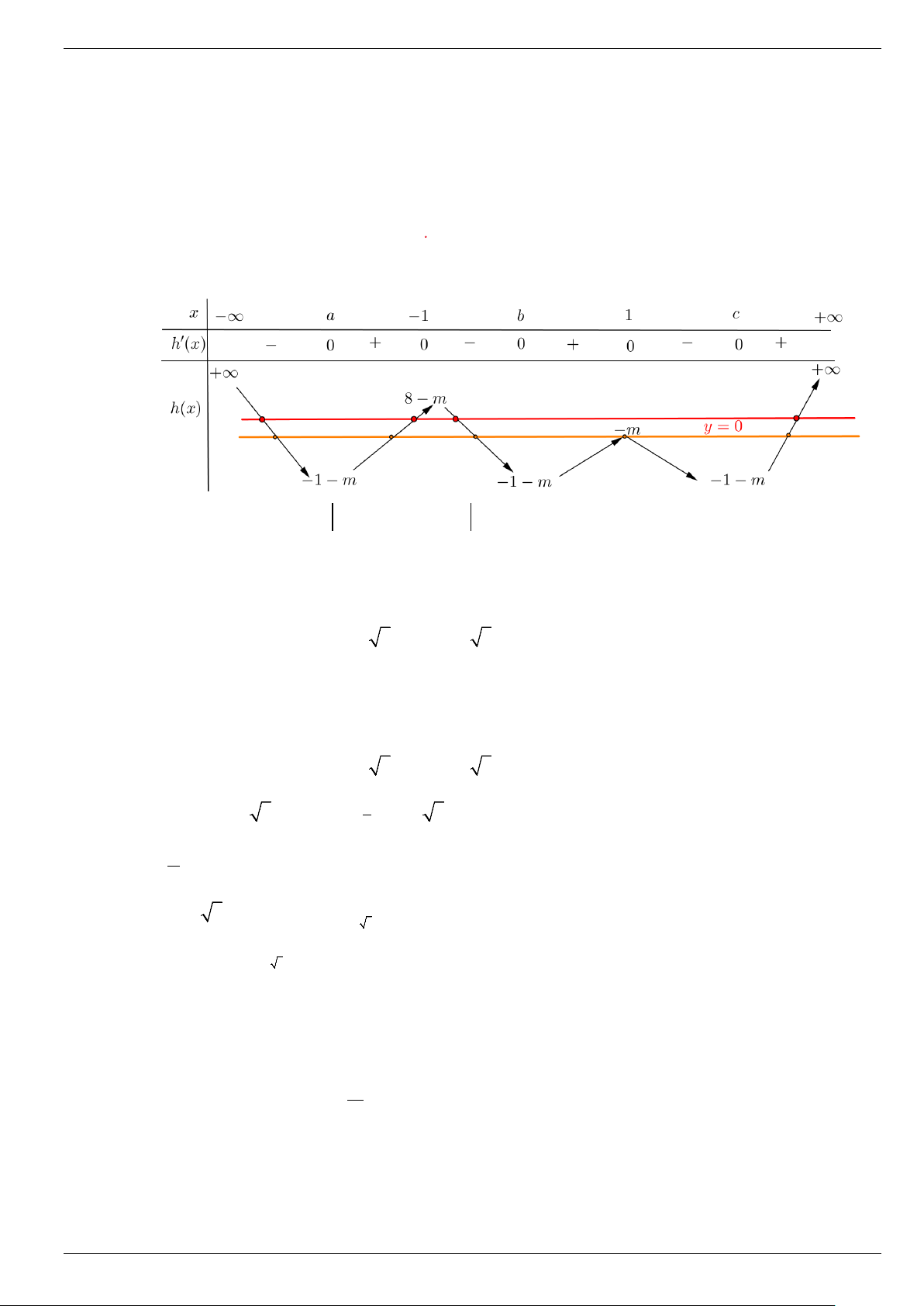
h (′x) = 2 f (′x). f (x) − 2 f (′x) = 2 f (′x).( f (x) − ) 1 x = 1 −  x = 1  f '(x) = 0 h'(x) 0  = ⇒
⇒ x = a (a < −  ) 1  f (x) 1  = x = b ( 1 − < b < ) 1 
x = c (c >  )1  Để hàm số 2
y = g(x) = f (x) − 2 f (x) − m có 9 điểm cực trị thì điều kiện :
−m ≤ 0 < 8 − m ⇔ 0 ≤ m < 8 . Câu 2. (4,0 điểm) a) x x
Giải bất phương trình (2+ 3) − 2.(2− 3) >1.
b) Tìm tất cả các giá trị của tham số m để phương trình log (2x + m) 2
− 2log x = x − 4x − 2m −1 2 2
có hai nghiệm thực phân biệt. Lời giải a) x x
Giải bất phương trình (2+ 3) − 2.(2− 3) >1. x 1 x
 Đặt t = (2 + 3) (t > 0) ⇒ = (2 − 3) , bất phương trình trở thành: t 2 2 2
t − >1 ⇔ t − 2 > t ⇔ t − t − 2 > 0 ⇔ t > 2 vì t > 0 t ⇒ ( x
2 + 3) > 2 ⇔ x > log 2 2+ 3  Vậy S = (log 2;+∞ . 2+ 3 )
b) Tìm tất cả các giá trị của tham số m để phương trình  log (2x + m) 2
− 2log x = x − 4x − 2m −1 có hai nghiệm thực phân biệt. 2 2 x > 0
Điều kiện xác định:  m x > −  2
 Ta có: log (2x + m) 2
− 2log x = x − 4x − 2m −1 2 2 Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 ⇔ log (2x + m) 2 2
+1− log x = x − 4x − 2m 2 2 ⇔ log (2x + m) 2 2
+ log 2 − log x = x − 4x − 2m 2 2 2
⇔ log (4x + 2m) 2 2
− log x = x − 4x − 2m 2 2
⇔ log (4x + 2m) 2 2
+ 4x + 2m = x + log x 2 2
 Xét hàm số f (t) = log t + t với t > 0 . 2 ⇒ f ′(t) 1 =
+1 > 0 với t > 0 . t ln 2
⇒ f (t) đồng biến trên (0;+∞).
⇒ f ( x + m) = f ( 2 x ) 2 4 2
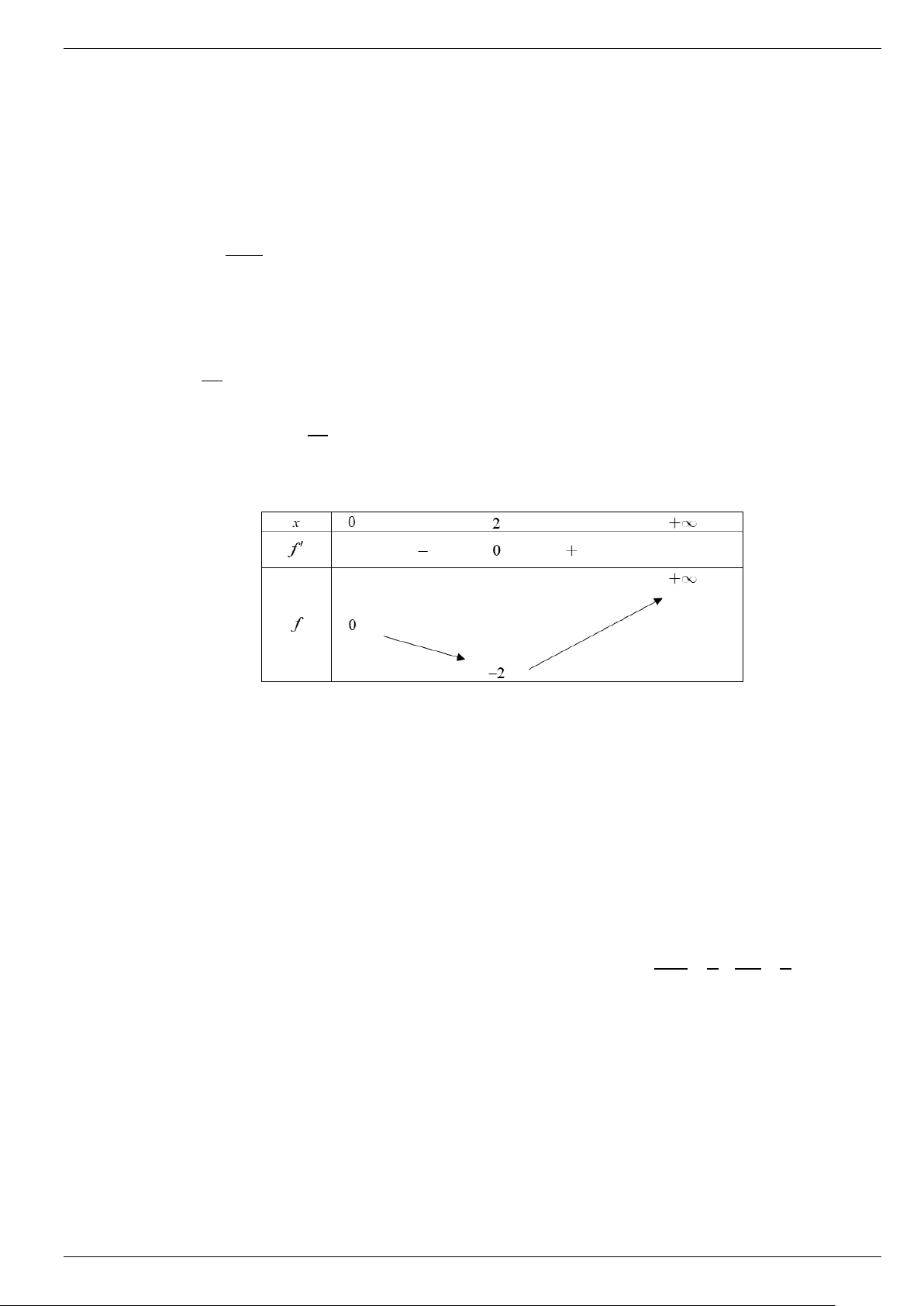
⇔ 4x + 2m = x 2 x ⇔ m = − 2x ( ) 1 2 2 x
 Xét hàm số f ( x) =
− 2x với x > 0 ⇒ f ′(x) = x − 2 . 2
⇒ f ′(x) = 0 ⇔ x − 2 = 0 ⇔ x = 2 .
 Để phương trình log (2x + m) 2
− 2log x = x − 4x − 2m −1 có hai nghiệm thực phân biệt 2 2 ⇔ Phương trình ( )
1 có hai nghiệm thực phân biệt ⇔ m∈( 2; − 0). Câu 3. (5,0 điểm)
Cho hình chóp tứ giác đều S.ABCD biết AB = a , góc giữa hai mặt phẳng (SBC) và mặt phẳng ( ABCD) bằng 60°.
a) Tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC .
b) Lấy các điểm M , P lần lượt thuộc các cạnh AD , SC sao cho AM 1 = , SP 3 = . Gọi N là AD 2 SC 5
giao điểm của SD và mặt phẳng (BMP) . Tính thể tích của khối đa diện S.ABMNP . Lời giải
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
a) Gọi I là trung điểm BC . OI  ⊥ BC  Khi đó ta có 
⇒ BC ⊥(SOI )⇒ BC ⊥ SI . SO ⊥ BC
Suy ra góc giữa hai mặt phẳng (SBC) và mặt phẳng ( ABCD) là góc  SIO hay  SIO = 60°. AB a  Trong S
∆ IO vuông tại O ta có: OI = = 2 2  SO = ⇔ =  a a 3 tan SIO
SO OI.tan SIO = .tan 60° = OI 2 2 2 2 2 2 3a a
SI = SO + OI = + = a . 4 4
Do AB // CD ⇒ AB // (SCD) ⇒ d( AB, SC) = d( AB,(SCD)) = 2d(O,(SCD)) = 2d(O,(SBC)).  Trong S
∆ IO kẻ OH ⊥ SI ( )
1 với H ∈ SI .
 Do BC ⊥ (SOI ) ⇒ BC ⊥ OH (2) .
 Từ (1) và (2) suy ra OH ⊥ (SBC) . Vậy d(O,(SBC)) = OH .  Trong S
∆ IO vuông tại O ta có: 1 1 1 1 4 4 1 16 a 3 = + ⇔ = + ⇔ = ⇔ OH = . 2 2 2 2 2 2 2 2 OH OI SO OH a 3a OH 3a 4 a  Vậy ( AB SC) 3 d , = 2OH = . 2
b) Gọi Q là giao điểm của CD và BM . Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
Q ∈(MBP) ∩(SCD)  Ta có:
 ⇒ (MBP) ∩(SCD) . ∈( )∩( ) = PQ P MBP SCD 
 Gọi N là giao điểm của SD và PQ .
 Do PQ ⊂ (BMP) ⇒ SD ∩(BMP) = N .  Trong SC
∆ D có P , N , Q thẳng hàng nên theo định lý Menelaus ta có PS QC ND 3 ND ND 1 . . =1 ⇔ − .2. =1 ⇔ = − . PC QD NS 2 NS NS 3 3 1 1 a 3 a 3
 Thể tích tứ diện S.ABCD là 2 V = SO S = a = (đvtt). S ABCD . . ABCD . . . 3 3 2 6  Ta thấy A ∆ MB = D
∆ MQ (c – g – c) 2 ⇒ S = = . ∆ S a BCQ ABCD (P (ABCD)) 2 = (S (ABCD)) 2 a 3 d , d , = .SO = . 5 5 5 1 1 a 3 a 3  V P ABCD S = = . ∆ a P QBC = .d( ,( )) 3 2 . BQC . . . 3 3 5 15 (N (ABCD)) 1 = (S (ABCD)) 1 1 a 3 a 3 d , d , = .SO = . = . 4 4 4 2 8 2 1 a S = = = . ∆ S∆ AB AM MDQ MAB . . 2 4 1 a a a N ABCD S = = (đvtt). N MDQ ( ( )) 2 3 1 3 3 V = .d , . MD ∆ Q . . . 3 3 8 4 96 3 3 3
a 3 a 3 9a 3
 Thể tích khối đa diện PNBCDM là V = V −V = − = (đvtt). PNBCDM P.BQC N.DQM 15 96 160
Vậy thể tích khối đa diện S.ABMNP là 3 3 3
a 3 9a 3 53a 3 V = V −V = − = (đvtt). S.ABMNP S.ABCD PNBCDM 6 160 480 Câu 4. (4,0 điểm)
Cho tập S = {1;2;3;...;2016}.
a) Hỏi có bao nhiêu tập con gồm 3 phần tử khác nhau chọn từ tập S sao cho 3 số được chọn là độ
dài ba cạnh của một tam giác mà cạnh lớn nhất có độ dài là 1000.
b) Chọn ngẫu nhiên 3 số khác nhau từ tập S . Tính xác suất sao cho 3 số được chọn là độ dài ba
cạnh của một tam giác mà cạnh lớn nhất có độ dài là số chẵn. Lời giải Lời giải tổng quát
 Với mỗi k . Xét tập S =
k − . Bài toán trên tương đương với bài toán: “Có bao nhiêu k {1;2;...; 1}
cách chọn 2 phần tử phân biệt của S sao cho tổng của chúng lớn hơn k ”. k
Giả sử hai phần tử được chọn là 1≤ a < b ≤ k −1 .
Đặt s = a + b . Suy ra k +1≤ s ≤ 2k − 3 . Vậy với mỗi s cố định thì a hoàn toàn xác định khi biết
b . Từ điều kiện của a,b ta có s s
 Nếu s chẵn thì +1 ≤ b ≤ k −1. Suy ra có k −1− cách. 2 2
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 s + s  Nếu s lẻ thì
1 ≤ b ≤ k −1. Suy ra có 1 k + − cách 2 2
Vậy nếu k chẵn thì có  k + 2   k + 4   2k − 2 P k   k    k  = − + − + + − k 2 2 2         k + 2   k + 4   2k − 2 k 1   k 1    k 1  + − − + − − + + − −  2 2 2         +   +   −  − Rút gọn được k 2 k 4 2k 4 k 4 P = k − +   k − ++   k − + − k 2  1  2   2   2  2 = (k − ) k − 4
 k − 2 k − 4  k − 2
2 + (k − 4) ++ 4 +1− = 2 + ++   2 +1 − 2  2 2   2
 k − 2  k − 2  k − 2 1 2 = +1 − = (k −    2)  2  2  2 4
a) Với k =1000 ta có 2 499 tập con của S 1008 1008
b) Với k = 2i chẵn và thuộc S ta có 1 2 2 1007.1008.(2.1007 +1)
B = ∑4(i −1) = ∑(i −1) = cách 4 i 1= i 1 = 6 chọn Vậy xác suất là B 1 = 3 C 4 2016
Trường hợp k lẻ  k + 3   k + 5   2k − 2 P k   k    k  = − + − + + − k 2 2 2         k +1  k + 3   2k − 4 k 1   k 1    k 1  + − − + − − + + − −  2 2 2        Rút gọn được  k + 3   k + 5   2k − 2 P = k − +   k − ++   k  − k 2  2 2 2       
= [ k − + k − ++ ] 1 ( 3) ( 5)
1 = (k −1)(k − 3) 4
Vậy số tam giác mà cạnh lớn nhất có độ dài là số lẻ k = 2i +1 là: 1007 2
1007.1008.(2.1007 +1) 1007.1008
C = ∑(i −i) = − i 1 = 6 2
Vậy số cách chọn ba số lập thành ba cạnh của tam giác là 1007.1008.(2.1007 1) 1007.1008 C + = − 3 2
Từ đây có thể tổng quát thay 2016 bằng n bất kì. Câu 5. (2,0 điểm)
a) Cho x, y > 0 và thỏa mãn xy ≥1. Chứng minh rằng 1 1 2 + ≥ .
1+ x 1+ y 1+ xy Lời giải
 Bất đẳng thức cần chứng minh tương đương với Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021     xy − x xy − y 1 1 1 1  −  +  −  ≥ 0 ⇔ + ≥ 0  1 x  1+ xy  1 y   1+ xy  + + 
(x + )1(1+ xy) (y + )1(1+ xy)
x − y  y x  x − y
y − x + x y − y x ⇔  −  ≥ 0 ⇔ . ≥ 1+ xy  y x  + + 1+   xy ( + x)( + y) 0 1 1 1 1
( x − y)( xy − ) ( x − y)2 1 ( xy x y − − )1 ⇔ . ≥ ⇔ ≥ 1+ xy ( + x)( + y) 0 (1+ xy) 0 1 1 (1+ x)(1+ y) (luôn đúng với x
∀ , y > 0 và xy ≥1).
 Dấu “=” xảy ra khi và chỉ khi x = y hoặc xy =1.
b) Cho a,b,c là các số thực tùy ý thỏa mãn điều kiện a ≥ b ≥ c > 0 . Tìm giá trị nhỏ nhất của biểu thức 1  b c  3a M = + + . 2  a b c b  + +  a + c Lời giải  b c  a  Ta có : 1 3 1 1 6 M = + + ⇔   2M = + + .
2  a + b c + b  a + c a +1 1 b + 1 c + b c a  a u =  Đặt  b 
, vì a ≥ b ≥ c > 0 nên u ≥ v ≥1. Suy ra a uv = . b v = c  c
Thay vào biểu thức trên ta có: 1 1 6 2M = + + . u +1 v +1 1 1+ uv u  +1 ≤ uv +1
Do u ≥ v ≥1 nên  , suy ra 1 1 2 + ≥ .
v +1 ≤ uv +1
u +1 v +1 1+ uv uv + uv  Khi đó 2 6 1 3 2 2M ≥ + ⇔ M ≥ ⇔ M ≥ 3− . 1+ uv 1+ uv 1+ uv 1+ uv Vì 2
uv ≥1 ⇔ 1+ uv ≥ 2 ⇔
≤ 1, suy ra M ≥ 2 . 1+ uv
Vậy giá trị nhỏ nhất của biểu thức M bằng 2 đạt được khi u = v =1, tức là a = b = c .
------------------------HẾT------------------------
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
Document Outline

• de-thi-hoc-sinh-gioi-tinh-toan-thpt-nam-2020-2021-so-gddt-lao-cai
• TOÁN-VDC&-HSG5-HSG-TOÁN-12-SỞ-LÀO-CAI-2020-2021-HOÀN-THIỆN