Đề thi học sinh giỏi Toán 11 năm 2021 – 2022 cụm trường THPT – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề thi chọn học sinh giỏi cấp cụm môn Toán 11 năm học 2021 – 2022 cụm trường THPT trực thuộc sở Giáo dục và Đào tạo Hà Nội.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
CỤM TRƯỜNG THPT
ĐỀ CHÍNH THỨC
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
NĂM HỌC 2021 - 2022
Môn thi: TOÁN
Thơ
i gian la
m ba
i: 150 phu
t
Bài I (5,0 điểm)
1) Giải các phương trình sau :
a)
sin 2 4cos sin 2 0;x x x
b)
sin cot 2 cos3 .x x x
2) Giải hệ phương trình
5 2 2 5
.
21
x y x y
x y x y
Bài II (3,0 điểm)
1) Tìm số tự nhiên
x
thỏa mãn
.
2) Tìm hệ số của
5
x
trong khai triển



5
3
2
2
.x
x
3) Hỏi có bao nhiêu số tự nhiên có 5 chữ số trong đó có ít nhất một chữ số 1.
Bài III (4,0 điểm) Cho dãy số
n
u
thoả mãn
11
1, 3 2 , 1
nn
u u u n
.
1) Chứng minh dãy số
1
n
u
là một cấp số nhân, tính
50
.u
2) Chứng minh
1 2 100
1 1 1 3
...
1 1 1 4u u u
.
3) Tìm công thức tổng quát của dãy số
11
1; , 1
23
n
n
n
v
v v n
v
.
Bài IV (2,0 điểm) Tính giới hạn
3
1
2 1 3 2
lim .
1
x
xx
x
Bài V (6,0 điểm) Cho hình hộp
. ' ' ' 'ABCD A B C D
có các góc
0
' ' 60BAD DAA BAA
và tất
cả các cạnh bằng
.a
1) Chứng minh
' ' 'BA B C
và tính độ dài cạnh
'AC
theo
.a
2) Lấy các điểm
,,M N P
thỏa mãn
0,MA MB
2 0,NB NC
2 ' 0.PC PC
Dựng thiết diện của hình hộp
. ' ' ' 'ABCD A B C D
cắt bởi mặt phẳng
( ).MNP
3) Mặt phẳng
()MNP
cắt đường thẳng
'DB
tại
.I
Tính tỷ số
'
.
DI
BI
- - - - - - - - - - Hết - - - - - - - - -
Họ và tên thí sinh:.................................................... Số báo danh:..................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
CỤM TRƯỜNG THPT
HƯỚNG DẪN CHẤM
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
NĂM HỌC 2021 - 2022
Môn thi: TOÁN
Bài
Câu
Nội dung
Điểm
1
(5,0đ)
1a
sin 2 4cos sin 2 0 (sin 2)(2cos 1) 0x x x x x
sin 2
1
cos
2
x
x
1,0
+)
sin 2( )xl
+)
1
cos 2 .
23
x x k
1,0
1b
ĐK:
sin 2 0 .
2
k
xx
0,25
sin cot 2 cos3 sin .cos2 cos3 .sin2x x x x x x x
11
(sin 3 sin ) (sin 5 sin )
22
x x x x
1,0




5 3 2
sin 3 sin 5
5 3 2
84
xk
x x k
xx
k
x x k
x
0,5
Kết hợp điều kiện
2
k
x
suy ra


84
k
x
.
Vậy nghiệm của phương trình là


84
k
x
.
0,5
2
Đặt




2 2 2
2 2 2
5 2 5 2 2
( 0, 0)
2 5 2
2
x y a x y a x a b
ab
x y b y b a
x y b
0,25
Khi đó hệ phương trình trở thành





2 2 2 2 2 2
55
2 (5 2 ) 1 3(5 ) 7 1 0
a b a b
b a b b a b b b

2
5
4 29 74 0
ab
bb


2, 3
37
()
4
ba
bl
0,5
Với





5 2 9 1
2, 3
2 4 2
x y x
ba
x y y
Vậy hệ có nghiệm là
1;2
0,25
2
(3,0đ)
1
Điều kiện:
, 3.xx
0,25
ta có

2 2 3
2
1 6 1 6 ( 1)( 2)
10 .2 (2 1) ( 1) 10
2 2 3!
x x x
x x x
A A C x x x x
xx
0,25
(2 1) ( 1) ( 1)( 2) 10x x x x x x
3 12 4.xx
0,25
Kết hợp điều kiện suy ra
3x
hoặc
4x
0,25
2



55
55
5
3 3 5 10
55
22
00
22
2
k
k
k k k k
kk
x C x C x
xx
0,5
Hệ số của
5
x
trong khai triển thỏa mãn:
5 10 5 3.kk
Vậy hệ số của
5
x
trong khai triển là:

2
3
5
2 40C
0,5
3
Gọi số cần tìm là
abcde
Số các số tự nhiên có 5 chữ số là:
4
9.10
0,5
Số các số tự nhiên có 5 chữ số trong đó không có chữ số 1 là:
4
8.9
0,25
Số các số tự nhiên có 5 chữ số trong đó có ít nhất 1 chữ số 1 là:
44
9.10 8.9 37512
số
0,25
3
(4,0đ)
1
Ta có:
1
1 3( 1) , 1
nn
u u n
Suy ra
1
n
u
là cấp số nhân với công bội 2
0,5
Ta có:
49 49
50 1
1 3 . 1 2.3uu
Suy ra

49
50
2.3 1u
0,5
2
Ta có




1
1
n
u
là cấp số nhân với công bội bằng
1
3
.
0,5



100
100
99
1 2 100 1
1
1
3
1 1 1 1 1 3 1 3
...
1 1 1 1 1 2 4
2. 3
1
3
u u u u
0,5
3
1
2 3 3
1
2 , 1
n
n n n
v
n
v v v
0,25
Đặt
11
1
1; 2 3 , 1
n n n
n
w w w w n
v
0,25
Theo câu a suy ra

1
2.3 1
n
n
w
0,25
Vậy
1
1
,1
2.3 1
n
n
vn
0,25
4
(2,0đ)
1







33
11
2 1 3 2 2 1 1 3 2 1
lim lim .
1 1 1
xx
x x x x
x x x
0,5











1 1 1
2 1 1
2 1 1 2
lim lim lim 1.
1
2 1 1
1 2 1 1
x x x
x
x
x
x
xx
0,5


















3
11
2
3
3
1
2
3
3
3 2 1
3 2 1
lim lim
1
1 3 2 3 2 1
3
lim 1.
3 2 3 2 1
xx
x
x
x
x
x x x
xx
0,5
3
1
2 1 3 2
lim 0.
1
x
xx
x
5
(6,0đ)
1
Ta có :
''BA AA AB
''B C AD
Suy ra
22
'. ' ' ' 0
22
aa
BA B C AA AB AD
Suy ra
' ' 'BA B C
0,25
0,25
0,5
''AC AA AB AD
0,25
2
2
2
2 2 2 2
' ' '
' 2 '. 2 ' 2 6
AC AC AA AB AD
AA AB AD AA AB AA AD ABAD a
0,5
'6AC a
0,5
2
Gọi giao của MN với CD và AD là E và F
0,5
Gọi giao của MN với CD và AD là E và F
0,5
Gọi giao của EP với C’D’ và DD’ là Q và G
0,5
Gọi giao của FG với AA’ và A’D’ là S và R
Suy ra thiết diện là lục giác MNPQRS
0,5
3
Gọi H,K là giao của MN với BD và QR với
B’D’
0,25
Chứng minh tứ giác BKD’H là hình bình hành
0,5
Suy ra I là trung điểm của BD’
Vậy
'
1.
DI
BI
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11 CỤM TRƯỜNG THPT
NĂM HỌC 2021 - 2022 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
Bài I (5,0 điểm)
1) Giải các phương trình sau :
a) sin 2x  4 cos x  sin x  2  0;
b) sin x cot 2x  cos 3x.
 5x  2y  2x y  5
2) Giải hệ phương trình  .
 2x y x y   1
Bài II (3,0 điểm) 1 6
1) Tìm số tự nhiên x thỏa mãn 2 A  2 A  3 C  10 . 2x 2 x x x  2 5 2) Tìm hệ số của 5
x trong khai triển  3 x  . 2   x
3) Hỏi có bao nhiêu số tự nhiên có 5 chữ số trong đó có ít nhất một chữ số 1.
Bài III (4,0 điểm) Cho dãy số u thoả mãn u  1, u
 3u  2 , n  1. n  1 n 1 n
1) Chứng minh dãy số u  1 là một cấp số nhân, tính u . n  50 1 1 1 3 2) Chứng minh   ...   . u  1 u  1 u  1 4 1 2 100 v
3) Tìm công thức tổng quát của dãy số v  1;vn , n  1 . 1 n 1 2v  3 n
 2x 1 3 3x 2
Bài IV (2,0 điểm) Tính giới hạn lim . x 1 x  1
Bài V (6,0 điểm) Cho hình hộp ABC .
D A ' B 'C ' D ' có các góc BA D DA A BA A  0 ' ' 60 và tất
cả các cạnh bằng a.
1) Chứng minh BA '  B 'C ' và tính độ dài cạnh AC ' theo a.
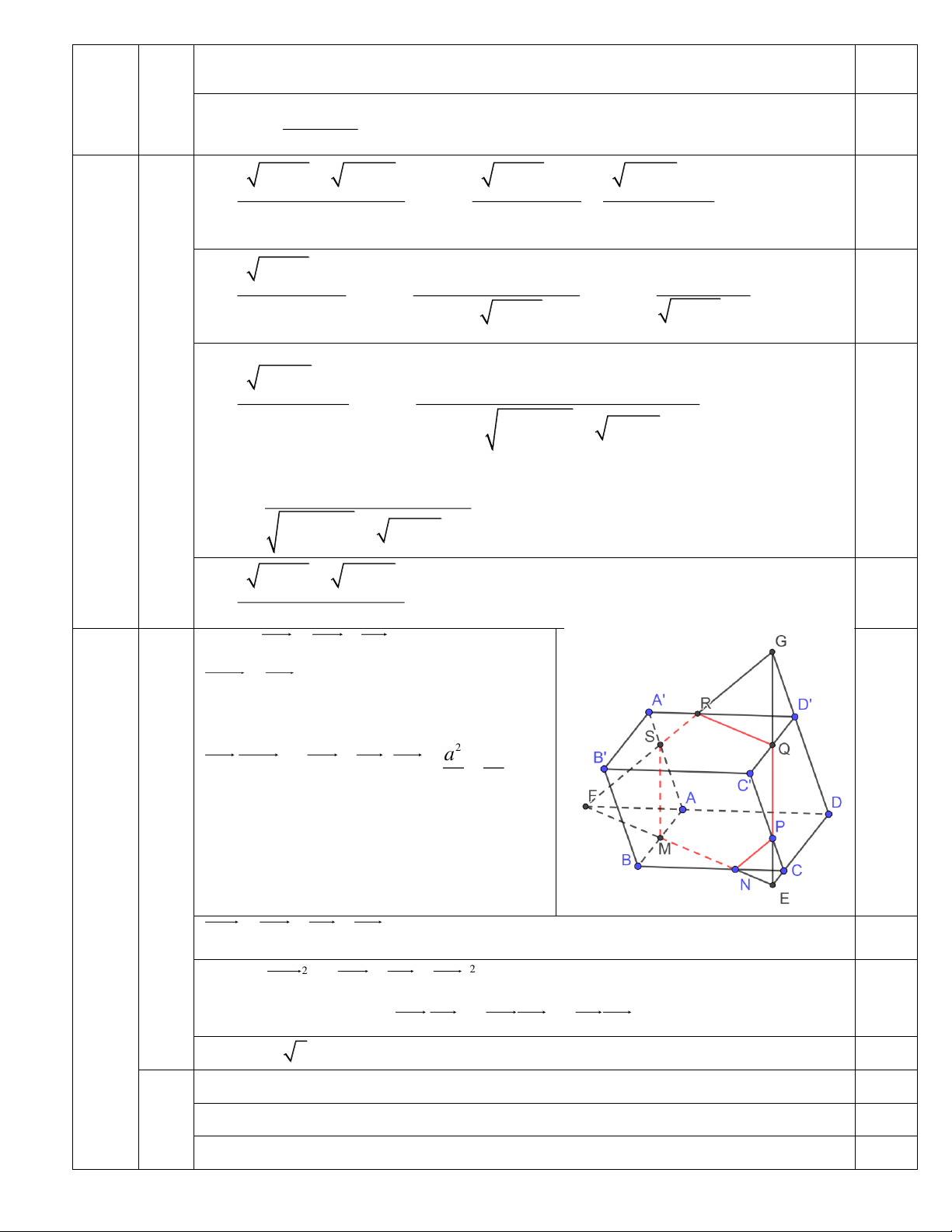
2) Lấy các điểm M , N , P thỏa mãn MA MB  0, NB  2NC  0, 2PC PC '  0.
Dựng thiết diện của hình hộp ABC .
D A ' B 'C ' D ' cắt bởi mặt phẳng (MNP ). D ' I
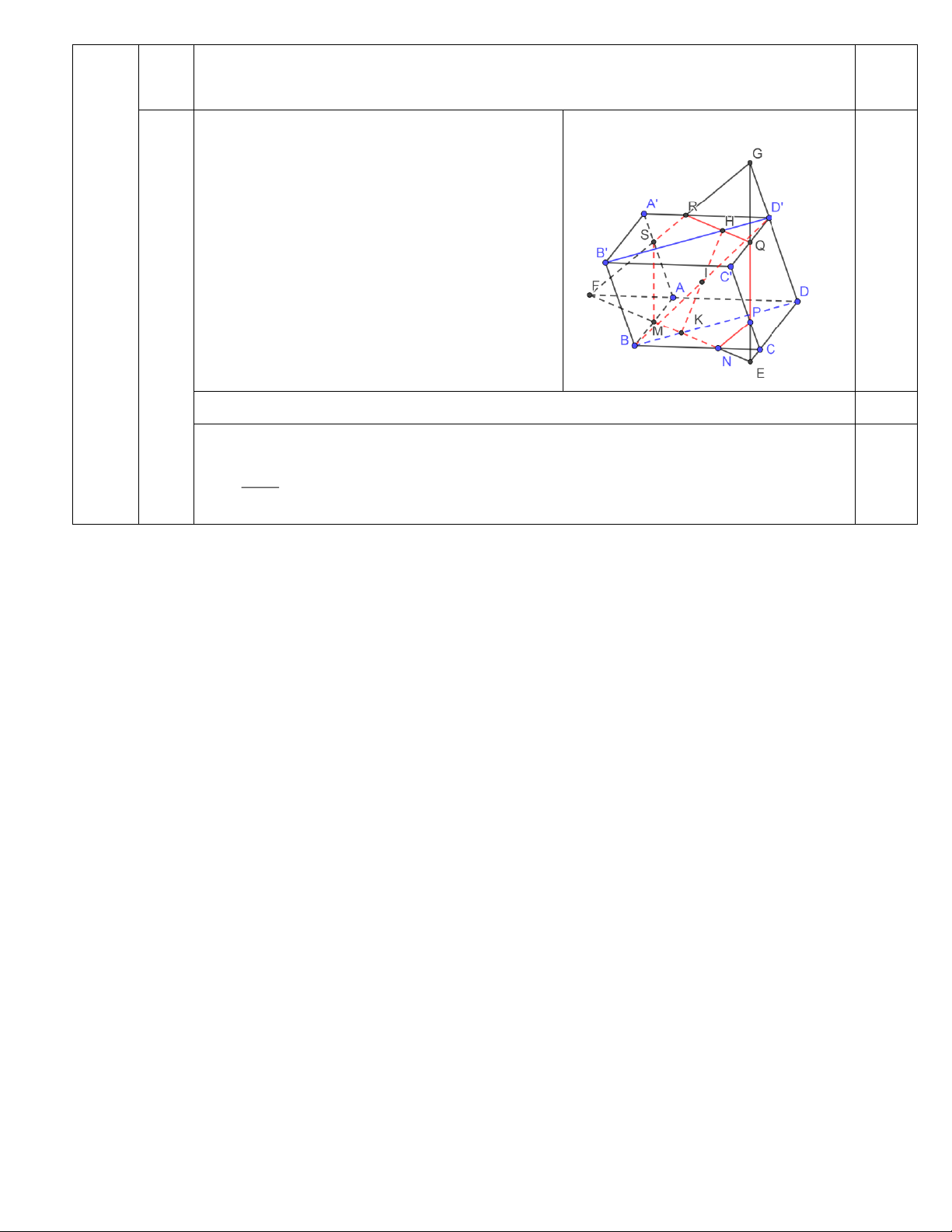
3) Mặt phẳng (MNP ) cắt đường thẳng D ' B tại I . Tính tỷ số . B I
- - - - - - - - - - Hết - - - - - - - - -
Họ và tên thí sinh:.................................................... Số báo danh:..................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11 CỤM TRƯỜNG THPT NĂM HỌC 2021 - 2022 Môn thi: TOÁN HƯỚNG DẪN CHẤM Bài Câu Nội dung Điểm 1 1a sin x  2 (5,0đ) 
sin 2x  4 cos x  sin x  2  0  (sin x  2)(2 cos x  1)  0   cos x  1 1,0  2
+) sin x  2(l) 1  +) cos x
x    k  2 . 1,0 2 3 1b k
ĐK: sin 2x  0  x  . 0,25 2
sin x cot 2x  cos 3x  sin x. cos 2x  cos 3x.sin2x  1 x x  1 (sin 3 sin )
(sin 5x  sin x ) 1,0 2 2 x k
5x  3x k  2 
 sin 3x  sin 5x     k 0,5
5x    3x k  2   x     8 4 k  k
Kết hợp điều kiện x  suy ra x   . 2 8 4  0,5 k
Vậy nghiệm của phương trình là x   . 8 4 2 
 5x  2y a
5x  2y  2 a x  2 a  2 2b Đặt 
(a  0,b  0)    2    
2x y b y  2 5b   2    2 2 a x y b 0,25
Khi đó hệ phương trình trở thành
a b  5
a  5 b   2 2 2 2 
b a  2b  (5b  2a )  1 3(5  2 ) b  2
7b b  1    0 0,5  b  2,a  a  5 b 3     2 37
4b  29b  74     0 b    (l)  4
5x  2y  9 x  1
Với  b  2,a  3     2x y  4 y    2
Vậy hệ có nghiệm là  0,25 1; 2 2 1
Điều kiện: x  , x  3. 0,25 (3,0đ) ta có 1 6 1 6 x(x 1)(x 2) 2 2 3   A
A C  10  .2x(2x  1)  x(x  1)   10 0,25 2 2 x x x x 2 x 3 !
x(2x  1)  x(x  1)  (x  1)(x  2)  10  0,25
3x  12  x  4.
Kết hợp điều kiện suy ra x  3 hoặc x  4 0,25 2 5 5  k 2  5  k k 2  5 5 k  3 x k C x C 2 k x 2    3   2 
     5 10 5 5 x 0,5 k 0 x k      0 Hệ số của 5
x trong khai triển thỏa mãn: 5k  10  5  k  3. 2 0,5 Vậy hệ số của 5
x trong khai triển là: 3 C 2 40 5     3
Gọi số cần tìm là abcde 0,5
Số các số tự nhiên có 5 chữ số là: 4 9.10
Số các số tự nhiên có 5 chữ số trong đó không có chữ số 1 là: 4 8.9 0,25
Số các số tự nhiên có 5 chữ số trong đó có ít nhất 1 chữ số 1 là: 0,25 4 4 9.10  8.9  37512 số 3 1 Ta có: u
 1  3(u  1) , n  1 (4,0đ) n  1 n
Suy ra u  1 là cấp số nhân với công bội 2 0,5 n  Ta có: u   1  49 3 . u  1  49 2.3 50 1 49 Suy ra u  2.3  1 50 0,5 2  1  Ta có   
 là cấp số nhân với công bội bằng 1 . u   1 3 n  0,5  1 100    1 1 1 1 1  3  100 1 3  0,5      1  3 ... u  1 u  1 u  1 u  99 1 1 2 2.3 4 1 2 100 1  1 3 3 2v  3 3 1  n  2  , n  1 v v v 0,25 n 1 n n 1 Đặt w   w  1;w
 2  3w , n  1 0,25 n 1 n 1 n vn n
Theo câu a suy ra w  1 2.3  1 n 0,25 1 Vậy v  , n  1 0,25 n n 1 2.3  1 4 1  3 2x 1 3x 2   3
  2x 1 1  3x 2 1         (2,0đ)  lim  lim  . 0,5 x 1 x 1   x  1 x  1 x   1     2x 1      1  2x  1  1   2  lim  lim  lim    1. 0,5 x 1 x 1  x  1  x   x 1 1 2x 1 1 2x 1 1             3 3x 2 1     3x  2   1  lim  lim x 1 x x  1 1  2
 x  1  3 3x  2 3  
 3x  2  1      0,5    3   lim    1.
x 1  3x  22  3 3 3x  2  1   
 2x 1 3 3x 2 lim  0. x 1 x  1 5 1
Ta có : BA'  AA'  AB (6,0đ)
B 'C '  AD Suy ra 0,25
B C   AA AB 2 2 a a BA'. ' ' ' AD    0 0,25 2 2
Suy ra BA '  B 'C ' 0,5
AC '  AA'  AB AD 0,25 2 2
AC '  AC '   AA'  AB AD2 2 2 2 2
AA'  AB AD  2AA'.AB  2AA'AD  2ABAD  6a 0,5
AC '  6a 0,5 2
Gọi giao của MN với CD và AD là E và F 0,5
Gọi giao của MN với CD và AD là E và F 0,5
Gọi giao của EP với C’D’ và DD’ là Q và G 0,5
Gọi giao của FG với AA’ và A’D’ là S và R
Suy ra thiết diện là lục giác MNPQRS 0,5 3
Gọi H,K là giao của MN với BD và QR với B’D’ 0,25
Chứng minh tứ giác BKD’H là hình bình hành 0,5
Suy ra I là trung điểm của BD’ D ' I Vậy  1. BI