Đề thi học sinh giỏi Toán 12 cấp tỉnh năm 2017 – 2018 sở GD&ĐT Lai Châu

UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018 Môn: Toán
ĐỀ THI CHÍNH THỨC
(Đề thi có 01 trang)
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 22/4/2018
Câu 1 ( 6,0 điểm)
a) Cho hàm số 4 2
y = x − mx + m −1 có đồ thị là (C .Tìm tất cả các giá trị thực của m )
tham số m đ ể đồ thị (C cắt trục hoành tại bốn điểm phân biệt. m )
b) Cho hàm số y = f (x) liên tục trên  thỏa mãn f ( 3
x + 2x − 2) = 2x −1. Tính tích 10 phân I = f ∫ (x)dx . 1
c) Tìm tất cả các giá trị thực của tham số m để phương trình x x 2 25 − 2.10 + 4x m = 0 có hai nghiệm trái dấu.
Câu 2 ( 4,0 điểm)
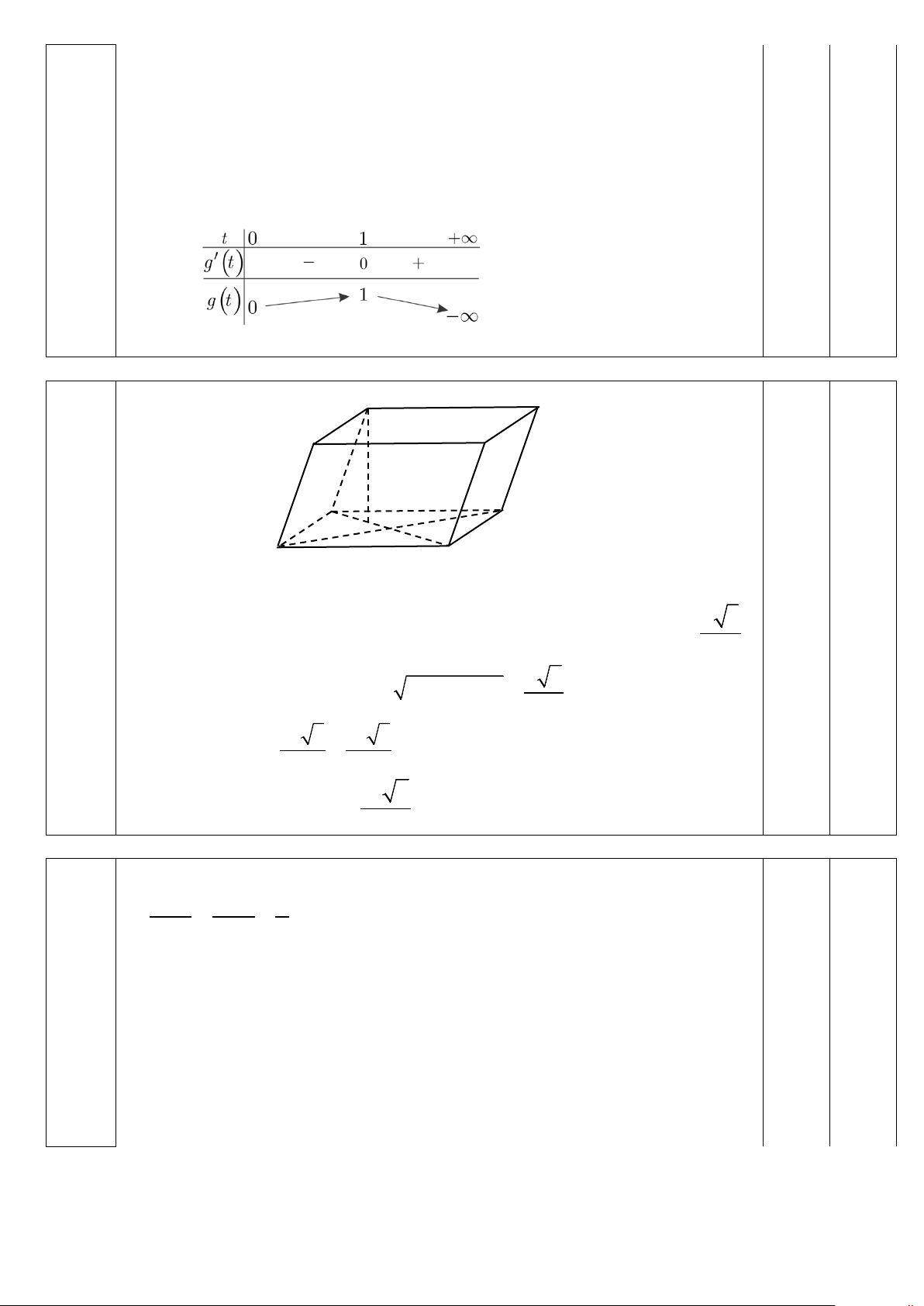
a) Cho hình lăng trụ ABC .
D A'B'C 'D' có đáy ABCD là hình thoi. Hình chiếu
vuông góc của A' lên ( ABCD) là trọng tâm của tam giác ABD . Biết AB = a ,  0
ABC =120 , AA' = a . Tính thể tích khối lăng trụ ABC .
D A'B'C 'D' theo a .
b) Trong không gian với hệ tọa độ Oxyz , cho đường thẳng x − 3 y − 3 : z d = = , mặt 1 3 2
phẳng (α) : x + y − z + 3 = 0 và điểm A(1;2;−1). Viết phương trình chính tắc của
đường thẳng ∆ đi qua điểm A , cắt đường thẳng d và song song với mặt phẳng (α) . 2 2
x 2y  x  y  63xy
Câu 3 ( 4,0 điểm) Giải hệ phương trình  3 2  4
x 2x  y  2x3  12  y
Câu 4 ( 3,0 điểm) Cho các số thực không âm a,b,c thỏa mãn a + b + c =1. Tìm giá trị lớn
nhất của biểu thức P = ab + 3ac + 5bc.
Câu 5 ( 3,0 điểm) Có 20 người xếp thành một vòng tròn. Hỏi có bao nhiêu cách chọn ra 5
người sao cho không có hai người kề nhau được chọn.
...................................Hết...............................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. Trang 01/01 UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018
ĐÁP ÁN THANG ĐIỂM Môn: Toán
HƯỚNG DẪN CHẤM
- Điểm bài thi là tổng điểm của các câu thành phần. Thang điểm toàn bài là 20 điểm,
không được làm tròn (điểm lẻ từng ý trong một câu nhỏ nhất là 0,25)
- Thí sinh làm bài bằng cách khác, lập luận chặt chẽ, logic, ra kết quả đúng vẫn cho điểm tối đa.
ĐÁP ÁN, BIỂU ĐIỂM a) Cho hàm số 4 2
y = x − mx + m −1 có đồ thị là (C .Tìm tất cả các giá trị m )
thực của tham số m để đồ thị (C cắt trục hoành tại bốn điểm phân biệt. m )
Phương trình hoành độ giao điểm của (C và trục hoành là: m ) 0.5 4 2
x − mx + m −1= 0 (1) Câu 1 t = Ý a 1 Đặt 2
t = x (t ≥ 0). Khi đó (1) 2
⇔ t − mt + m −1= 0 (2) ⇔  0.5 (2 điểm) t = m −1
Yêu cầu bài toán ⇔ (1) có 4 nghiệm phân biệt
⇔ (2) có hai nghiệm phân biệt dương ⇔0 < m −1≠1 0.5 m >1 m >1 ⇔  . Vậy  . 0.5 m ≠ 2 m ≠ 2
Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn 10 f ( 3
x + 2x − 2) = 2x −1. Tính tích phân I = f ∫ (x)dx . 1 10 10 Ta có: I = f
∫ (x)dx = f ∫ (t)dt . 0.5 Câu 1 1 1 3 2 Ý b
Đặt t = x + 2x − 2 ⇒ dt = (3x + 2)dx . (2 điểm) 0.5
Đổi cận: t =1⇒ x =1 t =10 ⇒ x = 2 10 2 Khi đó: I = f
∫ (t)dt = f
∫ ( 3x + 2x−2)( 2 3x + 2)dx . 0.5 1 1 2 = ( x − )( 2 x + ) 39 2 1 3 2 dx = ∫ 0.5 2 1 Trang 1/4
Tìm tất cả các giá trị thực của tham số m để phương trình x x 2 25 − 2.10 + 4x m
= 0 có hai nghiệm trái dấu 2x x x x 2 25 − 2.10 + 4x m = 0 (1)  5   5  2 ⇔ − 2 + m =     0  2   2  x 0.5 Đặt 5 t   = >   0 . Phương trình ( ) 1 có dạng:  2  2 2
t − 2t + m = 0 2 2
⇔ m = −t + 2t (2)
Để phương trình (1) có hai nghiệm trái dấu thì phương trình (2) phải Câu 1
có hai nghiệm t ,t thỏa mãn: 0 < t <1< t 0.5 1 2 1 2 Ý c
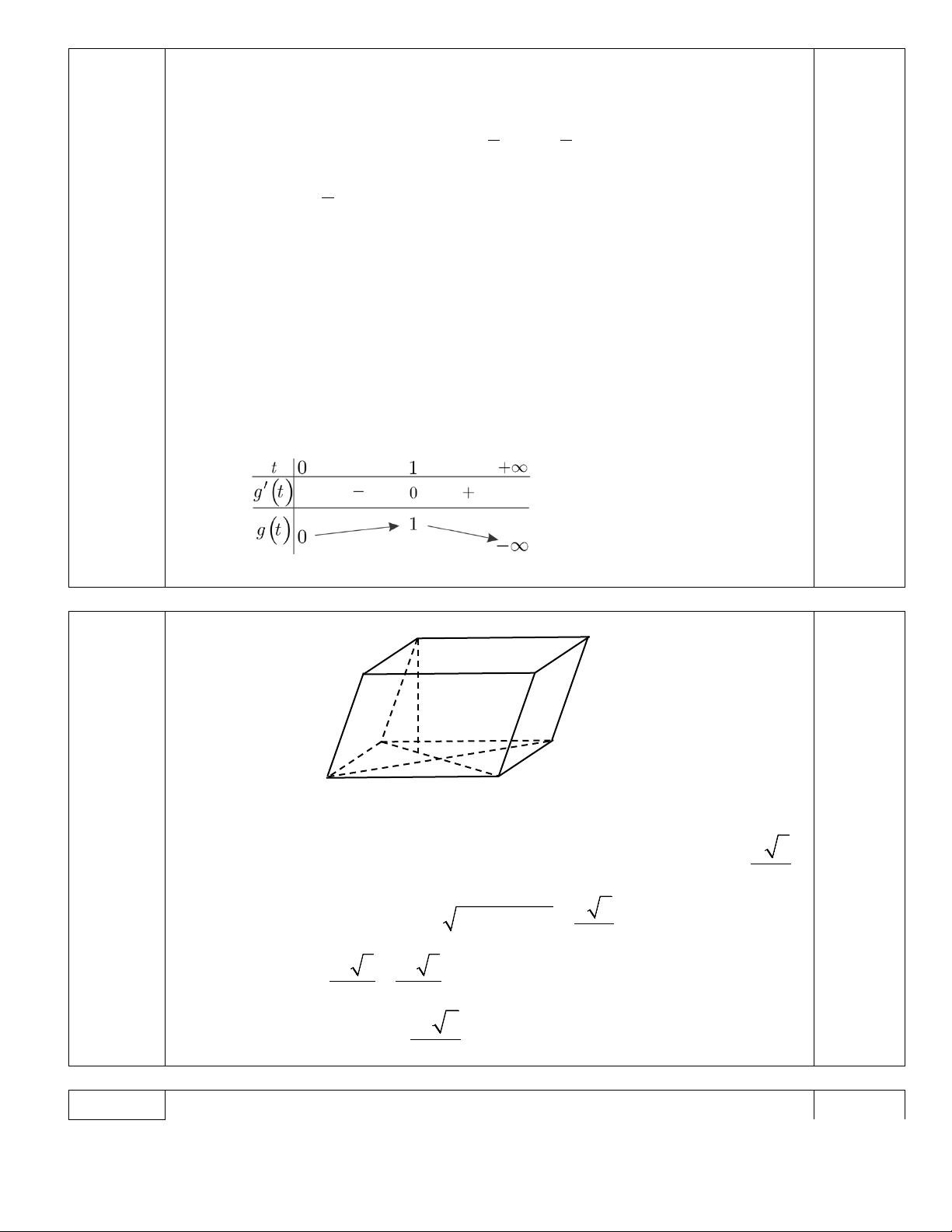
Số nghiệm phương trình (2) là số giao điểm của đồ thị hàm số (2 điểm) g (t) 2
= −t + 2t , t ∈(0;+∞) và đường thẳng 2
d : y = m .
Xét hàm số g (t) 2 = t
− + 2t với t > 0 g′(t) = 2
− t + 2 ; g′(t) = 0 ⇔ t =1; lim g (t) = −∞ t→+∞ 0.5 BBT:
Từ bảng biến thiên suy ra 2
0 < m <1 ⇔ m∈( 1; − 0) ∪(0; ) 1 . 0.5 A' B ' C ' D ' A B H D C Câu 2
Gọi H là trọng tâm của tam giác ABD ⇒ A'H ⊥ ( ABCD) . Ý a 0.5 (2 điểm)  0 BAD = −  0 180
ABC = 60 nên tam giác ABD đều cạnh a 3 ⇒ = a AH 3
∆A' AH vuông tại H 2 2 6 ⇒ ' = ' − = a A H AA AH 0.5 3 2 2 a 3 a 3 S = S = = 0.5 ABCD 2 ABD ∆ 2. 4 23a 2 V = A H S = 0.5 ABCDA B C D ' . ' ' ' ' ABCD 2
Câu 2 b) Trong không gian với hệ tọa độ Oxyz , cho đường thẳng Trang 2/4 Ý b
x − 3 y − 3 z (2 điểm) d : =
= , mặt phẳng (α) : x + y − z + 3 = 0 và điểm A(1;2;−1). 1 3 2
Viết phương trình chính tắc của đường thẳng ∆ đi qua điểm A , cắt
đường thẳng d và song song với mặt phẳng (α). 
Mặt phẳng (α ) có vectơ pháp tuyến n = (1;1;− ) 1  0.5
Gọi M = d ∩ ∆ ⇒ M (3+ t;3+ 3t;2t) ⇒ AM = (2 + t;1+ 3t;2t + ) 1  
∆ / /(α ) ⇒ AM.n = 0 ⇔ t = 1 − 0.5 
Vectơ chỉ phương của đường thẳng ∆ là AM = (1; 2 − ;− ) 1 0.5 − − +
Phương trình chính tắc của x y z ∆ là: 1 2 1 = = . 0.5 1 2 − 1 − 2 2
x  2y  x  y  63xy (1)  3 2  4
x 2x  y  2x 3  12 y (2)  2. Điều kiện 3 x  và 1 y  0.5 2 2
(1) viết lại là x2 +(1-3y)x + 2y2 +y-6 = 0. 0.5 
Do đó x  y  2  . x 0.5  2 y 3 
Vì điều kiện nên ta loại x  2y3. 0.5
Câu 3 Thay y  x2 vào (2) ta được phương trình (4 điểm) 3 2 4
x 2x  x 2  2x 3  52x  0 (3) 0.5 Xét hàm số f(x) =   3 2 4
x 2x  x 2  2x 3  52x  0 với 3 5 x   ;  0.5 2 2   ta có   2 1 1
f '(x)  3x 4x 1  >0 với 3 5 x   ;  4 3
2x 3 2 (52x) 2 2   0.5
nên f(x) đồng biến trên 3 5  ;   2 2
Nhận thấy x  2 là nghiệm của (3). Do đó x  2 là nghiệm duy nhất.
Vậy hệ có nghiệm x, y2,0 0.5
Cho các số thực không âm a,b,c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất của biểu thức
P = ab + 3ac + 5bc .
Theo giả thiết ta có: c =1 −(a + b) ≥ 0 ⇔ 0 ≤ a + b ≤1 0.5 Câu 4
a + c =1− b ≥ 0 ⇔ 0 ≤ b ≤1
(3 điểm) Khi đó ab + 3ac + 5bc = ab + 3c(a + b) + 2bc = ab + 3(1−(a + b))(a + b) + 2b(1− (a + b)
= −(a +b)2 +(a +b) + ( 2 3 2 b
− + b) − ab   0.5 Xét hàm f (x) 2
= −x + x, x ∈[0; ]
1 . Dễ thấy f (x) 1 ≤ x ∀ ∈[0; ] 1 0.5 4 Trang 3/4
Theo chứng minh trên a + b∈[0; ] 1 ; b∈[0; ] 1 0.5
nên f (a + b) 1 ≤ f (b) 1 ; ≤ ;− ab ≤ 0 4 4 Suy ra 1 1 5
ab + 3ac + 5bc ≤ 3. + 2. = 0.5 4 4 4
Dấu đẳng thức xảy ra khi 1
a = 0;b = c = 0.5 2
Có 20 người xếp thành một vòng tròn. Hỏi có bao nhiêu cách chọn ra 5 người
sao cho không có hai người kề nhau được chọn.
Ta giải bài toán tổng quát sau: Có n người xế p thành một hàng dọc. Có bao
nhiêu cách chọn ra k người, sao cho không có hai người kề nhau được chọn?
Giả sử ta chọn được k người. Gọi x1 là số người tính từ người đầu tiên đến
trước người thứ nhất được chọn, x2 là số người giữa người thứ nhất được
chọn và người thứ hai được chọn, …, x 0.5
k là số người giữa người thứ k -1 và
người thứ k được chọn và xk+1 là số người sau người thứ k được chọn đến
cuối. Khi đó ta có : x1 + x2 + … + xk+1 = n – k (1)
Với x1, xk+1 là các số nguyên không âm ; x2, …, xk là các số nguyên ≥ 1.
Ngược lại, nếu (x1, …, xk+1) là một nghiệm của (1) với x1, xk+1 ≥ 0, x2, …, xk ≥
1 thì ta cho tương ứng với cách chọn người thứ 1+x1, 2+x1+x2, …, k+x 0.5
1+…+xk thì rõ ràng do (i + x1 + …+ xi) – (i-1 + x1 + …+xi-1) = 1 + xi ≥ 2
Câu 5 nên không có 2 người liên tiếp được chọn.
(3 điểm) Đặt y1 = x1, yk+1 = xk+1 và yi = xi – 1 với i=2, …, k thì được
y1 + y2 + … + yk+1 = n – 2k + 1 (2) với yi là các số nguyên không âm. 0.5
Theo kết quả định lý chia kẹo của Euler, ta có số nghiệm của (2) bằng k C n−k 1 + .
Giả sử 20 người đó được đánh số 1, 2, …, 20. Ta xét các trường hợp sau :
TH1: Người số 1 được chọn. Khi đó người số 2 và số 20 không được chọn.
Như vậy ta phải chọn thêm 4 người từ 3 đến 19 sao cho không có hai người 0.5
kề nhau được chọn. Vì 19 không kề 3 nên có thể coi đây là 17 người xếp theo
một hàng dọc. Theo kết quả của bài toán trên, số cách chọn bằng C4 . 14
TH2 : Người số 1 không được chọn. Khi đó ta cần chọn 5 người từ số 2 đến
20 sao cho không có 2 người kề nhau được chọn. Vì 2 và 20 không kề nhau
nên có thể coi đây là 19 người xếp theo một hàng dọc. Theo kết quả của bài 0.5
toán trên, số cách chọn bằng C5 . 15 C4 + C5 14 15 =4004 0.5
……………………….Hết……………………… Trang 4/4 UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2017-2018 PHIẾU CHẤM VÒNG 1 Môn: Địa lí
Mã túi………………. ………Số phách……….…….………..………………… Câu 1 Nội dung Điểm Điểm chấm a) Cho hàm số 4 2
y = x − mx + m −1 có đồ thị là (C .Tìm tất cả các giá trị m )
thực của tham số m để đồ thị (C cắt trục hoành tại bốn điểm phân biệt. m )
Phương trình hoành độ giao điểm của (C và trục hoành là: m ) Câu 1 4 2 0.5 Ý a
x − mx + m −1= 0 (1) (2 t =1 2
điểm) Đặt t = x (t ≥ 0). Khi đó (1) 2
⇔ t − mt + m −1= 0 (2) ⇔  0.5 t = m −1
Yêu cầu bài toán ⇔ (1) có 4 nghiệm phân biệt
⇔ (2) có hai nghiệm phân biệt dương ⇔0 < m −1 ≠1 0.5 m >1 m >1 ⇔  . Vậy  . 0.5 m ≠ 2 m ≠ 2
Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn 10 f ( 3
x + 2x − 2) = 2x −1. Tính tích phân I = f ∫ (x)dx . 1 10 10 Ta có: I = f
∫ (x)dx = f ∫ (t)dt . Câu 1 0.5 1 1 Ý b Đặt 3
t = x + x − ⇒ t = ( 2 2 2 d 3x + 2)dx . (2 = ⇒ = 0.5 điểm)
Đổi cận: t 1 x 1 t =10 ⇒ x = 2 10 2 Khi đó: I = f
∫ (t)dt = f
∫ ( 3x + 2x−2)( 2 3x + 2)dx . 0.5 1 1 2 = ( x − )( 2 x + ) 39 2 1 3 2 dx = ∫ 2 0.5 1
Tìm tất cả các giá trị thực của tham số m để phương trình x x 2 25 − 2.10 + 4x m
= 0 có hai nghiệm trái dấu Câu 1 2x x x x 2 x  5   5  2 Ý c
25 − 2.10 + m 4 = 0 (1) ⇔ − 2 + m =     0  2   2  (2 x 0.5 điểm) Đặt 5 t   = >   0 . Phương trình ( ) 1 có dạng:  2  2 2
t − 2t + m = 0 2 2
⇔ m = −t + 2t (2)
Để phương trình (1) có hai nghiệm trái dấu thì phương trình (2) phải 0.5 Trang 1/4
có hai nghiệm t ,t thỏa mãn: 0 < t <1< t 1 2 1 2
Số nghiệm phương trình (2) là số giao điểm của đồ thị hàm số g (t) 2
= −t + 2t , t ∈(0;+∞) và đường thẳng 2
d : y = m .
Xét hàm số g (t) 2 = t
− + 2t với t > 0 g′(t) = 2
− t + 2 ; g′(t) = 0 ⇔ t =1; lim g (t) = −∞ t→+∞ 0.5 BBT:
Từ bảng biến thiên suy ra 2
0 < m <1 ⇔ m∈( 1; − 0) ∪(0; ) 1 . 0.5 A' B ' C ' D ' A B H D C
Câu 2 Gọi H là trọng tâm của tam giác ABD ⇒ A'H ⊥ (ABCD). Ý a (2  0.5 0 BAD = −  0 điểm) 180
ABC = 60 nên tam giác ABD đều cạnh a 3 ⇒ = a AH 3
∆A' AH vuông tại H 2 2 6 ⇒ ' = ' − = a A H AA AH 0.5 3 2 2 a 3 a 3 S = S = = 0.5 ABCD 2 ABD ∆ 2. 4 2 3 a 2 V = A H S = 0.5 ABCDA B C D ' . ' ' ' ' ABCD 2
b) Trong không gian với hệ tọa độ Oxyz , cho đường thẳng x − 3 y − 3 : z d =
= , mặt phẳng (α) : x + y − z + 3 = 0 và điểm A(1;2;−1). 1 3 2
Câu 2 Viết phương trình chính tắc của đường thẳng ∆ đi qua điểm A , cắt
Ý b đường thẳng d và song song với mặt phẳng (α) . (2 
Mặt phẳng (α ) có vectơ pháp tuyến n = (1;1;− ) 1 điểm)  0.5
Gọi M = d ∩ ∆ ⇒ M (3+ t;3+ 3t;2t) ⇒ AM = (2 + t;1+ 3t;2t + ) 1  
∆ / /(α ) ⇒ AM.n = 0 ⇔ t = 1 − 0.5 
Vectơ chỉ phương của đường thẳng ∆ là AM = (1; 2 − ;− ) 1 0.5 Trang 2/4 − − +
Phương trình chính tắc của x y z ∆ là: 1 2 1 = = . 0.5 1 2 − 1 − 2 2
x  2y  x  y  63xy (1)  3 2  4
x 2x  y  2x 3  12 y (2)  2. Điều kiện 3 x  và 1 y  0.5 2 2
(1) viết lại là x2 +(1-3y)x + 2y2 +y-6 = 0. 0.5 
Do đó x  y  2  . x 0.5  2 y 3 
Câu Vì điều kiện nên ta loại x  2y3. 0.5 3
Thay y  x2 vào (2) ta được phương trình (4 3 2 4
x 2x  x 2  2x 3  52x  0 (3) 0.5
điểm) Xét hàm số f(x) =   3 2 4
x 2x  x 2  2x 3  52x  0 với 3 5 x   ;  0.5 2 2   ta có   2 1 1
f '(x)  3x 4x 1  >0 với 3 5 x   ;  4 3
2x 3 2 (52x) 2 2   0.5
nên f(x) đồng biến trên 3 5  ;   2 2
Nhận thấy x  2 là nghiệm của (3). Do đó x  2 là nghiệm duy nhất.
Vậy hệ có nghiệm x, y2,0 0.5
Cho các số thực không âm a,b,c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất của biểu thức
P = ab + 3ac + 5bc .
Theo giả thiết ta có: c =1−(a +b) ≥ 0 ⇔ 0 ≤ a + b ≤1 0.5
a + c =1− b ≥ 0 ⇔ 0 ≤ b ≤1
Khi đó ab + 3ac + 5bc = ab + 3c(a +b) + 2bc = ab +3(1−(a +b))(a +b)+ 2b(1−(a +b)
= −(a +b)2 +(a +b) + ( 2 3 2 b
− + b) − ab   0.5 Câu 4 (3 Xét hàm f (x) 2
= −x + x, x ∈[0; ]
1 . Dễ thấy f (x) 1 ≤ x ∀ ∈[0; ] 1 0.5 điểm) 4
Theo chứng minh trên a + b∈[0; ] 1 ; b∈[0; ] 1 0.5
nên f (a + b) 1 ≤ f (b) 1 ; ≤ ;− ab ≤ 0 4 4 Suy ra 1 1 5
ab + 3ac + 5bc ≤ 3. + 2. = 0.5 4 4 4
Dấu đẳng thức xảy ra khi 1
a = 0;b = c = 0.5 2
Có 20 người xếp thành một vòng tròn. Hỏi có bao nhiêu cách chọn ra 5 người
Câu 5 sao cho không có hai người kề nhau được chọn. (3
Ta giải bài toán tổng quát sau: Có n người xếp thành một hàng dọc. Có bao điểm)
nhiêu cách chọn ra k người, sao cho không có hai người kề nhau được chọn? 0.5
Giả sử ta chọn được k người. Gọi x1 là số người tính từ người đầu tiên đến Trang 3/4
trước người thứ nhất được chọn, x2 là số người giữa người thứ nhất được chọn
và người thứ hai được chọn, …, xk là số người giữa người thứ k -1 và người
thứ k được chọn và xk+1 là số người sau người thứ k được chọn đến cuối. Khi
đó ta có : x1 + x2 + … + xk+1 = n – k (1)
Với x1, xk+1 là các số nguyên không âm ; x2, …, xk là các số nguyên ≥ 1.
Ngược lại, nếu (x1, …, xk+1) là một nghiệm của (1) với x1, xk+1 ≥ 0, x2, …, xk ≥
1 thì ta cho tương ứng với cách chọn người thứ 1+x1, 2+x1+x2, …, k+x 0.5
1+…+xk thì rõ ràng do (i + x1 + …+ xi) – (i-1 + x1 + …+xi-1) = 1 + xi ≥ 2
nên không có 2 người liên tiếp được chọn.
Đặt y1 = x1, yk+1 = xk+1 và yi = xi – 1 với i=2, …, k thì được
y1 + y2 + … + yk+1 = n – 2k + 1 (2) với yi là các số nguyên không âm. 0.5
Theo kết quả định lý chia kẹo của Euler, ta có số nghiệm của (2) bằng k C n−k 1 + .
Giả sử 20 người đó được đánh số 1, 2, …, 20. Ta xét các trường hợp sau :
TH1: Người số 1 được chọn. Khi đó người số 2 và số 20 không được chọn.
Như vậy ta phải chọn thêm 4 người từ 3 đến 19 sao cho không có hai người kề 0.5
nhau được chọn. Vì 19 không kề 3 nên có thể coi đây là 17 người xếp theo
một hàng dọc. Theo kết quả của bài toán trên, số cách chọn bằng C4 . 14
TH2 : Người số 1 không được chọn. Khi đó ta cần chọn 5 người từ số 2 đến
20 sao cho không có 2 người kề nhau được chọn. Vì 2 và 20 không kề nhau
nên có thể coi đây là 19 người xếp theo một hàng dọc. Theo kết quả của bài 0.5
toán trên, số cách chọn bằng C5 . 15 C4 + C5 14 15 =4004 0.5
Tổng điểm toàn bài: …………………………..điểm.
Bằng chữ: ……………………………………. ………………..
Lai Châu, ngày……………. tháng ………….năm 2018
CÁN BỘ CHẤM THI LẦN 1
(Ký, ghi rõ họ tên) Trang 4/4
Document Outline

• DE CHINH THUC
• DAP AN CHINH THUC
• PHIEU CHAM