PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI LỚP 8 CẤP HUYỆN HUYỆN CỦ CHI Ngày 04 tháng 04 năm 2016 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang) ĐỀ BÀI
Câu 1 (2 điểm): Phân tích đa thức thành nhân tử a) 2 x  x  6 b) 3 2 x  x 14x  24 3 3 x 14 2 x  3x  36
Câu 2 (3 điểm): Cho biểu thức A = 3 3 x 19 2 x  33x  9
a) Tìm giá trị của x để biểu thức A xác định.
b) Tìm giá trị của x để biểu thức A có giá trị bằng 0.
c) Tìm giá trị nguyên của x để biểu thức A có giá trị nguyên.
Câu 3 (5 điểm): Giải phương trình: a) ( 2 x  x)2  4( 2 x  x)  12 x  1 x  2 x  3 x  4 x  5 x  6 b)      2008 2007 2006 2005 2004 2003 c) 6 4 x  5 3 x  38 2
x  5x  6  0 (phương trình có hệ số đối xứng bậc 4) Câu 4 (4 điểm):
a) Tìm GTNN: x 2  5y2  2xy  4x  8y  2015 ( 3 x  ) 1 b) Tìm GTLN: 3 2 x  x  x  1
Câu 5 (6 điểm) Cho tam giác ABC nhọn, các đường cao AA’, BB’, CC’, H là trực tâm. HA' H ' B HC' a) Tính tổng   AA' B ' B CC'
b) Gọi AI là phân giác của tam giác ABC; IM, IN thứ tự là phân giác của góc AIC và góc
AIB. Chứng minh rằng: AN.BI.CM = BN.IC.AM.
c) Chứng minh rằng đường thẳng DF luôn đi qua một điểm cố định khi điểm M di động trên đoạn thẳng AB. ___*HẾT*___
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN HỌC SINH GIỎI LỚP 8 CẤP HUYỆN HUYỆN CỦ CHI Ngày 04 tháng 04 năm 2016 Môn thi: TOÁN
Câu 1 (2 điểm): Phân tích đa thức thành nhân tử a) 2 x  x  6 (1 điểm) = 2 x  2x  3x  6 = x(x  ) 2  ( 3 x  ) 2 = (x  ) 3 (x  ) 2 b) 3 2
x  x 14x  24 (1 điểm) = 3 x  2 2 2 x  x  2x  12x  24 = 2
x (x  2)  x(x  2) 12x(x  2) = (x  2)( 2 x  x 12) = (x  2)( 2 x  4x  3x 12) = (x  2)(x  4)(x  ) 3 3 3 x 14 2 x  3x  36
Câu 2 (3 điểm): Cho biểu thức A = 3 3 x 19 2 x  33x  9 a) ĐKXĐ: 3 3 x 19 2
x  33x  9  0 (1 điểm) 1  x  và x  3 3 3 3 x 14 2 x  3x  36 b) (1 điểm) 3 3 x 19 2 x  33x  9 2 (x  ) 3 3 ( x  4) = 2 3 ( x  ) 1 (x  ) 3 3x  4 = 3x 1 A = 0  3x + 4 = 0  4  x = ( thỏa mãn ĐKXĐ) 3  4 Vậy với x = thì A = 0. 3 3x  4 3x 1  5 5 c) A = = = 1 + (1 điểm) 3x 1 3x 1 3x 1 5 Vì x  Z  A  Z   Z  3x – 1  Ư(5) 3x 1 mà Ư(5) = {-5;-1;1;5} 3x – 1 -5 -1 1 5
x -4/3 (loại) 0 (nhận) 2/3 (loại) 2 (nhận)
Vậy tại x  {0;2} thì A  Z.
Câu 3 (5 điểm): Giải phương trình: a) ( 2 x  x)2  4( 2 x  x)  12 (1 điểm)
Giải phương trình ta được tập nghiệm S = {-2;1} x  1 x  2 x  3 x  4 x  5 x  6 b)      (2 điểm) 2008 2007 2006 2005 2004 2003 x  1 x  2 x  3 x  4 x  5 x  6  1 1  1  1 1 1 2008 2007 2006 2005 2004 2003 x  2009 x  2009 x  2009 x  2009 x  2009 x  2009       2008 2007 2006 2005 2004 2003 x  2009 x  2009 x  2009 x  2009 x  2009 x  2009        0 2008 2007 2006 2005 2004 2003 1 1 1 1 1 1  (x  2009)(      )  0 2008 2007 2006 2005 2004 2003 1 1 1 1 1 1  x  2009  0 vì (       0) 2008 2007 2006 2005 2004 2003  x = -2009
Vậy tập nghiệm của phương trình là S = {-2009} c) 6 4 x  5 3 x  38 2
x  5x  6  0 (2 điểm)  Chia cả 2 vế cho 2 x , ta được: 2 5 6 6x  5x  38    0 2 x x 2 1 1  6(x  )  ( 5 x  )  38  0 (*) 2 x x 1 1  Đặt x  = y => 2 x  = 2 y x 2 x
Thay vào phương trình (*) rồi giải phương trình, ta được 1 1
Tập nghiệm của phương trình là: {-2; ;0; } 2 3 Câu 4 (4 điểm):
a) Tìm GTNN: P= x 2  5y2  2xy  4x  8y  2015 ( 3 x  ) 1 b) Tìm GTLN: Q= 3 2 x  x  x  1
a) P = x2  5y2  2xy  4x  8y  2015 (2 điểm)
P = x2 + 5y2 + 2xy – 4x – 8y + 2015
P = (x2 + y2 + 2xy) – 4(x + y) + 4 + 4y2 – 4y + 1 + 2010
P = (x + y – 2)2 + (2y – 1)2 + 2010  2010 3 1
=> Giá trị nhỏ nhất của P = 2010 khi x  ; y  2 2 ( 3 x  ) 1 b) Q = (2 điểm) 3 2 x  x  x  1 = ( 3 x  ) 1 2 x (x  ) 1  (x  ) 1 = ( 3 x  ) 1 ( 2 x  ) 1 (x  ) 1 = 3 2 x  1 Q đạt GTLN  2 x 1 đạt GTNN Mà 2 x 1  1 => 2
x 1 đạt GTNN là 1 khi x = 0.
=> GTLN của C là 3 khi x = 0.
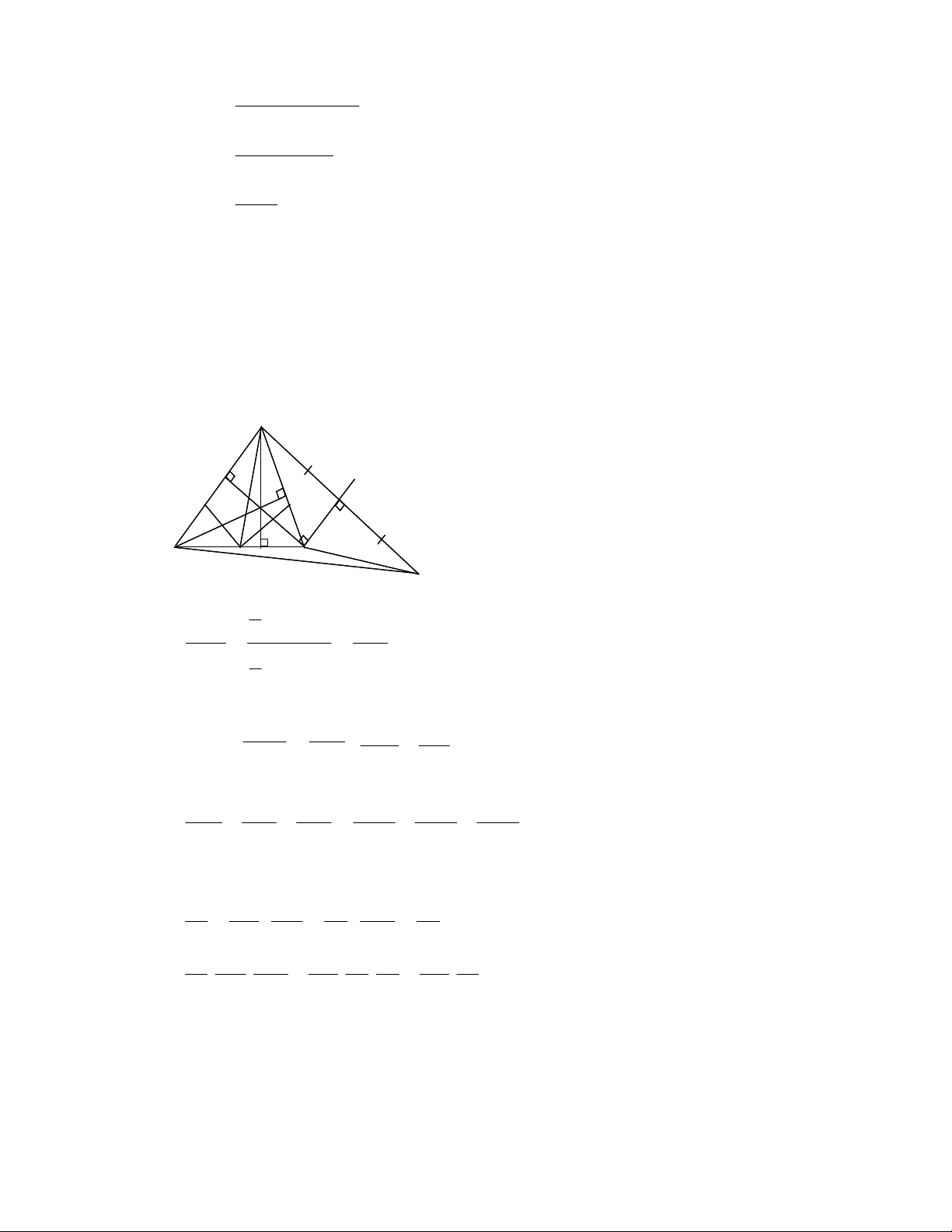
Câu 5 (6 điểm): Vẽ hình đúng (0,5điểm) A C’ C B’ x ’ H N M I A’ A C B D 1 H . A' B . C S HA' HBC 2 a)   S 1 AA' ; (0,5điểm) ABC A . A' B . C 2 S H ' C HAB S H ' B Tương tự:  HAC  S CC' ; (0,5điểm) ABC S B ' B ABC HA' H ' B H ' C S S S HBC HAB HAC      1 A ' A B ' B C ' C S S S (0,5điểm) ABC ABC ABC
b) Áp dụng tính chất phân giác vào các tam giác ABC, ABI, AIC: BI AB AN AI CM IC  ;  ;  (0,5điểm ) IC AC NB BI MA AI BI AN CM AB AI IC AB IC . .  . .  . 1 IC NB MA AC BI AI AC BI (0,5điểm )  BI A . N C . M  BN I.C A . M
c)Vẽ Cx  CC’. Gọi D là điểm đối xứng của A qua Cx (0,5điểm)
-Chứng minh được góc BAD vuông, CD = AC, AD = 2CC’ (0,5điểm)
- Xét 3 điểm B, C, D ta có: BD  BC + CD (0,5điểm)
-  BAD vuông tại A nên: AB2+AD2 = BD2
 AB2 + AD2  (BC+CD)2 (0,5điểm) AB2 + 4CC’2  (BC+AC)2 4CC’2  (BC+AC)2 – AB2
Tương tự: 4AA’2  (AB+AC)2 – BC2
4BB’2  (AB+BC)2 – AC2 (0,5điểm)
-Chứng minh được : 4(AA’2 + BB’2 + CC’2)  (AB+BC+AC)2 (AB  BC  CA)2  4 (0,5điểm)  A A'2  B ' B 2  CC'2
(Đẳng thức xảy ra  BC = AC, AC = AB, AB = BC  AB = AC =BC   ABC đều)