Đề Thi Học Sinh Giỏi Toán 8 Cấp Huyện Năm 2025-2026 Có Đáp Án

ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 8 Năm học 2025- 2026 MÔN: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
(Đề thi gồm 05 câu, trong 01 trang) Câu 1: (5 điểm)
1. Phân tích đa thức thành nhân tử: (x − 3). (x − 5). (x − 6). (x − 10) − 24x2 2. Cho biểu thức: x2 − 5x 25 − x2 x + 3 x − 5 A = ( − 1) : ( − + ) x2 − 25 x2 + 2x − 15 x + 5 x − 3 a. Rút gọn A.
b. Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
c. Tìm Điều kiện của x đề A > 0 Câu 2: (3,5 điểm)
1. Cho a, b, c đôi một khác nhau thỏa mãn: ab + bc + ca = 1
Tính giá trị của biểu thức : (a+b)2.(b+c)2.(c+a)2 A = (1+a2).(1+b2).(1+c2)
2. Tìm số dư khi chia đa thức A = (x + 1)(x + 3)(x + 5)(x + 7) + 2028 chia cho đa thức x2 + 8x + 12 Câu 3: (3,5 điểm)
1. Tìm các số nguyên x, y thỏa mãn : x2 − 656xy − 657y2 = 1983 2. Giải phương trình: x − 241 x − 220 x − 195 x − 166 + + + = 10 17 19 21 23
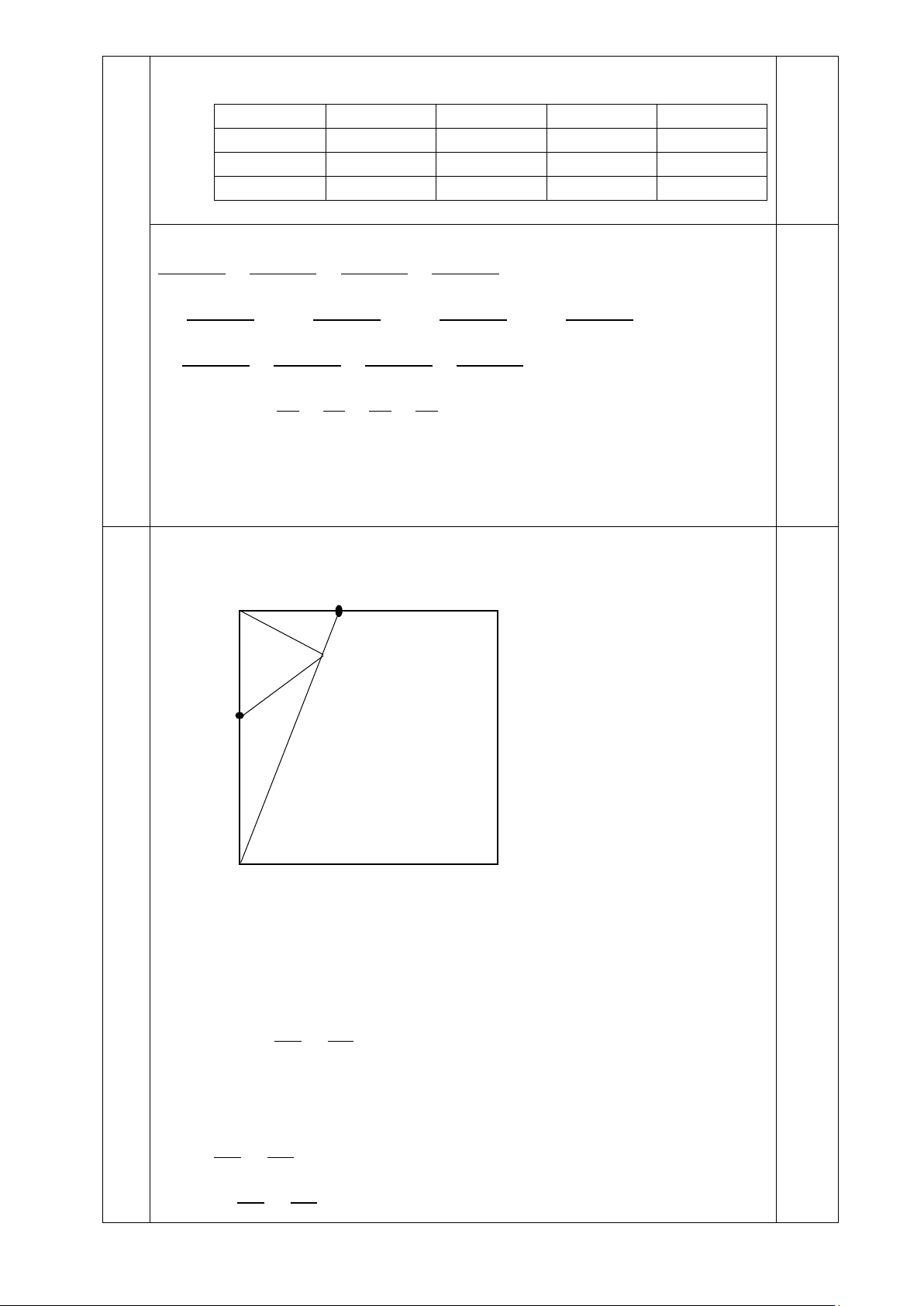
Câu 4 (6 điểm): Cho hình vuông ABCD và các điểm E, F lần lượt trên các cạnh AB, AD sao
cho AE = AF. H là hình chiếu trên DE a. Chứng minh AD2 = DH . DE
b. Chứng minh hai tam giác AHF và DHC đồng dạng.
c. Xác định vị trí của các điểm E và F để diện tích ∆CDh gấp 9 lần diện tích ∆AFH. Câu 5: (2 điểm)
1. Chứng minh rằng A = n8 + 4n7 + 6n6 + 4n5 + n4 chia hết cho 16
2. Cho a, b, c > 0. Chứng minh rằng: a2 b2 c2 a3 + b3 + c3 + +  b2 + c2 c2 + a2 a2 + b2 2abc
…………………..HẾT…………………… ĐÁP ÁN: câu ĐÁP ÁN Điểm 1 1. (1,5 điểm)
(x − 3). (x − 5). (x − 6). (x − 10) − 24x2
= (x2 − 13x + 30)(x2 − 11x + 30) − 24x2 0,25 Trang 1
= [(x2 − 12x + 30) − x]. [(x2 − 12x + 30) + x] − 24x2 0,25 =(x2 − 12x + 30)2 − 25x2 0,25
= (x2 − 12x + 30 − 5x). (x2 − 12x + 30 + 5x)
= (x2 − 17x + 30). (x2 − 7x + 30) 0,5
= (x2 − 2x − 15x + 30). (x2 − 7x + 30)
= (x − 2)(x − 15)(x2 − 7x + 30) 0,25
2. a. (1,5 điểm) ĐKXĐ : x # ± 5; x # 3 0,25 x2 − 5x 25 − x2 x + 3 x − 5 A = ( − 1) : ( − + ) x2 − 25 x2 + 2x − 15 x + 5 x − 3 x(x − 5)
25 − x2 − (x + 3)(x − 3) + (x − 5)(x + 5) = ( − 1) : ( ) 0,5 (x − 5)(x + 5) (x − 3)(x + 5) x
25 − x2 − x2 + 9 + x2 − 25 = ( − 1) : ( ) x + 5 (x − 3)(x + 5) 0,25 5 (3 − x)(x + 3) = : x + 5 (x + 5)(x − 3) 5 x + 5 0,25 = . (− ) x + 5 x + 3 0,25 b. b.(1 điểm)
Để A nguyên thì x + 3  Ư(−5) = {−5 ; −1 ; 1 ; 5} 0,5
Vậy x {−8; −4; −2; 2} 0,5 c. A > 0  x + 3 < 0 0,5  x < - 3 0,5 2 1. (1,5 điểm) (a + b)2. (b + c)2. (c + a)2 A = (1 + a2). (1 + b2). (1 + c2) (a + b)2(b + c)2(c + a)2 = 0,5
(ab + bc + ca + a2)(ab + bc + ca + b2)(ab + bc + ac + c2) (a + b)2(b + c)2(c + a)2 A = = 1 1,0
(a + b)(a + c)(b + c)(a + b)(a + c)(b + c)
2. A = (x + 1)(x + 3)(x + 5)(x + 7) + 2028
A = (x2 + 8x + 7). (x2 + 8x + 15) + 2028 0,25 Đặt t = x2 + 8x + 11 0,25 A = (t − 4)(t + 4) + 2028 A = t2 − 16 + 2028 A = t2 + 2012 A = (x2 + 8x + 11)2 + 2012 0,5
A = [(x2 + 8x + 12) − 1]2 + 2012 0,25
A = (x2 + 8x + 12) − 2. (x2 + 8x + 12) + 2013
Vậy số dư trong phép chia đa thức A cho đa thức x2 + 8x + 12 dư 2013 0,25 3 1. (1,5 điểm) x2 − 656xy − 657y2 = 1983
 x2 − 656xy − y2 − 656y2 = 1983
(x2 − y2) − 656(xy + y2) = 1983 0,5
(x − y)(x + y) − 656y(x + y) = 1983 Trang 2
(x + y)(x − 657y) = 3.661 = 661.3 = (−3). (−661) 0,25 = (−661). (−3) x + y 3 661 -3 -661 x - 657y 661 3 -661 -3 0,25 x 4 660 -4 -660 y -1 1 1 -1 0,25
Vậy (x; y) = {(4; -1); (-4; 1); (660; 1); (-660; -1)} 2. (2 điểm) x − 241 x − 220 x − 195 x − 166 + + + = 10 17 19 21 23 x − 241 x − 220 x − 195 x − 166  0,5 − 1 + − 2 + − 3 + + 4 = 0 17 19 21 23 x − 258 x − 258 x − 258 x − 258  + + + = 0 17 19 21 23 1 1 1 1  (x − 258) ( + + + ) = 0 17 19 21 23 0,5 x − 258 = 0  x = 258 0,25
Vậy phương trình có nghiệm x = 258 0,25 4 A E B F C D a. (2 điểm)
Xét ∆ADE vuông tại A và ∆HDA vuông tại H có 0,5 ADE ̂ chung
Nên ∆ADE đồng dạng ∆HDA (g.g) 0,5 AD DE suy ra = DH AD 0,5 AD2 = DE . DH b. (2 điểm) 0,5
Vì ∆ADE đồng dạng ∆HDA nên AD AE 0,5 = DH AH DC AF 0,5  = (do AD = DC; AE = AF) DH AH 0,5 Trang 3 Mà HDC ̂ = HAD ̂ (cùng phụ góc HAD)
Suy ra ∆AHF đồng dạng ∆DHC c. (2 điểm)
Ta có ∆CDH đồng dạng ∆AFH nên : S∆CDH CD 0,5 = ( )2 S ∆AFH AF S CD 0,5  ∆CDH = 9( )2 = 9 S ∆AFH AF CD = 3 AF. 0,5
Vậy để diện tích ∆CDH gấp 9 lần diện tích ∆AFH thì E, F thuộc
AB, AD sao cho AE = AF = 1/3 AB. 0,5 5
1. Chứng minh rằng A = n8 + 4n7 + 6n6 + 4n5 + n4 chia hết cho 16 A = n8 + 4n7 + 6n6 + 4n5 + n4
A = n8 + n7 + 3n7 + 3n6 + 3n6 + 3n5 + n5 + n4
A = n7(n + 1) + 3n6(n + 1) + 3n6(n + 1) + n4(n + 1)
A = (n + 1)n4(n3 + 3n2 + 3n + 1) A = (n(n + 1)2)4 0,5
Vì n.(n + 1) là tích của hai số nguyên liên tiếp nên n. ( n + 1) ⁝ 2
Suy ra (n(n + 1)2)4 ⁝ 24 = 16 0,5 2. Chứng minh rằng: a2 b2 c2 a3 + b3 + c3 + +  b2 + c2 c2 + a2 a2 + b2 2abc Ta có: a2  𝑎2 b2 + c2 2𝑏𝑐 b2 𝑏2 ≤ c2 + a2 2𝑎𝑐 0,5 c2 𝑐2 ≤ a2 + b2 2𝑎𝑏 Cộng từng vế ta có: a2 b2 c2 𝑎2 𝑏2 𝑐2 a3 + b3 + c3 + + ≤ + + ≤ 0,25 b2 + c2 c2 + a2 a2 + b2 2𝑏𝑐 2𝑎𝑐 2𝑎𝑏 2abc + 0,25 Trang 4