Đề thi học sinh giỏi Toán 8 năm 2014 – 2015 phòng GD&ĐT Ý Yên – Nam Định

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi học sinh giỏi Toán 8 năm 2014 – 2015 phòng GD&ĐT Ý Yên – Nam Định; đề thi có đáp án và lời giải.

Trích dẫn đề thi học sinh giỏi Toán 8 năm 2014 – 2015 phòng GD&ĐT Ý Yên – Nam Định:
+ Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.
1) Chứng minh EDA = EBC.
2) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD + CM.CA có giá trị không đổi.
+ Cho tam giác ABC. Gọi M là điểm bất kì trên cạnh AC, qua M kẻ các đường thẳng ME, MF lần lượt song song với cạnh AB, BC (E thuộc BC và F thuộc AB). Tìm vị trí của M để diện tích tứ giác BEMF có diện tích lớn nhất.
+ Tìm giá trị nguyên của x để biểu thức Q = 2.P nhận giá trị nguyên.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 8

Môn: Toán 8

Thông tin:

5 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
PHÒNG GIÁO DỤC - ĐÀO TẠO
HUYỆN Ý YÊN
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THCS
NĂM HỌC 2014 - 2015
MÔN : TOÁN – LỚP 8
Thời gian làm bài: 150 phút
Đề gồm 01 trang
Bài 1. (3 điểm)
1) Phân tích đa thức thành nhân tử:
2 2 2
x y z y z x z x y
.
2) Cho
2 2 2
2 2 2
4
x y y z z x x y z xy yz zx
.
Chứng minh rằng
x y z
.
Bài 2. (4 điểm) Cho biểu thức
P
2 2
2 2 3 2
2 2 1 2
. 1
2 4 8 4 2
x x x
x x x x x x
, với
0; 2
x x
.
1) Rút gọn P.
2) Tìm giá trị nguyên của x để biểu thức Q = 2.P nhận giá trị nguyên.
Bài 3. (4 điểm) Giải phương trình
1)
3 3
4,5 5,5 12,25
x x
2)
2 2 2
6 12 7
3
2 8 3
x x x
.
Bài 4. (2 điểm) Cho các số dương x, y, z thỏa mãn
1 1 1
4
x y z
. Chứng minh
1 1 1
1
2 2 2
x y z x y z x y z
.
Bài 5. (5 điểm)
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C
vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia
BA tại E.
1) Chứng minh
EDA EBC
.
2) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD +
CM.CA có giá trị không đổi.
Bài 6. (2 điểm)
Cho tam giác ABC. Gọi M là điểm bất kì trên cạnh AC, qua M kẻ các đường
thẳng ME, MF lần lượt song song với cạnh AB, BC ( E
BC và F
AB). Tìm vị trí
của M để diện tích tứ giác BEMF có diện tích lớn nhất.
Họ và tên thí sinh: …………………
Số báo danh:…………………………
Họ, tên chữ ký GT 1: ………………………….
Họ, tên chữ ký GT 2: ………………………….
ĐỀ CHÍNH THỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HUYỆN
Ý YÊN
HƯỚNG DẪN CHẤM TOÁN 8
NĂM HỌC 2014 – 2015
Bài
ý
N
ội dung đáp án
Đi
ểm
1
(3,0đ)
1)
(1,5đ)
2 2 2
x y z y z x z x y
=
2 2 2
x y z y z x z x z z y
0,5
=
2 2 2 2
x y z y z x z x z z y z
0,25
=
2 2 2 2
y z x z z x y z
0,25
y z x z x z z x y z y z
0,25
y z x z x z z y y z x z x y
0,25
2)
(1,5đ)
2 2 2
2 2 2
4
x y y z z x x y z xy yz zx
2 2 2 2 2 2
2 2 2
2 2 2
4 4 4 4 4 4
x xy y y yz z z xz x
x y z xy yz xz
0,25
2 2 2
2 2 2 2 2 2 0
x y z xy yz xz
0,25
2 2 2 2 2 2
2 2 2 0
x xy y y yz z z xz x
2 2 2
0
x y y z z x
0,5
Mà
2
0
x y
;
2
0
y z
;
2
0
z x
với mọi x, y ,z
0,25
nên
2 2 2
0
x y y z z x
khi và chỉ khi x= y; y =z ; z =x
hay x = y = z ( đpcm).
0,25
2
(4,0đ
)
1
(2,5đ
)
ĐK:
0; 2
x x
0,25
P
2
2
2 2 2
2 2
2 2
.
2 4 2 4 2
x x x
x x x
x x x x x
0,5
2
2
2
2
2 4 1 2
.
2 4 2
x x x x x
x
x x
0,5
2
2 2
2 4 1
2 4 .
x x x x
x x
0,5
2
2
4 4 4 1
2 4
x x x x
x x
0,25
2
2
4 1
1
2
2 4
x x
x
x
x x
0,5
2
(1,5đ)
Có
1 1
2. 1
x
Q P
x x
0,5
Vơi
0; 2
x x
;
x
, để Q nhận giá trị nguyên khi và chỉ khi x là Ư(1)
Mà Ư(1) =
1;1
0,5
1 ; 1
x x
( thỏa mãn ĐK)
0,25
V
ậy giá trị
x
c
ần t
ìm là:
1; 1.
0,25
3.
(4,0đ)
1)
(2,0đ)
3 3
4,5 5,5 12,25
x x
Đặt y = x
5, phương trình trở thành
3 3
0,5 0,5 12,25
y y
0,25
3 2 2 3 3 2 2 3
3. .0,5 3. .0,5 0,5 3. .0,5 3. .0,5 0,5 12,25
y y y y y y
0,25
2
3 0,25 12,25 0
y
0,25
3 2 2 0
y y
2
2
y
y
0,5
Với y = 2 , ta được : x = 7
V
ới y =
2 , ta đư
ợc x = 3
0,5
V
ậy nghiệm của ph
ương tr
ình
là
: x= 3
; x= 7.
0,25
2)
(2 đ)
2 2 2
6 12 7
3
2 8 3
x x x
2 2 2
6 12 7
1 1 1 0
2 8 3
x x x
0,5
2 2 2
2 2 2
4 4 4
0
2 8 3
x x x
x x x
2
2 2 2
1 1 1
4 0
2 8 3
x
x x x
(1)
0,5
Có
2 2 2
1 1 1
0
2 8 3
x x x
với mọi giá trị của x.
0,25
Nên (1)
2
2
4 0 2 2 0
2
x
x x x
x
0,5
V
ậy ph
ương tr
ình có hai nghi
ệm :
x =
2 ;
x
=
2.
0,25
4.
(2,0 đ)
C/m: Với x, y là số dương và a, b là số bất kì. Ta có
2
2 2
a b
a b
x y x y
0,5
Áp d
ụng kết quả tr
ên, ta có:
0,5
2
2 2 2 2 2 2
1 1
1 1
1
2 2
4 4
2
1 1 1 1 1 1 1 1
1 1
4 4 4 4 4 4 4 4
4 4
1 1 2 1 1
2 16
x y x x y x z x y x z
x y x z x y x z x y x z
x y x x y z
Tương tự cũng có:
1 1 1 2 1 1 1 1 1 2
;
2 16 2 16
x y z x y z x y z x y z
0,25
1 1 1 1 2 1 1 1 1 2 1 2 1
2 2 2 16
1 1 1 1 4 4 4 1 1 1 1
2 2 2 16 4
x y x x y z x y z x y z x y z x y z
x y x x y z x y z x y z x y z
0,5
Theo bài ra
1 1 1
4
x y z
1 1 1
1
2 2 2
x y x x y z x y z
(đpcm)
0,25
5.
(5,0đ)
1)
(2,5đ)
-
Ch
ứng minh
EBD ~
ECA (gg)
0,75
EB ED
EC EA
( hai cạnh tương ứng)
0,5
Ch
ứng minh:
EAD ~
ECB (c.g.c)
0,75
EDA EBC
( hai góc tương ứng)
0,5
2)
(2,5đ)
Kẻ MI
BC.
Ch
ứng minh
BMI ~
BCD (g.g)
0,75
BM BI
BC BD
( hai cạnh tương ứng)
. .
BM BD BC BI
0,5
Tương t
ự có
. .
CM AC BC IC
0,5
Cộng vế với vế, ta được
. . . .BM BD CM CA BC BI BC CI BC BI IC
BC
2
0,75
Mà BC không đ
ổi => đpcm
A
B
C
E
M
I
D
6.
(2,0đ)
Ta có ME // AB (gt) và MF // BC (gt)
ME // BF và MF // BE
Tứ giác BEMF là hình bình hành ( hai cặp cạnh đối song song)
0,25
Kẻ AH
BC tại H , AH cắt MF tại G.
Ta có
1
.
2
ABC
S AH BC
và
.
BEMF
S HG FM
nên
2. .
BEMF
ABC
S HG FM
S AH BC
0,25
Gọi AM = x; MC = y
AC = x + y
Xét
ABC có MF // BC (gt)
FM AM
BC AC
( hệ quả định lí Talet)
FM x
BC x y
0,25
Xét
AHC có GM //HC
HG CM
AH AC
( định lí Talet)
HG y
AH x y
0,25
Do đó
2
2.
BEMF
ABC
S xy
S
x y
Ta có :
2 2
2
1
0 4
4
xy
x y x y xy
x y
0,5
1 1
2. .
4 2
BEMF
BEMF ABC
ABC
S
S S
S
0,25
Mà
ABC
S
không đổi nên
BEMF
S đạt giá trị lớn nhất là
1
.
2
ABC
S
khi và chỉ khi x =
y
Hay M là trung đi
ểm của AC.
0,25
G
A
B
C
M
E
F
H
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GIÁO DỤC - ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THCS HUYỆN Ý YÊN NĂM HỌC 2014 - 2015 ĐỀ CHÍNH THỨC MÔN : TOÁN – LỚP 8
Thời gian làm bài: 150 phút Đề gồm 01 trang Bài 1. (3 điểm)
1) Phân tích đa thức thành nhân tử: 2    2     2 x y z y z x  z x  y .
2) Cho x  y 2   y  z 2   z  x 2   2 2 2
4 x  y  z  xy  yz  zx  .
Chứng minh rằng x  y  z .
Bài 2. (4 điểm) Cho biểu thức 2 2  x  2x 2x   1 2  P   . 1     , với x  0; x  2 . 2 2 3 2
 2x  4 8  4x  2x  x   x x  1) Rút gọn P.
2) Tìm giá trị nguyên của x để biểu thức Q = 2.P nhận giá trị nguyên.
Bài 3. (4 điểm) Giải phương trình 1)  x  3  x  3 4,5 5,5  12,25 6 12 7 2)   3  . 2 2 2 x  2 x  8 x  3
Bài 4. (2 điểm) Cho các số dương x, y, z thỏa mãn 1 1 1    4 . Chứng minh x y z 1 1 1    1 . 2x  y  z x  2 y  z x  y  2z Bài 5. (5 điểm)
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C
vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. 1) Chứng minh E  DA  E  BC.
2) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD +
CM.CA có giá trị không đổi. Bài 6. (2 điểm)
Cho tam giác ABC. Gọi M là điểm bất kì trên cạnh AC, qua M kẻ các đường
thẳng ME, MF lần lượt song song với cạnh AB, BC ( EBC và FAB). Tìm vị trí
của M để diện tích tứ giác BEMF có diện tích lớn nhất.
Họ và tên thí sinh: …………………
Họ, tên chữ ký GT 1: ………………………….
Số báo danh:………………………… Họ, tên chữ ký GT 2: ………………………….
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HUYỆN HƯỚNG DẪN CHẤM TOÁN 8 Ý YÊN NĂM HỌC 2014 – 2015 Bài ý Nội dung đáp án Điểm 1 2    2     2 x y z y z x  z  x  y = (3,0đ) 0,5 2    2     2 x y z
y z x  z  x  z  z  y 2 2 2 2
1) = x  y  z  y  z  x  z  x  z  z  y  z 0,25 (1,5đ) =    2 2       2 2 y z x z z x y  z  0,25
  y  z x  z x  z   z  x y  z y  z 0,25
  y  z x  z x  z  z  y   y  z x  z x  y 0,25
2) x  y 2   y  z 2  z  x 2   2 2 2
4 x  y  z  xy  yz  zx  (1,5đ) 2 2 2 2 2 2
 x  2xy  y  y  2yz  z  z  2xz  x 2 2 2
 4x  4y  4z  4xy  4yz  4xz 0,25 2 2 2
 2x  2y  2z  2xy  2yz  2xz  0 0,25   2 2 x  xy  y    2 2 y  yz  z    2 2 2 2 z  2xz  x   0 0,5
  x  y2   y  z2   z  x2  0
Mà  x  y2  0 ;  y  z2  0 ;  z  x2  0 với mọi x, y ,z 0,25
nên x  y 2   y  z 2   z  x2  0 khi và chỉ khi x= y; y =z ; z =x 0,25 hay x = y = z ( đpcm). 2 (4,0đ) ĐK: x  0; x  2 0,25
  2x  2xx 2 2 2x  x  x  2 0,5 P      2   . 2 x  4x  2  2 x  4x  2 2  x  1 x x  22 2  4x x   1  x  2  (2,5đ) 0,5 2 . 2 x  4x  2 2 x x 
 x22 4xx 1    0,5 2 2 x  4 2 .x
 2x 4x  4 4xx 1  0,25 2x  2 x  4  2x 4x 1  x 1   0,5 2x  2 x  4 2x Có x  1 1 Q  2.P   1  0,5 x x
2 Vơi x  0; x  2 ; x , để Q nhận giá trị nguyên khi và chỉ khi x là Ư(1) 0,5
(1,5đ) Mà Ư(1) =1;  1
 x  1 ; x  1 ( thỏa mãn ĐK) 0,25
Vậy giá trị x cần tìm là: 1; 1. 0,25 3. x  3  x  3 4,5 5,5  12,25 (4,0đ) 3 3
Đặt y = x 5, phương trình trở thành  y  0,5   y  0,5  12,25 0,25 3 2 2 3 3 2 2 3  y 3.y .0,5 3. .
y 0,5  0,5  y  3.y .0,5 3. . y 0,5  0,5 12,25 0,25 2 3y  0,2512,25  0 0,25
1)  3 y  2 y  2  0 (2,0đ)  y  2 0,5    y  2
Với y = 2 , ta được : x = 7 0,5
Với y =  2 , ta được x = 3
Vậy nghiệm của phương trình là : x= 3 ; x= 7. 0,25 6 12 7   6 12 7 3   1 1 1  0 0,5 2 2 2 x  2 x  8 x  3 2 2 2 x  2 x  8 x  3 2 2 2 4  x 4  x 4  x     0 2 2 2 x  2 x  8 x  3 0,5    1 1 1  2 4  x     0   (1) 2) 2 2 2  x  2 x  8 x  3  (2 đ) 1 1 1 Có  
 0 với mọi giá trị của x. 2 2 2 x  2 x  8 x  3 0,25 x  2 Nên (1) 2
 4  x  0  x  2x  2  0   0,5 x  2 
Vậy phương trình có hai nghiệm : x = 2 ; x = 2. 0,25 4. a b   2 2 2 a b (2,0 đ)
C/m: Với x, y là số dương và a, b là số bất kì. Ta có   0,5 x y x  y
Áp dụng kết quả trên, ta có: 0,5 2  1 1  1 1  1    2 2  4 4    2x  y  x x  y  x  z x  y x  z 2 2 2 2 2 2 1 1  1 1   1 1   1   1   1   1                4 4  4 4   4 4   4   4   4   4         x  y x  z x  y x  z x y x z 1 1  2 1 1       
2x  y  x 16  x y z  1 1  1 2 1  1 1  1 1 2  Tương tự cũng có:    ;        0,25
x  2 y  z 16  x y z 
x  y  2z 16  x y z  1 1 1 1  2 1 1 1 1 2 1 2 1     
          2x  y  x x  2 y  z
x  y  2z 16  x y z x y z x y z  0,5 1 1 1 1  4 4 4  1  1 1 1               2x  y  x x  2 y  z
x  y  2z 16  x y z  4  x y z  1 1 1 1 1 1 Theo bài ra    4     1 (đpcm) 0,25 x y z 2x  y  x x  2y  z x  y  2z 5. E (5,0đ) D A M B I C
- Chứng minh  EBD ~  ECA (gg) 0,75 EB ED 1)   ( hai cạnh tương ứng) 0,5 (2,5đ) EC EA
Chứng minh:  EAD ~  ECB (c.g.c) 0,75  E  DA  E
 BC ( hai góc tương ứng) 0,5 Kẻ MI  BC. 0,75
Chứng minh  BMI ~  BCD (g.g) 2) BM BI  
( hai cạnh tương ứng)  BM.BD  BC.BI 0,5 BC BD
(2,5đ) Tương tự có CM.AC  BC.IC 0,5
Cộng vế với vế, ta được BM.BD  CM.CA  BC.BI  BC.CI  BC BI  IC  BC2 0,75
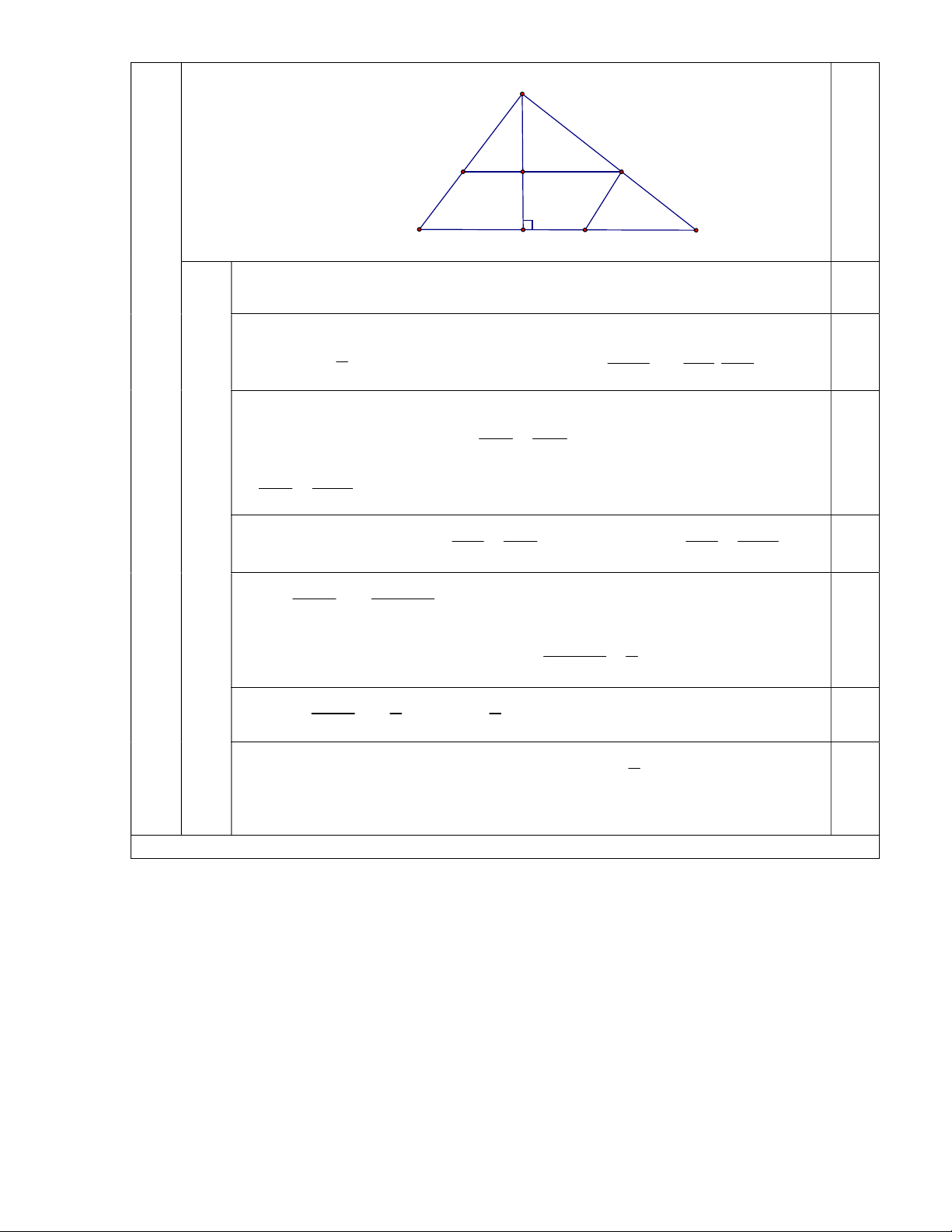
Mà BC không đổi => đpcm 6. A (2,0đ) F M G B C H E
Ta có ME // AB (gt) và MF // BC (gt)  ME // BF và MF // BE
 Tứ giác BEMF là hình bình hành ( hai cặp cạnh đối song song) 0,25
Kẻ AH  BC tại H , AH cắt MF tại G. 1 Ta có S  AH.BC và S  H . G FM nên S HG FM BEMF  2. . 0,25 ABC 2 BEMF S AH BC ABC
Gọi AM = x; MC = y  AC = x + y FM AM
Xét  ABC có MF // BC (gt)  
( hệ quả định lí Talet) BC AC 0,25 FM x   BC x  y HG CM HG y Xét  AHC có GM //HC   ( định lí Talet)   AH AC AH x  y 0,25 S xy Do đó BEMF  2. S x  y ABC  2 0,5 xy 1
Ta có :  x  y2  0   x  y2  4xy    x  y2 4 S 1 1 BEMF   2.  S  .S 0,25 S 4 BEMF 2 ABC ABC 1 Mà S không đổi nên S
đạt giá trị lớn nhất là .S khi và chỉ khi x = ABC BEMF 2 ABC 0,25 y
Hay M là trung điểm của AC.