PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 8 THIỆU HÓA NĂM HỌC 2021-2022 MÔN THI: TOÁN ĐỀ THI CHÍNH THỨC Ngày thi: 28/3/2022
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi có 05 câu, 01 trang)
Câu 1. (4,0 điểm): Cho biểu thức  a 2 2  3 4 2 1 M = 1 2a  4a 1
a  4a a 8a  4a 16     : 
3a a  2 3 2 2 1 a 1 a 1 4a a  4  
1. Rút gọn M. Tìm a để M < 5a.
2. Cho a, b, c đôi một khác nhau và khác 0. Cho a + b + c = 0
Tính N =  a  b b  c c  a   c a b    .   1      c a
b   a  b b  c c  a 
Câu 2. (4,0 điểm): 3 2
1. Giải các phương trình: 3 x 3 x   x  28  0 (x  ) 1 3 x 1
2. Tìm hai số x; y thỏa mãn 2 điều kiện sau: 3 2
x  xy 10y  0 và 2 2
x  6y  10
Câu 3. (4,0 điểm):
1. Tìm số x, y nguyên thỏa mãn: 2 2 3 2 2 2 2
x y  3xy  x  3xy  x y  3xy  6 y  6 y  7  0
2. Tìm tất cả các số chính phương gồm 4 chữ số biết rằng khi ta thêm 1 đơn vị vào
chữ số hàng nghìn , thêm 3 đơn vị vào chữ số hàng trăm, thêm 5 đơn vị vào chữ số hàng
chục, thêm 3 đơn vị vào chữ số hàng đơn vị , ta vẫn được một số chính phương.
Câu 4. (6,0 điểm)
Cho đoạn thẳng AB cố định có O là trung điểm. Trên đường thẳng vuông góc với
AB tại A, lấy điểm C sao cho AC  AO . Kẻ AK vuông góc CO tại K, điểm D đối xứng với
A qua K. Đường thẳng qua O vuông góc với AB cắt BD tại E. Kẻ DH vuông góc với AB tại H, DH cắt BC tại I. a. Chứng minh: CD = EO
b. Chứng minh: KI đi qua trung điểm của BD.
c.Kẻ IN vuông góc với AC tại N, kẻ DM vuông góc với AC tại M, DM cắt CO tại J.
Chứng minh tứ giác JNOI là hình bình hành. Khi C di chuyển (sao cho AC  AO ), Tính giá trị nhỏ nhất của 2 2 NI  OJ
Câu 5. (2,0 điểm): Cho a, ,
b c  0 thỏa mãn a  b  c  3   
Tìm giá trị nhỏ nhất của A = a 1 b 1 c 1   2 2 2
b 1 c 1 a 1
....................................................... HẾT................................................................
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm. HƯỚNG DẪN CHẤM CÂU ĐÁP ÁN ĐIỂM Câu 1.
(4,0 điểm) Ý 1 (2.5đ)
Điều kiện: a  0;a  1  a 2 2  3 4 2 1 1 2a  4a 1
a  4a a 8a  4a 16 * Ta có:     :  2 3 2 2     3a a  1 a 1 a 1 4a a  4   4 2 4a
a  8a  4a 16 M =  2 2   a 4 a 4   1.5
Vậy với a 0; a 1 Thì M = a2+4
* khi M < 5a Ta có a2+4 < 5a
 a2- 5a+4<0  (a-1)(a-4) <0  1 1.0 Ý 2. (1.5đ) Đặt a b b  c c  a c 1 a 1 b 1  ; x  ; y  z   ;  ;  c a b a  b x b  c y c  a z   Ta có 1 1 1
 N  (x  y  z)   1    x y z   
 y  z x  z x  y  N= 1 1 1
(x  y  z)   1  4         x y z   x y z  0.5 2 2         Ta lại có: y z b c c a c b bc ac a c   .  .   x  a
b  a  b ab a  b
c(a  b)(c  a  b)
c(c  a  b)
c c  a  b  c  2 2 ( ) 2c    
ab(a  b) ab ab ab 2 2
Tương tự ta có x  z 2a x  y 2b  ;  y bc z ac 2 2 2  1 1 1  2c 2a 2b 2 3 3 3
N  (x  y  z)   1  4     4 
(a  b  c )   0.5  x y z  ab bc ac abc Vì 3 3 3        a b c 0 a b c 3abc   Do đó N= 1 1 1 2
(x  y  z)   1  4 
.3abc  4  6  10    x y z  abc Vậy N= 10 0.5 Ý 1. (2đ) ĐK : x  1 Câu 2 3 2 Ta có x x 3 3 x    28  0 (4,0 điểm) (x  ) 1 3 x 1 x 0.5 3 x x 3 2 x (x  )  3 . x (x  )   28  0 x 1 x 1 x 1 x 1 2 2 x 3 x 2 3 2 x  ( )  ( 3 )  1 27  0 x 1 x 1 x 1 2 x 0.5  3 3 (  ) 1  3 x 1 2  x   1 3 x 1 2 x 0.5   4 x 1
 x2 - 4x + 4 =0  (x-2)2 = 0.  x=2 (TM) 0.5
Vậy phương trình đã cho có nghiệm x=2 Ý 2(2điểm)
Từ 10 = x2 +6y2 .Thay vào x3 +xy2 -10y =0 ta có 3 2
x  xy   2 2 x  6y  3 2 2 3
y  0  x  xy  x y  6y  0 0.5 3 2 2 2 2 3
 x  2x y  x y  2xy  3xy  6y  0  x  2y 2 2
x  xy  3y   0  x  2y x  y 2 2 2
x  xy  3y   0   2 2
x  xy  3y  0 0.5 2 2  y  y + Trường hợp 1: 2 2 11
x  xy  3y  0  x  
 0  x  y  0    2  4
Với x  y  0 không thỏa mãn phương trình (2).
+ Trường hợp 2: x  2y thay vào phương trình (2) ta có: 0.5
 y  1 x  2 2 2 2
4y  8y  12  y  1  
 y  1 x  2  0.5
Vậy  x; y   2; 1; 2  ;  1 . Ý 1. (2đ) Câu 3 Từ 2 2 3 2 2 2 2
x y  3xy  x  3xy  x y  3xy  6y  6y  7  0 (4,0 điểm
 (x2-3xy+6)(y2-y -1) =1=1.1=(-1)(-1) 0,5
TH1: x2-3xy+6 =1(1) và y2-y -1=1 (2)
Giải (2) ta có y2-y -2 =0  y=2 hoặc y=1
- Nếu y=2 Thay vào (1) ta được x2- 6x+5=0  x=1 hoặc x=5 0.5
- Nếu y=1 Thay vào (1) ta được x2- 3x+5=0 vô nghiệm 0.5
TH2: x2-3xy+6 =-1(1) và y2-y -1=-1 (2)
Giải (2) ta có y2-y =0  y=0 hoặc y=1
- Nếu y=0 Thay vào (1) ta được x2+7=0 vô nghiệm
- Nếu y=1 Thay vào (1) ta được x2- 3x+7=0 vô nghiệm 0.5
Vậy phương trình có nghiệm nguyên (x;y) là: (1;2); (5;2) Ý 2(2đ)
Gọi abcd là số phải tìm (a, b, c, dN, 0  a,b, c, d  , 9 a  0 ) Ta có: 2 abcd k với k, mN, 2 a (  b )( 1  c )( 3  d )( 5  ) 3  m 0.5 31  k  m  100 2 abcd k  2 abcd1353 m Do đó: m2–k2 = 1353 0.5
 (m+k)(m–k) = 123.11= 41. 33 ( k+m < 200 ) m+k = 123 m+k = 41  m –k = 11 m hoặc –k = 33 m = 67 m = 37 0.5  k =56 k hoặc = 4
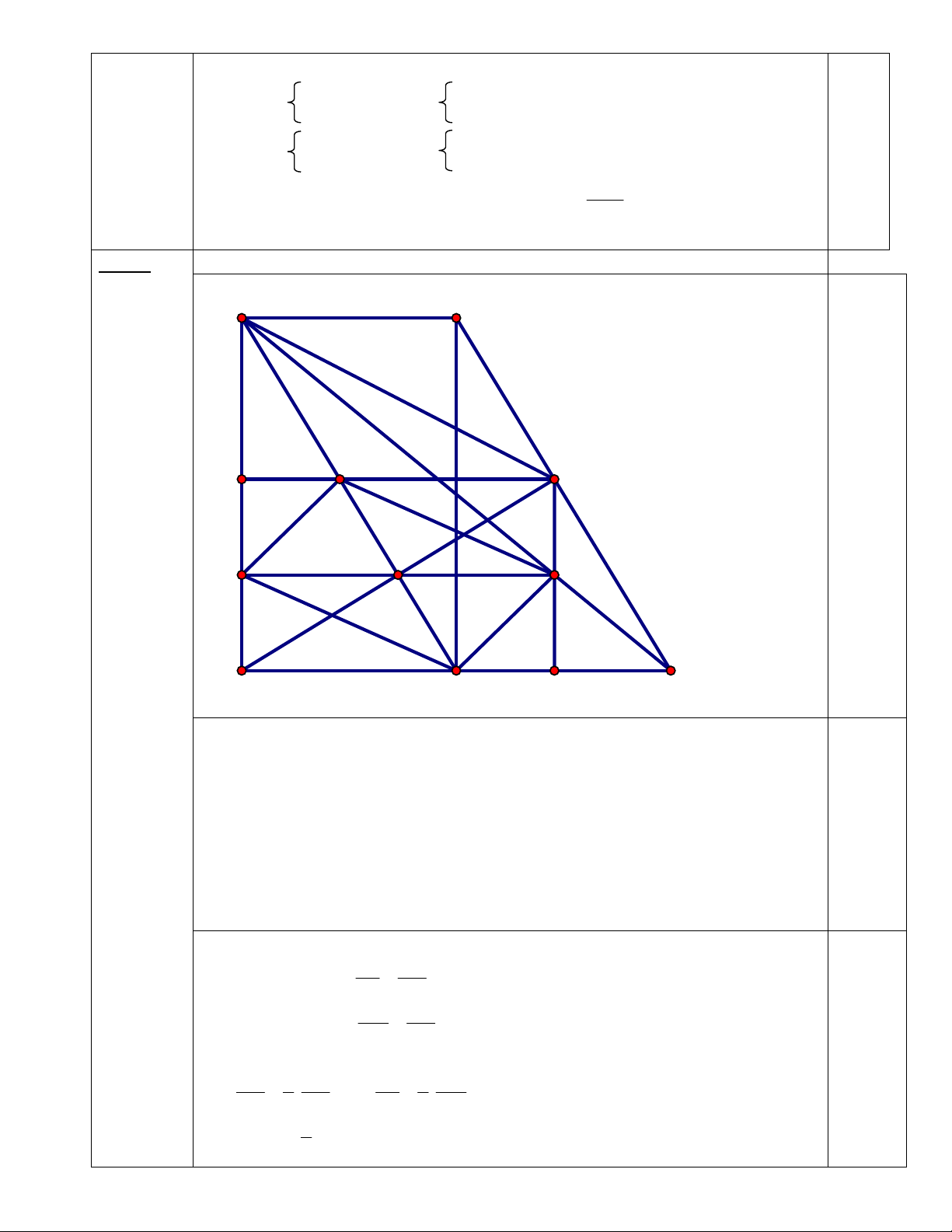
Kết luận đúng abcd =3136 0.5 Câu 4 (6,0 điểm) C E J M D I N K A O H B a.(2d)
Chứng minh được CO // BE ( cùng vuông góc với AD) 0.5
Chứng minh được : ACO  OEB (cạnh huyền – góc nhọn) nên AC = OE. 1,0
Mà AC = CD(CO là trung trực của AD). Suy ra CD = EO. 0.5 b.(2d) Do IH // AC nên IH BH  0.5 CA BA Do DH // EO nên: DH BH  0.5 EO BO Mà BH 1 BH  IH DH . nên 1  . . Mà CA = EO 0.5 BA 2 BO CA 2 EO Suy ra 1
IH  DH hay I là trung điểm DH, mà K là trung điểm của AD nên 2 0.5
IK// AB suy ra IK đi qua trung điểm của BD. c.(2d)
Do AMDH là hình chữ nhật và có I là trung điểm DH và IN vuông góc 0.5
MA nên N là trung điểm AM và K là trung điểm AD nên I, K, N thẳng hàng. 0.25
Chứng minh JKD  OKA  KJ  KO
Chứng minh NKA  IKD  KN  KI 0.25
Suy ra tứ giác NJIO là hình bình hành
Chứng minh được NI = AH, JO = BD 0.25 Ta có 2 2 2 2
NI  JO  AH  BD 0.25 Chứng minh được 2
BD  BH.AB nên : 2 2 2 2
NI  JO  AH  BH.AB  AH   AB  AH  2 2
.AB  AH  A . B AH  AB 2  1  3 3 2 2
 AH  AB  AB  AB    2  4 4 Vậy GTNN của 3 2 2 NI  JO là 2 AB khi 1 AH  AB 0.5 4 2 Câu 5
(2,0 điểm) Sử dụng bất đẳng thức Cô si 2 a 1 b a   2 1 b a   Ta có: 1 b  ab  a 1  a 1  a 1 (1) 2 2 b 1 b 1 2b 2 Tương tự: b 1 c  bc    c 1 a ca b 1 (2) và  c 1 (3) 2 c 1 2 2 a 1 2 1.0
Từ (1); (2) và (3) suy ra: a 1 b 1 c 1
a  b  c
ab  bc  ca     3  2 2 2
b 1 c 1 a 1 2 2 Mặt khác 2 2 2
a  b  c  ab  bc  ca hay ab  bc  ca  a  b  c2 3( )  9 0.5 Do đó: a 1 b 1 c 1
a  b  c
ab  bc  ca     3  = 3 9  3  2 2 2
b 1 c 1 a 1 2 2 2 6 Vậy A= a 1 b 1 c 1    3 . 2 2 2
b 1 c 1 a 1 0.5
GTNN A= 3 Dấu bằng xảy ra khi a = b = c = 1