UBND HUYỆN YÊN ĐỊNH
KÌ THI HỌC SINH GIỎI LỚP 8,
PHÒNG GIÁO DỤC&ĐÀO TẠO
CHỌN ĐỘI TUYỂN VÒNG 1 DỰ THI
HỌC SINH GIỎI LỚP 9 CẤP TỈNH ĐỀ
NĂM HỌC: 2024 - 2025 CHÍNH THỨC Môn thi: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang; gồm 05 câu) Câu 1 (4,0 điểm).  x 5  x  2x  5 2x 5
1. Cho biểu thức: P   :   
với x  0; x  5  ; x  2 2 2
 x  25 x  5x  2x 10x 5  x 2 Rút gọn biểu thức P.
2. Cho ba số a, b, c khác 0 và thỏa mãn: a + b + c = 0. Tính giá trị của biểu thức: 1 1 1 P    . 2 2 2 2 2 2 2 2 2
a  b  c
b  c  a c  a  b Câu 2 (4,0 điểm).
1. Giải phương trình:  x  2 4
5 2x  3 x   1  9 2. Cho , a ,
b c là các số thực đôi một khác nhau thỏa mãn 3 3 3
a 1  3a; b 1  3 ; b c 1  3 . c Chứng minh: a) a + b + c = 0 b) a2 + b2 + c2 = 6 Câu 3 (4,0 điểm).
1. Tìm tất cả các số x, y nguyên thỏa mãn: x4 + y + 4 = y2 – x2
2. Tìm tất cả các số nguyên tố p có dạng 2 2 2
p  a  b  c , trong đó a, b, c là các số nguyên dương thỏa mãn 4 4 4
a  b  c chia hết cho p.
Câu 4 (6,0 điểm). Cho hình vuông ABCD có cạnh là a. Điểm E thuộc cạnh BC, F là giao
điểm của AE và DC, G là giao điểm của DE và BF. Trên tia đối của tia DC lấy điểm M sao
cho BE = DM. Gọi T là trung điểm của EM.
1. Chứng minh tam giác AEM vuông cân và ba điểm B, T, D thẳng hàng.
2. Gọi I, K theo thứ tự là giao điểm của AB với CG và DG. Chứng minh IE song song với BD.
3. Tìm vị trí điểm E trên cạnh BC để tổng BK+CF đạt GTNN
Câu 5 (2,0 điểm). Cho hai số thực dương x, y thoả mãn: x + y + xy = 3 1 1 1
Tìm giá trị nhỏ nhất của biểu thức P = + + 𝑥+𝑦 𝑥 𝑦 ____HẾT____ HƯỚNG DẪN CHẤM Câu Nội dung Điểm 5
1. Với x  0; x  5  ; x  ta có: 2  x x  5  2x  5 2x 0,5 P     
x   x  
x  x   : 5 5 5 2x 
x 5 5 x
x   x  2 2 5 2x  5 2x  
x  x   x   : 5 5
2x  x  5 5  x 
x  x  5 x  x  5 2x  x  5 2x   0,5
x  x   x   . 5 5 2x  5 5  x 5.2x  5
2x  x  5 2x Câu  
x  x   x   . 5 5 2x  5 5  x 1 10 2x   0,5 x  5 x  5 10  2x 25  x    2  x  5 x  5 0,5 5 Vậy P  2
 với x  0; x  5  ; x  2 1,0
2. Từ a  b  c 
 a  b  c
  a  b2   c  2 2 2 2 0
 a  b  c  2  ab 0,5 Tương tự: 2 2 2
b  c  a  2  bc ; 2 2 2
c  a  b  2  ca   Do đó: 1 1 1 c a b 0,5 P       0 2  ab 2  bc 2  ca 2abc 1.  x  2 4
5 2x  3 x   1  9   2
16x  40x  25 2
2x  5x  3  9  8   2
2x  5x  25  2
 2x 5x  3   9 0,75 Đặt 2
2x  5x  t
 8t  25t 3  9 2
 8t  49t  66  0 Câu
 t  28t 33  0 2 0,5  33
t  2 hoặc t   8 1 +) 2 t  2
  2x 5x  2
  x  2 hoặc x  2 33 33 33 +) 2 2 t  
 2x 5x  
 2x  5x   0 8 8 8 2 33  5  2
 4x 10x   0  2x   2  0  
(vô nghiệm vì (2x-5/2)2 + 2 > 0 với 0,5 4  2  mọi x) Câu Nội dung Điểm 1  0,25 Vậy S   ;2 2  2. a) Từ giả thiết: 3 3 3
a 1  3a;b 1  3 ;
b c 1  3c ta có: 3 3
a b  3a b 2 2
a  ab  b  3 (1)    3 3 b
  c  3b  c 2 2  b
  bc  c  3 (2) 0,5  
(vì a, b, c đôi một khác nhau) c   a  3  c a 2 2 3 3
c  ca  a  3 (3)  Từ (1) và (2) suy ra: Câu 2 2
a  c  ab  bc  0  a  ca  b  c  0  a  b  c  0 . 0,5 2
(vì a, b, c đôi một khác nhau)
b) Cộng (1); (2); (3) vế với vế ta có: 2 2 2
2a  2b  2c  ab  bc  ca  9 0,5
 a  b  c   b  bc  ca   a  b  c  a  b  c2 2 2 2 2 2 2 4 2a 2 2 18 3 18 .   2 2 2
3. a  b  c   0 18 . a2 + b2 + c2 = 6 0,5 1 1
1. Ta có x4 + y + 4 = y2 - x2  (x2 + )2 - (y - )2 = -4 2 2 0,5
 (x2 + y)(x2 – y + 1) = -4
Ta có x, y nguyên; (x2 + y + x2 – y + 1) = 2x2 + 1 là số lẻ
nên x2 + y và (x2 – y + 1) phải có một số là số lẻ 0,25 Ta có bảng: x2-y+1 -1 - 4 4 1 x2+y 4 1 -1 -4 0,75 y 3 3 -2 -2 x2 1 -2 (loại) 1 -2 (loại) x 1; -1 1; -1 Câu
Vậy các số nguyên (x,y) cần tìm là: (1;3); (-1;3); (1;-2); (-1;-2). 0,5 3
2. Không mất tính tổng quát, ta có thể giả sử : a  b  c 1.. 2 - Ta có : 4 4 4
a  b  c   2 2 2
a  b  c    2 2 2 2 2 2
2 a b  b c  c a . 0,5
- Vì p là số nguyên tố và 2 2 2
p  a  b  c , với a  b  c 1 nên p  3 . Suy ra 4 4 4
a  b  c chia hết cho p khi và chỉ khi 2 2 2 2 2 2
a b  b c  c a chia hết cho p 0,5 hay 2 2 2 a b  c  2 2 b  a  2 2 4
p  a b  c p   2 ab  c  2 ab  c  . p - Vì 2 2 2 2 2
p  a  b  c  ab  c  ab  c  0 và p là số nguyên tố nên 0,5 2
ab  c  0 . 2
 ab  c  a  b  c ( vì a  b  c ) 2
 p  3a  a  b  c  1 và p = 3.
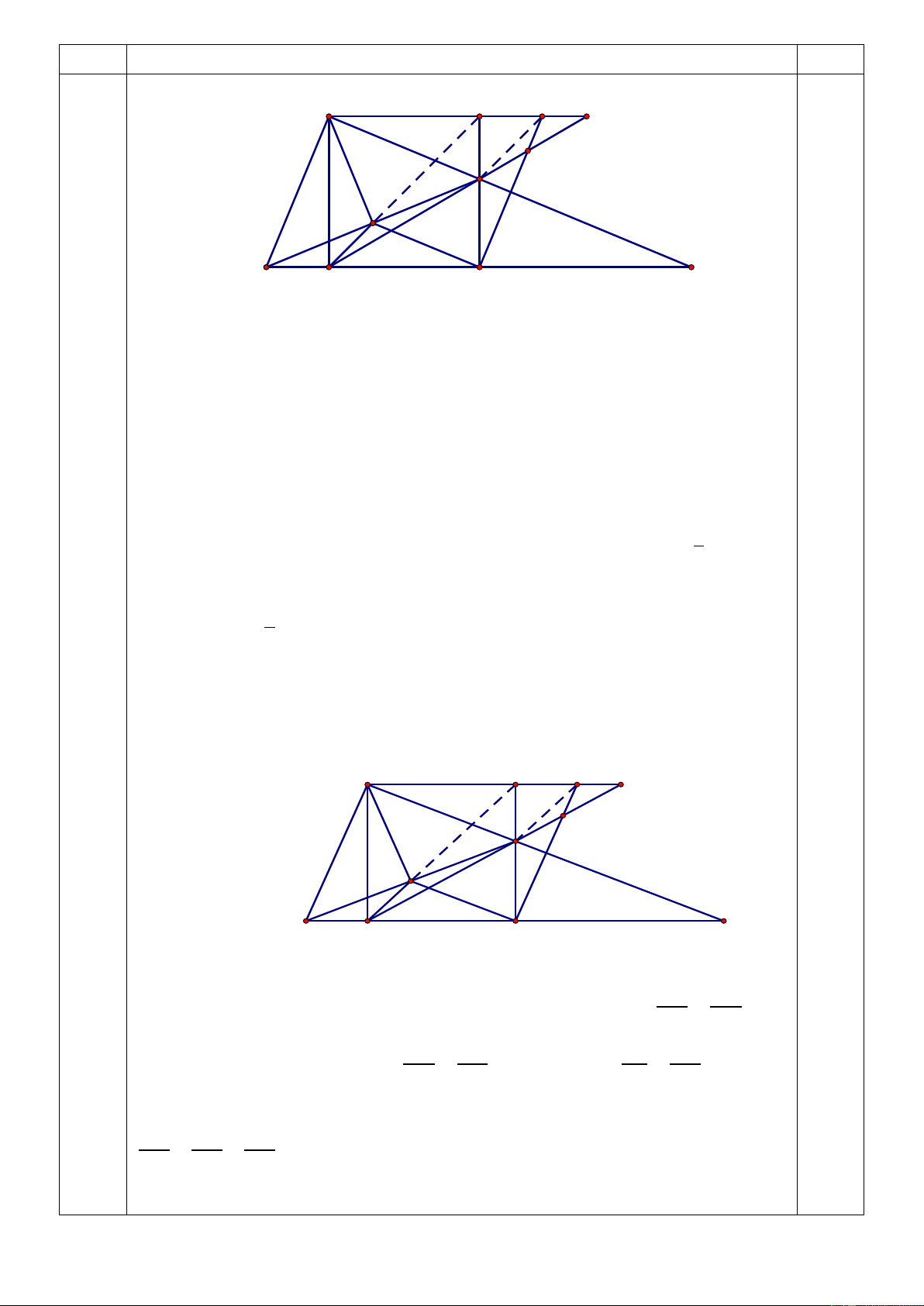
Vậy có duy nhất một số nguyên tố thỏa mãn là p = 3. 0,5 Câu Nội dung Điểm A B I K G E T M F D C 1.(2,5 điểm) Xét A  DM và ABE  có : 0
AD  AB  a, ADM  ABE  90 , MD  BE ( gt). Suy ra : A  DM  A  BE ( .
c g.c) .  AM  AE ( các cạnh tương ứng) (1) 0,75
Và  DAM  BAE ( các góc tương ứng ) Mà 0
DAE  BAE  DAB  90 0,75 0 0
 MAD  DAE  90  MAE  90 (2)
Từ (1) và (2) suy ra A
 ME vuông cân tại A Ta có A
 ME vuông cân tại A, T là trung điểm của ME nên 1 AT  ME (trung 2
tuyến ứng với cạnh huyền) 0,5 Câu Tương tự 1 CT  ME 2 4
Suy ra: TA = TC. Mà BA = BC, DA = DC ( cạnh của hình vuông) nên 3 0,5
điểm T, B, D cùng nằm trên đường trung trực của AC. Suy ra B, T, D thẳng hàng 2) (2,0 điểm) A B I K G E T M F D C
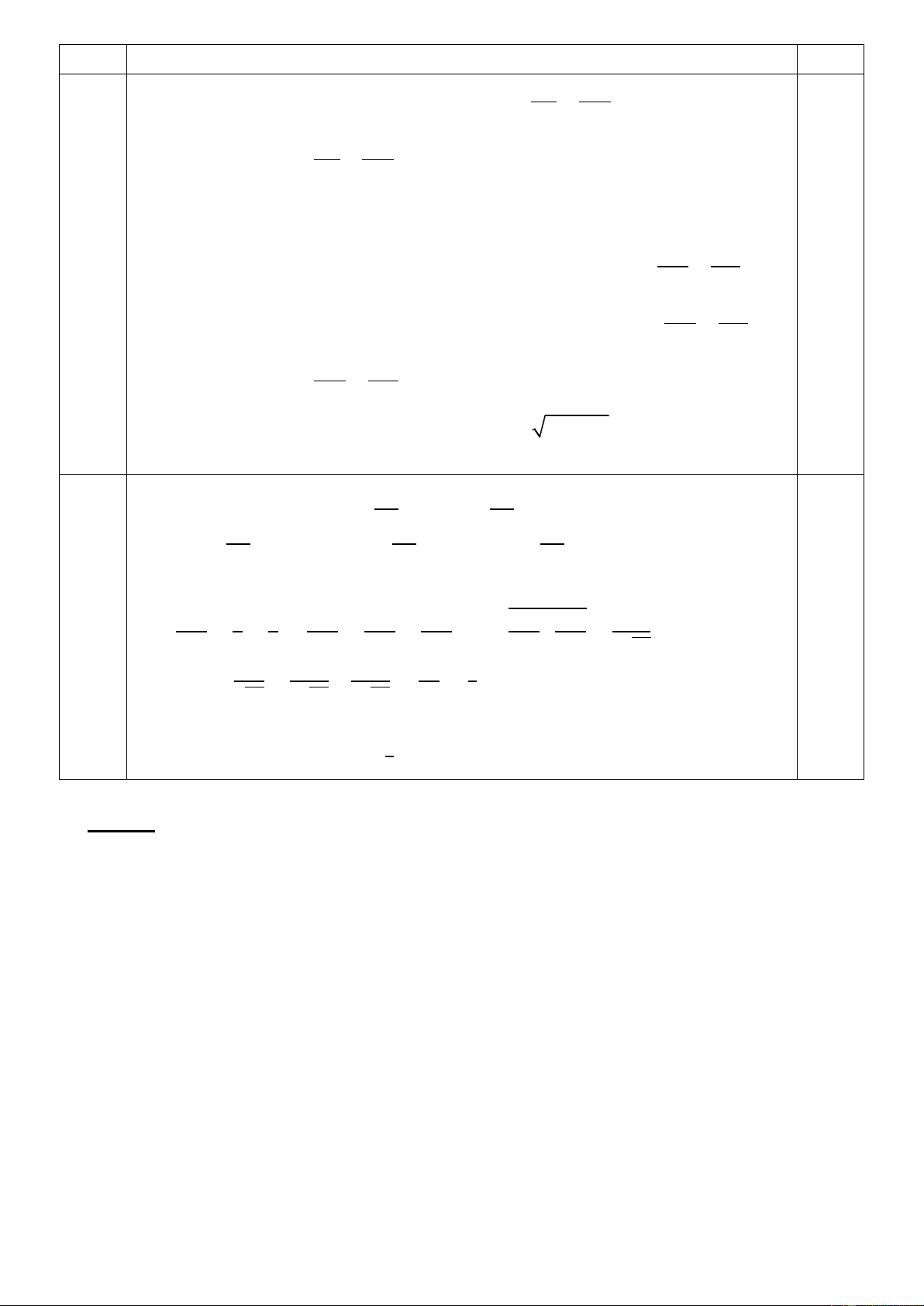
Vì ABCD là hình vuông nên AB//CD => BK//DF và AK//DF IK IG
Xét tam giác DCG có IK//CF nên theo định lí Thales ta có:  CD GC IG IB IK CD
Chứng minh tương tự ta được:  . Từ đó suy ra   1 0,5 GC CF IB CF
Xét các tam giác EDC và ECF có AK//DF, theo định lí Thales ta có: KE BE AB   2 0,5 ED EC CF Câu Nội dung Điểm IK KE 0,5
Ta lại có AB = CD nên từ (1) và (2) suy ra:  IB ED IK KE 0,5 Tam giác BKD có: 
nên IE//BD (Theo định lí Thales đảo). IB ED 3.(1,5 điểm) AB BE
Xét tam giác CEF có AB//CF nên theo định lí Thales ta có: 0,25  3 CF CE BK BE
Xét tam giác DEC có BK//CD nên theo định lí Thales ta có: 0,25  4 CD CE
Từ (3) và (4) suy ra BK AB 2 
 BK.CF  A . B CD  a 0,5 CD CF Do 2
BK.CF  a không đổi nên BK  CF  2 BK.CF  2a đạt giá trị nhỏ 0,5
nhất khi và chỉ khi BK  CF  a Khi đó E là trung điểm của BC.
Áp dụng bất đẳng thức CAUCHY ta có:
3 = x + y + xy ≥ 2√𝑥𝑦 + xy = (√𝑥𝑦 + 1)2 – 1 0,5 0,25
=>4 ≥ (√𝑥𝑦 + 1)2 => 2 ≥ √𝑥𝑦 + 1 => 1 ≥ √𝑥𝑦 (do x, y>0)
Câu Áp dụng bất đẳng thức CAUCHY ta có: 5 1 1 1 4 𝑥+𝑦 3 4 𝑥+𝑦 3 P = + + = + − ≥ 2√ ⋅ − 0,5 𝑥+𝑦 𝑥 𝑦 𝑥+𝑦 𝑥𝑦 𝑥+𝑦 𝑥+𝑦 𝑥𝑦 2 √𝑥𝑦 4 3 5 5 5 = − = ≥ = √𝑥𝑦 2√𝑥𝑦 2√𝑥𝑦 2.1 2 0,25
Đẳng thức xảy ra  x = y = 1 0,25 5
Vậy giá trị nhỏ nhất của P = khi x = y = 1. 0,25 2
Lưu ý: +) Câu 4.2; 4.3 hình học các em học sinh có thể sử dụng tam giác đồng dạng
để biến đổi ra các tỉ số.
+) Học sinh làm cách khác đáp án mà đúng thì vẫn cho điểm tối đa.
+) Câu 1.1 học sinh có thể không ghi điều kiện xác định trong kết luận vẫn cho điểm tối đa.