Đề thi hsg môn toán 12 tỉnh quảng trị năm 2018 có đáp án

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 12 THPT QUẢNG TRỊ
Khóa ngày 02 tháng 10 năm 2018 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 180 phút, không kể thời gian giao đề
Câu 1. (3,0 điểm)Cho hàm số y  x3  mx2 3  ( 3 2m  ) 3 x  .
1 Tìm tất cả các giá trị của tham  1 1 
số m để hàm số nghịch biến trong khoảng  ; .    2 2 
Câu 2. (4,0 điểm)
1.Giải phương trình:  x   x2 19 3 2 4
 4x  24  6 2  x 12 3  x .
x3  y3  3x2 6x 3y  4
2.Giải hệ phương trình: 
x2  y2  4x 2y  8  5x  6  4x  3y 14   0
Câu 3. (2,0 điểm) Cho a, b, c là các số thực dương thỏa mãn a  b  c  . 1 Tìm giá trị nhỏ nhất của biểu thức a2 b2 3 2 P    2 2 a b
bc  b 5 c c  a .  c 5 a 4
Câu 4. (2,0 điểm) Bạn An vẽ lên giấy một đa giác lồi  H  có số cạnh nhiều hơn 4. Sau đó
bạn An đếm các tam giác nhận đỉnh của đa giác làm đỉnh và nhận xét: số tam giác không
có cạnh chung với  H  nhiều gấp 5 lần số tam giác có đúng một cạnh chung với  H . Hỏi
bạn An vẽ đa giác lồi có bao nhiêu cạnh?
Câu 5. (6,0 điểm)  3 
1.Trong mặt phẳng tọa độ (Oxy), cho tam giác ABC  AC  AB. Gọi D ; 2    là  2 
chân đường phân giác trong góc , A E  ,
1 0 là một điểm thuộc đoạn AC thỏa mãn AB  A .
E Tìm tọa độ các đỉnh ,
A B, C biết phương trình đường tròn ngoại tiếp tam giác
ABC là x2  y2  x  2 y  30  0 và A có hoành độ dương.
2.Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại  , A ABC  0 60 , BC  a 2 . Gọi
H là hình chiếu vuông góc của A trên .
BC Biết SH vuông góc với mặt phẳng  ABC  và
SA tạo với mặt phẳng SBC  một góc . 0
30 Tính thể tích khối chóp S.ABC và tính khoảng
cách từ B đến mặt phẳng SAC  theo a.
Câu 6. (3,0 điểm) Cho dãy số (x ) biết n x  a  1  3 1 x
 x2  x3 ( n    , n  )  1 n1 n n  4 8
1.Với a  3 , chứng minh rằng dãy (x ) có giới hạn hữu hạn và tìm giới hạn đó. n
2. Chứng minh rằng với mọi a [-2; ]
6 , dãy (x ) có giới hạn hữu hạn. n
--------- HẾT---------
(Thí sinh không được sử dụng tài liệu và máy tính cầm tay) Trang1 HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 12 THPT NĂM HỌC 2018 - 2019 Môn thi: TOÁN Câu Ý Nội dung Điểm
Ta có y '  x2 3  6mx  ( 3 2m  ) 3 0,5  1 1   1 1 
Hàm số nghịch biến trong khoảng  ;  y '  , 0 x    ;     0,5  2 2   2 2  x2 3 1 1 2     0,5 2m(x  )
1  x  3  m  , x    ; .   2x  2  2 2  1 x2  3  1 1  (3,0đ)
Xét hàm số f (x)  trên khoảng  ;   0,5 2x  2  2 2  (x  ) 1 (2x  ) 6  1 1 
Ta có f '(x)   0     2   2x  2 , x ;  2 2  0,5
Từ bảng biến thiên suy ra m   13 . 0,5 4
Giải: Điều kiện: 3  x  . 2
Phương trình đã cho tương đương với
19  3x  4 2  x3  x  6 2  x 2 3  x  0,5
Đặt t  2  x  2 3  x ta có t2  14  3x  4 2  x3  x , t   1 Phương trình trở thành: 0,5 t2  t 6  5  0   t   5
Với t  1 ta có 2  x  2 3  x  1  3x 13  4 2  x3  x  0
Phương trình vô nghiệm do 3  x  . 2 0,5 1
(1,0đ) Với t  5 ta có
2  x  2 3  x  5  2  x  4 3  x  4 2  x3  x  25  11 x  2 
 4 x  x  6  11 3x   3 2  2 (
16 x2  x  ) 6   113x (4,0đ)  11 x    3
 x  1tmđk  
25x2  50x  25  0
Vậy phương trình có nghiệm x  . 1 0,5
x3  y3  3x2  6x  3y   4   1 
x2  y2  4x 2y  8  5x  6  4x  3y 14   0 2  6    Điề x u kiện:  5 
4x  3y 14  0    3 y3 1
 3y  1 x  31 x ( ) 3 0,5  3  3   2 3  3  0  
Xét hàm số f (t) t t, t
R ta có f '(t) t t R , hàm
số f đồng biến trên R nên từ 3 ta có y  1 . x 0,5 Trang2
Thế vào 2 ta có phương trình: 2
2x  4x  9  5x  6  7 x  11  0 4 ( điều kiện x   6 ) 5  x2 2
2x  4  x2 5x6x3 7x11 2 (2,0đ) 2 2 x  2  5x  6 x  3  7x 11
 2x2  x 2          
x  2  5x  6
x  3  7 x  11 2  2 2 2 2 2   2 x  x  x  x   x x  
x  2  5x  6
x  3  7 x  11
x2  x 2  0   0,5  1  1  2*
 x 2  5x  6 x  3  7x 11
Với x   6 ta có 5 1  1  1  1  65  2
x  2  5x  6
x  3  7x 11  6  2  6  36 3 5 5 Do đó phương trình 
* vô nghiệm, phương trình 4 có hai nghiệm x   , 1 x  2.
Vậy hệ phương trình có hai nghiệm  ; 1 2;  ; 2   1 . 0,5 a2 a2 4a2    2 2 0,5
b  c  bc 5  2 5 2 9 
b  c  b  c b c . 4 b2 b2 4 Tương tự ta có   2 2
c  a  c 5 a 9c  a .  2 4 a2 b2  3 2 2  a b  3 2 P      0,5 2 2 a b      a b
9  b  c
c  a  4 9     b c c a  4 3 2  2
a2  b2  c a  b  3 (2,0đ)      2  9 ab c a b 2 a b c       4   2 2 a  b   
c a  b  2  2  3 8 2 3 2 1 1 2  2     2 a  b       c 9   0,5 a  b  4 9  1  4 
 ca  b c  c2   4  Xét 8  2 2 3 2 f (c)  1 
 1 c , c  
 ;01. f '(c)   c  1 0 . 9  c  1  4 3
Lập bảng biến thiên và từ đó suy ra 1 f (c)   , c   ; 0 1. 9
Ta có P  f (c)   1 dấu đẳng thức xảy ra khi a  b  c  1 . 9 3 Vậy 0,5 min P   1 . 9
Gọi n (n  4) là số cạnh của đa giác. 0,5 Trang3
Số tam giác có 3 đỉnh là đỉnh của đa giác C3 n
Số tam giác có 3 đỉnh là đỉnh của đa giác và có 1 cạnh chung với (H) là 0,5 n(n  4)
Số tam giác có 3 đỉnh là đỉnh của đa giác và có 2 cạnh chung với (H) là 4 n (2,0đ)
Số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh chung với 0,5 (H) là C3  ( n n  ) 4  n n
Theo giả thiết C3  ( n n  ) 4  n  5 ( n n  ) 4 . n
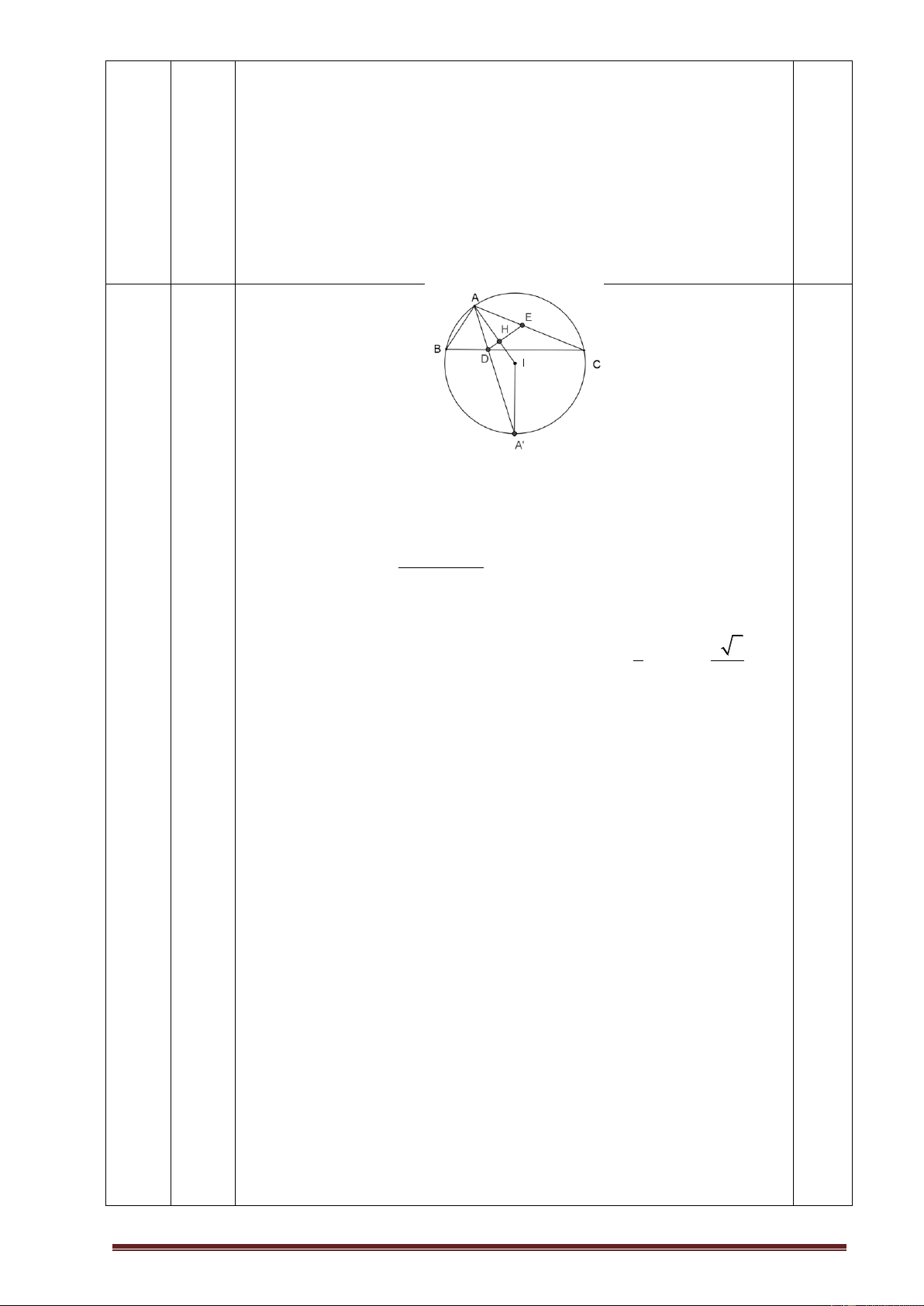
Giải phương trình này, ta được n  35 0,5   Gọi H AI D . E Ta có  
AB  AE, BAD  EAD và AD chung nên   A  BD  A
 ED  AED  ABC. 0  180  AIC Ta có   0  HAE  ICA   90  ABC. 2 Suy ra    0 
AED  HAE  ABC    ABC  0    AHE  . 0 90 90 90 1,0  1  Đườ 5 5
ng tròn ngoại tiếp tam giác ABC có tâm I  ;1 , R  .   1  2  2
(3,0đ) Phương trình đường thẳng AI : 2x  y  2  0 x  2  
2x  y  2  0 y  6
Tọa độ A là nghiệm của hệ:  
x2 y2 x 2y      30  0 x    3  y  4
Do A có hoành độ dương nên A ; 2 6. 0,5
Phương trình đường thẳng AD : x  2  0. Gọi
A ' là giao điểm thứ 2 của AD và đường tròn C  A' ; 2 4.
Phương trình đường thẳng BC : x  2y  5  0. 0,5 x  5  
x  2 y  5  0 y  0  
Tọa độ B, C là nghiệm của hệ
x2 y2 x 2y      30  0 x  3     y 4 B ; 5 0, C  ; 3 4 0,5 5 Suy ra  B   ; 3 4, C  ; 5 0 (6,0đ) 0,5
Do AC  AB nên B  ; 5 0, C  ; 3 4. Trang4 0 0 0,5
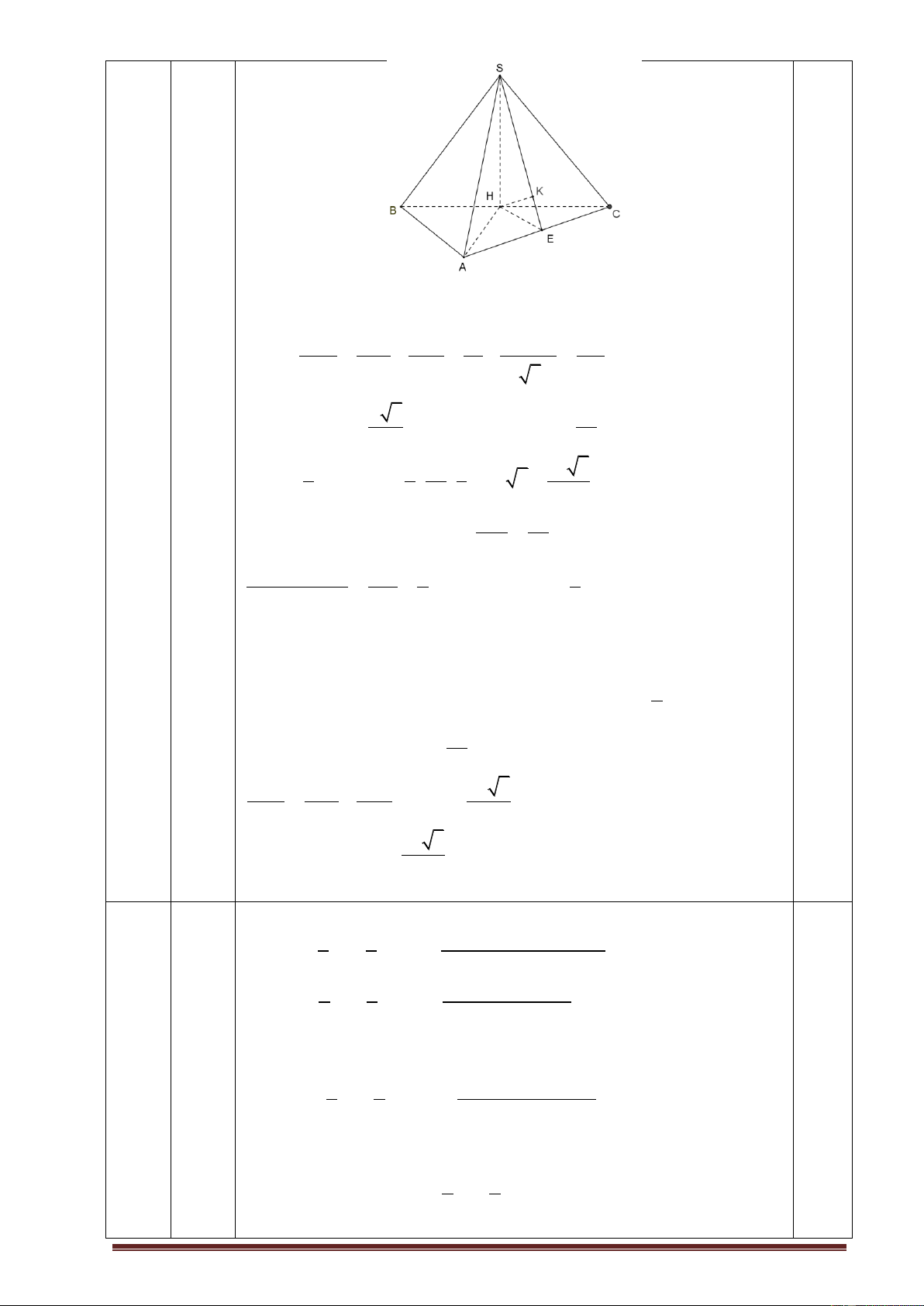
Góc giữa SA và mp SBC là  ASH  30 . suy ra  SAH  60 . 1  1  1  1  1  4 AH 2 AB2 AC2 a2  2 2 a 3  3a Ta có a 3 3 0,5 0 a  AH 
 SH  AH tan 60  . 2 2 3 1 1 3a 1 a 3 V  SH.S  
 aa 3  . 0,5 SABC A  BC 3 3 2 2 4 2 CA2 3 2 a
Ta có CA  CH.CB  CH   . (3,0đ) CB 2
d B,SAC  CB   4   4 d 
d B, SAC 
d H , SAC 
H , SAC      CH 3 3 0,5
Hạ HE  AC, HK  SE, ta có
AC  HE, AC  SH  AC  SHE  AC  HK mặt khác
HK  SE suy ra HK  (SAC). Vậy d  B,SAC   4 HK 3 3 0,5 0 a
Ta có HE  CH.sin 30  , và 4 1 1 1 a    3 5 HK  . HK2 HS2 HE2 10 a 0,5 Vậy d  ,
B SAC  2 5 . 5 Ta có 3 1 (x  ) 2 (x2 4 8 2 3  x  ) n n n 2    2   2   x x x 0 khi x 4 n1 n n 4 8 8 n 3 1 2 4 2 3
(x  )(x  )2 n n x
 4  x  x  4 
 0 khi 2  x  4 n1 n n 4 8 8 n
Do đó nếu 2  x  4 thì 2  x
 4 . Do 2  x  4 nên 2  x  4 1 n n1 1 n 0,5 (1,5đ) Ta lại có: 3 1 2 4 2 3    x (x )(x ) n n n x
 x  x  x  x   0  x  x n1 n n n n n1 n 0,5 4 8 8
Dãy (x ) tăng và bị chặn nên có giới hạn hữu hạn. n b  0 (l) Đặt 3 1 2 3  lim x  . b Ta có b  b 
b  b  2 (l) n  4 8 b   4 Trang5 Vậy lim x  4. n 6 0,5 (3đ)
Từ ý 1, ta có 2  a  4 thì dãy (x ) có giới hạn hữu hạn. n  a  0 Hiển nhiên với  
là dãy hằng nên có giới hạn hữu 2 a  2 thì dãy (x ) n 0,5 (1,5đ) a   4 hạn. Với 0,5
0  a  2 , dễ dàng chứng minh được 0  x  2 và dãy giảm nên có n giới hạn 0,5
Với 2  a  0hoặc 4  a  6 thì 0  x  4 nên (x ) có giới hạn hữu 2 n hạn
Vậy với mọi a [-2; ]
6 , dãy (x ) có giới hạn hữu hạn. n Trang6