Đề thi HSG Toán 11 cấp trường năm 2020 – 2021 trường Liễn Sơn – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 11 THPT CẤP TRƯỜNG TRƯỜNG THPT LIỄN SƠN NĂM HỌC 2020-2021 ĐỀ CHÍNH THỨC ĐỀ THI MÔN: TOÁN
(Dành cho học sinh THPT không chuyên)
Thời gian làm bài: 180 phút, không kể thời gian phát đề Câu 1 (4,0 điểm). cos x
a) Tìm m để hàm số y  có tập xác định là . 
3sin 5x  4cos5x  2m  3 2 3 cos x  cos x 1 b) Giải phương trình: 2 cos 2x  tan x  2 cos x
Câu 2 (2,0 điểm). Xung quanh bờ ao của gia đình bác Nam trồng 20 cây chuối. Do không còn phù hợp
bác muốn thay thế để trồng bưởi, lần đầu bác chặt ngẫu nhiên 4 cây. Tính xác suất để trong 4 cây bác
Nam chặt không có hai cây nào gần nhau.
Câu 3 (2,0 điểm). Cho n là số nguyên dương thỏa mãn n 1  n C  C
 4(n  2). Tìm hệ số của 5 x n4 n3
trong khai triển nhị thức Niu – tơn của n 2 2  (1 2 )  (1 3 ) n P x x x x .
Câu 4 (2,0 điểm). Cho dãy số u được xác định bởi: n  1 n 1 n  12n   1 2021nu * u  , u  u  ; n   . Tính lim n 1 n 1 3  n n n  2 1  2  2 n  2 2020   2 1  2 x  2 x  3x  1
Câu 5 (2,0 điểm). Giải bất phương trình  1. 2 1  2 x  x  1
Câu 6 (2,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có ( A 5  ;2) . M ( 1  ; 2  )
là điểm nằm bên trong hình bình hành sao cho  MDC  
MBC và MB  MC . Tìm tọa độ điểm D biết  1 tan DAM  . 2
Câu 7 (4,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a .  1 
Gọi M là điểm nằm trên SB sao cho SM  SB . 3
a. Gọi (P) là mặt phẳng chứa CM và song song với S .
A Tính theo a diện tích thiết diện tạo
bởi (P) và hình chóp S.ABC . D
b. E là một điểm thay đổi trên cạnh AC . Xác định vị trí điểm E để ME vuông góc với C . D
Câu 8 (2,0 điểm). Cho a, b, c là độ dài 3 cạnh của một tam giác có chu vi bẳng 1. Tìm giá trị lớn nhất 2 2 2 4 4 4 a  b  c 1 của biểu thức:T     . a  b b  c c  a 2abc -------------Hết-----------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………….………..…….…….….….; Số báo danh…………………… TRƯỜNG THPT LIỄN SƠN
KỲ THI CHỌN HSG LỚP 11 THPT CẤP TRƯỜNG NĂM HỌC 2020-2021 (Đáp án có 06 trang) ĐÁP ÁN MÔN: TOÁN 11
(Dành cho học sinh THPT không chuyên) I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm
theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học nếu thí sinh không vẽ hình phần nào thì không cho điểm tương ứng với phần đó. II. ĐÁP ÁN: Câu Nội dung trình bày Điểm 1 Câu 1 (4,0 điểm). cos x
a) Tìm m để hàm số y  có tập xác định là . 
3sin 5x  4cos5x  2m  3 2 3 cos x  cos x 1 b) Giải phương trình: 2 cos 2x  tan x  2 cos x 1a.(2,0 điểm)
Hàm số có tập xác định là  khi và chỉ khi
f (x)  3sin 5x  4cos5x  2m  3  0, x   .  0,5 3 4 2m  3 Ta có: f (x)  0, x
    sin5x  cos5x  , x   .  0,5 5 5 5  3 cos  2m 3  sin(5x     )  , x    với 5  0,5 5 4 s  in   5 2m  3
Do 1  sin(5x )  1, x
   nên f (x)  0, x      1  m  1. 5 0,5 Vậy m  1  . 1b.(2,0 điểm)  Điều kiện: x   l l  2 0,5 Suy ra 2 2
(1)  cos 2x  tan x  1 cos x  (1 tan x) cos x  1 2 cos 2x cos x 2cos x cos x 1 0          1  cos x  0,5  2 cos x  1
  x    k2 k  0,5 1  cos x 
 x    k2 k  2 3
Kết hợp với điều kiện, phương trình đã cho có nghiệm x    k2 , 0,5  x    k2 k  3 2
Câu 2 (2,0 điểm). Xung quanh bờ ao của gia đình bác Nam trồng 20 cây chuối. Do không
còn phù hợp bác muốn thay thế để trồng bưởi, lần đầu bác chặt ngẫu nhiên 4 cây. Tính xác
suất để trong 4 cây bác Nam chặt không có hai cây nào gần nhau.
Số phần tử của không gian mẫu là n() 4  C  4845 20 0,5
Trường hợp 1: Cả 4 cây được chặt ở gần nhau có 20 cách
Trường hợp 2: Trong 4 được chặt có đúng 3 cây gần nhau
- Chặt 3 cây gần nhau có 20 cách 0,5
- Mỗi 3 cây gần nhau có 15 cây không gần 3 cây đó. Vậy trường hợp này có: 20 X 15 = 300 cách
Trường hợp 3: Trong 4 cây được chặt có đúng 2 cây gần nhau:
- Chặt đúng 2 cây ở gần nhau có 20 cách
- Với mỗi 2 cây gần nhau có 16 cây không ở gần hai cây này. Trong 16 cây lại có 15 cặp
cây gần nhau. Chọn hai cây không gần nhau trong 16 cây có: 2 C 15  105 0,5 16
Vậy trường hợp này có: 20.105 = 2100 cách
Trường hợp 4: Trong 4 cây được chặt có đúng hai cặp cây gần nhau
- Chọn một cặp cây gần nhau có 20 cách
- Mỗi cách chọn một cặp cây gần nhau lại có 15 cặp cây gần nhau được chọn từ 16 cây. 20.15
Vậy trường hợp này có  150 cách 2 0,5 Vậy n( )
A  4845  (20  300  2100  150)  2275 2275 455 Suy ra: P( ) A   4845 969 3
Câu 3 (2,0 điểm). Cho n là số nguyên dương thỏa mãn n 1  n C  C
 4(n  2). Tìm hệ số n4 n3 của 5
x trong khai triển nhị thức Niu – tơn của n 2 2  (1 2 )  (1 3 ) n P x x x x .
ĐK: n nguyên dương, ta có n 1  n C  C
 4(n  2) tương đương với n4 n3 (n  4)! (n  3)!
(n  4)(n  3) (n  3)(n 1)   4(n  2)    4 0,5 (n 1)!.3! n!.3! 6 6  3n  15  n  5. Với n  5, ta có 5 2 10
P  x(1 2x)  x (1 3x) 5 Xét khai triển: 5 x(1 2x) k
 xC (2x)k , suy ra hệ số chứa 5x ứng với k  4 và ta 5 k 0 có 4 4 a  C ( 2  )  80 1,0 5 5 10 Xét khai triển: 2 10 2 x (1 3x) k
 x C (3x)m , suy ra hệ số chứa 5x ứng với m  3 và 10 m0 ta có 3 3 a  C .3  3240. 5 10 Vậy hệ số của 5
x trong khai triển là: a  80  3240  3320. 0,5 5 4
Câu 4 (2,0 điểm). Cho dãy số u được xác định bởi: n  1 n 1 n  12n   1 2021nu * u  , u  u  ; n   . Tính lim n 1 n 1 3  n n n  2 1  2  2 n  2 2020   u u 2n 1 n 1  n     n 1 n n  2 1  2  2 n  2     u u 1 1 n 1  n       0,75 n 1 n
 2n  2 n  2 1  2      u 1 u 1 n 1  n     n 1 n  2 1  2 n  2n 2   u 1 Đặt: n * v  
n   . Ta có v  0và v  v , n   1. n n  , 2 n  2 1 n 1  n Suy ra v  0 n 0,75 u 1 n n *       n  0 u , n 2 n  2 n 2 n  2 n  u  n 2 n  2 2021nu  2021n n  2021 Suy ra lim n  lim .   2  2020  2020 n  2  2020 0,5 5 2 1  2 x  2 x  3x  1
Câu 5 (2,0 điểm). Giải bất phương trình  1. 2 1  2 x  x  1 Điều kiện x  0 2   Ta có 2 1 3 2 x  x  1  2 x    3  1   nên 2 1 2 x  x 1  0  2  4 0,5 Do đó bất phương trình 2 2
 1 2 x  2 x  3x 1  1 2 x  x  1 2 2
 x  x  x 1  x  3x 1
Nếu x  0 thì bất phương trình trở thành 1  1 (vô lý) 1 1 0,5
Nếu x  0 thì bất phương trình  1 x  1  x   3 x x 1 Đặt x 
 t với t  2 , bất phương trình trở thành 1 t 1  t  3 x 0,5 13  2 t 1  3  t  4 13 1 13 13  105 13  105 Với t  thì 2 x    4x 12x  4  0   x  4 x 4 8 8 0,5 13  105 13  105
Vậy bất phương trình có nghiệm là  x  8 8 6
Câu 6 (2,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có ( A 5  ;2) . M ( 1  ; 2
 ) là điểm nằm bên trong hình bình hành sao cho  MDC   MBC và MB  MC .
Tìm tọa độ điểm D biết  1 tan DAM  . 2
Gọi E là điểm thứ tư của hình bình hành MABE, dễ thấy MECD cũng là hình bình hành nên  MEC   MDC. 0,5 Mà  MDC   MBC suy ra  MEC  
MBC hay tứ giác BECM nội tiếp.
Suy ra     180o    180o  90o  90o BMC BEC BEC Ta có   
( . . )      90o AMD BEC c c c AMB BEC hay AMD vuông tại M 0,5 DM Vì  1 1 tan DAM    DM  MA. MA 2 2 0,5 Ta có 2 2 2
MA  4 2  MD  2 2  AD  MA  MD  40 . 2 2 2
AD  40 (x  5)  (y  2)  40 Giả sử D( ; x y) ta có    . 2 2 2 MD  8
(x 1)  (y  2)  8 0,5
Giải hệ phương trình trên được hai nghiệm: (3; 4  ), (1;0).
Vậy có hai điểm D thỏa mãn đề bài là: D( 3  ; 4  ), D(1;0). A B M E C D 7
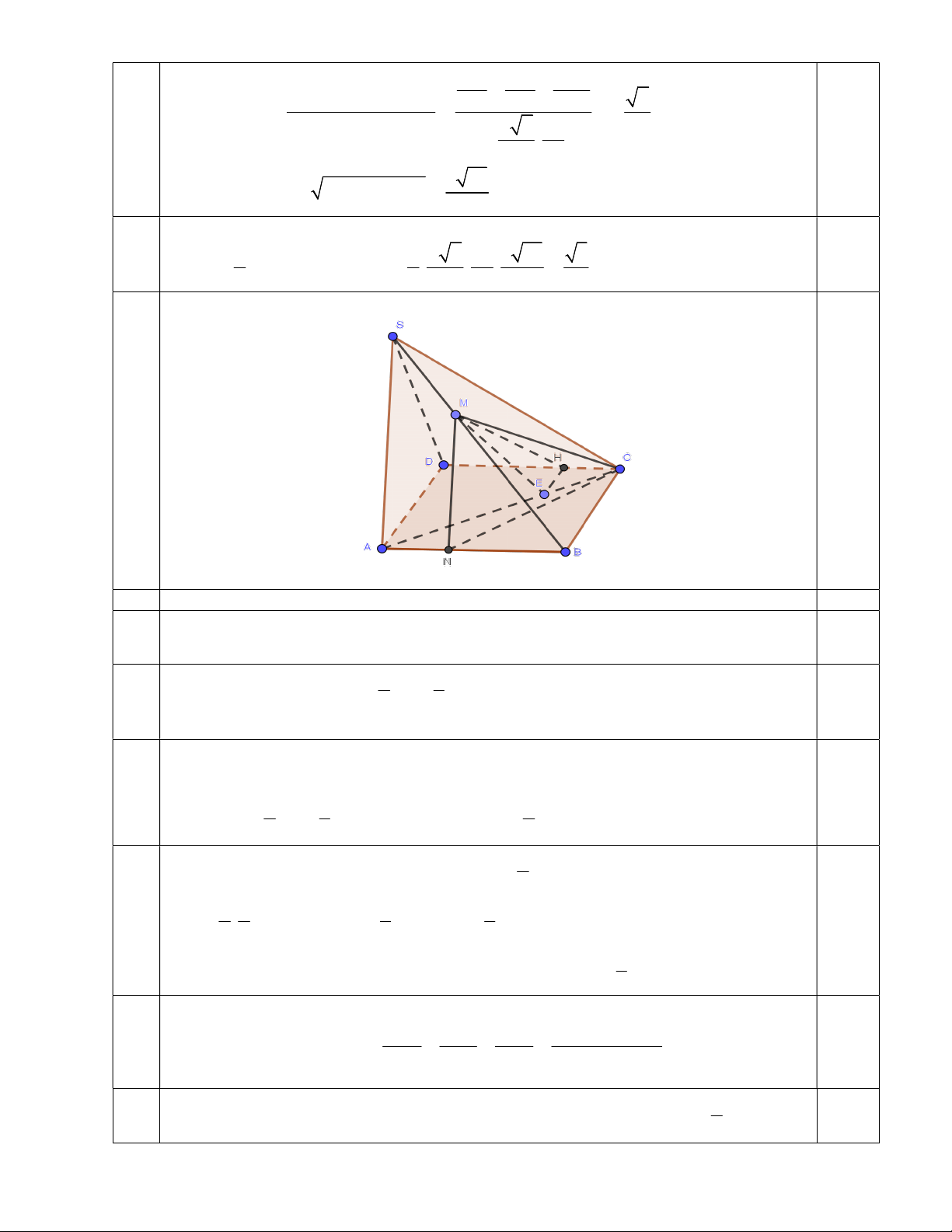
Câu 7 (4,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên  1 
đều bằng a . Gọi M là điểm nằm trên SB sao cho SM  SB . 3
a. Gọi (P) là mặt phẳng chứa CM và song song với S . A Tính theo a diện tích
thiết diện tạo bởi (P) và hình chóp S.ABC . D
b. E là một điểm thay đổi trên cạnh AC . Xác định vị trí điểm E để ME vuông góc với C . D 7a.(2 điểm)
Từ M kẻ MN / /SA (N  AB) . Khẳng định thiết diện là tam giác CMN. 0,5 MN BM 2 2a Ta có:    MN  . SA BS 3 3 2 2 a a 1 7a Xét SMC có: 2 2 2
MC  SM  SC  2.SM .SC.cos MSC = 2  a  2. . . a  9 3 2 9 0,5 a 7  MC  . 3 2 2 2 4a 2 13a CN  BN  CB   a  . 9 3 2 2 2 4a 7a 13a 2 2 2   MN  MC  CN 7 Có 9 9 9 cosCMN     . 2.MC.MN a 7 2a 14 2. . 0,5 3 3 Suy ra 2 3 21 sin CMN  1 cos CMN  . 14
Diện tích thiết diện là: 1 1 a 7 2a 3 21 3 2 0,5 S  .MC.MN.sin CMN  . . .  a (đvdt).  CMN 2 2 3 3 14 6 7b (2,0 điểm)
Đặt CE  xCA . Kẻ EH  CD (H CD)  EH / / AD nên CH  xCD   0,5 Suy ra CH  xCD .
  
 2  1 
MH  CH  CM  xCD  ( CS  CB) 3 3
   0,5 ME  MH  HE
Để ME vuông góc CD điều kiện là:  
    
ME.CD  0  (MH  HE).CD  0  MH.CD  0 do HE  C . D 0,5   2  1   2  2  
 xCD  ( CS  CB) .CD  0  xCD  CS.CD  0  do CB  CD 3 3    3   1 Do SCD đều nên 0 2 CS.CD  CS.C . D cos60  a . Do đó 2 2 2 1 2 2 1 1 .
x a  . a  0  a (x  )  0  x  . 0,5 3 2 3 3 1
Vậy E thuộc đoạn AC thỏa mãn CE  C . A 3 8
Câu 8 (2,0 điểm). Cho a, b, c là độ dài 3 cạnh của một tam giác có chu vi bẳng 1. Tìm giá 2 2 2 4 4 4 a  b  c 1
trị lớn nhất của biểu thức:T     . a  b b  c c  a 2abc  1 
Vì a, b, c là độ dài 3 cạnh của một tam giác có chu vi bẳng 1 nên a,b,c 0;   0,25  2  4 4 4 1 1 1 5a 1 5b 1 5c 1 T          0,5 2 2 2 1 a 1 b 1 c a b c a  a b  b c  c Ta có 2 5a 1 3a 1 2a 1  1   18a  3   0, a   0; 2       2   a  a a  a  2  5a 1  1    18a  3 ,a  0; 0,75 2     a  a  2  5b 1  1  5c 1  1  Tương tự ta có :  18b  3 ,b  0; ,  18c  3 , c   0; 2   2       b  b  2  c  c  2  5a 1 5b 1 5c 1 Suy ra T   
 18 a  b  c  9  9 2 2 2   a  a b  b c  c 0,5 1 1
Dấu đẳng thức xảy ra  a  b  c   T
 9 đạt được  a  b  c  ax 3 m 3
----------------------Hết----------------------