Đề thi HSG Toán 11 năm 2018 – 2019 trường Phùng Khắc Khoan – Hà Nội

Sở giáo dục và đào tạo Hà Nội
Trường Phùng Khắc Khoan
*** ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
Môn : Toán- Khối: 11 Năm học 2018-2019
Thời gian: 150 phút ( Đề có 01 trang)
=============================================== Câu 1 ( 4 điểm)
1 - Tính tổng các nghiệm của phương trình sin x cos x  cos x  sin x  1 trên 0; 2  .
2 - Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3 2
x  x   2 7
2 m  6m x 8  0. Câu 2 ( 6 điểm)
1 - Cho n là số dương thỏa mãn n 1  3 5C  C . n n n 2  nx 1  Tìm số hạng chứa 5
x trong khai triển nhị thức Newton P     .  14 x 
2 - Một tổ gồm 9 em, trong đó có 3 nữ được chia thành 3 nhóm đều nhau. Tính xác xuất để mỗi nhóm có một nữ.
3 - An và Bình thi đấu với nhau một trận bóng bàn có tối đa 5 séc , người nào thắng trước 3 séc sẽ
giành chiến thắng chung cuộc. Xác suất An thắng mỗi séc là 0, 4 (không có hòa). Tính xác suất để An thắng chung cuộc . Câu 3 ( 4 điểm)
1-Trong mặt phẳng tọa độ Oxy , cho các điểm A 2
 ;3, A1;5 và B5; 3  , B7; 2  . Phép quay tâm I  ;
x y biến A thành A và B thành B, tính x  y .
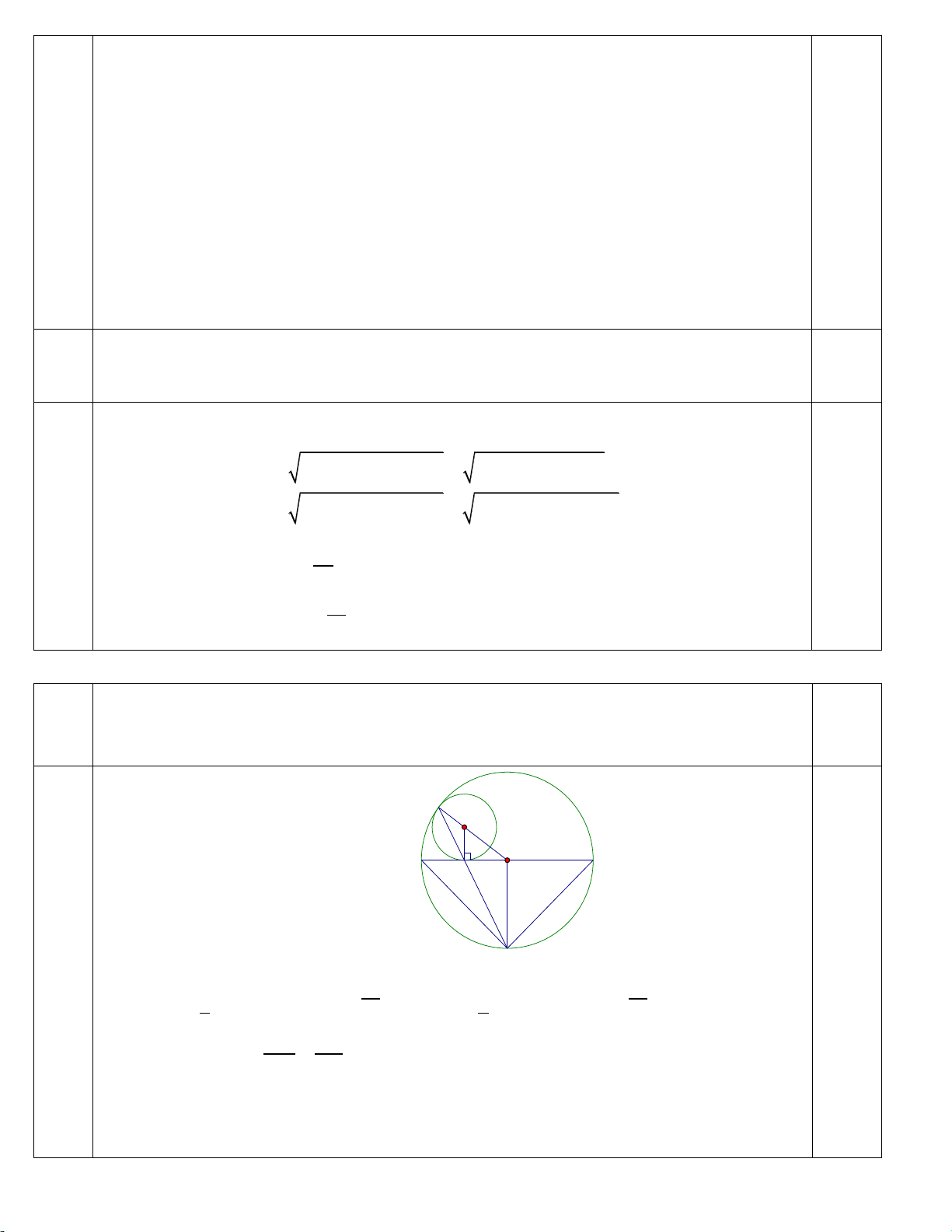
2- Cho đường tròn O; R đường kính AB . Một đường tròn O tiếp xúc với đường tròn O và
đoạn AB lần lượt tại C và D . Đường thẳng CD cắt O; R tại I . Tính độ dài đoạn AI . Câu4 (4điểm)
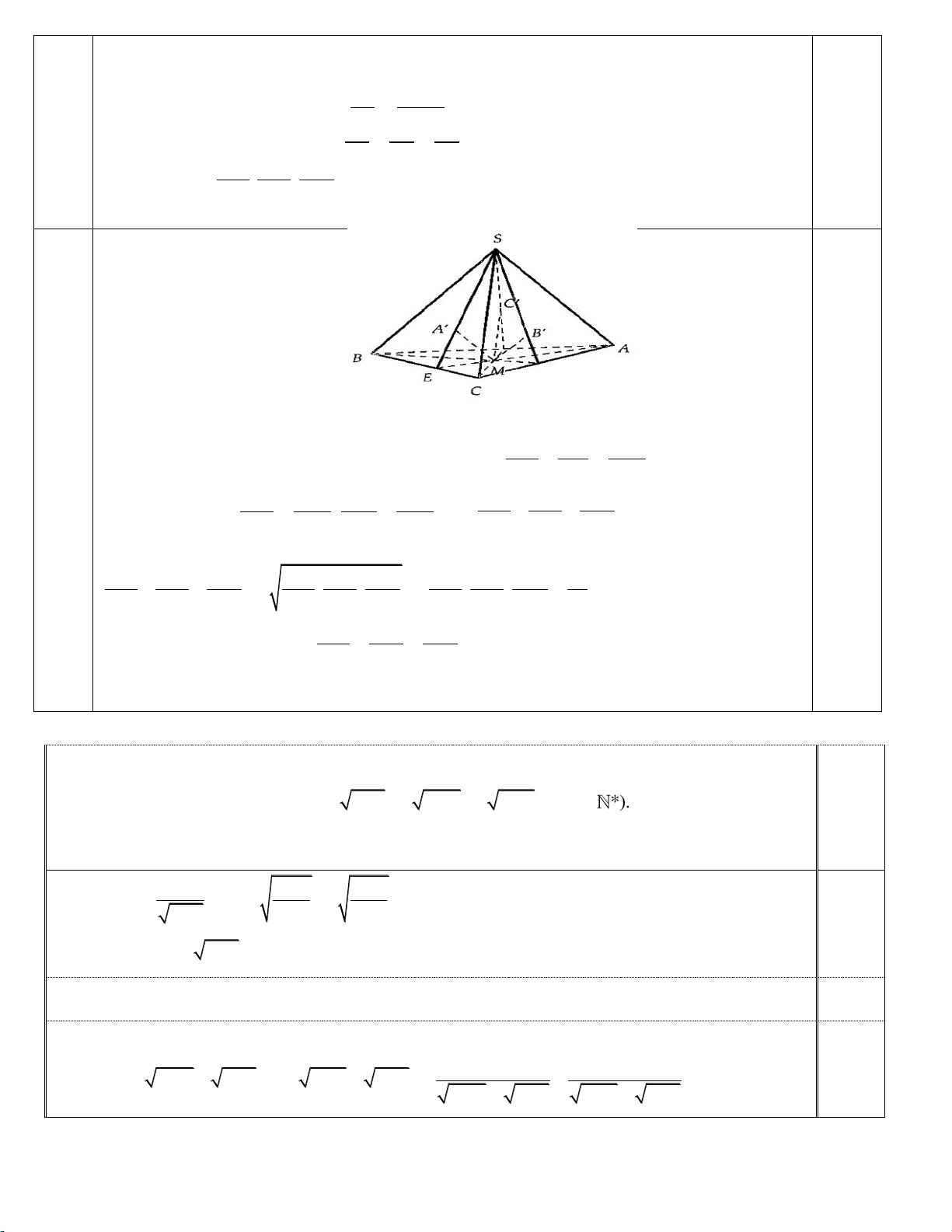
Cho hình chóp S.ABC , M là một điểm nằm trong tam giác ABC . Các đường thẳng qua M song song với S ,
A SB, SC cắt các mặt phẳng SBC,SAC ,SAB lần lượt tại A , B ,C . a) Chứng minh rằng . b) Chứng minh rằng
khi M di động trong tam giác ABC
MA MB MC c)
Tìm vị trí của M trong tam giác ABC để . .
đạt giá trị lớn nhất. SA SB SC
Câu5 (2điểm) Cho a, b, c là ba hằng số và (u ) là dãy số được xác định bởi công thức: n
u  a n 1  b n  2  c n  3 ( n
  *). Chứng minh rằng limu  0 khi và chỉ khi a  b  c  0. n n n
-------------------------------------------HẾT-----------------------------------------
ĐÁP ÁN Thi học sinh giỏi cấp trường MÔN TOÁN LỚP 11 ( 2018- 2019) Câu 1 Nội dung Thang điểm
Tính tổng các nghiệm của phương trình sin x cos x  cos x  sin x  1 trên 0; 2 
sin x cos x  cos x  sin x  1 (3)   
Đặt t  sin x  cos x  2 sin x   t  0; 2.      4  2   t t t 
t  1 2sin x cos x  sin x cos x   3 2 1 1 1 2 2         t 1 t 2t 3 0  2 2 t  3   l 2     2 điểm sin x         4  2 
Với t  1: 2 sin x  1    1,0 4       2 sin x        4  2    x    k2  x  k2 4 4            x  k 2 x   k2  4 4  2       
x     k2
x    k2  4 4  2   
x    k2
x      k2  4 4 1,0  3
Suy ra phương trình có 3 nghiệm trên 0; 2  là x 
; x   ; x  2 2  3 Vậy tổng 3 nghiệm là     3. 2 2
2 - Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3 2
x  x   2 7
2 m  6m x 8  0.
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x , x , x lập thành một 1 2 3 2
cấp số nhân.Theo định lý Vi-ét, ta có x x x  8. 1 2 3
điểm Theo tính chất của cấp số nhân, ta có 2
x x  x . Suy ra ta có 3
x  8  x  2. 1 3 2 2 2
+ Điều kiện đủ: Với m 1 và m  7 thì 2
m  6m  7 nên ta có phương trình 1,0 3 2
x  7x 14x  8  0.
Giải phương trình này, ta được các nghiệm là 1, 2, 4. Hiển nhiên ba nghiệm này lập thành một
cấp số nhân với công bôị q  2. 1,0
Vậy, m 1 và m  7
 là các giá trị cần tìm. Câu
1 - Cho n là số dương thỏa mãn n 1  3 5C  C . n n 2 n 2  nx 1  Tìm số hạng chứa 5
x trong khai triển nhị thức Newton P      14 x 
Điều kiện n  , n  3.  n n n 5. ! ! 5 1 Ta có 1 3 5C  C     n n 1!.n   1 ! 3!.n  3!
n 3 !n 2n   1 6.n  3!
n  7TM  2 2
 n  3n  28  0   n  4   L điểm 1,0 7 2  x 1 
Với n  7 ta có P      2 x   k 1
Số hạng thứ k 1 trong khai triển là k 14 3 T  .C . k x  k 1  7k 7 2
Suy ra 14 3k  5  k  3 1,0 35 Vậy số hạng chứa 5
x trong khai triển là 5 T   x . 4 16
2 - Một tổ gồm 9 em, trong đó có 3 nữ được chia thành 3 nhóm đều nhau. Tính xác xuất để mỗi nhóm có một nữ.
Bước 1: Tìm số phần tử không gian mẫu. 2
Chọn ngẫu nhiên 3 em trong 9 em đưa vào nhóm thứ nhất có số khả năng xảy ra là 3 C 9 điểm
Chọn ngẫu nhiên 3 em trong 6 em đưa vào nhóm thứ hai có số khả năng xảy ra là 3 C . 6
Còn 3 em đưa vào nhóm còn lại thì số khả năng xảy ra là 1 cách. 1,0 Vậy 3 3   C C .1 1680 9 6
Bước 2: Tìm số kết quả thuận lợi cho A .
Phân 3 nữ vào 3 nhóm trên có 3! cách.
Phân 6 nam vào 3 nhóm theo cách như trên có 2 2
C C .1 cách khác nhau. 1,0 6 4 2 2
   3!.C C .1  540. A 6 4 
Bước 3: Xác suất của biến cố A là P  A A 540 27    .  1680 84
3-An và Bình thi đấu với nhau một trận bóng bàn có 5 séc , người nào thắng trước 3 séc sẽ giành
chiến thắng chung cuộc. Xác suất An thắng mỗi séc là 0, 4 (không có hòa). Tính xác suất An thắng chung cuộc
Giả sử số séc trong trân đấu giữa An và Bình là x . Dễ dàng nhận thấy 3  x  5. Ta xét các trường hợp: 2
TH1: Trận đấu có 3 séc  An thắng cả 3 séc. Xác suất thắng trong trường hợp này là: điểm
P  0, 4.0, 4.0, 4  0, 064 1
TH2: Trận đấu có 4 séc  An thua 1 trong 3 séc: 1, 2 hoặc 3 và thắng séc thứ 4 .
Số cách chọn 1 séc để An thua là: 1
C (Chú ý xác xuất để An thua trong 1 séc là 0, 6. ) 3 1,0 1 3
 P  C .0,4 .0,6  0,1152 2 3
TH3: Trận đấu có 5 séc  An thua 2 séc và thắng ở séc thứ 5 .
Số cách chọn 2 trong 4 séc đầu để An thua là 2 C cách. 4 2 3 2
 P  C .0,4 .0,6  0,13824 1,0 3 4
Như vậy xác suất để An thắng chung cuộc là: P  P  P  P  0,31744 1 2 3
1-Trong mặt phẳng tọa độ Oxy , cho các điểm A 2  ;3, ’
A 1;5 và B 5; 3  , ’ B 7; 2  . Phép quay tâm I  ;
x y biến A thành ’
A và B thành ’
B , tính x  y Q
A  A '  IA  IA ' 1 Q
B  B '  IB  IB ' 2 O,     O,         2 1,0    2
  x2  3 y2  1 x2  5 y2 điểm Từ   1 và 2  
 5 x2  3
  y2  7  x2   2   y2   25 x 
6x  4y 13  2      1,0 x  y  3 
4x 12y 19 31 y    2
Cho đường tròn O; R đường kính AB . Một đường tròn O tiếp xúc với đường tròn O
và đoạn AB lần lượt tại C và D . Đường thẳng CD cắt O; R tại I . Tính độ dài đoạn AI . 2 C O' điểm B A D O I R R Ta có: V      V        I  D CD CI 2 R     O O CO CO   1 R C,   R C,   R  R   R  CD CO 1,0 Từ   1 và 2    OI€ O D
  OI  AB  I là điểm chính giữa của cung CD CI AB . 1,0 Câu
Cho hình chóp S.ABC , M là một điểm nằm trong tam giác ABC . Các đường thẳng qua M song 4 song với S ,
A SB, SC cắt các mặt phẳng SBC,SAC,SAB lần lượt tại A , B ,C . a) Chứng minh rằng b) Chứng minh rằng
khi M di động trong tam giác ABC ?
MA MB MC c) . .
nhận giá trị lớn nhất. Khi đó vị trí của M trong tam giác ABC là: SA SB SC 2 điểm a) Do MA S
∥ A nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử E là giao điểm của mặt 0,5 MA ME S
phẳng này với BC . Khi đó ,
A M , E thẳng hàng và ta có: MBC   . SA EA S ABC MB S MC S MA MB MC B / Tương tự ta có: MAC  , MAB  . Vậy  
 1. Vậy đáp án đúng là . SB S SC S SA SB SC ABC ABC 0,5
c) Ap dụng bất đẳng thức Cauchy ta có : MA MB MC
MA MB MC
MA MB MC 1 3    3 . .  . .  SA SB SC SA SB SC SA SB SC 27 . MA MB MC
Dầu bằng xảy ra khi và chỉ khi:    S  S  S . MAC MAB MBC SA SB SC 1,0
Điều này chỉ xảy ra khi M là trọng tâm tam giác ABC . Vậy đáp án đúng là B. Câu5 (2điểm)
Cho a, b, c là ba hằng số và u là dãy số được xác định bởi công thức: n 
u  a n 1  b n  2  c n  3 ( n   *). n
Chứng minh rằng lim u  0 khi và chỉ khi a  b  c  0. n n 2,0 đ   Đặ u n 2 n 3 t n v   a  b  c
 v  a  b  c khi n   n n n 1 n 1 n 1 0, 5 Ta có: u  v n 1 n n 0, 5
cho nên: nếu a  b  c  0 thì lim u ( )   0. n n 0, 5
Ngược lại nếu a  b  c  0  a  b
  c thì khi n   ta có b c u  b n 
 n   c n   n     n     2 2 1 3 1 0
n  2  n 1
n  3  n 1 0,5