Đề thi HSG Toán 11 năm 2020 – 2021 trường THPT Lưu Hoàng – Hà Nội
Đề thi HSG Toán 11 năm 2020 – 2021 trường THPT Lưu Hoàng – Hà Nội gồm 01 trang với 05 câu tự luận, thời gian làm bài 120 phút, đề thi có lời giải chi tiết và hướng dẫn chấm điểm.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT LƯU HOÀNG
NĂM HỌC 2020 – 2021
Môn thi: Toán - Lớp: 11 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút, không kể thời gian giao đề)
Câu 1 (5 điểm). Cho phương trình: cos2x – 2cosx + m = 0 (1), (với m là tham số).
a) Giải phương trình với m = -3.
b) Tìm m để phương trình (1) có nghiệm x thuộc đoạn [0; /2].
Câu 2 (5 điểm). x 2
a) Trong mặt phẳng tọa độ Oxy. Cho hàm số y có đồ thị (C). Viết 2x 3
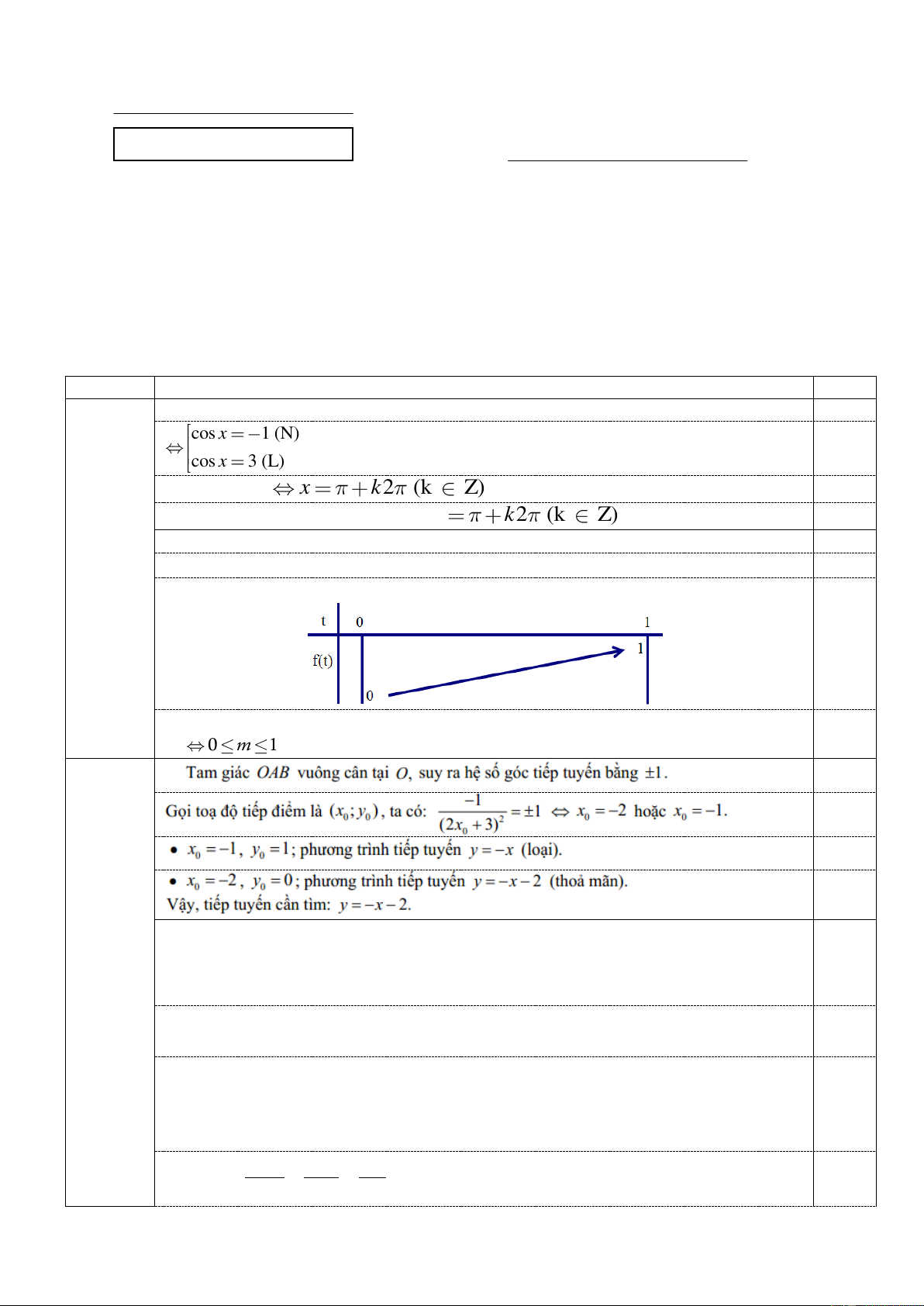
phương trình tiếp tuyến với đồ thị (C), biết tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân.
b) Cho đa giác đều 18 cạnh. Nối tất cả các đỉnh với nhau. Chọn hai tam giác
trong số các tam giác vuông tạo thành từ 3 đỉnh trong 18 đỉnh. Tính xác suất để chọn
được hai tam giác có cùng chu vi.
Câu 3 (5 điểm). u 5 1 n 1
a) Cho dãy số (u ) thỏa mãn: 2 lim n
(n N*) . Tìm . 1 1 u 2 k k u u u n 2 1 2 n n
b) Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty Bảo
Việt với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12
triệu đồng với lãi suất hàng năm không đổi là 6% / năm. Hỏi sau đúng 18 năm kể từ
ngày đóng, người đó thu về được tất cả bao nhiêu triệu đồng (kết quả làm tròn đến hai
chữ số phần thập phân).
Câu 4 (4 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng
SA vuông góc với mặt đáy, góc giữa SB và mặt đáy bằng 0
60 . Gọi N là trung điểm của BC.
a) Tính cosin của góc giữa hai đường thẳng SD và AN.
b) Gọi H, K là hai điểm lần lượt thuộc các đường thẳng SB và DN sao cho HK
SB, HK DN. Tính độ dài đoạn HK theo a.
Câu 5 (1 điểm). Cho x, y R thoả mãn: x2 + y2 = 1. Tìm giá trị lớn nhất, nhỏ nhất của 2 x biểu thức: A = ( 2 6xy) . 2xy 2 2 y 1 ----------HẾT----------
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh: ...................................... Số báo danh: ................
Chữ ký giám thị coi thi số 1:
Chữ ký giám thị coi thi số 2:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI HƯỚNG DẪN CHẤM
TRƯỜNG THPT LƯU HOÀNG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2020 – 2021 ĐÁP ÁN CHÍNH THỨC
Môn thi: Toán - Lớp: 11 I. Hướng dẫn chung
1. Nếu thí sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ điểm từng phần
như hướng dẫn quy định.
2. Việc chi tiết hóa thang điểm (nếu có) so với thang điểm trong hướng dẫn chấm phải đảm bảo
không sai lệch với hướng dẫn chấm và được thống nhất thực hiện trong Ban chấm thi.
3. Thang điểm được tính đến 0,25. Sau khi cộng điểm toàn bài, không làm tròn.
II. Đáp án và thang điểm Câu Đáp án Điểm
a) Với m = -3, phương trình có dạng: cos2x – 2cosx – 3 = 0 0.5 cos x 1 (N) 0.5 cos x 3 (L) Với cosx = -1 x k2 (k Z) . 0.5
Vậy phương trình có họ nghiệm là: x k2 (k Z) 0.5
b) Đặt t = cosx, x [0; /2] t [0; 1]. 0.5 Câu 1
Khi đó phương trình đã cho m = -t2 + 2t, t [0; 1] (*). 0.5
(5 điểm) Xét hàm số: f(t) = -t2 + 2t, t [0; 1]. 1.0
Để phương trình đã cho có nghiệm x [0; /2] phương trình (*) có nghiệm t [0; 1.0 1]
0 m 1. Vậy m [0; 1]. a) 1.0 1.0
(vì qua gốc tọa độ O). 0.5 0.5
a) Gọi A là biến cố: “Chọn hai tam giác trong số các tam giác vuông tạo thành từ 3
đỉnh trong 18 đỉnh”. Giả sử đa giác đều đã cho nội tiếp đường tròn (C). 0.5 Câu 2
Vì tam giác vuông tạo thành từ 3 đỉnh trong 18 đỉnh của đa giác đều nên tam giác (5 điểm)
vuông đó có cạnh huyền là đường chéo của đường tròn (C).
Suy ra số tam giác vuông tạo thành từ 3 đỉnh trong 18 đỉnh của đa giác đều là: 0.5 9.16=144 2 ( n ) C 144
Vì hai tam giác vuông bất kì trong 144 tam giác vuông luôn có cạnh huyền bằng nhau
nên hai tam giác này có cùng chu vi khi và chỉ khi chúng là hai tam giác bằng nhau.
Trong 144 tam giác vuông này chia đều thành 4 nhóm tam giác bằng nhau có chu vi 0.5
của mỗi tam giác ở hai nhóm khác nhau là khác nhau 2 ( n ) A 4C . 36 2 n( ) A 4C 35 36 P( ) A 2 n( ) 0.5 C 143 144 1 a) Ta có: u u u ( 2 u 4 ) 4 n Dãy không giảm. n , 0 1 n n n 2 0.5
Nếu có số M: un M với mọi n, thì tồn tại limun = L. Vì un u1 L u1 1 Khi đó ta có: L =
L2 – L + 2 L = 2. (Vô lý) 2 0.5 limu n = 1 1 Ta có: 2
u 2u 4 2u u (u ) 2 ( 2 u ) 2 n n n 1 n n n 1 u (u ) 2 ( 2 u ) 2 n n n 1 0.5 1 1 1 1 1 1 ( n N *) u 2 u u 2 u u 2 u 2 n n n 1 n n n 1 n 1 1 1 n 1 1 Do đó: lim = 2 0.5 Câu 3 u u u u 1 u k 1 2 2 2 k 1 n 1 k k 1 (5 điểm)
b) Gọi Tn là số tiền vỗn lẫn lãi sau n năm, a là số tiền hàng tháng gửi vào ngân hàng
và r là lãi suất. Ta có: 0.5
- Sau 1 năm, có số tiền là: T a(1 r) 1
- Sau 2 năm, có số tiền là: 2
T T (1 r) a(1 r) a(1 r) a(1 r) 2 1
- Sau 3 năm, có số tiền là: 2 3
T T (1 r) a(1 r) a(1 r) a(1 r) a(1 r) 0.5 3 2 ….
- Sau n năm, có số tiền là: n r 1.0 2
T a(1 r) a(1 r) ... a(1 (1 ) 1 r)n . a (1 r). n r
Sau 18 năm người đó thu được số tiền là: 18 (1 0,06) 1 1.0 T 12.(1 0,06). 393,12 (triệu đồng) 18 0,06 a) Đặt AB , a AD , b AS c với S . a b . b c .
c a 0 và a b a, c a 3 H 0.5 A B K N D C 1
Ta có SD b c và AN a b 0.5 2 2 Câu 4 2 2 2 2 1 a 5 2 1 a Suy ra SD
b c 2a, AN a b và S . D AN b 0.5 (5 điểm) 4 2 2 2 2 a 1 Vậy SD AN 2 cos , 0 . Suy ra SD AN 1 cos , . 0.5 a 5 2 5 2 5 2 . a 2 1
b) + Ta có SB a c và DN a b 0.5 2
HK HB BN NK xSB BN yDN x a c 1 1
b y a b 2 2 0.5 1 y HK HB BN NK x y a b xc 2 2 2 x y 2 2
x ya xc 0 a 3xa 0 HK SB Vì nên y 1 HK DN 2 2 x y 2 2 y 1 a b 0
x y a a 0 4 4 1 0.5 x
4x y 0 16
4x 5y 1 1 y 4 2 3 3 1 3 3 1 a 3 Suy ra HK a b c HK a b c 16 8 16 16 8 16 4 0.5 Vậy a 3 HK . 4
Vì x2 + y2 = 1 suy ra x = sint, y = cost, với t [0; 2]. 0.25 2 2 2(x 6xy) 2(sin t 6sin t.cos t) 6sin 2t cos 2t 1 Khi đó: A = . 0.25 2 2 2xy 2 y 1 2sin t.cos t 2 cos t 1 sin 2t cos 2t 2 Câu 5 Xét phương trình: (1 điểm) 6sin 2t cos 2t 1 A ( A 6)sin 2t ( A 1) cos 2t 1 2 A (*) 0.25 sin 2t cos 2t 2 (*) có nghiệm 2 2 2 2 ( A 6) ( A 1) (1 2 ) A A 3A 18 0 6 A 3
Vậy GTNN, GTLN của A lần lượt là -6 và 3. 0.25