Đề thi HSG Toán 12 cấp tỉnh năm 2020 – 2021 sở GD&ĐT Bà Rịa – Vũng Tàu

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 12 CẤP TỈNH
TỈNH BÀ RỊA - VŨNG TÀU
NĂM HỌC 2020 – 2021
ĐỀ THI CHÍNH THỨC MÔN THI: TOÁN Đề thi gồm 02 trang
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Ngày thi: 08/12/2020 ĐỀ BÀI
Câu 1: Giải phương trình 3 cos 2 .
x sin x + 2cos x = sin x + 2cos x
Câu 2: Tìm hệ số của số hạng chứa 9
x trong khai triển nhị thức Niu-tơn của  1 n 3 x  +  biết rằng 3 x    n 1 + n C − = + + C + n n n 7 3 . 4 3 ( )
Câu 3: Cho hình nón đỉnh S có đường cao SO . Gọi A và B là hai điểm thuộc đường tròn đáy nón
sao cho khoảng cách từ O đến AB bằng a ,  o SAO = 30 và  o
SAB = 60 . Tính diện tích xung quanh của hình nón.
Câu 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng a 2 . Gọi C′ là
trung điểm của SC . Mặt phẳng đi qua AC′ và song song với BD cắt SB tại B′ và cắt SD
tại D′ . Tính thể tích khối chóp S.AB C ′ D ′ ′. 2
Câu 5: Tìm tất cả giá trị thực của tham số m để hàm số
x + 2x − m y =
đồng biến trên khoảng x − m  1 ;  −∞ −  . 2    Câu 6: Cho hàm số 2 3 2
y = x + (m +1)x + ( 2
m + 4m + 3) x với m là tham số thực. Tìm tất cả giá trị của 3
m để hàm số có hai điểm cực trị x , x và biểu thức A = x ⋅ x − 2 x + x đạt giá trị nhỏ nhất 1 2 ( 1 2) 1 2
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với mặt phẳng
(ABCD)và SA = a. Gọi I là trung điểm của .
SD Tính khoảng cách giữa hai đường thẳng SB và CI.
Câu 8: Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , AA′ = a . Hình chiếu của
A đỉnh trên mặt phẳng ( A′B C
′ ′) trùng với trung điểm của A′B′ . Gọi ϕ là góc giữa hai đường
thẳng A′B và AC′. Tính cosϕ . 1 y−2
Câu 9: Cho hai số thực x, y khác 0 , biết: ( 2 + + ) = ( 2 + − ) = ( 2 1 1 + ) 1 x y x x x x y . Tính giá trị
biểu thức = 2x − 2−x − 2 + 2y − 2−y P x − 2y . 2
log x + log 5 − x = log 3x +1 4 2 ( ) 8 ( )3
Câu 10: Giải phương trình Câu 11: Cho hàm số 3 2
y = x − 3x +1 có đồ thị (C), đường thẳng (d ) : y = mx +1 và điểm K (3;10).
Tìm tất cả giá trị thực của tham số m sao cho (C) và (d ) cắt nhau tại ba điểm phân biệt ,
A B,C trong đó A(0; )
1 và trọng tâm của tam giác KBC nằm trên đường thẳng y = 2x + 3. 1
Câu 12: (1,25 điểm). Tìm tất cả giá trị thực của m để hàm số y = (x + ) −(m + ) 2 2ln 1
1 ln(2 − x) − m x đạt
cực tiểu tại điểm x =1. 3  3
x − y = x + y (1)
Câu 13: Giải hệ phương trình  .
y + 3 = x + 2 x (2)
Câu 14: Chọn ngẫu nhiên ba số đôi một khác nhau từ tập hợp {1;2;3; ;
… 100} gồm 100 số nguyên dương
đầu tiên. Tính xác xuất để chọn được ba số là độ dài ba cạnh của một tam giác.
Câu 15: Cho khối lăng trụ ABC.A′B C
′ ′ có AB = AC = a, BC = a 3 . Các đường thẳng BB ,′ BA ,′CA′
cùng tạo với mặt phẳng ( ABC) một góc 60 . Điểm M nằm trên cạnh AA′ . Mặt phẳng (α )
qua M và song song với ( ABC) lần lượt cắt các đoạn thẳng AB ,′ BC ,′CA′ tại các điểm
D, E, F . Biết rằng thể tích khối tứ diện A′DEF bằng 1 3
a , hãy tính tỉ số MA . 18 MA′
Câu 16: Xét 3 số thực dương a,b,c thay đổi. Tìm GTNN của biểu thức 2 2 2 a b c 4 P = + + + . 2 2 2
b + c c + a a + b
a + b + c +1
____________________ HẾT ____________________ 2 HƯỚNG DẪN GIẢI
Câu 1: Giải phương trình 3 cos 2 .
x sin x + 2cos x = sin x + 2cos x . Lời giải 3 cos 2 .
x sin x + 2cos x = sin x + 2cos x ⇔ ( 2 x − ) 3 2cos
1 .sin x + 2cos x = sin x + 2cos x ⇔ ( 2 x − ) 3 2cos
1 .sin x + 2cos x = sin x + 2cos x 2 3 ⇔ 2cos .
x sin x + 2cos x = 2sin x + 2cos x 2
⇔ cos x(sin x + cos x) − (sin x + cos x) = 0 ⇔ ( 2
cos x − )1(sin x + cos x) = 0  π  2 ⇔ 2.sin x + sin x =   0  4    π sin  x  + =  0  π  π x + = kπ x = − + kπ  4   4  ⇔ ⇔ ⇔ 4 (k ∈)  .   sin x = 0 x = kπ x = kπ
Câu 2: Tìm hệ số của số hạng chứa 9
x trong khai triển nhị thức Niu-tơn của  1 n 3 x  +  biết rằng 3 x    n 1 + n C − = + + C + n n n 7 3 . 4 3 ( ) Lời giải ĐK: n ≥ 0. n 1 + n C − = + + C + n n n 7 3 4 3 ( ) (n + 4)! (n +3)! ⇔ ( − = + n + ) 7(n 3) 1 !3! n!3!
⇔ (n + 4)(n + 3)(n + 2) − (n + 3)(n + 2)(n + ) 1 = 42(n + 3) ( n + 3)( 2 2
n + 6n + 8 − n − 3n − 2 − 42) = 0
⇔ (n + 3)(3n − 36) = 0 n = 3 − (ktm) ⇔ n =1  (tm) 12 Khi đó ta có  1 3 x  + 
có số hạng tổng quát là: 3 x     1 k −k T C  =   x = C .x− = + . −k x C . − k k k k k x k 3 ( ) 3( ) 9 12 12 18 3 3 2 2 1 12 12 12  x  Số hạng chứa 9 9
x ⇔ 18 − k = 9 ⇔ k = 2. 2
Vậy hệ số của số hạng chứa 9 x là 9 C . 12 3
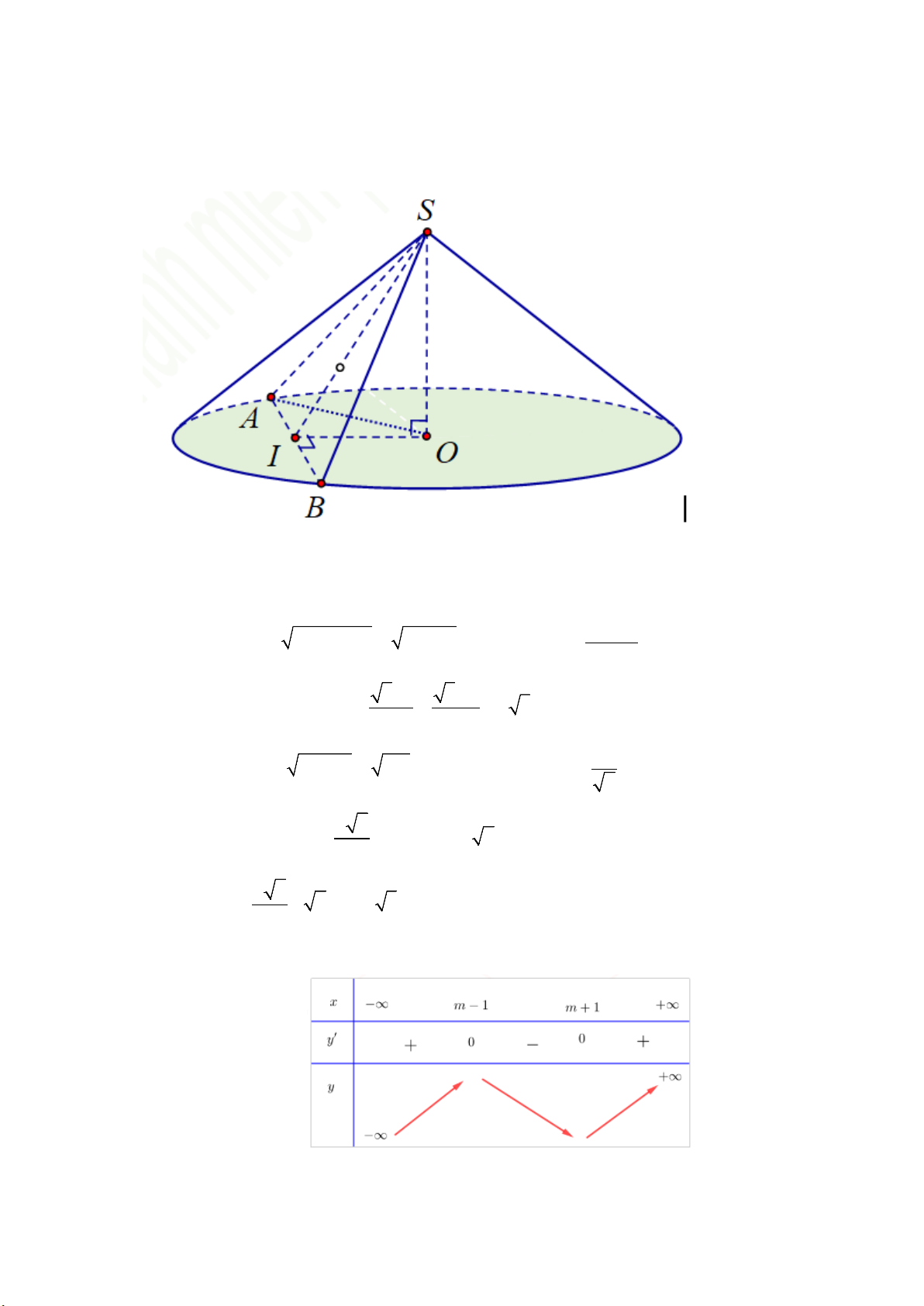
Câu 3: Cho hình nón đỉnh S có đường cao SO . Gọi A và B là hai điểm thuộc đường tròn đáy nón
sao cho khoảng cách từ O đến AB bằng a ,  o SAO = 30 và  o
SAB = 60 . Tính diện tích xung quanh của hình nón. Lời giải
Gọi I là trung điểm của AB . Ta có OK ⊥ (SAB) ⇒ OI = a . Đặt SO = x , Ta có S ∆ OI : 2 2 2 2
SI = SO + OI = a + x (1). S ∆ OA : SO SA = = 2x . o sin 30 3SA 3.2x Xét tam giác đều S ∆ AB : SI = = = x 3 (2). 2 2 Từ (1) và (2) ta có 2 2 2 2 2 2 + = 3 ⇔ + = 3 a a x x a x x ⇔ x = . 2 OA = a o 6 OA = S . O cot 30 =
. SA = 2x = a 2 2 a 6 2 S = π Rl = π a = π a Xq . 2 3 2 Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số tồn tại giá trị nhỏ nhất trên khoảng (0;+ ∞) có hai trường hợp sau: 4
Trường hợp 1: m −1≤ 0 < m +1 ⇔ 1 − < m ≤1. 0 < m −1 Trường hợp 2: 
 f (0) ≥ f (m +1) m >1 ⇔  3 2 2
2020 ≥ (m +1) − 3m(m +1) + 3(m −1)(m +1) + 2020 m > 1 m > 1 ⇔  ⇔ 
⇔ 1< m ≤ 2 . 2
m − m − 2 ≤ 0  1 − ≤ m ≤ 2 Vậy 1 − < m ≤ 2 .
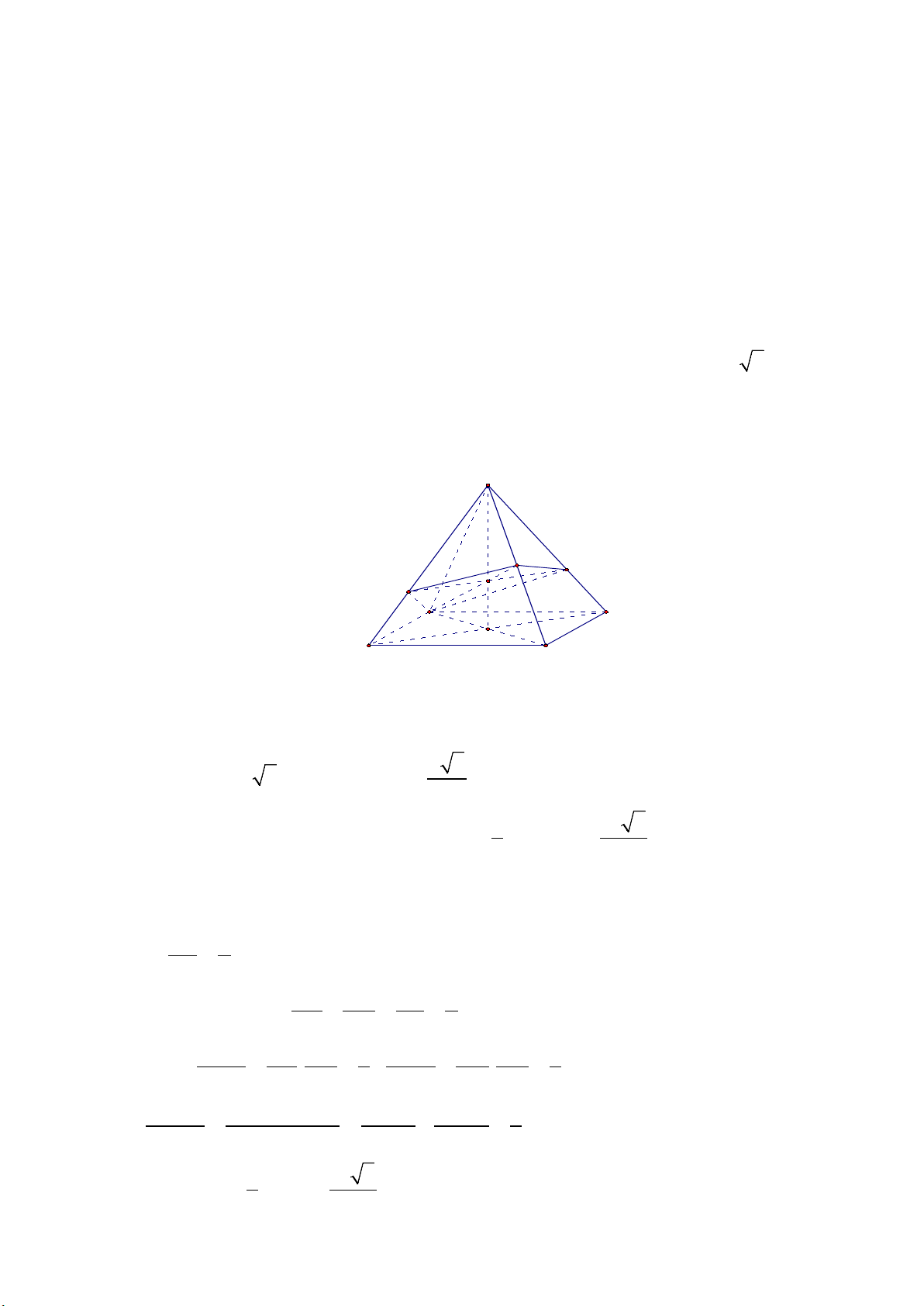
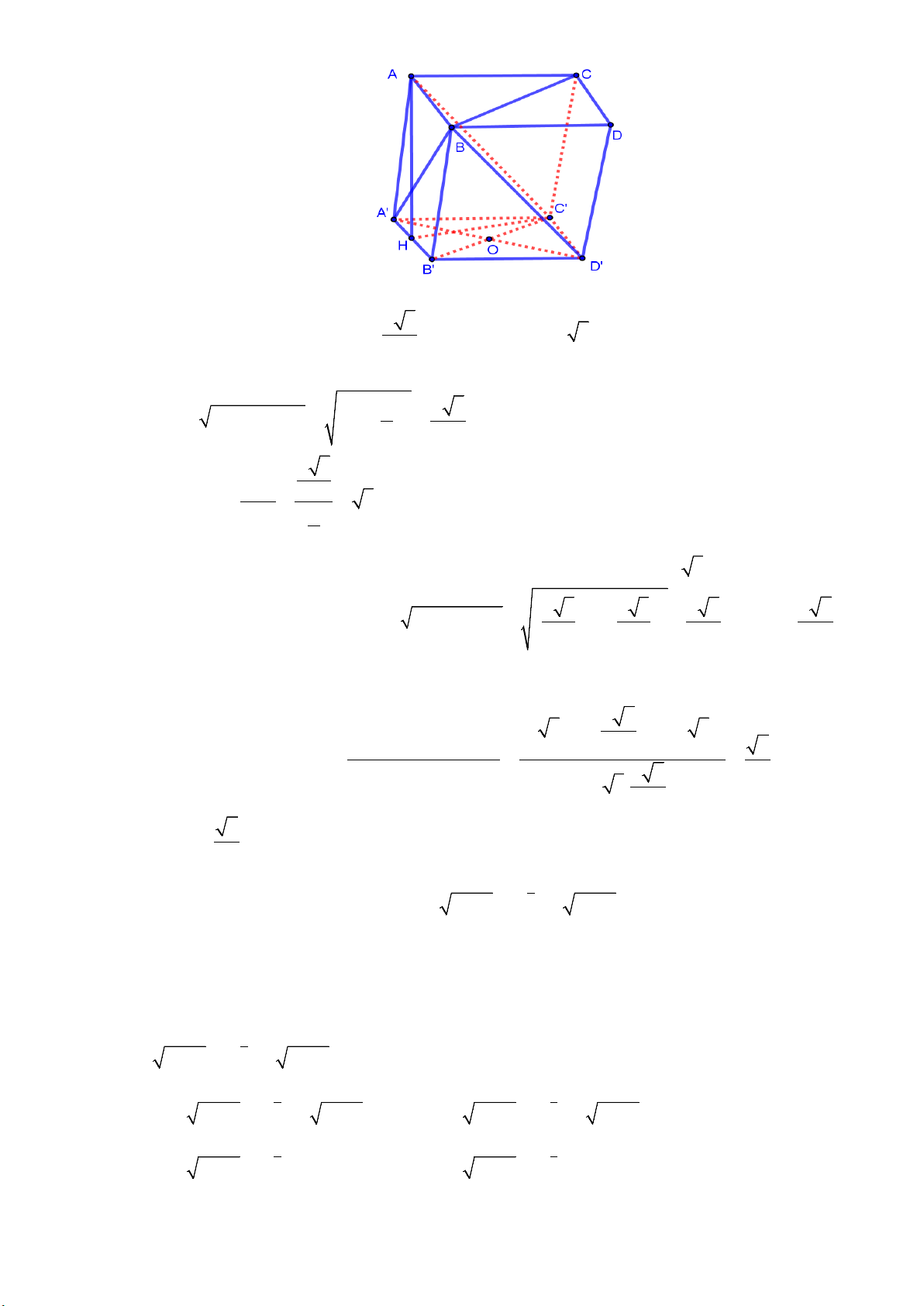
Câu 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng a 2 . Gọi C′ là
trung điểm của SC . Mặt phẳng đi qua AC′ và song song với BD cắt SB tại B′ và cắt SD
tại D′ . Tính thể tích khối chóp S.AB C ′ D ′ ′. Lời giải S C' D' B' I jA D O B C
Gọi O là tâm hình vuông ABCD . Vì S.ABCD hình chóp tứ giác đều nên SO ⊥ ( ABCD) .
Diện tích hình vuông ABCD bằng: 2 S = a ABCD a 6
Ta có AC = a 2 = SA = SC , SO = 2 2 1 a 6
Thể tích khối chóp S.ABCD bằng: V = S SO = S ABCD ABCD. . 3 6
Trong mặt phẳng (SBD) , gọi I = B D
′ ′ ∩ SO , suy ra ,
A I,C′ thẳng hàng
Trong tam giác SAC , ta có AC′ , SO là đường trung tuyến nên I là trọng tâm S ∆ AC . SI 2 ⇒ = SO 3
SB′ SD′ SI 2 Vì B D ′ ′ / /BD nên = = = . SB SD SO 3 V ′ ′ ′ ′ ′ ′ SB SC V ′ ′ SD SC SAB C 1 SAC D 1 Ta có: = . = , = . = V SB SC V SD SC SABC 3 SACD 3 V + ′ ′ ′
V ′ ′ V ′ ′ V ′ ′ V SAB C D SAB C SAC D SAB C SAC D ′ ′ 1 = = + = V V +V V V SABCD SABC SACD 2 SABC 2 SACD 3 3 1 a 6 ⇒ V = = ′ ′ ′ V SAB C D 3 SABCD 18 5 2
Câu 5: Tìm tất cả giá trị thực của tham số m để hàm số
x + 2x − m y =
đồng biến trên khoảng x − m  1 ;  −∞ −  . 2    Lời giải:
Tập xác định D =  \{ } m .
(2x + 2)(x − m) −( 2x + 2x − m) 2
x − 2mx − m y′ = = (x − m)2 (x − m)2 2
Hàm số đồng biến trên khoảng  1 ;  −∞ −
x − 2mx − m  1   ⇔ ≥ 0 x ∀ ∈ ; −∞ − 2    (  x − m)2  2   2 2  1  x  1  x 2mx m 0 x ;  − − ≥ ∀ ∈ −∞ −  m ≥ x ∀ ∈ ; −∞ −   2   ⇔  2x +1  2   ⇔  (*)   1 m∉ ;  −∞ −  1  m ≥ −  2      2 2 2 2x + 2x Xét hàm số ( ) x f x = , có f ′(x) = 2x +1 (2x + )2 1  = f ′(x) x 0 = 0 ⇔  . Ta có bảng biến thiên x =1 m ≥ 1 − ( )  1 * ⇔  1 ⇔ m ≥ − . m ≥ − 2  2 Câu 6: Cho hàm số 2 3 2
y = x + (m +1)x + ( 2
m + 4m + 3) x với m là tham số thực. Tìm tất cả giá trị của 3
m để hàm số có hai điểm cực trị x , x và biểu thức A = x ⋅ x − 2 x + x đạt giá trị nhỏ nhất 1 2 ( 1 2) 1 2 Lời giải Ta có ′ 2
y = x + m + x + ( 2 2 2( 1)
m + 4m + 3). Hàm số có hai điểm cực trị x , x khi và chỉ khi 1 2 phương trình 2
x + m + x + ( 2 2 2( 1)
m + 4m + 3) = 0 có hai nghiệm phân biệt, hay ′ 2 ∆ = m + − ( 2 m + m + ) 2 ( 1) 2 4
3 > 0 ⇔ m + 6m + 5 < 0 ⇔ m∈( 5 − ; 1) − . Theo đinh lý Vi-et 6 + + + + + − A x x
(x + x ) m 4m 3
m 8m 7 (m 4)2 2 2 9 9 − = ⋅ − 2 = − 2⋅(−m −1) = = ≥ . 1 2 1 2 2 2 2 2 Dấu bằng khi m = 4 − thỏa mãn.
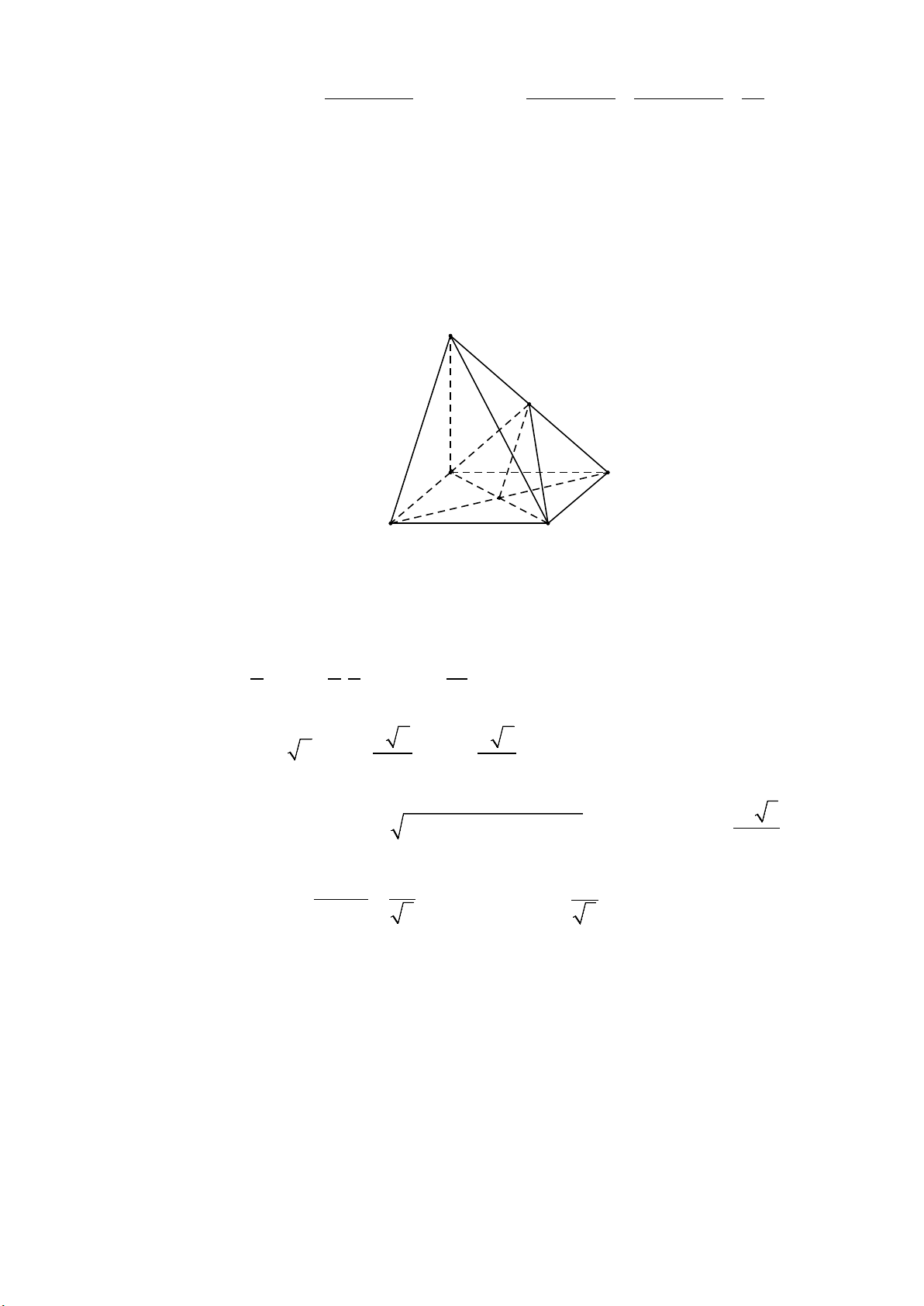
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với mặt phẳng
(ABCD) và SA = a. Gọi I là trung điểm của .
SD Tính khoảng cách giữa hai đường thẳng SB và CI. Lời giải S I A D O B C
Gọi O là tâm của hình vuông ABCD .
Dễ thấy IO || SB ⇒ SB || ( AIC) ⇒ d (SB,CI ) = d (SB,( AIC)) = d (S,( AIC)) . 3 1 1 1 a Ta có V = V = SA S = SACI SACD . . ACD . 2 2 3 12 a 2 a 6
Tính được AC = a 2, IA = , IC = . 2 2 2 a 3
Áp dụng công thức Hê rông S = p( p − a)( p − b)( p − c) tính được S IA ∆ C = 4 3V a a
Do đó d (S,(IAC)) S.IAC = =
. Hay d (SB,CI ) = . S IAC ∆ 3 3
Câu 8: Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a , AA′ = a . Hình chiếu của
A đỉnh trên mặt phẳng ( A′B C
′ ′) trùng với trung điểm của A′B′ . Gọi ϕ là góc giữa hai đường
thẳng A′B và AC′. Tính cosϕ . Lời giải 7
Dựng hình lăng trụ tứ giác ABDC.AB D ′ C
′ ′ , gọi O = A′D′∩ B C ′ ′. Vì A ∆ ′B C ′ ′ đều a 3
⇒ A′O = C H ′ =
⇒ A′D′ = 2A′O = a 3 . 2 Xét A
∆ A′H vuông tại H có 2 +) 2 2 2 a a 3
AH = AA − A H = a   ′ ′ − =  2    2 a 3 AH +)  ′ 2 = = = ⇒  ′ = ° ⇒  tan AA H 3 AA H 60 A′B B ′ =120° . A′H a 2 Xét A ∆ ′B B ′ có 2 2 2 2
A′B = A′B′ + BB′ − 2A′B .′BB′cos120° = 3a ⇒ A′B = a 3 2 2     Xét A
∆ HC′ vuông tại H có 2 2 a 3 a 3 a 6 AC′ a = AH + HC′ = 6   +   =  ⇒ BD′ = . 2   2  2     2
Ta có ϕ = ( A′B AC′)
 = (A′B BD′)  ; ; . 2 (   a )2 a 6 3 +   − (a 3)2 2 2 2
A′B + BD′ − A′D′ 2 Xét A ∆ ′BD′ có    2 cos A′BD′ = = = 2A′ . B BD′ a 6 4 2.a 3. 2 2 ⇒ cosϕ = . 4 1 y−2
Câu 9: Cho hai số thực x, y khác 0 , biết: ( 2 + + ) = ( 2 + − ) = ( 2 1 1 + ) 1 x y x x x x y . Tính giá trị
biểu thức = 2x − 2−x − 2 + 2y − 2−y P x − 2y Lời giải
Gọi D là trung điểm của KC ( y−
x +1 + x)1 = ( x +1− x) 2 2 2 = ( 2 y + ) 1 x y ( y−  − y  x +1 + x 
)1y =( x +1−x) ( x +1+x  )1 2
y = ( x +1+ x)2 2 2 2 2 ⇔  ⇔  ( x  +1 + x  )1 1 2 = ( 2 y + ) 1 x ( 2x +1+x  ) =( 2y +   )1x y y 8  1 2 = 2 − y y − 2y +1 =  0  y  1 ⇔  ⇔  (  + + = + x + + x   )1 x = ( y + ) ( 2x 1 x  )y x y ( 2 2 2 y )1 1 1 y =1 ⇔  2
 x +1 + x = 2x * Xét x − x y − y 2 1 1
P = 2 − 2 − 2x + 2 − 2 − 2y = x +1 + x − − 2x + 2 − − 2 2 x +1 + x 2 2
= x + + x − ( 2x + − x) 1 1 1 − 2x − 2 1 1
= 2x − 2x − = − 2 2 Vậy 1 P = − 2 2
log x + log 5 − x = log 3x +1 4 2 ( ) 8 ( )3
Câu 10: Giải phương trình Lời giải x ≠ 0 x ≠ 0   Điều kiện xác định: 5
 − x > 0 ⇔  1 − < x <   5 3  x +1 > 0  3 Phương trình 2
log x + log 5− x = log 3x +1 4 2 ( ) 8 ( )3 2 3
⇔ log x + log 5 − x = log 3x +1 2 2 2 ( ) 3 ( ) 2
⇔ log x + log 5 − x = log 3x +1 2 2 ( ) 2 ( )
⇔ log x . 5 − x = log 3x +1 2 ( ( )) 2 ( )
⇔ x .(5 − x) = 3x +1 (1) 1
Nếu − < x < 0 thì phương trình (1) có dạng 3
(−x).(5− x) = 3x +1 2
⇔ x −8x −1 = 0 x = 4 − 17 ⇔  . x = 4 + 17 1
Kết hợp với điều kiện − < x < 0 nên x = 4 − 17 . 3
Nếu 0 < x < 5 thì phương trình (1) có dạng
.x(5− x) = 3x +1 2
⇔ x − 2x +1 = 0 ⇔ x =1. Kết hợp với điều kiện 0 < x < 5 nên x =1
Vậy phương trình có tập nghiệm là {4 − 17; } 1 . 9 Câu 11: Cho hàm số 3 2
y = x − 3x +1 có đồ thị (C), đường thẳng (d ) : y = mx +1 và điểm K (3;10). Tìm
tất cả giá trị thực của tham số m sao cho (C) và (d ) cắt nhau tại ba điểm phân biệt , A B,C trong đó A(0; )
1 và trọng tâm của tam giác KBC nằm trên đường thẳng y = 2x + 3. Lời giải x = 0 Xét phương trình 3 2
x − 3x +1 = mx +1 ⇔ x( 2
x − 3x − m) = 0 ⇔  2
x − 3x − m = 0  (*)
Để (C) và (d ) cắt nhau tại ba điểm phân biệt thì (*) có hai nghiệm phân biết khác 0 hay 9  + 4m > 0 9  ⇔ − < m ≠ 0 . m ≠ 0 4 x + x = 3
Gọi các giao điểm của (C) và (d ) là A(0; )
1 , B(x ;mx +1 ,C x ;mx +1 và 1 2 . 1 1 ) ( 2 2 ) x .x = −  m 1 2  + + + +
Gọi G là trọng tâm của tam giác KBC , khi đó x x 3 mx mx 12 1 2 1 2 G ;   hay 3 3    G (2;m + 4) .
Do G ∈(d ) nên m + 4 = 7 ⇔ m = 3 (thỏa mãn)
Câu 12: (1,25 điểm). Tìm tất cả giá trị thực của m để hàm số y = (x + ) −(m + ) 2 2ln 1
1 ln(2 − x) − m x
đạt cực tiểu tại điểm x =1. Lời giải
Tập xác định: D = ( 1; − 2) . Ta có 2 m +1 2 y′ = + − m . x +1 2 − x
Điều kiện cần : Hàm số đạt cực tiểu tại điểm x =1 thì y′( ) 1 = 0 m = 1 − 2 2
⇔ 1+ m +1− m = 0 ⇔ −m + m + 2 = 0 ⇔  . m = 2 Điều kiện đủ : + Với m = 1 − thì 2 2 y − ′ = −1⇒ y′ =
⇒ y′ 1 < 0 . Hàm số đạt cực đại tại điểm x =1. 2 ( ) x +1 (x + ) 1 Vậy m = 1 − không thỏa mãn. + Với m = 2 thì 2 3 2 − 3 5 y′ = + − 4 ⇒ y′ = +
⇒ y′ 1 = > 0 . Hàm số đạt 2 2 ( ) x +1 2 − x (x + ) 1 (2− x) 2
cực tiểu tại điểm x =1. Vậy m = 2 thỏa mãn.
Tóm lại, có duy nhất một giá trị thực của m thỏa mãn đề bài là m = 2 . 3  3
x − y = x + y (1)
Câu 13: Giải hệ phương trình  . Lời giải
y + 3 = x + 2 x (2) 10 + Ta có: 3 3
(1) ⇔ x + x = x + y + x + y + Xét hàm số 3 2
g(t) = t + t; g '(t) = 3t +1> 0 x
∀ ∈ R suy ra hàm số đồng biến trên R 3 3 3 3
(1) ⇔ g(x) = g( x + y) ⇔ x = x + y ⇔ x = x + y ⇒ y = x − x + Thay 3
y = x − x vào (2) ta được 3 6 2
x − 2x − 2 x + 3 = 0 ⇔ a − 2a − 2a + 3 = 0 (a = x ≥ 0) + Xét hàm số 6 2
f (a) = a − 2a − 2a + 3 (a ≥ 0) a =1 5
f '(a) = 6a − 4a − 2; f '(a) = 0 ⇔  4 3 2
6a + 6a + 6a + 6a + 2 = 0(vn) BBT: Căn cứ BBT ta thấy pt 6 2
a − 2a − 2a + 3 = 0 có duy nhất 1 nghiệm là a =1⇒ x =1⇒ y = 0
Vậy hệ có nghiệm duy nhất là (1;0).
Câu 14: Chọn ngẫu nhiên ba số đôi một khác nhau từ tập hợp {1;2;3;…;100} gồm 100 số nguyên dương
đầu tiên. Tính xác xuất để chọn được ba số là độ dài ba cạnh của một tam giác. Lời giải
Ta xét bài toán tổng quát X = {1;2;3;4......; } n .
Không mất tính tổng quát giả sử ba số được chọn là a,b,c với a > b > c ≥1. Trường hợp 1:
Khi n là số lẻ (n = 2m +1)
1) Khi a chẵn (a = 2i với i từ 2 đến m ) Với b = i + k(k từ 1 đển i −1) thì c chạy từ i − k +1 đến i + k −1 m i 1 − m − −
(có 2k −1 cách chọn c
m(m 1)(2m 1) ) ⇒ có 2
s = ∑∑(2k −1) = ∑(i −1) = cách 1 i=2 k 1 = i=2 6
2) Khi a lẻ (a = 2i +1 với i từ 2 đến m ) Với b = i + k(k từ 2 đền i ) thì c chạy từ i − k + 2 đền i + k −1 m i m − +
(có 2k − 2 cách chọn c ) ⇒ có 2
m(m 1)(m 1)
s = ∑∑(2k − 2) = ∑ A = cách 2 i i=2 k=2 i=2 3 Vậy trường hợp 1 có:
m(m 1)(4m 1) s s s − + = + = cách. 1 2 6
1) Khi a chẳn (a = 2i với i từ 2 đền m ) Với b = i + k(k từ 1 đến i −1) thì c chay từ i − k +1 m i 1 − m − −
đến i + k −1 (có 2k −1 cách chọn c ) ⇒ có 2
m(m 1)(2m 1)
t = ∑∑(2k −1) = ∑(i −1) = 1 i=2 k 1 = i=2 6 cách 11
2) Khi a lẻ (a = 2i +1 với i từ 2 đến m −1) Với b = i + k(k từ 2 đến i ) thì c chay từ i − k + 2 m 1 − i m 1 − − −
đến i + k −1 (có 2k − 2 cách chọn c ) ⇒ có 2
m(m 1)(m 2)
t = ∑∑(2k − 2) = ∑ A = 2 i i=2 k=2 i=2 3 cách. Vậy TH 2 có:
m(m 1)(4m 5) t t t − − = + = cách. 1 2 6 − +
Xác suất cần tìm nếu n lẻ s (m 1)(4m 1) 1 3m (n = 2m +1) là = = − . 3 2 C + − − + m m m m 2(2 1)(2 1) 2 8 2 2 1 −
Xác suất cần tìm nếu n chẵn t 4m 5 1 3 (n = 2m) là = = − . 3 C m − m − m 8 4 2 8 4 2
Áp dụng vào bài: Với n = 2m =100 thì xác suất cần tìm là 1 3 65 − = . 2 8.50 − 4 132
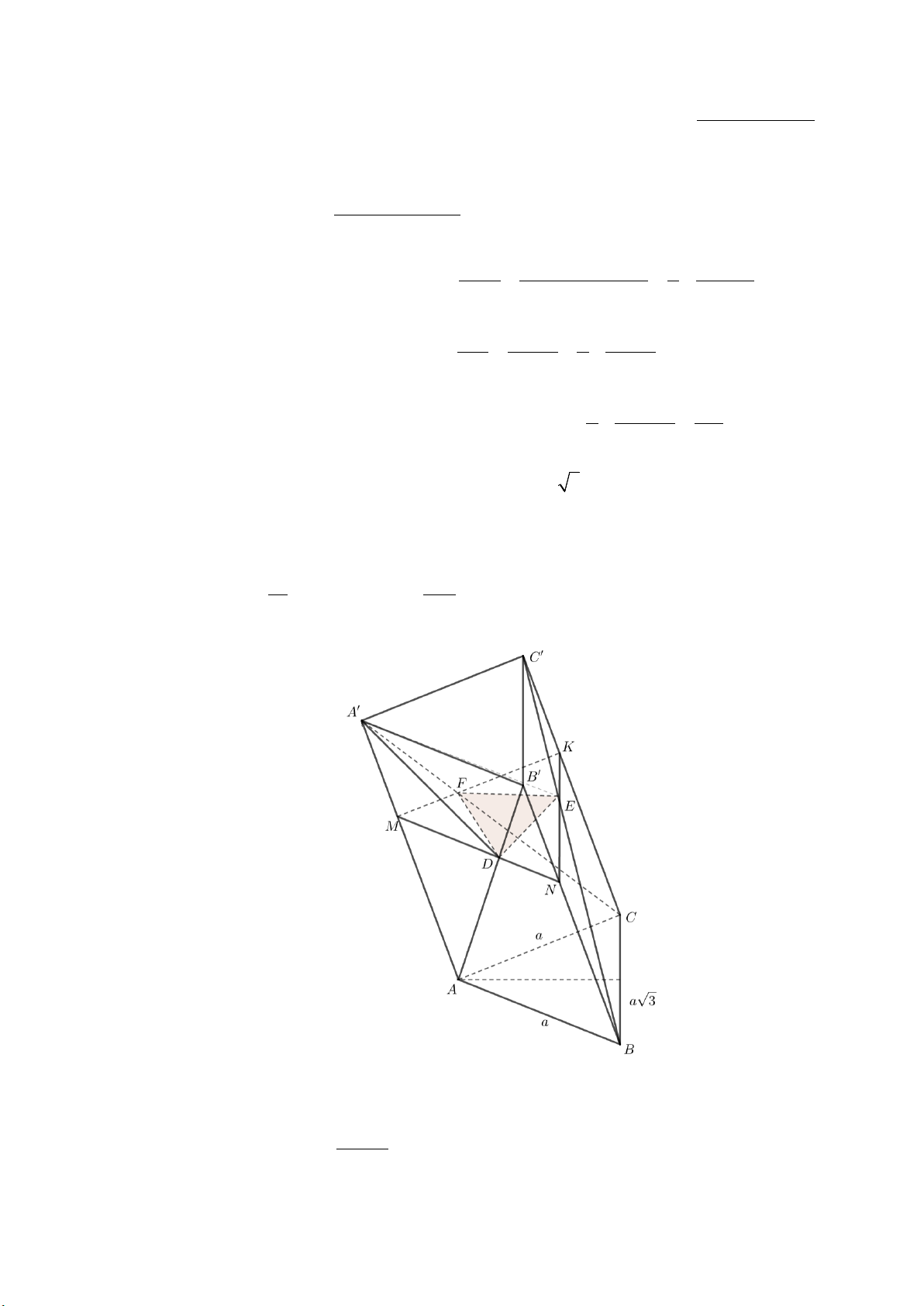
Câu 15: Cho khối lăng trụ ABC.A′B C
′ ′ có AB = AC = a, BC = a 3 . Các đường thẳng BB ,′ BA ,′CA′
cùng tạo với mặt phẳng ( ABC) một góc 60 . Điểm M nằm trên cạnh AA′ . Mặt phẳng (α ) qua M và
song song với ( ABC) lần lượt cắt các đoạn thẳng AB ,′ BC ,′CA′ tại các điểm D, E, F . Biết rằng thể tích
khối tứ diện A′DEF bằng 1 3
a , hãy tính tỉ số MA . 18 MA′
Gọi h là chiều cao của lăng trụ. h
Suy ra BB′ = BA′ = CA′ = sin 60
⇒ AA′ = BB′ = BA′ = CA′ 12
Xét tứ diện A .′ABC có BB′ = BA′ = CA′ nên chân đường cao trùng với tâm đường tròn ngoại tiếp tam giác ABC Suy ra  a 3 h = . R tan 60 = . 3 = a 3 2sin120
Gọi h′ = d (( ABC),(MDF )) suy ra h' AM MD MF ′ = = ⇒ = 1 h − h AA′ MN MK h S ′  ′   ′  ′  ∆ h h h h MDF ⇒ = 1− ⇒ S = − = − −   ∆ S∆ S∆ S EDF MNK 3 MDF MN ∆ K 1 3 1 S  ∆ h  h   h  h MNK  Ta có 1 1 3 1 V = ′ ⇒ = ′ ′ h S∆ a h S A DEF . DEF . . 3 18 3 DE ∆ F 1  ′   ′ 3 1  ⇒ = .′
. .sin120 .1−3 h 1 h a h a a − 6 2  h h    2 3 2 ′ ′ ⇔
= ′ − 3 h + 3 h a h 2 3 3 h h 2 3 2 2 3 ⇔
a = 3a h′ − 3 3ah′ + 3h′ 3 2 3a h′ 2 MA ⇒ h′ = ⇒ = ⇒ = 2 3 h 3 MA′
Câu 16: Xét 3 số thực dương a,b,c thay đổi. Tìm GTNN của biểu thức 2 2 2 a b c 4 P = + + + . 2 2 2
b + c c + a a + b
a + b + c +1 Lời giải ( 2 2 2
a b + b c + c a) ≤ a + b + c ( 2 2 2
a + b + c ) 2 3 ( )
⇔ ∑a(a −b) ≥ 0. ( 2 2 2
a c + b a + c b) ≤ a + b + c ( 2 2 2 3 (
) a + b + c ) 2 2
⇒ ∑a b + c ≤ a + b + c ( 2 2 2
a + b + c ) 2 ( ) ( ) ≤ ( 2 2 2
a + b + c ) 3( 2 2 2
a + b + c ) 3 3 2 4 a 4 a 4 P = ∑ + = ∑ + . 2 2 2 2 2 2 2 b + c
a + b + c +1 a (b + c)
a + b + c +1 2 Caucly-Schwarz 4 t 4 7 ≥ + ≥ +
= f (t) ≥ f (3) = . 2 2 2 2
≥ a (b + c) 2
a + b + c +1 t +1 2 t 3t 3
____________________ HẾT ____________________ 13
Document Outline