Đề thi HSG Toán 12 cấp trường năm 2021 – 2022 trường chuyên Nguyễn Trãi – Hải Dương

SỞ GD-ĐT HẢI DƯƠNG
ĐỀ THI HỌC SINH GIỎI LỚP 12 CẤP TRƯỜNG
Trường THPT chuyên Nguyễn Trãi NĂM HỌC 2021-2022
Thời gian làm bài: 180 phút Môn: Toán Câu 1. (2 điểm) u  Cho dãy số  3 u
xác định bởi u  0,u  n n  1 . 1 n 1    n n 1  5  n u
a) Chứng minh rằng dãy u
có giới hạn hữu hạn và tìm giới hạn đó. n n 1  T b) Đặt 1 T   n . Tìm lim n . n u n n  k   3 1 k 5 4
Câu 2. (2 điểm) Tìm tất cả các hàm số f : ¡  ¡ sao cho:
f  y  f  x  f  2018 x
 y  2017yf (x), x, y¡ . Câu 3. (2 điểm)
Có bao nhiêu cách lát kín bảng 2  2022 bởi các viên domino 1 2 và 2 1 ? Câu 4. (2 điểm)
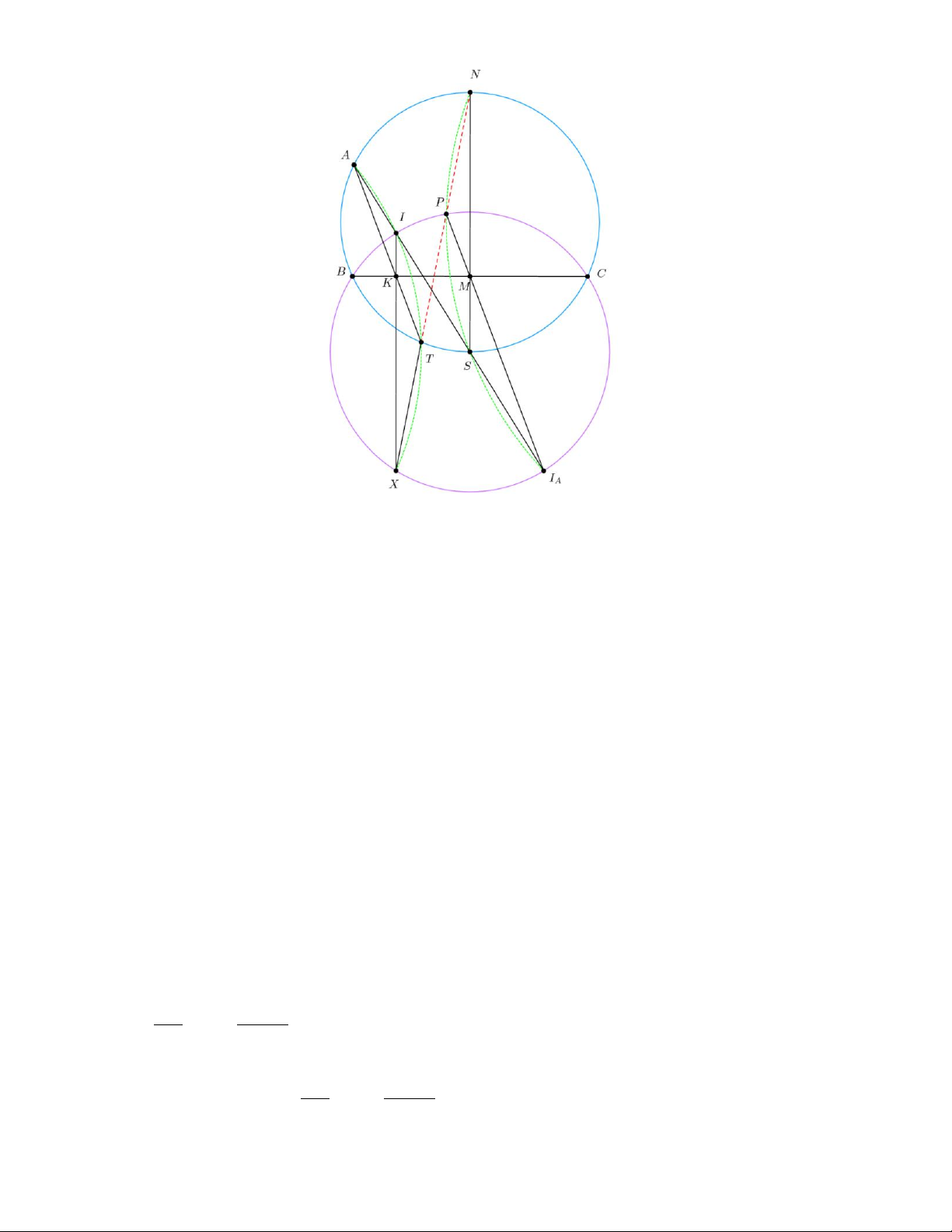
Cho tam giác nhọn ABC với AB  BC . Cho I là tâm nội tiếp của tam giác ABC và  là đường
tròn ngoại tiếp tam giác ABC . Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại K . Đường
thẳng AK cắt  tại điểm thứ hai T . Cho M là trung điểm của BC và N là điểm chính giữa cung »
BC chứa A của  . Đoạn thẳng NT cắt đường tròn ngoại tiếp tam giác BIC ở P . Chứng minh rằng
a) Cho KI cắt (BIC) tại điểm thứ hai X thì N;T; X thẳng hàng. b) PM ‖ AK . Câu 5. (2 điểm) Cho dãy số x  . a x n  ¥ ; *
x  ¥ ; a là nghiệm dương của phương trình 2
x  kx 1  0 ( n 1   n o
k ¥ ; k 1) với số nguyên dương k cho trước.
Khi đó chứng minh rằng x
 x 1 (mod k) . n 1  n 1  Giải Câu 1 :
a) Ta chứng minh bằng quy nạp theo *
n  ¥ , dãy un 
bị chặn trên bởi 1 và là một dãy tăng. n 1  x  * +) Ta có u  1. u  n  ¥ . f x  1 Giả sử 1 n Vì hàm  
3 là đồng biến trên khoảng 5  x ( ;
 1) nên u 1 u
 f u  f 1 1. n n 1   n   
Vậy u  1 với mọi * n  ¥ . n 3 +) Ta có u 
 u . Giả sử u  u n  2 . u ,u 1 n n 1    2 1 Do 1   n n
và f là đồng biến trên khoảng 5 ( ;  1) nên u  f u  f u  u . n 1   n
 n 1 n Vậy dãy un 
tăng và bị chặn trên nên có giới hạn hữu hạn. n 1  a  3 a 1
+) Đặt lim u  a a  a   . n  1 . Suy ra  n 5  a a  3 Vậy lim u  1.  n n 4(u  3) 1 1  2 k   b) Ta có 1 u  3    1 k k    2. 5  u u  3 4 u  3 k 1  k  k 1   1 n 1 1  1  n 1  T   n n    2   1   u  3 k  u  3 3 4 u k  k  3 1 2 2 k 1   1  1 1  1    n  T  .  n  12 4 2 u  3  n  1  1 1 T 1  Suy ra T   n   lim n  . n 6 2 u  3
n 5n  4 10 n Câu 2 :
Giả sử hàm số f (x) thỏa mãn yêu cầu bài toán.
+)Trong (1) thay y bởi f (x) ta có :
f    f  2018 x  f x  2 0
( )  2017( f (x)) ,x  ¡ (2).
+)Trong (1) thay y bởi 2018 x ta có : f  2018 x
 f x  f   2018 ( ) 0  2017x
f (x),x  ¡ (3).
Từ (2) và (3) suy ra f  x 2018
( f (x)  x )  0,x  ¡ (4).
Vậy nếu có x sao cho f (x )  0 thì 2018
f (x )  x
. Vậy f 0  0. 0 0 0 0
Dễ thấy có hai hàm số f (x)  0 và 2018
f (x)  x
,x ¡ thỏa mãn (4). 1 2
+) Ta chứng minh nếu có hàm số f (x) khác hai hàm số f ( x) và f ( x) mà thỏa mãn cả (1) và 1 2 (4) thì vô lý.
Vì f (x) khác f ( x) nên x  ¡ : f (x )  0. Vậy 2018
f (x )  x . 1 1 1 1 1
Vì f (x) thỏa mãn (4) và khác f ( x) nên x  ¡ : x  0; f (x )  0. 2 2 2 2
+) Trong (1) cho x  0  f ( y)  f ( y),y  ¡ .
Không mất tổng quát, giả sử x  0 2
+)Trong (1) thay x bởi x và y bởi ( x ) ta có : 2 1 2018
f (x )  f (x  x ) 1 2 1 2018  x
 f (x )  f (x ) 1 1 1 2018 2018 2018 2018  f (x
 x )  (x  x )  x . 2 1 2 1 1 (vô lý).
+) Bằng cách thử trực tiếp vào (1) ta có kết quả hàm số cần tìm là f (x)  0,x  ¡ . Câu 3: Gọi ( a )
n là số cách lát.
Ta xét hai trường hợp sau:
+) Nếu hàng 2 ô đầu tiên được lát bởi viên gạch 21 thì bảng trên trở thành 2(n 1) ; ta có
a(n 1) cách lát.
+) Nếu 4 ô vuông 2 2 ở 2 hàng đầu tiên được lát bởi 2 viên gạch 1 2 thì ta có ( a ) n cách lát. Như vậy ( a ) n  ( a n 1)  ( a n  2) với ( a 1) 1; ( a 2)  2 .
Suy ra a(n)  F là số Fibonacci thứ n . n
Như vậy số cách lát là F 2022 Câu 4: »
a) Cho AI cắt (ABC) tại điểm thứ hai S , như vậy S là trung điểm cung BC không chứa A .
Theo tính chất trục đẳng phương thì AITX là tứ giác nội tiếp, từ đó: ( AITX ) 0 0 A  TN  A  SN  S
 IX 180  X
 IA  180  X  TA
Và suy ra N;T; X thẳng hàng
b) Đặt P là I M  (BIC) , với I  AI  ( ABC) là tâm đường tròn bàng tiếp góc A . Theo A A
tính chất trục đẳng phương NPSI là tứ giác nội tiếp. Khi đó A T  NS  T  AS  T  XI  P  XI  P  I S  P  NS A
Và từ đó suy ra N; ;
P T thẳng hàng. Như vậy, P  NT  (BIC). Suy ra P  I S  P  NS  T  AI A A
và PM ‖ AK (đpcm). Câu 5: +) Ta có x  . a x  x 1 n 1  n n 1    x x 1 n 1  n 1  x   . n a a x x 1
+) Do a là số vô tỉ nên n 1  n 1  x   n a a   x  +) n 1   x 1 n     ¥ (1) n  a   x  1 +) n 1     1 n  ¥ (2)  a  a +) Ta có   1  x  . a x  x  k n 1 
 n  n     a   x   x  n   x . n k 
 x .k  x .k  x 1  n    n n n 1   a   a  Như vậy x
 k.x  x 1 n 1  n n 1  Suy ra x
 x 1 (mod k) (đpcm). n 1  n 1 